Sammon Mapping

Introduction

Sammon Mapping is a non-linear dimensionality reduction technique introduced by John W. Sammon in 1969. It's particularly effective for visualizing high-dimensional data in two or three dimensions, thus making it easier to identify patterns, clusters, and intrinsic data structures that would be difficult to discern in the original high-dimensional space. The primary goal of Sammon Mapping is to preserve the pairwise distances between points in the high-dimensional space when they are projected into the lower-dimensional space, prioritizing the preservation of structure over mere data reduction.

Background and Theory

Mathematical Foundations

The Sammon Mapping algorithm minimizes a cost function known as the Sammon stress or Sammon's error, which measures the discrepancy between the distances in the original high-dimensional space and the distances in the reduced space. Given a set of $N$ points in a high-dimensional space, let $d_{ij}$ be the Euclidean distance between points $i$ and $j$ in the original space, and $d'_{ij}$ be the distance between the same points in the reduced space. The Sammon stress is defined as:

This error function prioritizes the accurate mapping of smaller distances by weighting the error term by the inverse of the original distances. The goal of the optimization process is to find a configuration of points in the lower-dimensional space that minimizes this error function.

Optimization

The minimization of the Sammon stress is typically achieved through iterative gradient descent methods, starting from an initial configuration (often generated randomly or through another dimensionality reduction technique like PCA). The gradient of $E$ with respect to the coordinates of the points in the reduced space is computed at each step, and the points are moved in the direction that reduces the Sammon stress.

Gradient Calculation

The update step in the gradient descent process requires the calculation of the gradient of the Sammon stress with respect to the coordinates of the points in the reduced space. Let's denote the coordinates of point $i$ in the reduced space as $\mathbf{x}_i$. The partial derivative of $E$ with respect to $\mathbf{x}_i$ is given by:

This derivative can be interpreted as the force exerted on point $i$ by all other points, aiming to correct the discrepancy between the high-dimensional and reduced-space distances.

Step Size and Convergence

The step size in each iteration of the gradient descent process is a crucial parameter affecting the convergence and quality of the final mapping. A fixed step size can lead to oscillations or slow convergence, whereas an adaptive step size, such as one determined by line search methods, can improve convergence speed and stability.

Sammon's Mapping with Non-Euclidean Distances

Although Sammon's Mapping is typically described using Euclidean distances, it can be extended to incorporate other types of distances or dissimilarities, including geodesic distances on manifolds, Mahalanobis distance for data with covariance structure, or even arbitrary dissimilarity measures not derived from a metric space. The choice of distance measure can significantly affect the resulting visualization and the insights that can be drawn from it.

Procedural Steps

1. Initialization: Start with an initial mapping of the high-dimensional data points into the lower-dimensional space. This can be done randomly or based on the output of another dimensionality reduction technique.
2. Distance Computation: Calculate the pairwise distances $d_{ij}$ between points in the original high-dimensional space and the corresponding distances $d'_{ij}$ in the reduced space.
3. Error Calculation: Compute the Sammon stress $E$ using the formula provided above.
4. Gradient Descent: Update the positions of the points in the reduced space by moving them in the direction opposite to the gradient of the Sammon stress. The size of the step taken in each iteration can be controlled by a learning rate parameter.
5. Iteration: Repeat steps 2 to 4 until the Sammon stress converges to a minimum value or until a predetermined number of iterations have been completed.
6. Projection: The final positions of the points in the reduced space represent the Sammon mapping of the original high-dimensional data.

Implementation

Parameters

• n_components: int
  Dimensionality of low-space
  
• max_iter: int, default = 100
  Number of iteration
  
• max_halves: int, default = 20
  Number of halving of step-size
  
• tol: float, default = 0.00001
  Threshold for early-stopping
  
• initialize: Literal['pca'] None, default = ‘pca’
  Methodology for embedding-space initialization
  

Examples

from luma.reduction.manifold import SammonMapping

from sklearn.datasets import make_swiss_roll
import matplotlib.pyplot as plt

X, y = make_swiss_roll(n_samples=500, noise=0.3)

model = SammonMapping(
    n_components=2, max_iter=100, max_halves=35, initialize="pca"
)
Z = model.fit_transform(X)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1, projection="3d")
ax2 = fig.add_subplot(1, 2, 2)

ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=y, cmap="rainbow")
ax1.set_xlabel(r"$x$")
ax1.set_ylabel(r"$y$")
ax1.set_zlabel(r"$z$")
ax1.set_title("Original S-Curve")

ax2.scatter(Z[:, 0], Z[:, 1], c=y, cmap="rainbow")
ax2.set_xlabel(r"$z_1$")
ax2.set_ylabel(r"$z_2$")
ax2.set_title(f"After {type(model).__name__}")
ax2.grid(alpha=0.2)

plt.tight_layout()
plt.show()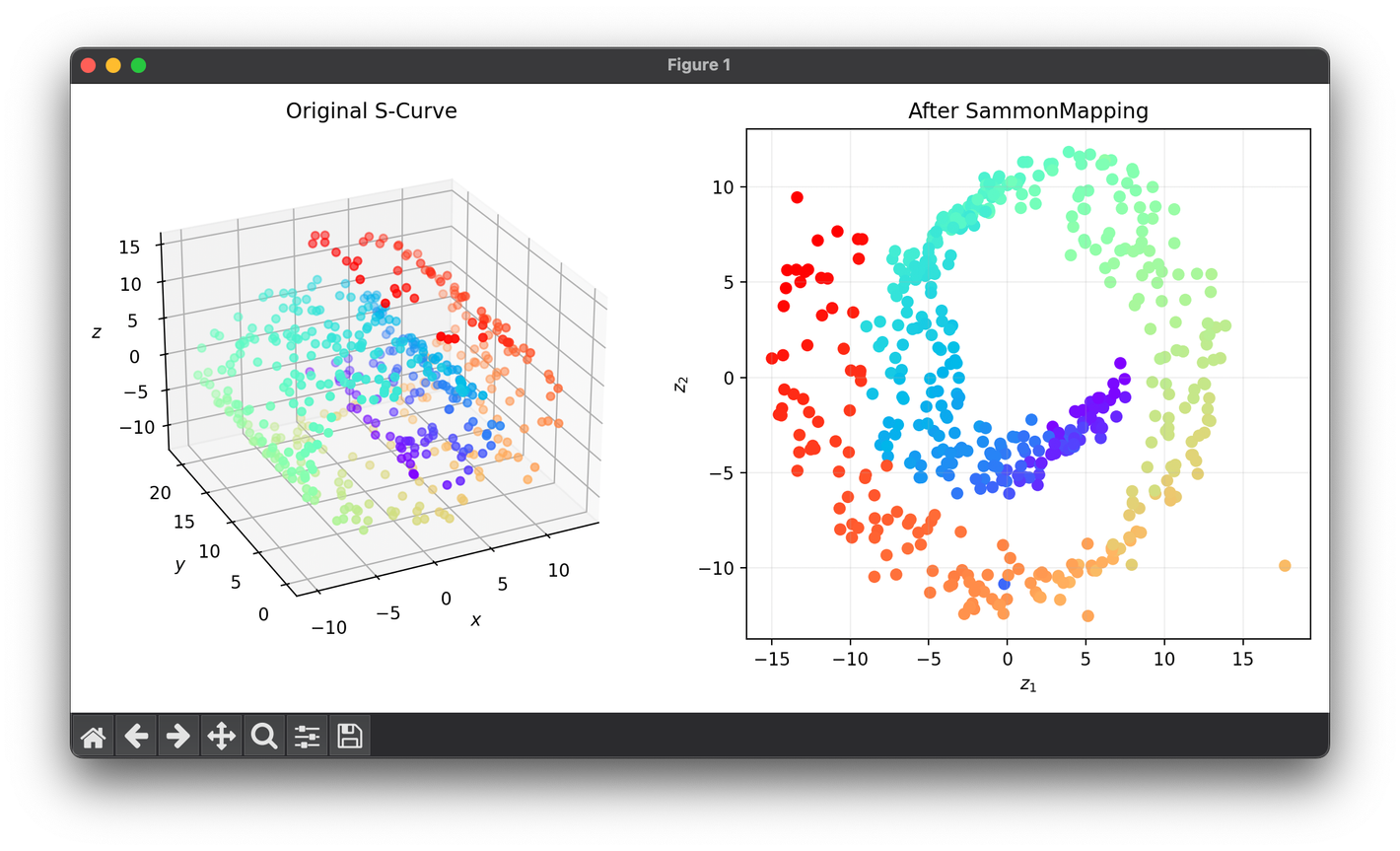

Applications

Sammon Mapping finds applications in various fields requiring visualization and analysis of high-dimensional data, such as:

• Bioinformatics: For visualizing genetic data or protein structures.
• Finance: To cluster and visualize complex financial instruments or market dynamics.
• Text Analysis: For mapping and visualizing semantic distances between documents or keywords.
• Customer Segmentation: In marketing, to identify and visualize customer groups based on purchasing behavior or preferences.

Strengths and Limitations

Strengths

• Preservation of Structure: Sammon Mapping is effective at preserving the geometry of the data, making it particularly suited for datasets where local relationships and cluster structures are more important than global distances.
• Flexibility: It can be applied to any metric space and is not limited to Euclidean distances, thus allowing for customization based on the specific characteristics of the dataset.

Limitations

• Computational Complexity: The need to compute pairwise distances between all points makes the algorithm computationally expensive, especially for large datasets.
• Local Minima: The gradient descent optimization process may converge to local minima, resulting in different outcomes depending on the initialization.
• Sensitive to Initial Mapping: The quality of the initial mapping can significantly influence the final projection, making the choice of initialization method critical.

References

1. Sammon, John W. "A nonlinear mapping for data structure analysis." IEEE Transactions on computers 100.5 (1969): 401-409.
2. Kaski, Samuel. "Dimensionality reduction by random mapping: Fast similarity computation for clustering." Proceedings of the 1998 IEEE International Joint Conference on Neural Networks Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98CH36227). Vol. 1. IEEE, 1998.
3. Borg, Ingwer, and Patrick Groenen. "Modern multidimensional scaling: Theory and applications." Journal of Educational Measurement 40.3 (2003): 277-280.