Truncated Singular Value Decomposition(SVD)

Introduction

Truncated Singular Value Decomposition (Truncated SVD) is a matrix factorization technique that reduces the dimensionality of data by truncating the Singular Value Decomposition (SVD) of a matrix. Unlike Principal Component Analysis (PCA), which requires centered data, Truncated SVD can work directly on sparse matrices without centering. This characteristic makes it particularly useful for natural language processing (NLP) tasks and other applications where data is naturally sparse and centering would lead to a loss of sparsity. Truncated SVD is also known as Latent Semantic Analysis (LSA) in the context of text processing.

Background and Theory

SVD is a fundamental matrix decomposition method in linear algebra that factorizes a matrix $A \in \mathbb{R}^{m \times n}$ into three matrices $U$, $\Sigma$, and $V^T$, where:

• $U \in \mathbb{R}^{m \times m}$ is an orthogonal matrix whose columns are the left singular vectors of $A$.
• $\Sigma \in \mathbb{R}^{m \times n}$ is a diagonal matrix with non-negative real numbers on the diagonal, known as the singular values of $A$, sorted in descending order.
• $V^T \in \mathbb{R}^{n \times n}$ is an orthogonal matrix whose rows are the right singular vectors of $A$.

The equation can be represented as:

Mathematical Foundations

Truncated SVD approximates the matrix $A$ by keeping only the first $k$ largest singular values and corresponding vectors, where $k < \min(m, n)$.

This results in the approximated matrices $\hat{U} \in \mathbb{R}^{m \times k}$, $\hat{\Sigma} \in \mathbb{R}^{k \times k}$, and $\hat{V}^T \in \mathbb{R}^{k \times n}$, and the approximation of $A$ is:

This approximation minimizes the Frobenius norm of the difference between $A$ and $A_k$ among all possible rank-$k$ approximations, making it an optimal low-rank approximation of $A$.

Procedural Steps

1. Compute SVD: Compute the full SVD of the matrix $A$.
2. Truncate: Select the first $k$ singular values and corresponding singular vectors to form $\hat{U}$, $\hat{\Sigma}$, and $\hat{V}^T$.
3. Reconstruct: Calculate $A_k = \hat{U}\hat{\Sigma}\hat{V}^T$ as the rank-$k$ approximation of $A$.

Implementation

Parameters

• n_components: int
  Dimensionality of low-space
  

Examples

Test with the iris dataset:

from luma.reduction.linear import TruncatedSVD

from sklearn.datasets import load_iris

import matplotlib.pyplot as plt
import numpy as np

iris_df = load_iris()
X = iris_df.data
y = iris_df.target

model = TruncatedSVD(n_components=2)
X_trans = model.fit_transform(X)

fig = plt.figure(figsize=(11, 5))
ax1 = fig.add_subplot(1, 2, 1, projection="3d")
ax2 = fig.add_subplot(1, 2, 2)

for cl, m in zip(np.unique(y), ["s", "o", "D"]):
    X_cl = X[y == cl]
    sc = ax1.scatter(
        X_cl[:, 0],
        X_cl[:, 1],
        X_cl[:, 2],
        c=X_cl[:, 3],
        marker=m,
        label=iris_df.target_names[cl],
    )

ax1.set_xlabel(iris_df.feature_names[0])
ax1.set_ylabel(iris_df.feature_names[1])
ax1.set_zlabel(iris_df.feature_names[2])
ax1.set_title("Original Iris Dataset")
ax1.legend()

cbar = ax1.figure.colorbar(sc, fraction=0.04)
cbar.set_label(iris_df.feature_names[3])

for cl, m in zip(np.unique(y), ["s", "o", "D"]):
    X_tr_cl = X_trans[y == cl]
    ax2.scatter(
        X_tr_cl[:, 0],
        X_tr_cl[:, 1],
        marker=m,
        edgecolors="black",
        label=iris_df.target_names[cl],
    )

ax2.set_xlabel(r"$z_1$")
ax2.set_ylabel(r"$z_2$")
ax2.set_title(
    f"Iris Dataset after {type(model).__name__} "
    + r"$(\mathcal{X}\rightarrow\mathcal{Z})$"
)
ax2.legend()
ax2.grid(alpha=0.2)

plt.tight_layout()
plt.show()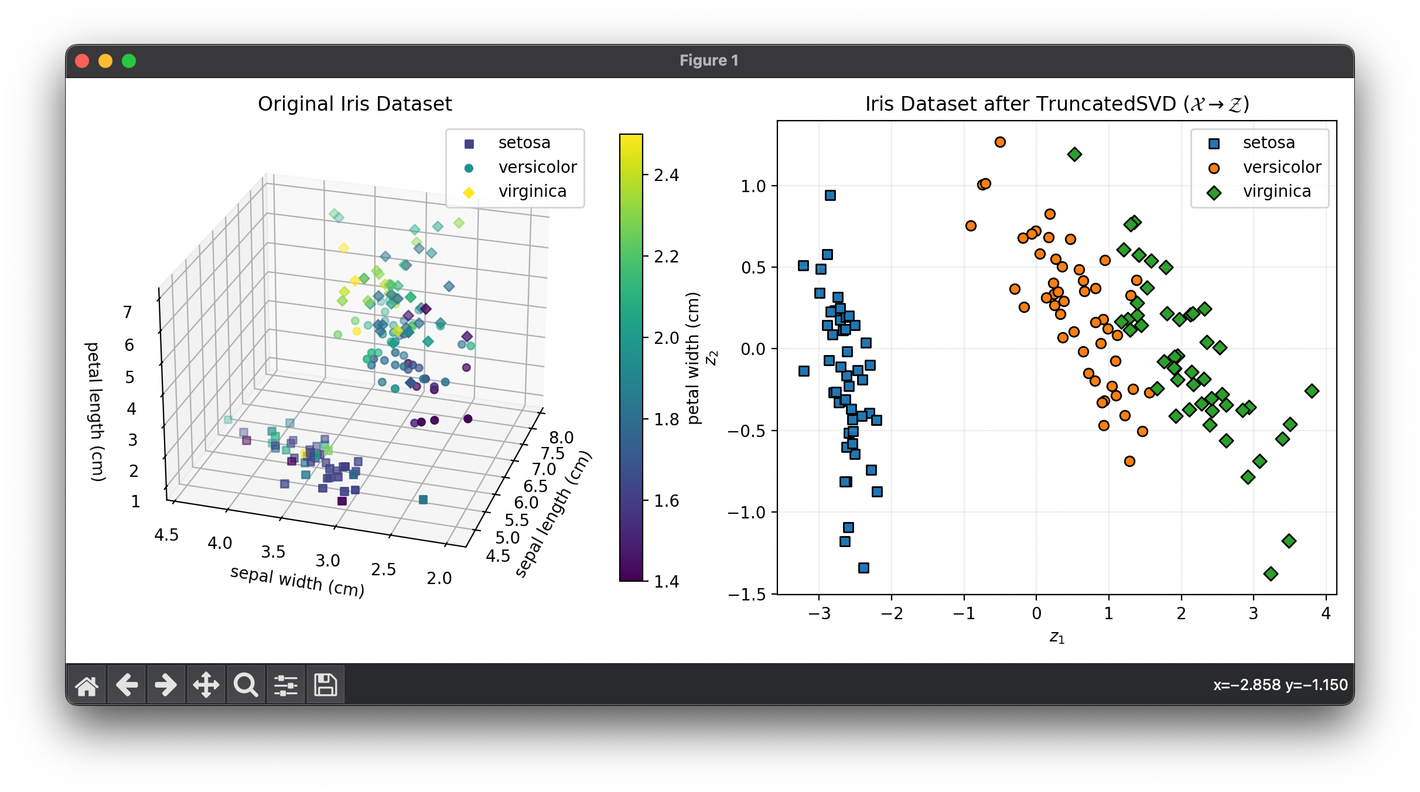

Applications

• Dimensionality Reduction: Reducing the number of features in data while preserving important information, useful in text mining, image processing, and signal processing.
• Noise Reduction: Eliminating noise by approximating the original matrix with a lower-rank matrix.
• Latent Semantic Analysis (LSA): Identifying patterns in text and relationships between terms and documents by reducing the dimensions of term-document matrices.

Strengths and Limitations

Strengths

• Efficiency with Sparse Data: Can be applied directly to sparse matrices efficiently, making it ideal for sparse datasets.
• Data Compression: Provides an efficient way to compress data by keeping only the most significant singular values and vectors.

Limitations

• Selection of $k$: The choice of $k$, the number of singular values to keep, can significantly affect the results and requires careful selection.
• Interpretability: The truncated singular vectors might be harder to interpret compared to the original features.

Advanced Topics

• Randomized Algorithms for Truncated SVD: Efficient algorithms for computing the truncated SVD of large matrices by using randomized techniques to approximate the dominant singular values and vectors.
• Incremental and Online Truncated SVD: Methods for updating the truncated SVD as new data becomes available, useful in dynamic systems where the data is continuously growing.

References

1. Halko, Nathan, Per-Gunnar Martinsson, and Joel A. Tropp. "Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions." SIAM review 53, no. 2 (2011): 217-288.
2. Deerwester, Scott, Susan T. Dumais, George W. Furnas, Thomas K. Landauer, and Richard Harshman. "Indexing by latent semantic analysis." Journal of the American society for information science 41, no. 6 (1990): 391-407.
3. Golub, Gene H., and Charles F. Van Loan. "Matrix computations." Vol. 3. Baltimore: Johns Hopkins University Press, 2012.