Random Sample Consensus (RANSAC)

Introduction

Random Sample Consensus (RANSAC) is an iterative method to estimate parameters of a mathematical model from a set of observed data that contains outliers. It is a non-deterministic algorithm in the sense that it produces a reasonable result only with a certain probability, with this probability increasing as more iterations are allowed. RANSAC is widely used in the field of computer vision, robotics, and geospatial data analysis to fit models to data with a high percentage of outliers.

Background and Theory

RANSAC was introduced by Fischler and Bolles in 1981 as a robust method to solve the problem of fitting a model to empirical data corrupted by significant levels of noise and outliers. The algorithm's fundamental assumption is that the data consists of "inliers", data points that can be explained by some set of model parameters, and "outliers" which are data points that do not fit the model.

Mathematical Foundations

The algorithm is based on randomly selecting a minimal set of points required to determine the model parameters (the minimal sample set) and then checking which of all the points in the data set are consistent with the model instantiated from this minimal set. These points are considered inliers.

Given a set of data points $\mathbf{x}_i, i = 1, 2, \ldots, N$, the goal is to find the model parameters $\mathbf{\theta}$ that best explain this data. The RANSAC algorithm proceeds as follows:

1. Random Sampling: Randomly select a minimal subset of points required to estimate the model parameters. The size of this subset depends on the problem. For example, to fit a line in 2D space, only two points are needed.
2. Model Fitting: Compute the model parameters $\mathbf{\theta}$ using the randomly selected subset.
3. Consensus Set Building: Determine the set of points from the entire dataset that fit the model instantiated with $\mathbf{\theta}$ within a predefined tolerance $\tau$. This set is called the consensus set.
4. Model Evaluation: The consensus set is used to re-estimate the model parameters, and the error of this model is calculated. If the size of the consensus set is larger than a predefined threshold or the model error is lower than a certain threshold, the current model is considered as a potential solution.
5. Iteration: Steps 1-4 are repeated for a predefined number of iterations or until a model with an acceptable error is found. The best model is the one with the largest consensus set.

Procedural Steps

The procedural implementation of RANSAC involves the following steps:

1. Initialization: Define the number of iterations $k$, the threshold $\tau$ to determine when a data point fits a model, and the number of close data points required to assert that a model fits well to data.
2. Iterate: For each iteration until $k$ is reached:
   • Randomly select a minimal subset of points and estimate the model parameters $\mathbf{\theta}$
   • Determine the consensus set of points that fit the estimated model within the threshold $\tau$
   • If the consensus set is larger than the previous largest consensus set, save the model parameters and the consensus set
3. Best Model Selection: After $k$ iterations, select the model with the largest consensus set and re-estimate the model parameters using all the points in the consensus set.
4. Final Model Evaluation: Evaluate the final model by calculating its error metric using the consensus set.

Mathematical Formulations

The success probability $P$ of the RANSAC algorithm finding a set of inliers is given by:

where:

• $P$ is the probability of success,
• $\epsilon$ is the proportion of outliers in the data,
• $s$ is the size of the minimal sample set,
• $k$ is the number of iterations.

The equation shows that as $k$ increases, the probability of success approaches 1. However, this also increases computational cost.

Implementation

Parameters

• estimator: Estimator, default = LinearRegressor()
  Regression estimator
  
• min_points: int float, default = 2
  Mininum sample size for each random sample
  
• max_iter: int, default = 1000
  Maximum iteration
  
• min_inliers: int float, default = 0.5
  Minimum number of inliers for a model to be considered valid
  
• threshold: float, default = None
  Maximum distance a point can have to be considered an inlier
  
• random_state: int, default = None
  Seed for random sampling the data
  

Examples

from luma.regressor.robust import RANSAC
from luma.visual.evaluation import ResidualPlot

import matplotlib.pyplot as plt
import numpy as np

X = np.linspace(-5, 5, 100).reshape(-1, 1)
y = (np.sin(2 * X) - X).flatten() + np.random.rand(100)

indices = np.where((-1.0 < X) & (X < 1.0))[0]
y[indices] = 3.0

model = RANSAC()
model.fit(X, y)
score = model.score(X, y)

fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)

ax1.scatter(X, y, s=10, c="black", alpha=0.4)
ax1.plot(X, model.predict(X), lw=2, c="crimson", label="Predicted Plot")
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.set_title(f"{type(model).__name__} Estimation [MSE: {score:.4f}]")
ax1.legend()
ax1.grid(alpha=0.2)

res = ResidualPlot(model, X, y)
res.plot(ax=ax2, show=True)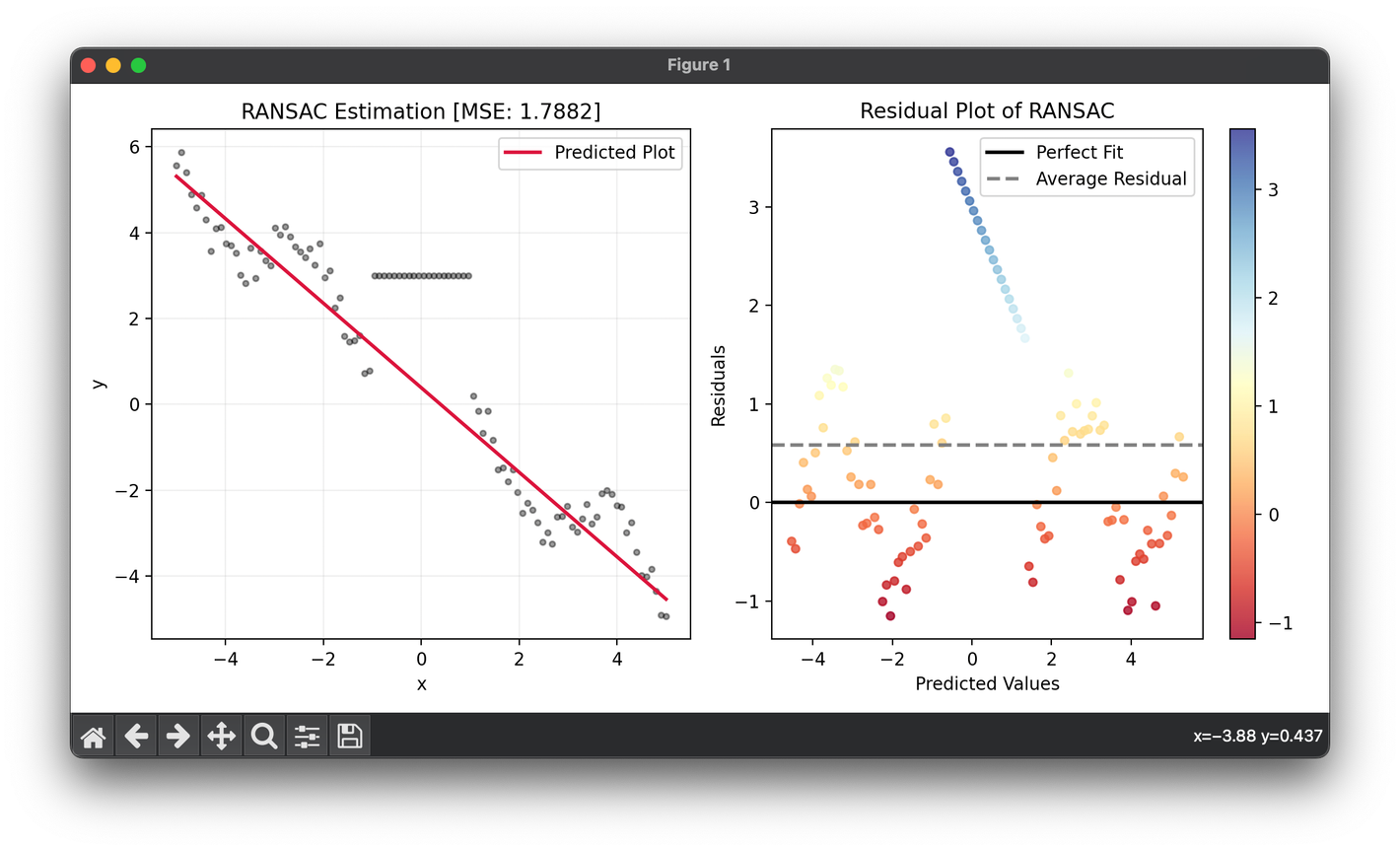

Applications

RANSAC has been successfully applied in various domains, including:

• Computer Vision: For feature matching, object detection, and 3D reconstruction.
• Robotics: For map building and localization.
• Remote Sensing: For aligning satellite imagery.

Strengths and Limitations

Strengths:

• Robustness to Outliers: RANSAC is highly effective in dealing with a large number of outliers.
• Versatility: It can be applied to a wide range of models and problems.

Limitations:

• Parameter Sensitivity: The performance of RANSAC depends heavily on the parameters (number of iterations, threshold).
• Computational Cost: The algorithm can be computationally expensive, especially for a high number of iterations.

Advanced Topics

• Adaptive RANSAC: Techniques to dynamically adjust the number of iterations based on the observed data characteristics.
• Parallel RANSAC: Implementations that leverage parallel computing to improve the computational efficiency of RANSAC.

References

1. Fischler, M. A., and Bolles, R. C. "Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography." Communications of the ACM, vol. 24, no. 6, 1981, pp. 381-395.