
01.인공 신경망(Artificial Neural Network, ANN)
인공신경망은 시냅스의 결합으로 네트워크를 형성한 인공뉴런(Node)이 학습을 통해 시냅스의 결합 세기를 변화 시켜 문제 해결 능력을 가지는 모델 전반을 의미한다. (출처: 위키백과)
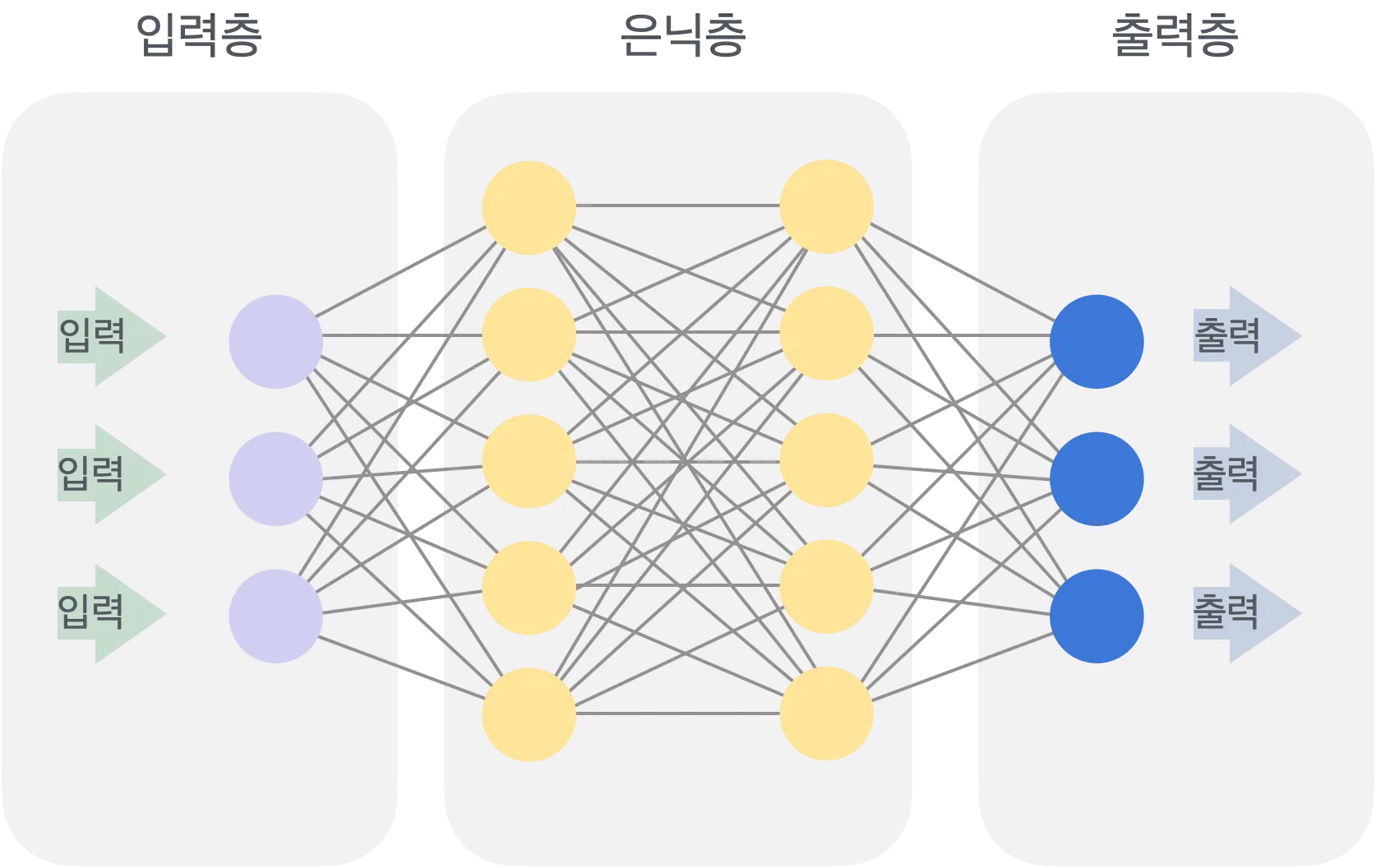
ANN (Artificial Neural Network)는 생물학적 신경망을 모방한 기계 학습 모델로, 입력층, 은닉층, 출력층으로 구성된다. 각 노드(뉴런)는 가중치를 가진 입력을 받아 활성화 함수를 통해 신호를 전달하며, 이를 통해 패턴 인식이나 데이터 예측과 같은 복잡한 문제를 해결할 수 있다. ANN은 주로 이미지 분류, 음성 인식, 자연어 처리 등의 다양한 분야에서 사용된다.
| 층 종류 | 설명 |
|---|---|
| 입력층 (Input Layer) | 데이터를 모델에 처음 전달하는 부분으로, 각 입력 데이터의 특징(feature)을 표현하는 뉴런들로 구성됨. 입력층의 뉴런 수는 입력 데이터의 특징 수와 동일함. |
| 은닉층 (Hidden Layer) | 입력층과 출력층 사이에 위치한 층으로, 데이터의 복잡한 패턴을 학습하는 역할을 함. 은닉층의 뉴런들은 비선형 변환을 통해 입력 데이터의 숨겨진 관계를 파악하며, ANN의 성능을 결정하는 중요한 요소임. |
| 출력층 (Output Layer) | 모델의 최종 예측을 제공하는 부분. 출력층의 뉴런 수는 예측하고자 하는 결과의 수와 맞추어 설정되며, 회귀, 분류 등의 문제에 따라 다른 활성화 함수를 사용함. |
1.1 ANN 간단한 실습(pytorch)
import torch # 핵심 라이브러리(pytorch)
import torch.nn as nn # 뉴런 신경망 기능 포함
import torch.optim as optim # 최적화 부분 함수가 있을 때 최소,최대를 찾을 수 있음 + @
import torchvision # 이미지 처리를 위한 라이브러리
import torchvision.transforms as transforms # 전처리를 위한 라이브러리데이터셋 로드 및 전처리
# 데이터셋 전처리
transform = transforms.Compose([
transforms.ToTensor(), # 이미지를 Tensor라고 하는 pytorch에서 사용하는 기본 자료구조로 바꿔줌
transforms.Normalize((0.5,), (0.5,)) # 이미지 정규화 -> 평균,표준편차 (0.5,0.5)
])
# MNIST 데이터셋 로드
trainset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
testset = torchvision.datasets.MNIST(root='./data', train=False, download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=False)
trainsettrainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
일반적으로 pytorch에는 데이터를 다루기 위한 여러가지 기능이 있고, 그 중 데이터를 로드하고 처리하는 부분을 DataLoader라고 하는데 일반적으로 직접 만든다. Mnist는 일반적으로 torchvision으로 제공되기 때문에 위와같은 torch.utils.data.DataLoader함수를 사용 해 주면 편하게 만들 수 있다.
-
batch_size: 배치 사이즈 만 개의 데이터가 있으면 전체학습을 하기 빡셈. 그래서 size만큼 잘게 쪼갠 단위학습을 함. 속도도 빠르고 학습시간도 빠름 -
shuffle: 데이터를 순서대로 쪼개면 순서관계 때문에 의존성이 생길 수 있다. 딥러닝에서의 기본 가정은 데이터간의 독립성을 보장하는 것인데, 이를 위해 섞어서 배치를 만들어라 하는 부분을 지정하는 것
간단한 ANN 모델 정의
class SimpleANN(nn.Module): # nn.Module 상속 받은 SimpleANN 클래스 생성
def __init__(self):
super(SimpleANN, self).__init__()
self.fc1 = nn.Linear(28 * 28, 128) # 입력층에서 은닉층으로
self.fc2 = nn.Linear(128, 64) # 은닉층에서 은닉층으로
self.fc3 = nn.Linear(64, 10) # 은닉층에서 출력층으로 최종적으로 10 개 예측
def forward(self, x):
x = x.view(-1, 28 * 28) # 입력 이미지를 1차원 벡터로 변환 (fc가 1차원 이니까)
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = self.fc3(x)
return xnn.Moulde을 상속받은 클래스를 만들어 DL을 만들기 위한 기본 기능들을 사전에 가져온다.
-
Class 내부 구조 :
부모 클래스에서 기능을 작동하는
super()함수를 불러줌. (DL의 기능을 하기 위한 기본함수 불러옴)
fc(1,2,3...): Fully Connected Layer
각 노드가 이전 레이어의 모든 노드와 연결된 신경망의 한 종류. 이를 통해 네트워크는 입력 데이터의 모든 특징(feature) 사이의 관계를 학습한다.
| 요소 | 설명 |
|---|---|
| y | 출력 벡터 (output vector) - 가중치와 입력 벡터, 편향의 연산 결과로 모델의 최종 출력값을 나타냄 |
| W | 가중치 행렬 (weight matrix) - 입력과 은닉층 또는 은닉층 간의 연결 강도를 나타내는 행렬 |
| x | 입력 벡터 (input vector) - ANN의 입력으로 사용되는 여러 개의 특징 값을 가지는 벡터 |
| b | 편향 벡터 (bias vector) - 각 뉴런의 출력에 더해지는 값으로, 출력의 유연성을 높여줌 |
가중치와 편향은 모델이 학습하는 과정에서 조정한다.
-
nn.Linear: ANN을 만드는 함수. layer에서 입력과 출력을 지정해 줘야 한다. 입력 몇개 출력 몇개 << 이런 식으로 why? 이전 layer에서 어떤 것과 연결될 지 모르고 앞으로 어떤 layer와 연결될 지 모르기 때문에 그 정보를 제공해 준다. -
nn.Linear(28\*28, 128)에서 "28*28"은 사용할 Mnist의Data크기라고 생각하면 된다.
- forward : layer들의 연결관계를 나타내는 함수
view 살펴보기
x.view(-1,28*28)에서
view()는 PyTorch에서 텐서의 크기(모양)을 변경하는 함수
-1은 "나는 배치 크기를 모른다, 알아서 계산해 줘!" 라고 PyTorch에게 말하는 것이다.
딥러닝 모델은 보통 여러 개의 데이터를 한 번에 처리합니다. 이 여러 개의 데이터를 묶은 것을 배치(batch)라고 부릅니다.
예를 들어, 한 번에 64개의 이미지를 모델에 입력한다고 할 때, 이 배치를 표현하면 (64, 28, 28)의 형태를 가집니다. 여기서 64는 배치 크기, 그리고 28, 28은 각각의 이미지의 가로, 세로 크기입니다.
view() 함수에서 -1의 의미:
이 배치 데이터를 Fully Connected Layer에 전달하기 위해 1차원 벡터 형태로 변환하려고 합니다.
(64, 28, 28) 크기의 텐서를 1차원 벡터로 펼치는 것이 필요합니다. 각 이미지가 28 x 28 = 784이므로, 하나의 이미지당 784개의 값을 가진 벡터로 변환됩니다.
이때, view(-1, 28 28)에서 -1의 의미는, 배치 크기를 그대로 유지하라는 뜻입니다. 배치 크기가 몇이든 관계없이, PyTorch가 자동으로 그 값을 계산하도록 지시하는 것입니다.
즉, (64, 28, 28) 크기의 텐서를 view(-1, 28 28)로 변환하면, 결과는 (64, 784)가 됩니다.
결과적으로:
-1을 사용하면 PyTorch가 현재 배치 크기를 자동으로 계산해줍니다. 따라서, 우리가 몇 개의 이미지를 가지고 있는지(배치 크기)가 달라지더라도 view(-1, 28 28)은 그 크기를 자동으로 맞춰 줍니다.
예를 들어, 배치 크기가 128이라면 (128, 28, 28) 크기의 텐서를 view(-1, 28 28)로 변환하면 결과는 (128, 784)가 됩니다.
-
torch.relu(self.fc1(x)): 활성화 함수 -->fc1레이어인 입력 레이어에 x를 전달한 다음 이 출력을 다시relu를 적용한 값으로 바꾸고 다시 x에 저장함. -
최종적으로
x= self.fc3(x)에서x = (64,10)이 나올 것이다.
데이터는 64개고 최종 출력 레이어는 10차원에 있기 때문이다.
학습 전 모델 예측하기
# 학습 전 모델 예측
model = SimpleANN()
correct = 0
total = 0
with torch.no_grad(): # 평가단계에서 기울기를 계산하지 않는다.
for data in testloader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print(f'Accuracy of the network on the 10000 test images: {100 * correct / total:.2f}%')torch.no_grad() : 학습을 진행하지 않는다.
왜 torch.max()를 사용할까?
- 출력 단계에서 10개를 모두 출력했고, 10개의 퍼셉트론에 각 확률이 적혀있다고 생각하면, 그 확률이 가장 큰 값을 찾아줘야 하기 때문에 max함수를 사용
모델의 예측 정확도를 계산
total += labels.size(0)
correct += (predicted == labels).sum().item()labels.size(0):
labels는 배치 내의 정답 레이블들을 가지고 있는 텐서다.
size(0)은 텐서의 첫 번째 차원의 크기. 이 첫 번째 차원은 배치 크기를 나타내므로, labels.size(0)은 현재 배치에 포함된 샘플의 수다.
예를 들어, labels가 (64,) 크기를 가진다면 이는 64개의 레이블이 있음을 의미하므로, labels.size(0)은 64다.
total += labels.size(0):
이 코드는 지금까지 처리한 총 샘플 수를 누적해서 더해가는 역할.
각 배치마다 해당 배치에 포함된 샘플 수를 total에 더함으로써, 전체 데이터셋에서 처리한 총 샘플의 수를 추적하는 것.
이를 통해 전체 데이터셋의 총 레이블 수를 total 변수에 저장.
correct += (predicted == labels).sum().item()
predicted == labels:
predicted는 모델이 현재 배치에 대해 예측한 클래스 레이블을 나타내고, labels는 해당 배치에 대한 실제 정답 레이블.
(predicted == labels)는 각 샘플의 예측이 정답과 일치하는지를 비교.
결과는 같은 크기를 가진 불리언 텐서(Boolean tensor)로, 맞는 경우 True, 틀린 경우 False 값을 가진다.
예를 들어, predicted = [1, 0, 1]이고 labels = [1, 0, 0]이라면 (predicted == labels)은 [True, True, False]가 된다.
(predicted == labels).sum():
(predicted == labels)의 결과는 불리언 텐서이지만, sum() 함수를 사용하면 True는 1로, False는 0으로 계산.
이 부분은 올바르게 예측된 샘플의 수를 계산하는 것.
예를 들어, (predicted == labels)의 결과가 [True, True, False]라면, .sum()은 2다. 즉, 두 개의 샘플이 올바르게 예측된 것.
.item():
.item()은 파이토치 텐서에서 값을 Python의 기본 데이터 타입 (예: int, float)으로 변환해주는 역할.
여기서는 sum()의 결과를 텐서가 아닌 정수 값으로 변환하여 correct에 더한다.
correct += (predicted == labels).sum().item():
이 코드는 지금까지 맞춘 정확한 예측의 개수를 correct 변수에 누적해서 더해가는 역할.
각 배치마다 올바르게 예측된 샘플의 수를 누적하여, 전체 데이터셋에서 정확히 예측된 샘플의 총 개수를 추적.
모델 학습
# 모델 초기화
model = SimpleANN() # SimpleANN 클래스의 인스턴스 생성
# 손실 함수와 최적화 알고리즘 정의
criterion = nn.CrossEntropyLoss() # 분류 문제에 사용되는 손실 함수로, 모델의 예측 값과 실제 레이블 값 사이의 차이를 계산
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9) # 경사 하강법(SGD)을 통해 모델의 파라미터를 최적화 (lr: 학습률, momentum: 학습 가속도)
# 모델 학습
epochs = 10 # 전체 데이터셋을 10번 반복 학습 (에포크 수)
for epoch in range(epochs):
running_loss = 0.0 # 에포크 동안 손실값을 누적하여 로그를 남기기 위함
# 데이터 로더를 통해 배치 단위로 데이터 불러오기
for i, data in enumerate(trainloader, 0): # trainloader에서 데이터를 배치 단위로 불러오며 인덱스도 함께 가져옴 (i는 인덱스)
inputs, labels = data # 입력 데이터와 실제 레이블을 data에서 분리
# 기울기 초기화 (이전 배치의 기울기를 제거)
optimizer.zero_grad()
# 순전파 + 손실 계산 + 역전파 + 최적화
outputs = model(inputs) # 입력 데이터를 모델에 통과시켜 예측 값(outputs) 생성
loss = criterion(outputs, labels) # 예측 값과 실제 레이블 간 손실 계산
loss.backward() # 역전파를 통해 각 파라미터에 대한 기울기 계산 (손실 값을 기준으로 파라미터 업데이트 방향을 계산)
optimizer.step() # 기울기를 바탕으로 가중치 업데이트 (파라미터 최적화)
# 손실 출력 (중간중간 손실 로그를 남겨 학습 상황을 모니터링)
running_loss += loss.item() # 현재 배치의 손실 값을 running_loss에 누적
if i % 100 == 99: # 매 100 미니배치마다 손실 값을 출력
print(f'[Epoch {epoch + 1}, Batch {i + 1}] loss: {running_loss / 100:.3f}')
running_loss = 0.0 # 로그 출력 후 손실 값 초기화
print('Finished Training')결과값
[Epoch 1, Batch 100] loss: 1.344
[Epoch 1, Batch 200] loss: 0.490
[Epoch 1, Batch 300] loss: 0.352
[Epoch 1, Batch 400] loss: 0.342
[Epoch 1, Batch 500] loss: 0.302
[Epoch 1, Batch 600] loss: 0.290
[Epoch 1, Batch 700] loss: 0.268
[Epoch 1, Batch 800] loss: 0.234
[Epoch 1, Batch 900] loss: 0.237
[Epoch 2, Batch 100] loss: 0.198
[Epoch 2, Batch 200] loss: 0.185
[Epoch 2, Batch 300] loss: 0.186
[Epoch 2, Batch 400] loss: 0.183
[Epoch 2, Batch 500] loss: 0.190
[Epoch 2, Batch 600] loss: 0.181
[Epoch 2, Batch 700] loss: 0.155
[Epoch 2, Batch 800] loss: 0.158
[Epoch 2, Batch 900] loss: 0.160
.
.
.
[Epoch 9, Batch 900] loss: 0.060
[Epoch 10, Batch 100] loss: 0.033
[Epoch 10, Batch 200] loss: 0.043
[Epoch 10, Batch 300] loss: 0.041
[Epoch 10, Batch 400] loss: 0.047
[Epoch 10, Batch 500] loss: 0.054
[Epoch 10, Batch 600] loss: 0.059
[Epoch 10, Batch 700] loss: 0.048
[Epoch 10, Batch 800] loss: 0.048
[Epoch 10, Batch 900] loss: 0.052
Finished Training모델 평가
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print(f'Accuracy of the network on the 10000 test images: {100 * correct / total:.2f}%')결과값
Accuracy of the network on the 10000 test images: 96.83%
02. 합성곱신경망(Convolutional Neural Network,CNN)
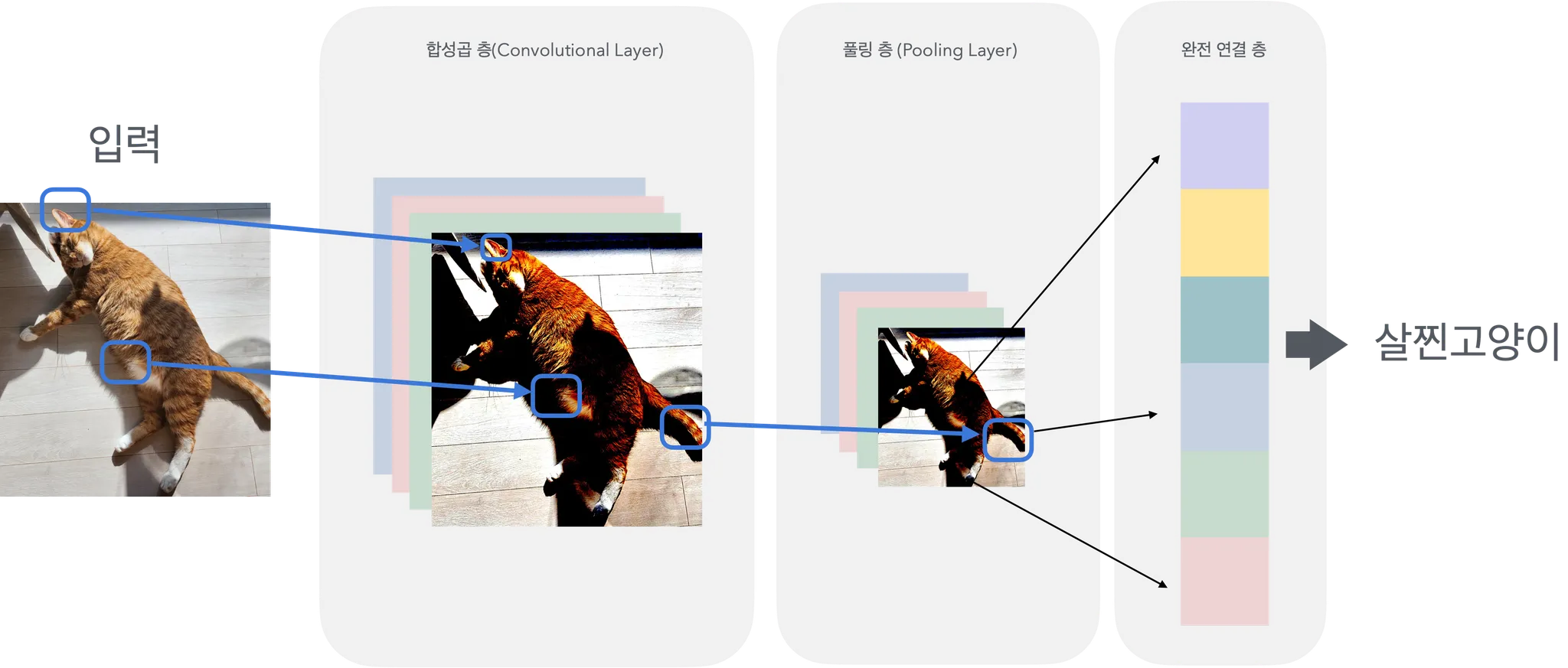
출처 : 스파르타코딩클럽
2-1. CNN의 주요 개념과 구조
이미지 특화된 CNN
CNN은 이미지나 영상 데이터 같은 다차원 데이터를 효과적으로 처리하기 위해 설계된 인공 신경망의 일종이다. 합성곱 연산을 통해 입력 데이터에서 패턴을 추출하고, 이를 기반으로 분류나 예측을 수행한다.(CNN은 출력 layer에는 적합하지 않기 때문에, 마지막에 완전 연결층을 출력 layer로 두며 ANN을 활용한다)
- Layer
-
합성곱 층 (Convolutional Layer):
-
입력 데이터에 필터(또는 커널)를 적용하여 특징 맵(feature map)을 생성한다.
-
합성곱 층은 데이터에서 지역적인 패턴을 학습하며, 필터의 크기와 개수를 통해 다양한 특징을 추출한다.
-
nn.Conv2d함수를 사용하여 합성곱 층을 정의한다.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0)in_channels: 입력 이미지의 채널 수. 예를 들어, 흑백 이미지의 경우 1, 컬러 이미지의 경우 3이다.out_channels: 필터의 개수, 즉 출력 특징 맵의 채널 수이다.kernel_size: 필터의 크기. 예를 들어 (3, 3) 또는 3으로 정의할 수 있다.stride: 필터가 이동하는 간격을 의미한다.padding: 입력 이미지의 가장자리를 감싸는 패딩의 크기이다. 패딩을 통해 출력 크기를 조정할 수 있다.
-
-
풀링 층 (Pooling Layer):
- 특징 맵의 크기를 줄여 계산량을 줄이고, 오버피팅을 방지한다. 주로 Max Pooling(최대값)과 Average Pooling(평균값)이 사용된다.
- 풀링 층은 Local 특징 중에서 중요한 값만 유지한다.
- nn.MaxPool2d를 사용해 풀링을 정의할 수 있다.
nn.MaxPool2d(kernel_size, stride=None, padding=0)kernel_size: 풀링 필터의 크기이다.stride: 풀링 필터의 이동 간격이다. 기본적으로는 kernel_size와 동일하다.padding: 풀링 전에 입력 데이터에 패딩을 추가할 수 있다.
-
완전 연결 층 (Fully Connected Layer):
- 합성곱과 풀링 과정을 통해 추출된 특징을 바탕으로 최종적으로 분류 작업을 수행한다.
- nn.Linear를 사용해 층을 정의한다.
-
활성화 함수 (Activation Function)
활성화 함수는 각 층에서 비선형성을 추가하기 위해 사용된다. CNN에서는 주로
ReLU (Rectified Linear Unit)가 사용된다. 이는 음수 값을 0으로 변환하여 네트워크에 비선형 특성을 부여한다.
F.relu()는 입력 값 x의 음수를 모두 0으로 변환한다.- ReLU 함수 적용 방법:
import torch.nn.functional as F
x = F.relu(x)- CNN의 전체 구성 및 흐름
예시:
import torch
import torch.nn as nn
import torch.nn.functional as F
class SimpleCNN(nn.Module):
def __init__(self):
super(SimpleCNN, self).__init__()
# 첫 번째 합성곱 층 정의: 입력 채널 1, 출력 채널 6, 커널 크기 3x3
self.conv1 = nn.Conv2d(1, 6, 3)
# 두 번째 합성곱 층 정의: 입력 채널 6, 출력 채널 16, 커널 크기 3x3
self.conv2 = nn.Conv2d(6, 16, 3)
# 완전 연결 층 정의
self.fc1 = nn.Linear(16 * 6 * 6, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# 첫 번째 합성곱 층과 ReLU, 그리고 Max Pooling 적용
x = F.relu(self.conv1(x))
x = F.max_pool2d(x, 2)
# 두 번째 합성곱 층과 ReLU, 그리고 Max Pooling 적용
x = F.relu(self.conv2(x))
x = F.max_pool2d(x, 2)
# 데이터의 차원 변환 (Flatten): (배치 크기, -1)
x = x.view(-1, 16 * 6 * 6)
# 완전 연결 층을 통과시키며 ReLU 적용
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
# 최종 출력 층
x = self.fc3(x)
return x
# 모델 인스턴스 생성
model = SimpleCNN()- 합성곱과 활성화: 입력 데이터를 필터로 감지하며 각 필터는 특정 특징을 추출한다. conv1, conv2와 같은 합성곱 층을 통과하면서 점점 더 복잡한 특징이 추출된다.
- 풀링: Max Pooling을 사용하여 데이터 크기를 줄여 중요한 정보만 남긴다.
- Flatten: 마지막 합성곱 층에서 나온 결과를 완전 연결 층에 넣기 위해 1차원 벡터 형태로 변환한다.
- x.view(-1, 16 6 6)에서 -1은 배치 크기를 자동으로 계산하는 역할을 한다.
- 완전 연결 층과 분류: 마지막 단계에서 추출된 특징 벡터를 이용해 최종적으로 각 클래스에 대한 확률 값을 예측한다.
CNN은 이미지 데이터에서 특징을 자동으로 추출하여 이를 바탕으로 예측을 수행하는 딥러닝 모델이다. 합성곱 층에서 특징을 추출하고, 풀링 층에서 크기를 줄이며, 마지막으로 완전 연결 층을 통해 예측을 수행하는 것이 CNN의 주요 학습 흐름이다. 이러한 구조 덕분에 CNN은 이미지 분류, 객체 탐지 등 컴퓨터 비전 문제에서 큰 성과를 내고 있다.
2-2 CNN 간단한 실습
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
# 데이터셋 전처리
transform = transforms.Compose([
transforms.ToTensor(), # 이미지를 PyTorch 텐서로 변환 (픽셀 값의 범위가 [0, 1]로 스케일링됨). 이 작업은 이미지 데이터를 파이토치 모델이 처리할 수 있는 형태로 변환함
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)) # 각 채널(R, G, B)에 대해 평균 0.5, 표준편차 0.5로 정규화. 이는 데이터의 범위를 [-1, 1]로 변환하여 학습을 안정화하고, 신경망이 더 빠르게 수렴하도록 돕는 역할을 함
])
# CIFAR-10 데이터셋 로드
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform) # CIFAR-10 학습 데이터셋 로드, 필요 시 다운로드, 전처리 적용
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True) # 학습 데이터셋을 배치 크기 64로 나누고, 랜덤하게 섞어서 불러옴
testset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform) # CIFAR-10 테스트 데이터셋 로드, 필요 시 다운로드, 전처리 적용
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=False) # 테스트 데이터셋을 배치 크기 64로 나누고, 순차적으로 불러옴
# SimpleCNN 클래스 정의
class SimpleCNN(nn.Module):
def __init__(self):
super(SimpleCNN, self).__init__()
self.conv1 = nn.Conv2d(3, 32, 3, padding=1) # 첫 번째 합성곱 층: 입력 채널 3 (RGB 이미지), 출력 채널 32, 커널 크기 3x3, 패딩 1 (출력 크기를 입력과 동일하게 유지)
self.pool = nn.MaxPool2d(2, 2) # 최대 풀링 층: 풀링 크기 2x2, 스트라이드 2 (입력의 크기를 절반으로 줄임)
self.conv2 = nn.Conv2d(32, 64, 3, padding=1) # 두 번째 합성곱 층: 입력 채널 32, 출력 채널 64, 커널 크기 3x3, 패딩 1 (출력 크기를 입력과 동일하게 유지)
self.fc1 = nn.Linear(64 * 8 * 8, 512) # 완전 연결 층: 입력 차원 64*8*8 (Conv2 이후의 출력 크기 플래튼), 출력 차원 512
self.fc2 = nn.Linear(512, 10) # 출력 층: 10개의 클래스 (CIFAR-10의 클래스 수)
def forward(self, x):
x = self.pool(torch.relu(self.conv1(x))) # 첫 번째 합성곱 층 -> ReLU 활성화 함수 -> 최대 풀링 적용
x = self.pool(torch.relu(self.conv2(x))) # 두 번째 합성곱 층 -> ReLU 활성화 함수 -> 최대 풀링 적용
x = x.view(-1, 64 * 8 * 8) # 텐서를 플래튼(flatten)하여 완전 연결 층에 전달 (배치 크기는 유지하며 나머지 차원을 일렬로 펼침)
x = torch.relu(self.fc1(x)) # 첫 번째 완전 연결 층 -> ReLU 활성화 함수 적용
x = self.fc2(x) # 두 번째 완전 연결 층 (출력 층)
return x
# 모델 초기화
model = SimpleCNN() # SimpleCNN 클래스의 인스턴스 생성 (합성곱 신경망 모델)
# 손실 함수와 최적화 알고리즘 정의
criterion = nn.CrossEntropyLoss() # 분류 문제에 사용되는 손실 함수로, 모델의 예측 값과 실제 레이블 값 사이의 차이를 계산
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9) # 경사 하강법(SGD)을 통해 모델의 파라미터를 최적화 (lr: 학습률, momentum: 학습 가속도)
# 모델 학습
epochs = 10 # 전체 데이터셋을 10번 반복 학습 (에포크 수)
for epoch in range(epochs):
running_loss = 0.0 # 에포크 동안 손실값을 누적하여 로그를 남기기 위함
# 데이터 로더를 통해 배치 단위로 데이터 불러오기
for i, data in enumerate(trainloader, 0): # trainloader에서 데이터를 배치 단위로 불러오며 인덱스도 함께 가져옴 (i는 인덱스)
inputs, labels = data # 입력 데이터와 실제 레이블을 data에서 분리
# 기울기 초기화 (이전 배치의 기울기를 제거)
optimizer.zero_grad()
# 순전파 + 손실 계산 + 역전파 + 최적화
outputs = model(inputs) # 입력 데이터를 모델에 통과시켜 예측 값(outputs) 생성
loss = criterion(outputs, labels) # 예측 값과 실제 레이블 간 손실 계산
loss.backward() # 역전파를 통해 각 파라미터에 대한 기울기 계산 (손실 값을 기준으로 파라미터 업데이트 방향을 계산)
optimizer.step() # 기울기를 바탕으로 가중치 업데이트 (파라미터 최적화)
# 손실 출력 (중간중간 손실 로그를 남겨 학습 상황을 모니터링)
running_loss += loss.item() # 현재 배치의 손실 값을 running_loss에 누적
if i % 100 == 99: # 매 100 미니배치마다 손실 값을 출력
print(f'[Epoch {epoch + 1}, Batch {i + 1}] loss: {running_loss / 100:.3f}') # 에포크와 배치 번호를 포함해 평균 손실 값 출력
running_loss = 0.0 # 로그 출력 후 손실 값 초기화
print('Finished Training') 결과값
[Epoch 1, Batch 100] loss: 2.127
[Epoch 1, Batch 200] loss: 1.786
[Epoch 1, Batch 300] loss: 1.603
[Epoch 1, Batch 400] loss: 1.484
[Epoch 1, Batch 500] loss: 1.426
[Epoch 1, Batch 600] loss: 1.367
[Epoch 1, Batch 700] loss: 1.330
.
.
.
[Epoch 10, Batch 100] loss: 0.058
[Epoch 10, Batch 200] loss: 0.044
[Epoch 10, Batch 300] loss: 0.047
[Epoch 10, Batch 400] loss: 0.059
[Epoch 10, Batch 500] loss: 0.062
[Epoch 10, Batch 600] loss: 0.071
[Epoch 10, Batch 700] loss: 0.072
Finished Training# 모델 평가
correct = 0 # 올바르게 예측한 샘플 수
total = 0 # 전체 샘플 수
with torch.no_grad(): # 평가 단계에서는 기울기를 계산하지 않음 (메모리 절약 및 속도 향상)
for data in testloader: # 테스트 데이터 로더를 통해 데이터 반복
images, labels = data # 입력 이미지와 실제 레이블을 분리
outputs = model(images) # 모델을 통해 예측 값(outputs) 생성
_, predicted = torch.max(outputs.data, 1) # 각 샘플에 대해 가장 높은 값(확률)을 가지는 클래스 예측
total += labels.size(0) # 전체 샘플 수 누적
correct += (predicted == labels).sum().item() # 올바르게 예측한 샘플 수 누적
print(f'Accuracy of the network on the 10000 test images: {100 * correct / total:.2f}%') # 전체 테스트 데이터에 대한 모델의 정확도 출력결과값
Accuracy of the network on the 10000 test images: 72.47%
03. 순환신경망(Recurrent Neural Network, RNN)
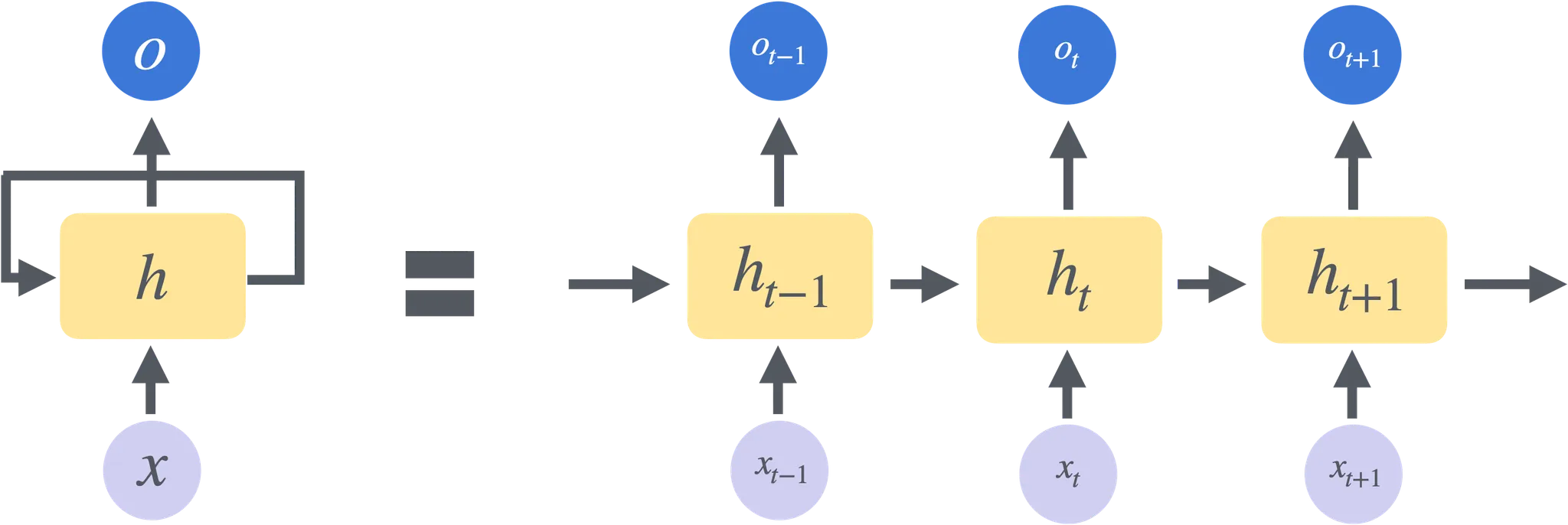
출처 : 스파르타코딩클럽
기본 개념
RNN (Recurrent Neural Network)
순차적인 데이터를 처리하고 순서에 따른 의존성을 학습하는 데 사용되는 인공 신경망의 일종이다. RNN은 시간에 따라 변화하는 데이터, 즉 시계열 데이터를 잘 처리할 수 있는 구조를 가지고 있으며, 특히 텍스트, 음성, 비디오 프레임 같은 연속적인 데이터에 적합하다.
-
순환 구조
- RNN의 핵심은 순환(recurrence) 구조에 있다. 일반적인 신경망은 입력과 출력 사이에 단방향으로 연결되지만, RNN은 이전 단계의 출력을 현재 단계의 입력으로 다시 사용한다.
- 이를 통해 RNN은 이전 정보를 기억하고 현재의 예측에 반영할 수 있어, 문맥(context)이나 시간 의존성을 다룰 수 있다.
-
기억과 시간 의존성
- RNN은 시간에 따른 상태(state)를 가지며, 이는 마치 인간의 단기 기억처럼 이전 정보를 저장하고 이를 바탕으로 현재 단계의 예측에 영향을 준다.
- 예를 들어, 문장 내에서 단어를 예측할 때, RNN은 앞서 나온 단어들의 정보를 기억하고 이를 이용해 다음 단어를 예측할 수 있다.
-
셀(state) 업데이트
- RNN은 매 시점마다 셀 상태(hidden state)를 업데이트하여 이전의 정보와 새로운 입력 정보를 결합한다.
- 이 업데이트는 반복(recurrent) 계산을 통해 이루어지며, 현재 단계의 출력과 다음 단계의 입력을 함께 고려해 계산된다.
RNN의 한계와 개선
- 장기 의존성 문제: 기본 RNN은 오래된 정보를 기억하는 데 어려움이 있다. 이는 학습 중에 기울기 소실(vanishing gradient) 문제 때문인데, 이로 인해 과거의 정보를 학습하기 어려워진다.
- 이러한 문제를 해결하기 위해 LSTM(Long Short-Term Memory)과 GRU(Gated Recurrent Unit) 같은 구조가 도입되었다. 이들은 게이트(gate)를 사용해 중요한 정보는 잘 기억하고, 불필요한 정보는 잊도록 설계되어 장기 의존성 문제를 해결한다.
RUN의 주요 사용 사례
- 자연어 처리(NLP): 텍스트 생성, 번역, 감정 분석, 문장 완성 등에서 RNN은 매우 효과적이다.
- 시계열 데이터 분석: 주가 예측, 날씨 예측과 같이 시간에 따른 변화를 예측하는 데 사용된다.
- 음성 인식: 음성 데이터를 시간 흐름에 따라 처리해, 사람의 말을 텍스트로 변환하는 데 사용된다.
04. LSTM(Long Short-Term Memory)와 GRU(Gated Recurrent Unit)
1. LSTM (Long Short-Term Memory)
LSTM은 기본 RNN의 한계인 기울기 소실 문제(vanishing gradient problem)를 해결하기 위해 기억 셀(cell state)과 게이트(gate) 구조를 도입한 신경망이다. LSTM은 중요한 정보는 기억하고, 필요 없는 정보는 버리는 과정을 통해 학습한다.
LSTM의 주요 구성 요소
- 셀 상태 (Cell State): LSTM은 데이터를 저장할 수 있는 긴 시퀀스를 기억하는 경로를 제공하는 셀 상태를 가지고 있다. 이 셀 상태는 정보를 유지하거나 제거하는 경로로, 정보가 흐르면서 중요한 부분만 유지한다.
- 게이트 (Gates): LSTM은 데이터를 관리하는 세 가지 게이트를 사용한다.
- 입력 게이트 (Input Gate): 새로운 정보를 셀 상태에 얼마나 반영할지 결정한다.
- 망각 게이트 (Forget Gate): 현재 셀 상태에서 어떤 정보를 버릴지 결정한다. 이게 LSTM이 장기 의존성 문제를 해결하는 데 중요한 역할을 한다.
- 출력 게이트 (Output Gate): 현재 셀 상태로부터 최종 출력 값을 결정한다.
LSTM의 동작 원리
- Forget Gate를 통해 이전 셀 상태에서 불필요한 정보를 제거한다.
- Input Gate를 통해 새로운 입력 정보를 셀 상태에 반영한다.
- Output Gate를 통해 셀 상태와 현재 상태를 조합해 최종 출력을 생성한다.
이렇게 세 개의 게이트를 통해 LSTM은 과거 정보를 효율적으로 관리하고, 필요 없는 정보를 버리며 중요한 정보는 계속 기억하게 된다.
2. GRU (Gated Recurrent Unit)
GRU는 LSTM의 간소화된 버전으로, 비슷한 역할을 하지만 구조가 더 단순하다. LSTM은 여러 게이트가 존재해 구조가 복잡하고 학습 속도가 느릴 수 있는 반면, GRU는 더 적은 수의 게이트로 비슷한 성능을 낸다.
GRU의 주요 구성 요소
- 업데이트 게이트 (Update Gate): GRU에서는 입력 게이트와 망각 게이트를 하나로 합친 업데이트 게이트가 존재한다. 이 게이트는 과거의 정보를 얼마나 유지할지를 결정하며, 학습 중에 기억해야 할 정보와 잊어야 할 정보를 제어한다.
- 리셋 게이트 (Reset Gate): 리셋 게이트는 이전 상태를 얼마나 무시할지를 결정하여 새로운 입력을 더 강하게 반영할지 조정한다.
GRU의 동작 원리
- Reset Gate를 통해 이전 상태를 얼마나 반영할지 결정하고, 새로운 입력과 결합한다.
- Update Gate를 통해 과거 정보를 유지하거나 업데이트할지 결정하여 최종 출력을 생성한다.
LSTM과 GRU의 차이점
구조:
- LSTM은 세 개의 게이트(입력, 망각, 출력 게이트)와 셀 상태를 가지며, 구조가 복잡하지만 더 강력한 기억 능력을 가지고 있다.
- GRU는 두 개의 게이트(업데이트, 리셋 게이트)만을 사용하고 셀 상태가 따로 없으며, 구조가 단순하다.
연산 비용:
- LSTM은 더 복잡한 구조를 가지고 있어 계산 비용이 더 크지만, 더 강력한 표현 능력을 가진다.
- GRU는 계산 비용이 LSTM보다 적고 학습 속도가 더 빠르다. 따라서 연산 자원이 제한된 경우나 더 빠른 학습이 필요한 경우에 유리하다.
성능:
- 특정 작업에서는 LSTM과 GRU가 비슷한 성능을 보이나, 데이터의 의존성이 긴 경우(예: 장기적인 문맥을 이해해야 하는 경우)에는 LSTM이 더 좋은 성능을 낼 수 있다.
- GRU는 LSTM보다 적은 파라미터 수를 가지고 있어, 데이터가 충분하지 않은 경우나 학습 속도가 중요한 상황에서 더 유리하다.
간단한 RNN , LSTM 실습하기
RNN
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# 데이터 생성 및 전처리
# Sine 파형 데이터 생성
def create_sine_wave_data(seq_length, num_samples):
X = [] # 입력 시퀀스를 저장할 리스트
y = [] # 출력 시퀀스를 저장할 리스트
for _ in range(num_samples):
start = np.random.rand() # 0과 1 사이의 임의의 시작점을 생성
x = np.linspace(start, start + 2 * np.pi, seq_length) # 시작점부터 2파이 만큼의 범위를 seq_length 개수만큼 균등하게 나눔
X.append(np.sin(x)) # 입력 시퀀스로 사인 값을 추가
y.append(np.sin(x + 0.1)) # 출력 시퀀스로 입력 시퀀스를 약간 이동시킨 사인 값을 추가 (예측할 목표값)
return np.array(X), np.array(y) # 입력과 출력 시퀀스를 NumPy 배열로 반환
seq_length = 50 # 각 시퀀스의 길이 (50개의 시점 데이터)
num_samples = 1000 # 생성할 샘플의 총 개수
X, y = create_sine_wave_data(seq_length, num_samples) # Sine 파형 데이터 생성
# 데이터셋을 PyTorch 텐서로 변환
X = torch.tensor(X, dtype=torch.float32).unsqueeze(-1) # NumPy 배열을 PyTorch 텐서로 변환하고, 마지막 차원에 추가하여 (batch_size, seq_length, 1) 형태로 만듦
y = torch.tensor(y, dtype=torch.float32).unsqueeze(-1) # 위와 같당
# 간단한 RNN 모델 정의
# SimpleRNN 클래스 정의
class SimpleRNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleRNN, self).__init__()
self.rnn = nn.RNN(input_size, hidden_size, batch_first=True) # RNN 레이어 정의: 입력 크기, 은닉 상태 크기, batch_first=True는 입력 텐서의 배치 크기가 첫 번째 차원임을 의미함
self.fc = nn.Linear(hidden_size, output_size) # 완전 연결 층 정의: 은닉 상태 크기에서 출력 크기로 변환
def forward(self, x):
# RNN의 초기 은닉 상태를 정의. 모든 값이 0인 텐서로 초기화 (크기는 (num_layers, batch_size, hidden_size))
h0 = torch.zeros(1, x.size(0), hidden_size)
# 입력 x와 초기 은닉 상태 h0를 RNN에 통과시켜 출력(out)과 마지막 은닉 상태를 반환
out, _ = self.rnn(x, h0)
# RNN의 출력인 모든 시간 단계에 대해 완전 연결층을 적용해 최종 출력 생성
out = self.fc(out)
# 최종 출력값을 반환
return out
# 모델 초기화
input_size = 1
hidden_size = 32
output_size = 1
model = SimpleRNN(input_size, hidden_size, output_size) # SimpleRNN 클래스의 인스턴스 생성
# 손실 함수와 최적화 알고리즘 정의
criterion = nn.MSELoss() # 손실 함수 정의: 평균 제곱 오차(MSE)를 사용하여 예측값과 실제값 사이의 오차를 계산
optimizer = optim.Adam(model.parameters(), lr=0.01) # 최적화 알고리즘 정의: Adam 옵티마이저 사용, 학습률(lr)은 0.01
# 모델 학습
num_epochs = 100 # 전체 데이터셋을 100번 반복 학습 (에포크 수)
for epoch in range(num_epochs):
outputs = model(X) # 입력 데이터를 모델에 통과시켜 예측 값(outputs) 생성
optimizer.zero_grad() # 이전 배치의 기울기를 초기화
loss = criterion(outputs, y) # 예측 값과 실제 레이블 간 손실 계산
loss.backward() # 역전파를 통해 각 파라미터에 대한 기울기 계산
optimizer.step() # 기울기를 바탕으로 가중치 업데이트 (파라미터 최적화)
# 매 10 에포크마다 손실 값을 출력하여 학습 상황을 모니터링
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}') # 현재 에포크, 전체 에포크 수, 손실 값을 출력
print('Finished Training') # 모든 에포크 학습 완료 후 메시지 출력LSTM
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
# 데이터 생성 및 전처리
# Sine 파형 데이터 생성
def create_sine_wave_data(seq_length, num_samples):
X = [] # 입력 시퀀스를 저장할 리스트
y = [] # 출력 시퀀스를 저장할 리스트
for _ in range(num_samples):
start = np.random.rand() # 0과 1 사이의 임의의 시작점을 생성
x = np.linspace(start, start + 2 * np.pi, seq_length) # 시작점부터 2파이 만큼의 범위를 seq_length 개수만큼 균등하게 나눔
X.append(np.sin(x)) # 입력 시퀀스로 사인 값을 추가
y.append(np.sin(x + 0.1)) # 출력 시퀀스로 입력 시퀀스를 약간 이동시킨 사인 값을 추가 (예측할 목표값)
return np.array(X), np.array(y) # 입력과 출력 시퀀스를 NumPy 배열로 반환
seq_length = 50 # 각 시퀀스의 길이 (50개의 시점 데이터)
num_samples = 1000 # 생성할 샘플의 총 개수
X, y = create_sine_wave_data(seq_length, num_samples) # Sine 파형 데이터 생성
# 데이터셋을 PyTorch 텐서로 변환
X = torch.tensor(X, dtype=torch.float32).unsqueeze(-1) # NumPy 배열을 PyTorch 텐서로 변환하고, 마지막 차원에 추가하여 (batch_size, seq_length, 1) 형태로 만듦
y = torch.tensor(y, dtype=torch.float32).unsqueeze(-1) # 위와 같당
# 간단한 LSTM 모델 정의
# SimpleLSTM 클래스 정의
class SimpleLSTM(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleLSTM, self).__init__()
self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True) # LSTM 레이어 정의: 입력 크기, 은닉 상태 크기, batch_first=True는 입력 텐서의 배치 크기가 첫 번째 차원임을 의미함
self.fc = nn.Linear(hidden_size, output_size) # 완전 연결 층 정의: 은닉 상태 크기에서 출력 크기로 변환
def forward(self, x):
h0 = torch.zeros(1, x.size(0), hidden_size) # 초기 은닉 상태 정의: (num_layers, batch_size, hidden_size)
c0 = torch.zeros(1, x.size(0), hidden_size) # 초기 셀 상태 정의: (num_layers, batch_size, hidden_size)
out, _ = self.lstm(x, (h0, c0)) # 입력 x와 초기 은닉 상태 (h0, c0)를 LSTM에 통과시켜 출력과 마지막 은닉 상태를 반환
out = self.fc(out)
return out
# LSTM 모델 초기화
input_size = 1
hidden_size = 32
output_size = 1
model = SimpleLSTM(input_size, hidden_size, output_size) # SimpleLSTM 클래스의 인스턴스 생성
# 손실 함수와 최적화 알고리즘 정의
criterion = nn.MSELoss() # 손실 함수 정의: 평균 제곱 오차(MSE)를 사용하여 예측값과 실제값 사이의 오차를 계산
optimizer = optim.Adam(model.parameters(), lr=0.01) # 최적화 알고리즘 정의: Adam 옵티마이저 사용, 학습률(lr)은 0.01
# 모델 학습
num_epochs = 100 # 전체 데이터셋을 100번 반복 학습 (에포크 수)
for epoch in range(num_epochs):
outputs = model(X) # 입력 데이터를 모델에 통과시켜 예측 값(outputs) 생성
optimizer.zero_grad() # 이전 배치의 기울기를 초기화
loss = criterion(outputs, y) # 예측 값과 실제 레이블 간 손실 계산
loss.backward() # 역전파를 통해 각 파라미터에 대한 기울기 계산
optimizer.step() # 기울기를 바탕으로 가중치 업데이트 (파라미터 최적화)
# 매 10 에포크마다 손실 값을 출력하여 학습 상황을 모니터링
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}') # 현재 에포크, 전체 에포크 수, 손실 값을 출력
print('Finished Training') # 모든 에포크 학습 완료 후 메시지 출력모델평가시각화
# 모델 평가
model.eval() # 모델 평가 모드로 전환 (Dropout 등의 레이어가 있는 경우 비활성화됨)
with torch.no_grad(): # 평가 단계에서는 기울기를 계산하지 않음 (메모리 절약 및 속도 향상)
predicted = model(X).detach().numpy() # 모델을 사용하여 예측하고, 텐서를 NumPy 배열로 변환
# 시각화
plt.figure(figsize=(10, 5)) # 그래프의 크기 설정
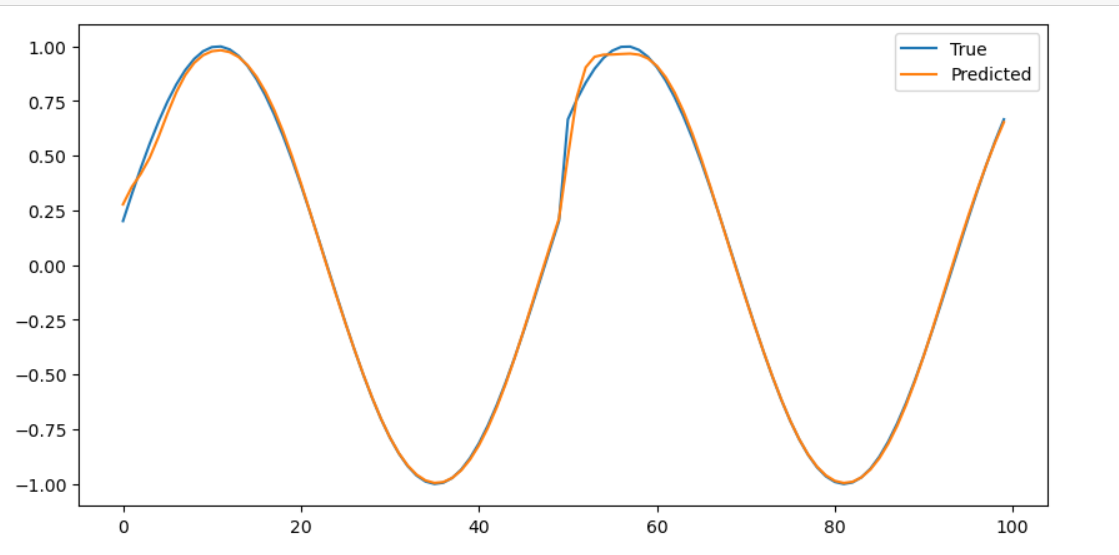
plt.plot(y.numpy().flatten()[:100], label='True') # 실제값을 시각화 (첫 100개 샘플)
plt.plot(predicted.flatten()[:100], label='Predicted') # 예측값을 시각화 (첫 100개 샘플)
plt.legend() # 범례 추가
plt.show() # 그래프 출력이런식으로 나온다.
딥러닝의 주요 세가지 모델을 공부해봤는데 완벽하게 아는건 아직 무리다.
아직 이해보다 반복
