실습 주피터 노트북 양식으로 보기 링크

Linear Regression 기본 개념

선형 회귀(Linear Regression)는 두 개 이상의 변수 간의 관계를 선형 방정식으로 모델링하는 통계적 기법이다. 이 방법을 통해 독립 변수(X)와 종속 변수(y) 사이의 관계를 설명하거나 예측할 수 있다.

기본 개념

• 선형 회귀는 독립 변수(X)와 종속 변수(y) 사이에 직선의 관계가 있다고 가정한다.
• 목표는 독립 변수(X)의 변화에 따라 종속 변수(y)가 어떻게 변하는지 최적의 직선을 찾는 것이다. 이 직선은 데이터 점들과 가장 잘 맞도록 설정된 선으로, 오차(잔차)를 최소화하는 선이다.

수학적 표현

선형 회귀는 다음과 같은 수학적 공식으로 표현된다:

y = wX + b

• ( y ): 예측 값(종속 변수)
• ( X ): 입력 값(독립 변수)
• ( w ): 가중치(weight), 입력 변수의 기울기
• ( b ): 편향(bias) 또는 절편(intercept), 직선이 y축과 만나는 지점

목표

선형 회귀의 목표는 데이터 포인트들과의 차이(즉, 예측 값과 실제 값 간의 차이)를 최소화하는 ( w )와 ( b )를 찾는 것이다. 이는 최소제곱법 (Least Squares Method)을 통해 최적의 가중치와 편향을 찾는 방식으로 구현된다.

예시

예를 들어, 공부 시간(X)이 주어졌을 때 그에 따른 시험 성적(y)을 예측한다고 가정해 보자. 여기서 선형 회귀는 데이터에 가장 적합한 직선을 찾고, 주어진 크기에 따라 시험 성적을 예측하는 데 사용된다.

종류

1. 단순 선형 회귀 (Simple Linear Regression):
   • 하나의 독립 변수(X)와 하나의 종속 변수(y) 간의 관계를 모델링함.
2. 다중 선형 회귀 (Multiple Linear Regression):
   • 여러 개의 독립 변수(X1, X2, X3, ...)와 하나의 종속 변수(y) 간의 관계를 모델링함.

용도

• 예측: 미래의 값을 예측하는 데 사용된다. 예를 들어, 집 값, 주식 가격 등.
• 설명: 독립 변수와 종속 변수 간의 관계를 설명하고 분석하는 데 사용된다.

손실 함수

선형 회귀에서 모델의 성능을 측정하기 위해 손실 함수로 평균 제곱 오차 (Mean Squared Error, MSE)를 사용한다. MSE는 예측 값과 실제 값 간의 차이의 제곱의 평균을 계산하여 예측이 얼마나 정확한지 측정한다.

요약

• 선형 회귀(Linear Regression)는 독립 변수와 종속 변수 간의 선형 관계를 찾기 위한 통계적 방법이다.
• 기울기(w)와 절편(b)를 조정하여 최적의 직선을 찾아내는 것이 목표이다.
• 이를 통해 데이터 간의 관계를 모델링하고 예측할 수 있다.

선형 회귀는 데이터 분석과 예측에 있어 가장 기본적이고 중요한 기법 중 하나이다.

---

Linear Regression 실습

공부 시간에 따른 시험 점수

준비

import matplotlib.pyplot as plt
import pandas as pd 

먼저 필요한 라이브러리 불러오기.

dataset = pd.read_csv('LinearRegressionData.csv')

필요한 데이터셋 불러오기! 출처 : 나도코딩
같은 폴더에 미리 저장해뒀다 (링크타고가면 파일있닷.)

파일확인은 git-hub링크에서...

변수 지정

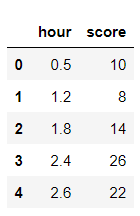
파일을 조금 살펴보면 시간과 점수가 있다.
선형회귀를 실습중이니, 이에 맞게 독립변수와 종속변수(결과)를 설정해서 이 관계를 학습시켜야 한다.

X = dataset.iloc[:, :-1].values # 처음부터 마지막 컬럼 직전까지의 데이터 (독립 변수)
y = dataset.iloc[:,-1].values # 마지막 컬럼 데이터 (종속변수 - 결과)

독립변수 (X)와 종속변수 (y)를 설정했다.

살펴보면 X는 공부시간, y는 이에따른 시험점수다.

코드도 조금 살펴보면 X의 값은 iloc을 사용해서 .values를 사용해 Numpy 2차원 배열로 반환하여 정의했다.y는 결과(종속변수)로 마지막 열을 가져와 Numpy 1차원 배열로 반환해서 정의했다.

X, y # X, y를 입력해보면

(array([[ 0.5],
        [ 1.2],
        [ 1.8],
        [ 2.4],
        [ 2.6],
        [ 3.2],
        [ 3.9],
        [ 4.4],
        [ 4.5],
        [ 5. ],
        [ 5.3],
        [ 5.8],
        [ 6. ],
        [ 6.1],
        [ 6.2],
        [ 6.9],
        [ 7.2],
        [ 8.4],
        [ 8.6],
        [10. ]]),
 array([ 10,   8,  14,  26,  22,  30,  42,  48,  38,  58,  60,  72,  62,
         68,  72,  58,  76,  86,  90, 100], dtype=int64))

이렇게 나타난다.

학습시키기

from sklearn.linear_model import LinearRegression  # 선형 회귀 모델을 위한 라이브러리 임포트
reg = LinearRegression()  # 선형 회귀 모델 객체 생성
reg.fit(X, y)  # 독립 변수(X)와 종속 변수(y)를 사용해 모델을 학습시킴

reg.fit(X, y)는 X와 y 데이터를 사용하여 모델을 학습시킨다. 모델은 가중치와 절편을 계산하여 최적의 직선을 찾아내게 된다.

y_pred = reg.predict(X) # X 에 대한 예측 값 출력
y_pred

y_pred는 X 에 대한 예측 값이다.
즉 예측된 종속 변수 값이다. 위에서 fit()을 통해 학습된 최적의 직선에 대해서!
y = mx + b 에서 X를 넣으면 예측될 y값이다.

시각화

plt.scatter(X, y, color='blue') # 산점도 그래프
plt.plot(X, y_pred, color='green') # 선 그래프 X를 넣었을때 예측되는 Y값을 넣기에 y_pred를 넣음
plt.title('Score by hours') # 제목
plt.xlabel('hours') # X 축 이름
plt.ylabel('score') # Y 축 이름
plt.show()

이렇게 나온 값들을 시각화 한번 해보자.

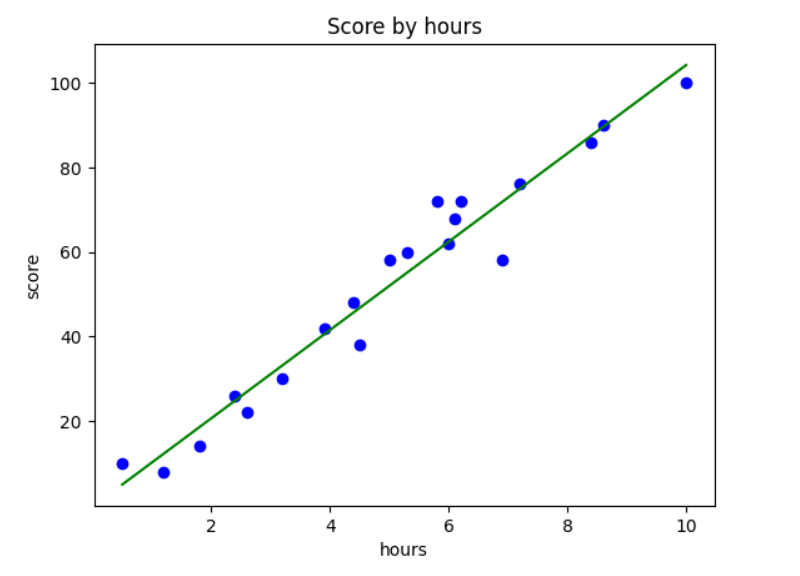
X값을 넣었을 때 예상되는 y_pred값이 그래프로 표현된다. ok

print('9,8,7시간 공부했을 때 예상 점수 : ', reg.predict([[9],[8],[7]])) # 2차원 배열 형태로 들어가서 [[]]

9,8,7시간 공부했을 때 예상 점수 :  [93.77478776 83.33109082 72.88739388]

reg.coef_ # 기울기 (m)구하기
reg.intercept_ # y 절편 (b)구하기

결과값:
array([10.44369694])
-0.218484702867201

즉 y = mx + b -> y = 10.4436x - 0.2184이란 일차함수로 나타낼 수 있다.

데이터 세트 분리

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state = 0)

설명:

• X_train: 학습용 독립 변수 데이터. 모델을 학습시키는 데 사용
• X_test: 테스트용 독립 변수 데이터. 학습된 모델의 성능을 평가할 때 사용
• y_train: 학습용 종속 변수 데이터. 학습 과정에서 모델이 예측하고자 하는 목표값
• y_test: 테스트용 종속 변수 데이터. 테스트 데이터의 예측 성능을 평가하기 위해 사용

요약

• train_test_split() 함수는 데이터를 학습용과 테스트용으로 랜덤하게 나누는 역할을 한다.
• test_size=0.2는 전체 데이터의 20%를 테스트 데이터로 사용한다는 의미이다.
• random_state=0를 설정하면 데이터셋을 분할할 때 항상 같은 방식으로 나누도록 해준다.
• 결과적으로 X_train, y_train은 모델을 훈련하는 데 사용하고, X_test, y_test는 모델의 일반화 성능을 평가하기 위해 사용한다.

데이터를 학습용과 테스트용으로 나누는 이유는 모델이 학습에 사용되지 않은 새로운 데이터를 얼마나 잘 예측할 수 있는지를 평가하기 위해서이다. 이를 통해 모델의 일반화 능력을 판단할 수 있으며, 과적합(overfitting)을 피하는 데도 도움을 준다.

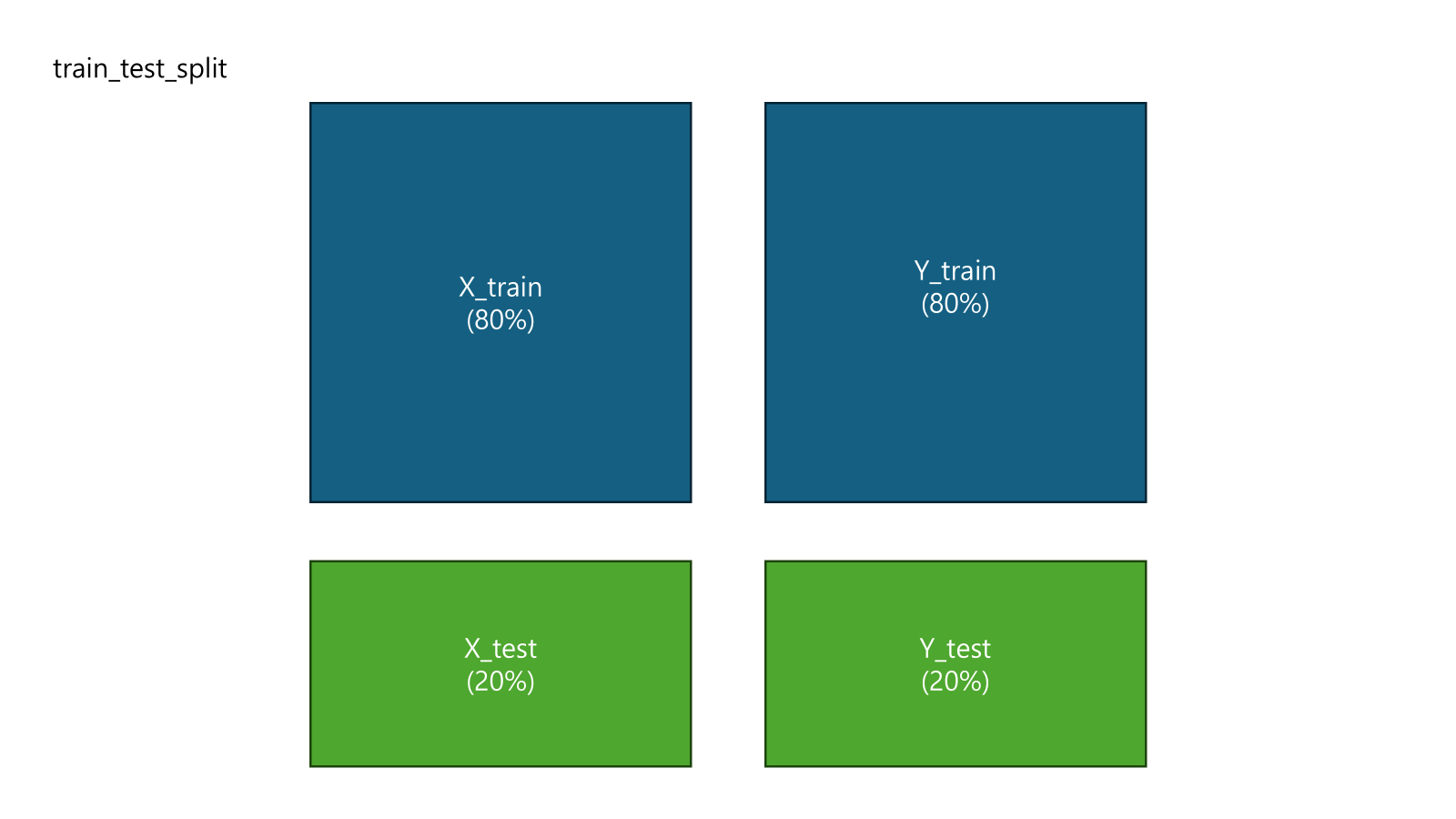
이렇게 있다고 이해하면 된다.

---

분리된 데이터를 통한 모델링

이제 훈련세트와 테스트세트를 이용해서 데이터 시각화까지 해보자.

from sklearn.linear_model import LinearRegression
reg = LinearRegression() # 다시 불러오고

reg.fit(X_train, y_train) # 훈련 세트로 학습해보자

reg.fit()을 이용해 X_train, y_train을 넣고 학습시킨다. (이전과 동일방법)

시각화
1. Train 세트 시각화

plt.scatter(X_train, y_train, color='blue') # 산점도 그래프
plt.plot(X_train, reg.predict(X_train), color='green') # 선 그래프 X를 넣었을때 예측되는 Y값을 넣기에 y_pred를 넣음
plt.title('Score by hours (train data)') # 제목
plt.xlabel('hours') # X 축 이름
plt.ylabel('score') # Y 축 이름
plt.show()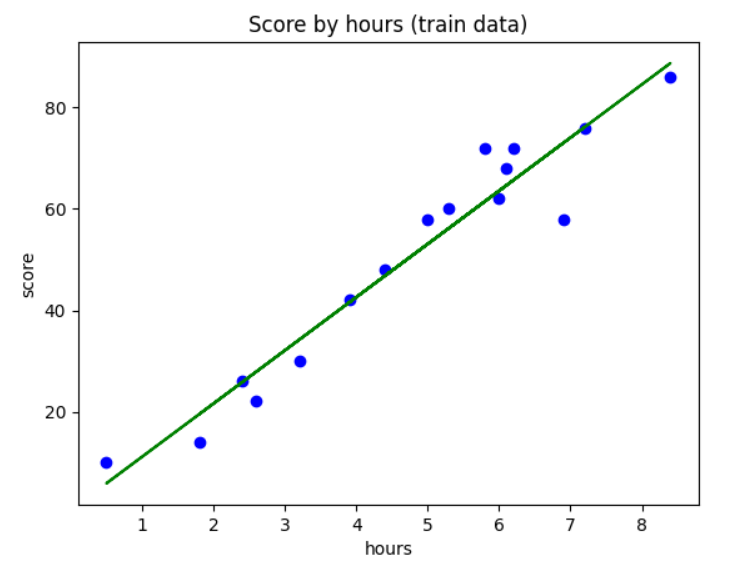

2. Test 세트 시각화

plt.scatter(X_test, y_test, color='blue') # 산점도 그래프
plt.plot(X_train, reg.predict(X_train), color='green') #
plt.title('Score by hours (test data)') # 제목
plt.xlabel('hours') # X 축 이름
plt.ylabel('score') # Y 축 이름
plt.show()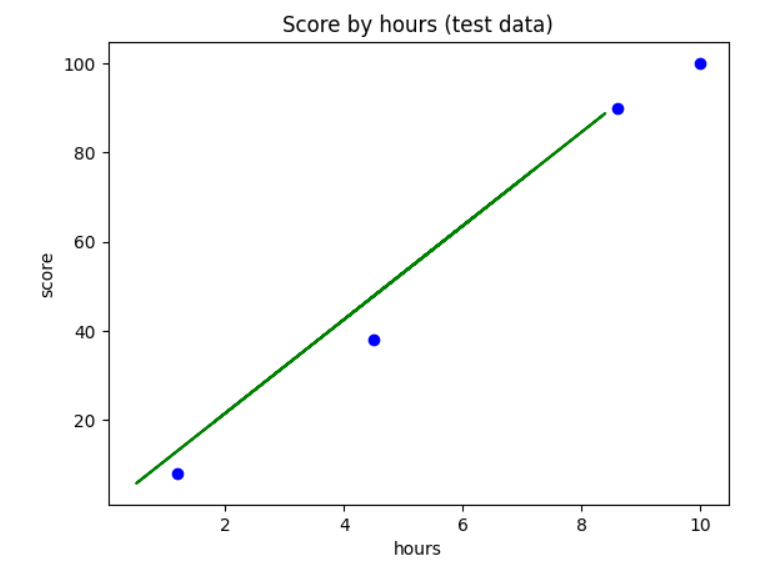

reg.coef_ # 기울기
reg.intercept_ # 절편

결과값
array([10.49161294])
0.6115562905169369

모델 평가

reg.score(X_test, y_test) # 테스트 세트를 통한 모델 평가 0~1 사이
reg.score(X_train, y_train) # 훈련 세트를 통한 모델 평가

결과값
0.9727616474310156
0.9356663661221668

지금은 데이터가 20개로 작아서 훈련세트가 테스트 세트보다 결과값이 좋지 않게 나왔다 ^^;

---

이렇게 머신러닝 기법중 하나인 선형 회귀(Linear Regression)의 기본 개념과 간단한 실습으로 훈련,테스트세트 나누기, 모델 시각화, 평가를 해봤다. 가장 처음 배우는 머신러닝이고 새로운 라이브러리도 사용해 보고 모르는 것들을 구글링하면서 이해하는 과정이 힘들지만 보람찼다... 한주간 고생했다.