[Paper Review] Neural Collaborative Filtering

이승규·2022년 7월 11일

Deep Learning Recommender System paper-review

Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, Tat-Seng Chua. 2017. Neural Collaborative Filtering. 2017 International World Wide Web Conference Committee

1. Introduction

추천 시스템은 이커머스, 온라인 뉴스나 소셜 미디어 사이트 등 많은 양의 정보가 있는 산업에서 필요한 정보만을 추출해주는 데에 중추적인 역할을 수행하고 있다. 대표적인 추천 시스템으로 유저와 아이템 간의 과거 상호작용을 토대로 개인화된 추천을 해주는 collaborative filtering 방식이 있는데, 그 중에서도 matrix factorization(MF)이 가장 잘 알려져 있다. MF는 유저와 아이템을 latent space로 투영시켜 latent feature에 대한 벡터로 각각을 나타낸다. 그리고 유저와 아이템의 상호작용을 나타내기 위해 latent 벡터 간의 inner product를 이용한다.

이렇게 만들어진 MF는 latent factor를 잡아낸 효과적인 model-based 추천 시스템이지만, 유저와 아이템 간의 상호작용을 간단하게 inner product로만 나타냈다는 점에서 한계가 존재한다. 단순히 latent feature들을 선형적으로 결합하는 것은 복잡한 상호작용을 잡아내기에 충분하지 않다는 것이다.

본 논문에서는 Deep Neural Networks(DNN)의 non-linearity를 이용해 유저의 implicit feedback signal을 잡아내는 방법을 다룬다. 나아가 MF가 Neural Collaborative Filtering(NCF)의 특수한 케이스임을 보이고 NCF의 효율성을 실험을 통해 증명한다. 여기서 implicit feedback이란 영상을 시청하거나 상품을 구매하고 아이템을 클릭하는 것처럼 유저의 행동에서 나타나는 선호도를 의미한다. implicit feedback은 자동으로 트래킹되고 content providers들이 쉽게 수집할 수 있는 데이터이지만 비정형 데이터이기 때문에 활용하기엔 까다롭다는 특징이 있다.

2. Preliminaries

2.1 Learning from Implicit Data

유저 수를 $M$ , 아이템 수를 $N$ 이라고 하면, 유저의 implicit feedback으로부터 user-item interaction matrix $\text{Y} \in \mathbb{R}^{M \times N}$ 을 다음과 같이 정의할 수 있다.

y_{ui} = \begin{cases} 1, \text{ if interaction (user }u \text{, item }i \text{) is observed; }\\ 0, \text{ otherwise.}\ \end{cases}

$y_{ui}$ 가 1이면 유저 $u$ 와 아이템 $i$ 간에 상호작용이 존재하는 것을 의미한다. 하지만 그렇다고 해서 $u$ 가 $i$ 를 선호한다는 뜻은 아니다. 비슷하게, $y_{ui}$ 가 0이라고 해서 유저 $u$ 가 $i$ 를 선호하지 않는다고 말할 순 없다. 단순히 유저가 그 아이템에 관심이 없을 수도 있는 것이다.

결국 implicit feedback을 통한 추천은 $\text{Y}$ 에서 관찰되지 않은 요소들을 추정하는 문제가 된다. 이를 수식으로 표현하면 $\hat{y}_{ui} =f(u, i | \Theta)$ 이 되고, 여기서 $\hat{y}_{ui}$ 는 상호작용 $y_{ui}$ 에 대한 예측값, $\Theta$ 는 모델 파라미터, $f$ 는 interaction function을 의미한다.

파라미터 $\Theta$ 를 추정하기 위해, 흔히 두 가지 목적 함수를 이용한다. 바로 pointwise loss와 pairwise loss이다. pointwise loss는 회귀 문제에서 자주 사용되는 함수로 타겟 $y_{ui}$ 와 예측값 $\hat{y}_{ui}$ 의 squared loss를 최소화하는 것이다. 반면 pairwise loss는 관찰된 $y$ 값이 관찰되지 않은 값보다 더 큰 값을 갖도록 하여 둘 사이의 margin을 최대화하는 함수이다.

본 논문에서 NCF는 $\hat{y}_{ui}$ 를 추정하기 위한 interaction function $f$ 로 neural network를 사용하여, pointwise와 pairwise 둘을 모두 이용할 수 있다.

2.2 Matrix Factorization

MF는 각각의 유저와 아이템을 latent feature들의 실수 벡터로 나타낸다. 예를 들어 유저 $u$ 와 아이템 $i$ 의 latent vector를 $\mathbf{p}_u$ 와 $\mathbf{q}_u$ 라고 하면 MF는 둘 사이의 interaction $y_{ui}$ 을 다음과 같이 추정한다.

\hat{y}_{ui} = f(u, i | \mathbf{p}_u , \mathbf{q}_i) = \mathbf{p}^T_u \mathbf{q}_i = \sum_{k=1}^K{p_{uk} q_{ik}}

식을 보면 알 수 있듯이 MF는 latent factor들의 선형 결합으로 만들어진 linear model이다. 다만 linear model이기에 발생하는 한계점이 존재한다.

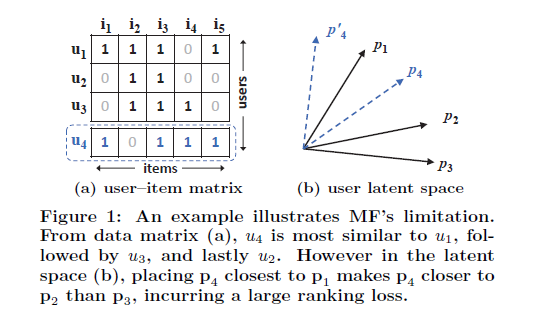
위 그림 (a)에서 두 유저 $i$ , $j$ 사이의 유사도 $s_{ij}$ 를 Jaccard coefficient를 이용해 계산하면, $s_{23}(0.66)>s_{12}(0.5)>s_{13}(0.4)$ 순으로 높다. 이를 latent space 상에 기하학적으로 나타낸 결과가 (b)의 $\mathbf{p}_1$ , $\mathbf{p}_2$ , $\mathbf{p}_3$ 이다. 그런데 어떤 새로운 유저 $u_4$ 가 들어왔을 때, 기존 유저들과의 유사도를 계산하면 $s_{41}(0.6)>s_{43}(0.4)>s_{42}(0.2)$ 순으로 높지만 새로운 벡터 $\mathbf{p}_4$ 를 $\mathbf{p}_1$ 과 가장 가깝고 $\mathbf{p}_2$ 보다는 $\mathbf{p}_3$ 에 가깝게 배치하려면 모순이 생긴다.

이는 MF가 복잡한 유저-아이템 interaction을 저차원의 latent space 상에서 표현하기 때문에 발생하는 문제이다. latent factor의 차원 $K$ 를 키우면 해결이 될 것이라 생각할 수도 있지만 오히려 overfitting 문제가 발생할 가능성이 크다. 따라서 저자는 이 한계를 극복하기 위해 non-linear한 DNN을 도입한다.

3. Neural Collaborative Filtering

3.1 General Framework

유저-아이템 interaction $y_{ui}$ 를 잡아내기 위해, 저자는 아래 그림과 같은 multi-layer representation을 이용했다.

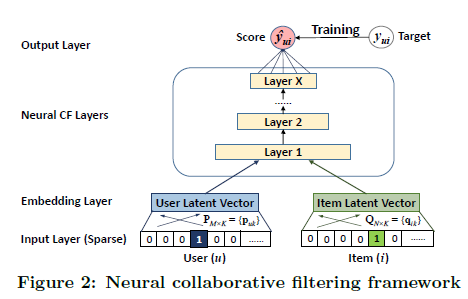
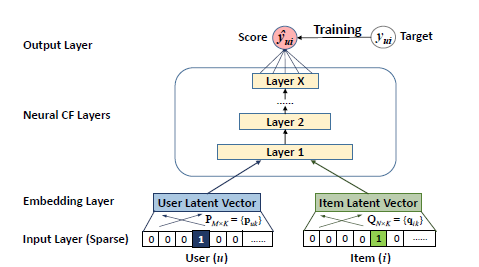
기본적으로 한 layer의 output이 다음 layer의 input으로 들어가는 구조로 설계되어 있다. 가장 먼저 bottom layer의 input으로는 유저 $u$ 와 아이템 $i$ 에 대해 one-hot encoding된 벡터 $\mathbf{v}_u^U$ , $\mathbf{v}_i^I$ 가 들어간다.

input layer 바로 위에는 embedding layer가 있는데, embedding layer은 fully connected layer로써 sparse한 input을 dense vector로 변환시켜주는 역할을 한다. 이렇게 만들어진 dense vector가 바로 latent vector라고 할 수 있다.

이어서 유저와 아이템의 embedding vector는 multi-layer neural architecture를 통과한다. neural collaborative filtering layers라고 명명된 이 layer들을 통과하면서 latent vector는 prediction score $\hat{y}_{ui}$ 로 변환된다.

이 과정을 수식으로 표현하면 다음과 같다.

\hat{y}_{ui} = f(\mathbf{P}^T \mathbf{v}_u^U , \mathbf{Q}^T \mathbf{v}_i^I | \mathbf{P}, \mathbf{Q}, \Theta _f)

식에서 $\mathbf{P} \in \mathbb{R}^{M \times K}$ , $\mathbf{Q} \in \mathbb{R}^{N \times K}$ 는 latent factor matrix이고 $\Theta_f$ 는 interaction function $f$ 의 모델 파라미터이다. interaction function은 아래와 같은 식으로 나타낼 수 있는데,

f(\mathbf{P}^T \mathbf{v}_u^U , \mathbf{Q}^T \mathbf{v}_i^I) = \phi_{out} (\phi_X (... \phi_2(\phi_1 (\mathbf{P}^T \mathbf{v}_u^U , \mathbf{Q}^T \mathbf{v}_i^I))...))

$\phi_{out}$ 과 $\phi_{x}$ 는 각각 output layer와 $x$ 번째 layer의 mapping function을 의미한다.

모델에서 output $\hat{y}_{ui}$ 는 0에서 1 사이의 값을 갖고, 타겟값 ${y}_{ui}$ 는 0 또는 1의 값을 갖는다. ${y}_{ui}=1$ 인 interaction의 집합을 $\mathcal{Y}$ , ${y}_{ui}=0$ 인 interaction의 집합을 $\mathcal{Y}^-$ 라고 할 때 likelihood function은 다음과 같다.

p(\mathcal{Y}, \mathcal{Y}^- |\mathbf{P}, \mathbf{Q}, \Theta_f) = \prod_{(u, i) \in \mathcal{Y}} \hat{y}_{ui} \prod_{(u, i) \in \mathcal{Y^-}} (1- \hat{y}_{ui})

따라서 모델 학습을 위한 loss function은 양변에 -log를 취해주면 아래와 같은 형태가 된다.

L = - \sum_{(u, i) \in \mathcal{Y}} \text{log}\, \hat{y}_{ui} - \sum_{(u, i) \in \mathcal{Y}^-} \text{log}( 1- \hat{y}_{ui})\\ \qquad \qquad = - \sum_{(u, i) \in \mathcal{Y} \cup \mathcal{Y}^-} y_{ui}\, \text{log} \, \hat{y}_{ui} +(1-y_{ui})\text{log}(1-\hat{y}_{ui})

NCF는 위 binary cross-entropy 형태의 objective function을 최소화하는 방향으로 학습을 진행하며, 이때 stochastic gradient descent 방식으로 optimization이 수행된다.

3.2 Generalized Matrix Factorization(GMF)

우리가 기존에 알고 있던 MF는 NCF의 특수 케이스로 볼 수 있다. 논문에서는 다음과 같은 방법으로 이를 증명한다.

유저 latent 벡터 $\mathbf{p}_u$ 를 $\mathbf{P}^T \mathbf{v}_u^U$ 라고 하고, 아이템 latent 벡터 $\mathbf{q}_i$ 를 $\mathbf{Q}^T \mathbf{v}_i^I$ 라고 하자. NCF의 첫 번째 layer 함수를 다음과 같이 정의한다.

\phi_1 (\mathbf{p}_u, \mathbf{q}_i) = \mathbf{p}_u \odot \mathbf{q}_i

$\odot$ 은 벡터간의 element-wise product를 의미한다.

그럼 최종적으로 얻어지는 $\hat{y}_{ui}$ 는 아래 식을 따른다.

\hat{y}_{ui} = a_{out} (\mathbf{h}^T (\mathbf{p}_u \odot \mathbf{q}_i))

만약 activation function $a_{out}$ 을 identity function으로, output layer의 edge weight $\mathbf{h}$ 를 1로만 이루어진 단위벡터로 본다면, 결국 이는 MF 모델이 된다.

NCF framework 상에서 MF는 쉽게 확장되고 일반될 수 있다. 이를 Generalized MF로 이름 붙였으며, $a_{out}$ 에는 sigmoid 함수 $\sigma (x) = 1/(1+e^{-x} )$ 를 두었고 $\mathbf{h}$ 는 앞선 log loss를 통해 얻은 가중치로 두었다.

3.3 Multi-Layer Perceptron(MLP)

유저 벡터와 아이템 벡터를 단순히 concatenate 하는 것은 유저와 아이템 간의 복잡한 interaction을 설명하기에 충분하지 않다. 이를 해결하기 위해 저자는 concatenated vector에 hidden layer를 쌓는 MLP 구조를 이용해 모델의 flexibility와 non-linearity를 보장해주고 element-wise product만을 이용하는 GMF의 한계를 보완했다.

MLP 모델의 구조를 구체적으로 표현하면 다음과 같다.

\mathbf{z}_1 = \phi_1 (\mathbf{p}_u, \mathbf{q}_i) = \begin{bmatrix} \mathbf{p}_u \\ \mathbf{q}_i \end{bmatrix},

\phi_2(\mathbf{z}_1) = a_2 (\mathbf{W}_2^T \mathbf{z}_1 +\mathbf{b}_2),

\cdots \cdots

\phi_L(\mathbf{z}_{L-1}) = a_L (\mathbf{W}_L^T \mathbf{z}_{L-1} +\mathbf{b}_L),

\hat{y}_{ui} = \sigma(\mathbf{h}^T \phi_L(\mathbf{z}_{L-1}))

식에서 $\mathbf{W}_x,$ $\mathbf{b}_x ,$ $a_x$ 는 각각 가중치 행렬, bias 벡터, 활성화 함수를 의미한다. 활성화 함수는 실험적으로 가장 좋은 성능을 보인 ReLU를 이용했다.

NN 구조는 tower pattern을 이용했는데, tower pattern이란 bottom layer에 가장 노드 수를 많이 두고 점차 노드 수를 줄여나간 형태를 말한다. 이런 구조에서 모델은 data의 abstractive feature를 더 잘 학습할 수 있다.

3.4 Fusion of GMF and MLP

지금까지의 내용을 정리하면, GMF는 linear kernel을 이용해서 latent feature interaction을 학습하고, MLP는 non-linear kernel로 interaction을 학습한다.

저자는 이 두 모델을 합쳐 각 모델이 가진 장점을 살리고자 했다. 우선 GMF와 MLP가 학습할 embedding을 분리해주고 모델이 학습된 후 마지막 hidden layer를 통과하며 도출된 결과를 concatenate하도록 아래 사진과 같은 구조를 설계했다.

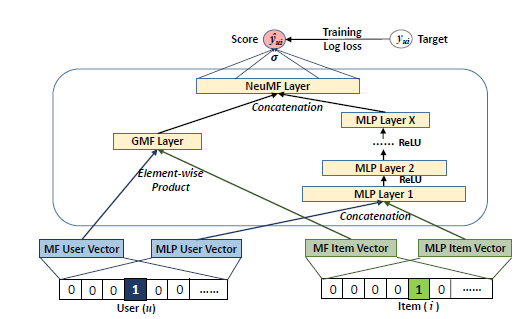
이를 수식으로 표현하면 다음과 같다.

\phi^{GMF} = \mathbf{p}_u^G \odot \mathbf{q}_i^G ,

\phi^{MLP} = a_L (\mathbf{W}_L^T (a_{L-1}( \cdots a_2 (\mathbf{W}_2^T \begin{bmatrix} \mathbf{p}_u^M \\ \mathbf{q}_i^M \end{bmatrix}+b_2 ) \cdots)) + b_L) ,

\hat{y}_{ui} = \sigma(\mathbf{h}^T \begin{bmatrix} \phi^{GMF} \\ \phi^{MLP} \end{bmatrix})

$\mathbf{p}_u^G$ 와 $\mathbf{p}_u^M$ 은 각각 GMF와 MLP의 유저 embedding, $\mathbf{q}_i^G$ 와 $\mathbf{q}_i^M$ 은 각각 GMF와 MLP의 아이템 embedding을 나타낸다. 앞서 언급했듯이 MLP의 활성화 함수로는 ReLU를 이용했다.

이렇게 만들어진 Neural Matrix Factorization(NeuMF) 모델은 MF의 linearity와 DNN의 non-linearity가 결합되어 유저-아이템 latent structure를 잘 학습했고 HR@10과 NDCG@10을 이용해 기존 모델과 비교했을 때 더 좋은 성능을 보였다.

Neural Collaborative Filtering은 papers with code 사이트에서 Recommendation Systems를 검색했을 때(https://paperswithcode.com/task/recommendation-systems) 가장 많이 implemented 되었다고 나오는 논문이다. 그만큼 딥러닝을 이용한 추천시스템의 기초가 된 논문이라고 할 수 있는데, 생각보다 어렵지 않고 아이디어가 간단해서 읽기 좋았다.