preview

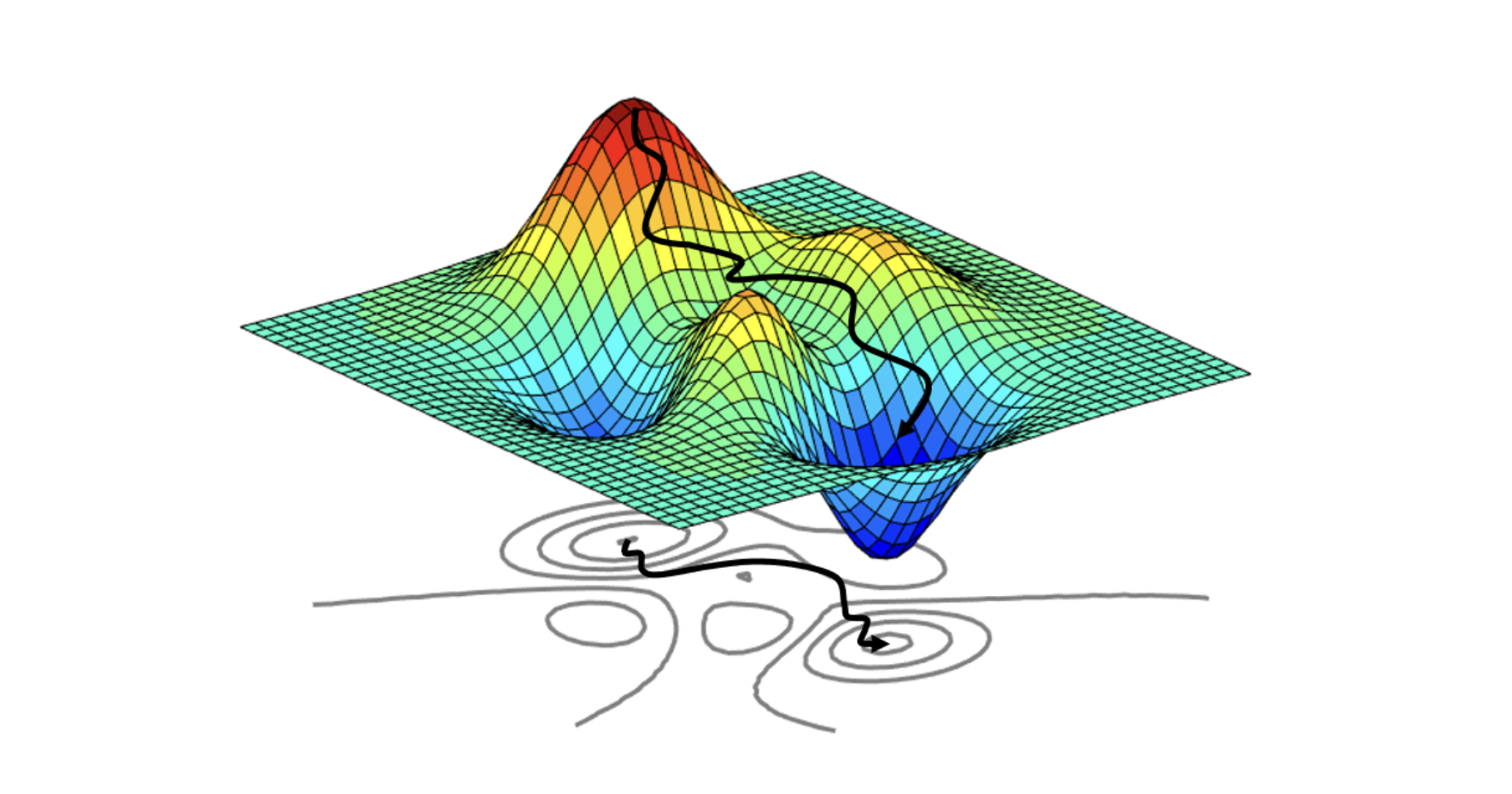
이전 장에서 신경망에 대해 알아봤다면 이번에는 신경망 학습의 목적인 최적화를 알아볼 것이다.

---

최적화란?

최적화란?
신경망 학습의 목적은 손실 함수의 값을 가능한 낮추는 매개변수(parameter)를 찾는 것이다.
즉, 어떤 목적함수의 값을 최적화시키는 파라미터 조합을 찾는 것을 뜻한다.
더 간단하게 얘기하면 손실함수의 극대, 극소지점이 되는 파라미터를 찾는 것이다!

최적화의 중요개념!

👉 우리가 공부하게될 개념은 아래와 같다

• 일반화(generalization)
• 오버피팅(over-fitting) & 언더피팅(under-fitting)
• 편향과 분산의 트레이드오프(Bias-variance tradeoff)
• 교차 검증(Cross validation)
• 경사하강법(Gradient descent)
• 정규화(regularization)
• 부스트스트래핑(Bootstrapping)과 배깅과 부스팅(Bagging and boosting)

👉 벌써 보기만 해도 머리 아픈 많은 개념이 머리 속에 뒤죽박죽 섞여있다.
👉 우리가 공부할 내용들은 각각 개념을 차례차례 공부하면 개념들은 이해가 가지만 왜 이걸 해야하는지 감이 오지 않는다.
👉 좀 더 직관적인 이해를 위해 해당 개념들을 일반화를 기준으로 왜 해당 개념들이 필요한지를 정리해보겠다.

---

일반화(Generalization)

👉 일반화란 학습된 모델이 새로운 데이터에 대해 얼마나 잘 작동하는 지를 의미한다
👉 최적화를 위해서는 모델이 일반화(generalization) 되어야한다.
👉 아래에 설명할 개념들은 다 모델을 일반화 시키기 위한 개념들이라고 생각하면 된다.

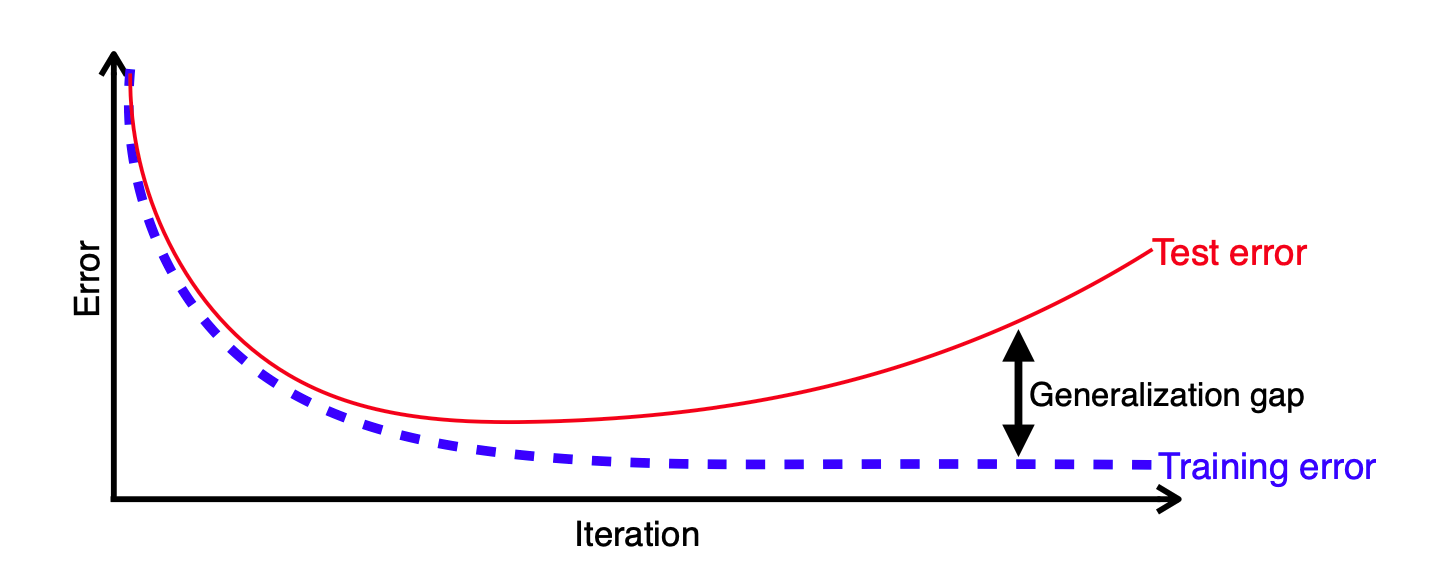
👉 결국 최적화란 모델을 과소적합(under-fitting)없이 학습을 잘 시키고, 과대적합(over-fitting)이 아닌 새로운 데이터에도 잘 작동하도록 없이 일반화(generalization) 시키는 것이다.

---

over-fitting VS under-fitting

👉 최적화를 위해서는 과대적합과 과소적합 사이에서 최적화된 절충점을 찾아 모델을 만드는 것이 매우 중요하다

과대적합 (over-fitting)
모델이 학습 데이터에 대한 정확한 예측을 하지만 새로운 데이터에 대해서는 정확한 예측을 하지 못하는 경우 이다. 모델은 학습데이터를 기반으로 새로운 데이터에 대한 결과를 예측하기 때문에 학습데이터를 과하게 학습한 경우 발생한다

과소적합(under-fitting)
모델이 입력데이터와 출력데이터 간 유의미한 관계를 확인할 수 없을 때 발생하는 오류로, 학습 데이터를 제대로 학습하지 않았을 때 발생한다

over-fitting vs under-fitting
1. 과소적합은 학습데이터와 테스트데이터에 대해 모두 부정확한 결과를 제공하므로 편향성이 높다
2. 반면에 과대적합은 학습데이터에 대해서는 정확한 결과를 제공하지만 테스트데이터에 대해서는 정확한 결과를 제공하지 않음으로 높은 분산을 가지고 있다

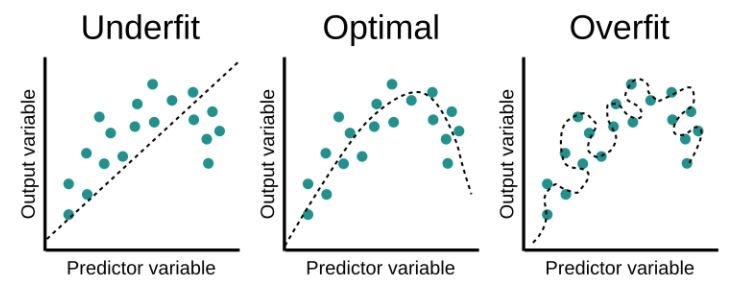
👉 이제 과대적합과 과소적합이 무엇인지는 알았는데, 어떻게 과대적합인지 과소적합인지를 판단해야될까?
👉 그 방법론은 교차검증(Cross-validation)과, 편향과 분산의 트레이드오프(Bias-variance tradeoff)로 알 수 있다

---

편향과 분산의 트레이드오프(Bias-variance tradeoff)

👉 편향과 분산은 공부하며 자주 듣던 개념이지만 트레이트오프란 무슨 뜻일까?

tradeoff : 한쪽이 커지면 다른 한쪽은 줄어드는 상충관계로 하나가 증가하면 다른 하나는 무조건 감소한다는 뜻이다.

👉 트레이트오프란 뜻을 알았다면 Bias-variance tradeoff은 다음과 같음을 알 수 있다.

Bias-variance tradeoff
모델이 학습 데이터의 범위를 넘어서 지나치게 일반화하는 것을 예방하기 위해 오차를 최소화 할때 겪는 문제이다.
즉, 편향이 커지면 분산이 감소하고, 분산이 커지면 편향이 감소한다.

👉 우리가 최소화하려는 손실함수는 아래와 같이 편향, 분산, 노이즈로 분해 될 수 있다

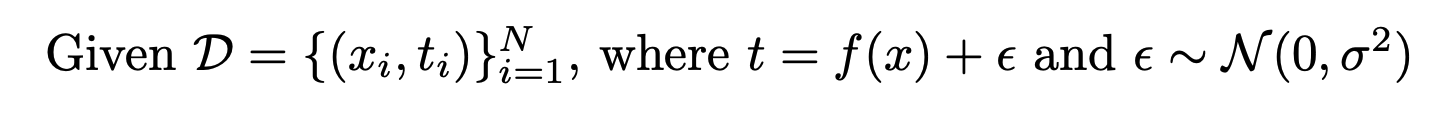
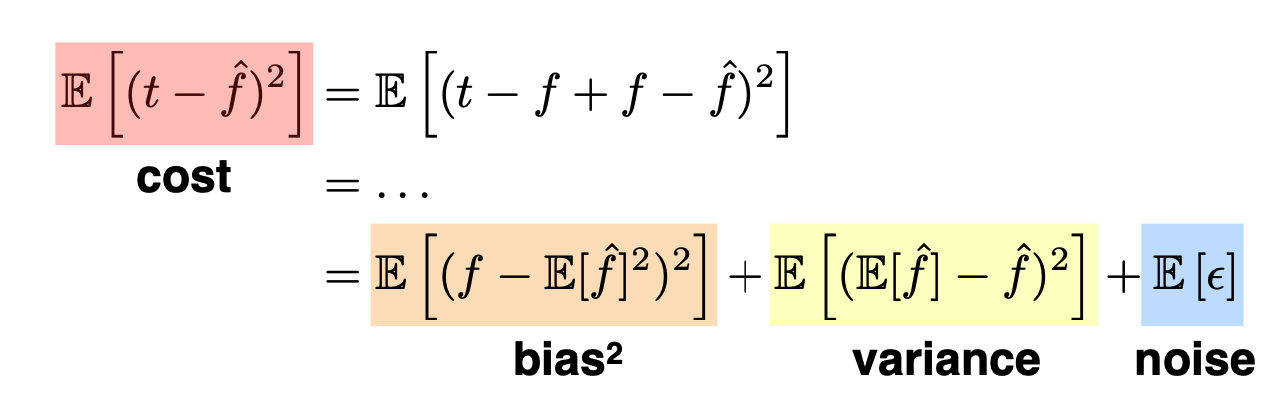
👉 Bias-variance tradeoff는 우리가 최소화하려는 손실함수를 편향, 분산으로 분해해 학습을 얼마나 시켜야할지 생각해보기 위한 방법이라고 생각하면 된다.

• 편향 : 모델에서 잘못된 가정을 했을 때 발생하는 오차로, 높은 편향을 가지면 모델이 학습데이터로 부터 멀어지고 모델을 지나치게 단순화 시켜 데이터의 특징과 결과물 사이의 적절한 관계를 놓지는 과소적합 문제를 발생시킨다. 편향은 우리가 학습데이터를 바꿈에 따라 모델의 평균 정확도가 얼마나 많이 변하는지 보여준다

• 분산 : 학습 데이터에 내재된 작은 변동 때문에 발생하는 오차로, 높은 분산값은 큰 노이즈까지 모델링에 포함시키는 과적합을 발생시킨다. 즉, 실제 현상과 관계없는 것까지 학습되는 경향을 나타낸다. 분산은 특정 입력 데이터에 대해 모델이 얼마나 민감한지를 나타낸다.

• 노이즈 : 줄일 수 없는 불가피한 오차로 보통 일상생활에서 발생하는 불가피한 오류를 얘기한다. 평균이 0,분산이 $\sigma ^{2}$ 인 정규 분포이다.

---

Cross-validation(교차검증)

Cross-validation
교차 검증은 모델이 독립적인 데이터 세트로 일반화되는 방식을 평가하기 위한 모델 검증 기술이다.
즉, 테스트 데이터 세트에 대해 정확한 결과를 제공하는지를 평가하는 것이다

👉 해당 방법은 주로 과대적합을 확인할 때 사용한다
👉 교차 검증에도 다양한 방법이 있지만 그건 추후에 포스팅 하겠다!

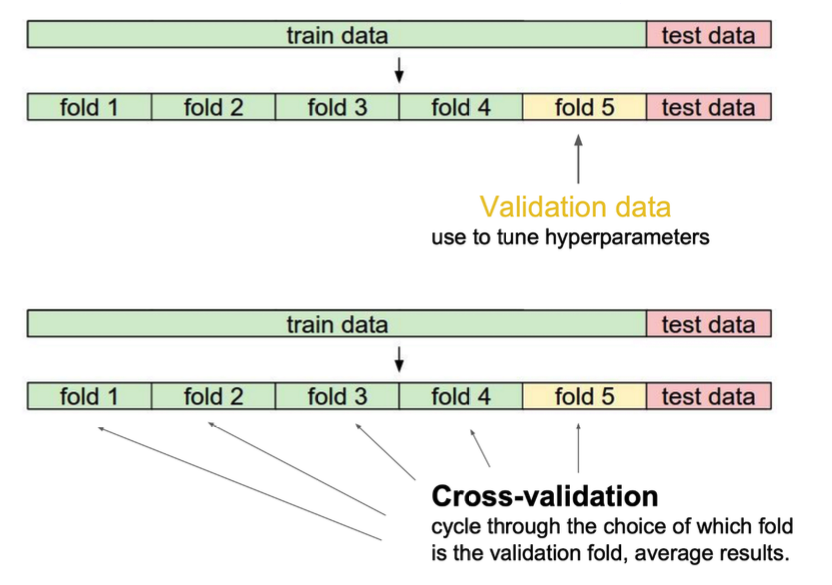
👉 우리는 교차 검증과, 편향과분산의 트레이트 오프로 과대 적합인지 과소 적합인지를 판단하는 법을 알게되었다.

Summary

👉 그렇다면 우리는 해당 문제를 해결하기 위해한 다음과 같은 질문을 얻을 수 있다.

🆀 만약 과소 적합인 경우 어떻게 학습을 시켜야 더 빠르게 최적의 적합으로 갈 수 있을까?
🅰 더 빠르게 적합할 수 있는 경사하강방법을 선택하자!

🆀 만약 과대 적합이라면 어떻게 학습데이터에만 국한 되지 않도록 일반화를 해야할까? 규제를 가하면 어떨까?
🅰 과대 적합이 되지 않도록 규제(penalty)를 가하는 정규화(regularization)방법을 알아보자!

🆀 만약 최적의 적합을 찾기 위해 하나의 모델이 아닌 여러가지 모델을 사용하면 어떻까?
🅰 앙상블 기법인 배깅과 부스팅을 알아보자!

👉 해당 질문들을 토대로 서로 헷갈리는 여러 개념들을 나만의 방식으로 아래와 같이 정리해보았다.

모델의 최적화란 모델의 일반화를 위한 최적의 parameter를 찾는 것!

일반화를 위한 방법론

• 오버피팅/언더피팅을 피하는 방법
  ➡️ 오버피팅/언더피팅 확인방법
  ➡️ 정규화(오버피팅/언더피팅 피하고 최적의 학습을 하는 방법론)

• 소량의 데이터 또는 분류가 어려운 데이터일 경우
  ➡️ 데이터 증량 방법
  ➡️ 하나의 모델이 아닌 여러 모델로 학습하는 방법(앙상블기법)

• 학습속도를 빠르게 하기 위한 방법
  ➡️ 여러 경사하강법

Epilogue

다음 장에서는 최적화를 위한 방법론들을 하나씩 소개해주겠다.

- 참고 -

• 네이버 부스트캠프 AITech 5rl
• 편향-분산 트레이드오프