경사하강법(Gradient descent)

Gradient descent
미분 가능 함수의 로컬 최소값을 찾기 위한 1차 반복 최적화 알고리즘입니다.
즉. 손실함수값이 낮아지는 방향으로 가기 위해 1차 미분계수를 이용하는 알고리즘이다

👉 경사하강법에서 우리가 결정해야 할 것은 다음과 같다

• 배치사이즈
• 스텝방향
• 스텝사이즈

배치사이즈에 따른 경사하강법

Batch gradient descent
👉 전체 데이터에서 계산된 그래디언트로 업데이트합니다.
👉 기존의 Gradient Descent 방식은 내가 가진 데이터를 다 넣어서 미분값을 계산하다보니 계산량이 많아 학습이 오래걸린다는 문제점이 있다

🆀 그렇다면 기존 Gradient Descent 방식보다 더 빠른 방법이 있을까?
🅰 모든 데이터의 미분값을 구하지 말고 일부 데이터로만 계산해보자

SGD(Stochastic gradient descent)
👉 추출된 데이터 한개에 대해서 계산된 기울기로 업데이트 한다

MGS(Mini-batch gradient descent)
👉 전체 데이터 중 일부 샘플에 대해 계산된 기울기로 업데이트 한다

🆀 SGD와 MGS는 어떤 차이가 있을까?
👉 공통점

• 계산량이 줄어 기존 Gradient Descent 방식보다 빠르게 전진한다.
• 일부 샘플만 계산하니 기존 Gradient Descent 방식 보단 헤맨다
• 헤매니 스텝사이즈(학습률)에 따라 보폭이 낮으면 학습이 오래걸리고, 너무 크면 최적의 값을 찾기 못한다

👉 차이점

• SGD는 데이터가 1개 이므로 배치사이즈가 1이다. 그래서 계산은 매우 빠르지만 연산량이 너무 적어 GPU를 제대로 쓰지 못한다.
• 또한 하나의 데이터만 사용하기 때문에 최적값의 수렴하지 않을 가능성이 높다(수렴 안정성 낮음)
• 이를 보완하기 위해 하나의 데이터가 아닌 일부 샘플(미니배치)를 사용하여 경사하강법을 진행해 계산량은 줄이면서 최적의 값을 수렴한다

💁‍♀️ 대부분 SGD을 사용할때 하나의 데이터가 아닌 미니배치를 사용하므로 Mini-batch gradient descent를 SGD라고 부른다

경사하강시 배치사이즈가 주는 영향

🆀 계산량을 줄이면서 최적의 값의 수렴하기 위해 Mini-batch를 얼마만큼 하는 게 좋을까?
🅰 큰 배치사이즈보단 작은 배치사이즈가 최적의 값으로 수렴하기 좋다

On Large-batch Training for Deep Learning: Generalization Gap and Sharp Minima, 2017

• "It has been observed in practice that when using a larger batch there is a degradation in the quality of the model, as measured by its ability to generalize."
  "실제로 더 큰 배치를 사용할 때 일반화 능력으로 측정할 때 모델의 품질이 저하되는 것이 관찰되었습니다."
• "We ... present numerical evidence that supports the view that large batch methods tend to converge to sharp minimizers of the training and testing functions. In contrast, small-batch methods consistently converge to flat minimizers... this is due to the inherent noise in the gradient estimation."
  "우리는 ... 대규모 배치 방법이 훈련 및 테스트 기능의 예리한 최소화로 수렴되는 경향이 있다는 견해를 뒷받침하는 수치적 증거를 제시합니다. 반대로 소규모 배치 방법은 일관되게 평면 최소화로 수렴합니다... 이것은 고유한 그래디언트 추정에 노이즈가 있습니다."

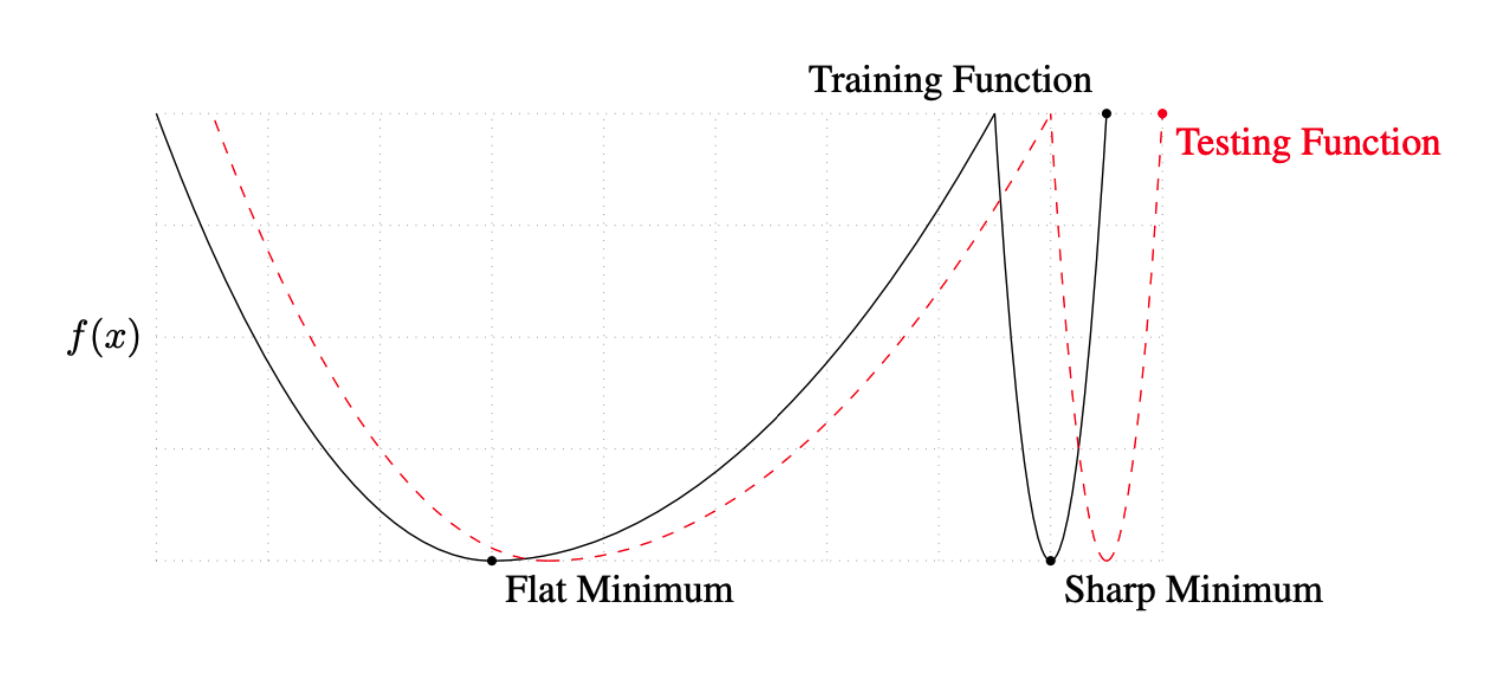
👉 결론 : 배치사이즈를 작게 가져가야 평평한 최소화로 수렴되므로 모델의 예측력이 더 좋다

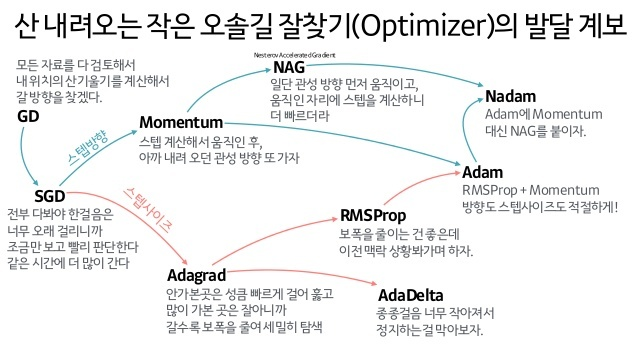
step방법에 따른 경사하강법

🆀 배치사이즈를 구했으니 스텝방향과 스텝사이즈는 어떻게 하는게 좋을까?

스텝방향을 조정해보자!

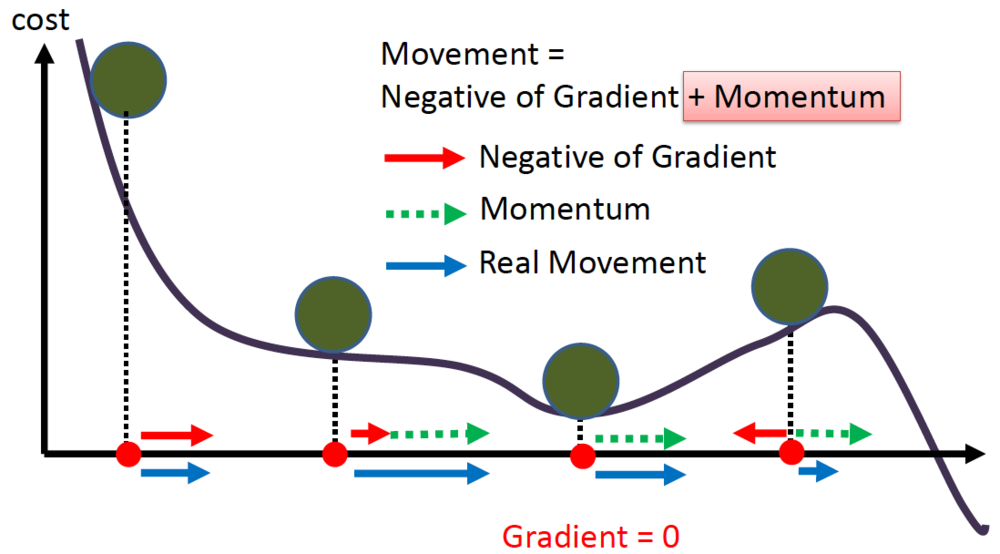
• Momentum
• Nesterov accelerated gradient

스텝사이즈를 조정해보자!

• Adagrad
• Adadelta
• RMSprop

스텝방향과 스텝사이즈 둘다 조정해보는건 어떨까!

• Adam
• Nadam

• 일반적인 경사하강법의 가중치 조정식

  

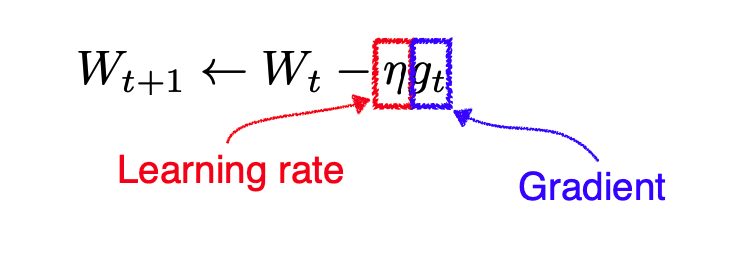
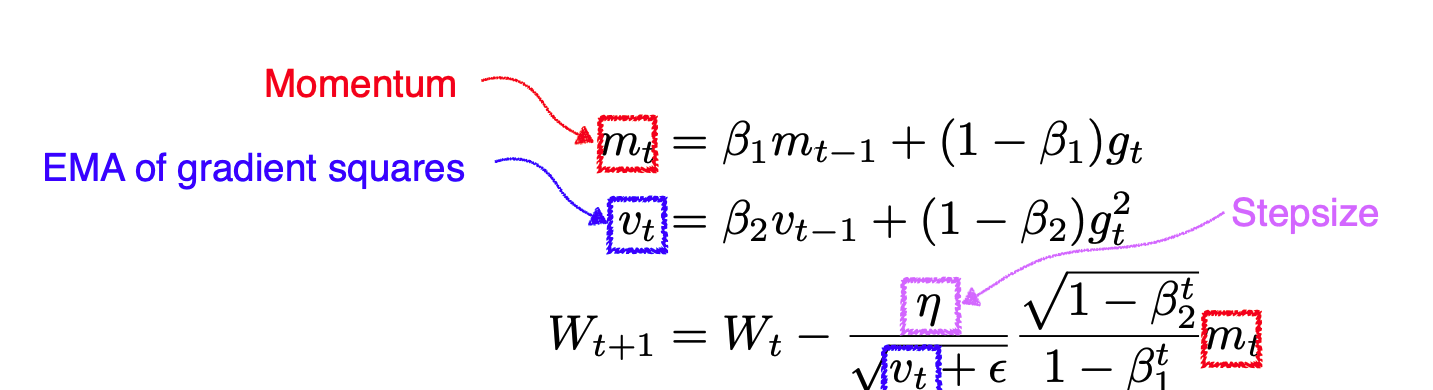
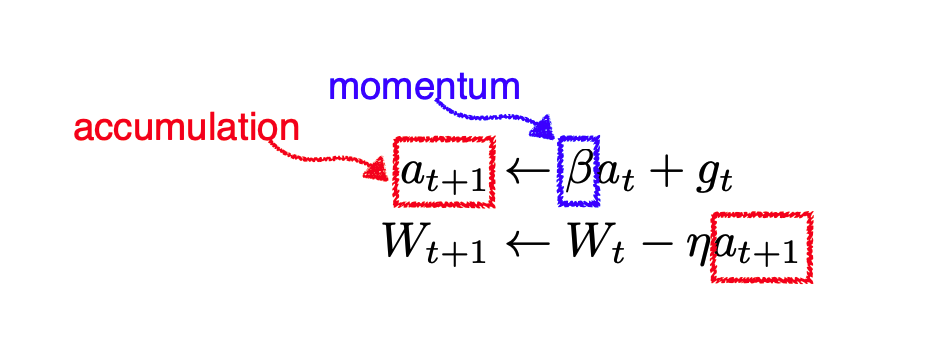
Momentum

• Momentum의 가중치 조정식

  

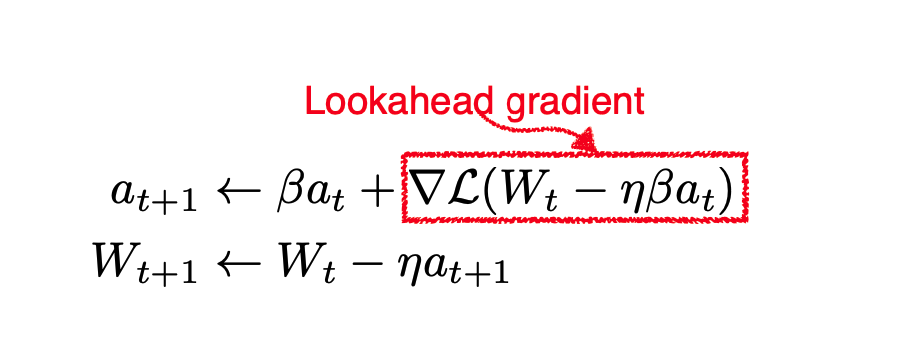
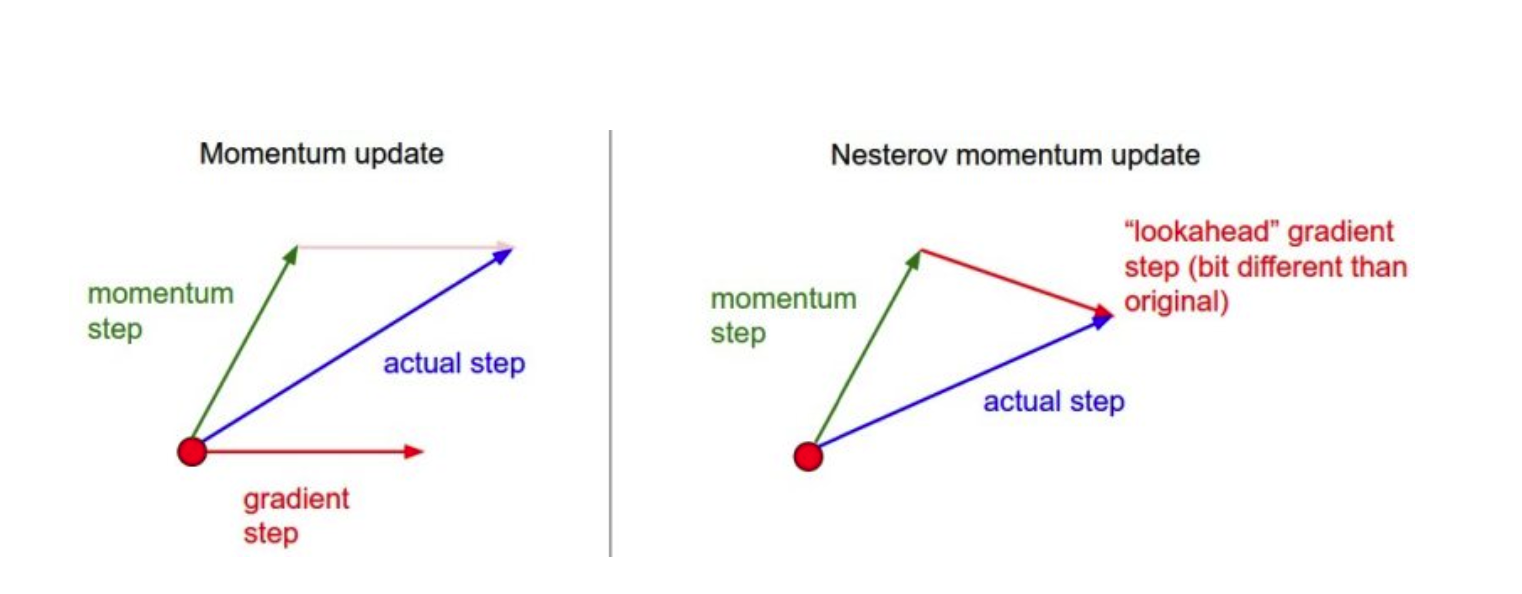
NAG

• Nesterov accelerated gradient의 가중치 조정식

  

Adagrad

• Adagrad는 학습 속도를 조정하여 간헐적인 매개변수에 대해 더 큰 업데이트를 수행하고 빈번한 매개변수에 대해 더 작은 업데이트를 수행합니다

  

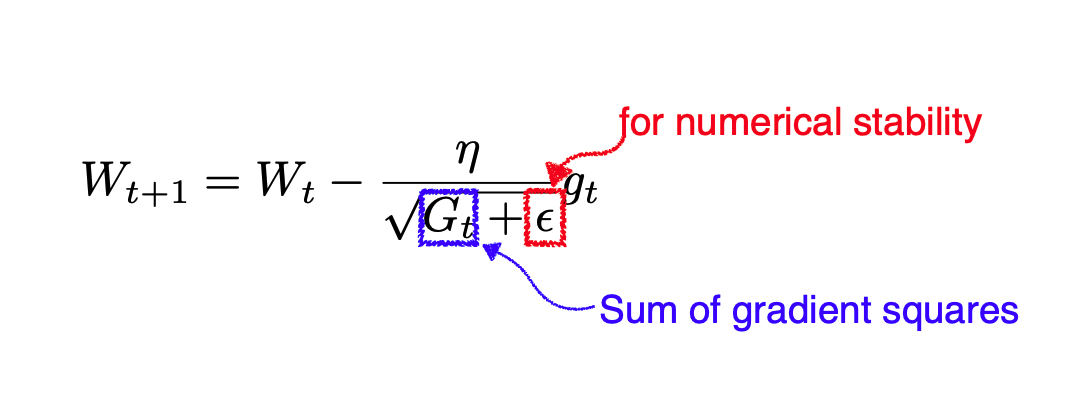
💁‍♀️ Adagrad로 교육이 장기간 진행되면 어떻게 될까?

Adadelta

• Adadelta는 Adagrad를 확장하여 누적 창을 제한하여 학습률을 단조롭게 감소시킵니다.
• Adadelta은 학습률이 없음

  

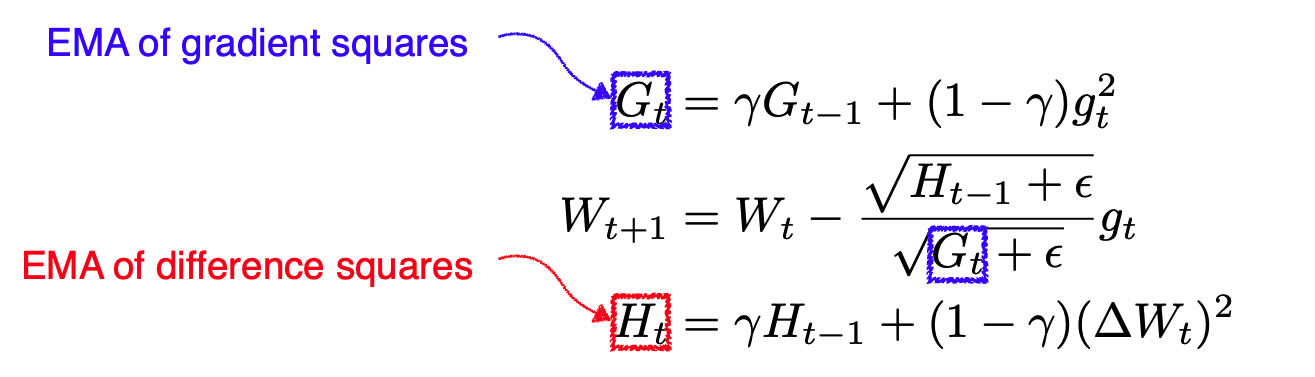
RMSprop

RMSprop은 Geoff Hinton이 강의에서 제안한 미공개 적응형 학습률 방법입니다.
RMSprop is an unpublished, adaptive learning rate method proposed by Geoff Hinton in his lecture.

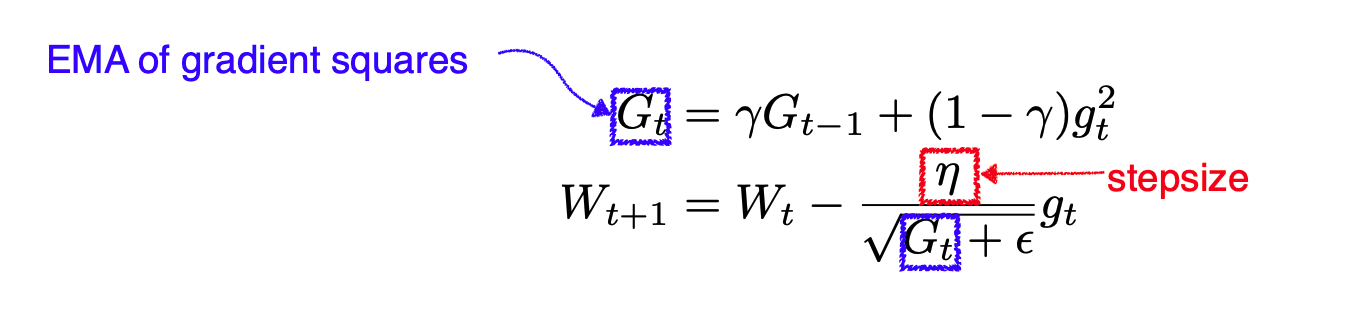
adam

Adaptive Moment Estimation (Adam) leverages both past gradients and squared gradients.
Adaptive Moment Estimation(Adam)은 과거 그래디언트와 제곱 그래디언트를 모두 활용합니다.

• Adam은 모멘텀을 적응형 학습 속도 접근 방식과 효과적으로 결합합니다.