📃 paper: https://arxiv.org/pdf/2012.09699.pdf
💻 code: https://github.com/graphdeeplearning/graphtransformer

NLP분야에서 뛰어난 성능을 거둔 Transformer는 다른 분야에도 활발하게 응용되고 있다. (ex: COMET , VIT) 이번에는 Graph 분야에 transformer를 적용한 논문에 리뷰해보려 한다.

✨ 임의의 그래프를 다룰 수 있는 일반화된 Graph transformer model을 제안하였다.

(Generalization : Training data, input data가 달라져도 출력에 대한 모델의 성능 차이가 나지 않도록 하는 것)

Problem

• Graph의 sparsity한 특성을 어떻게 다룰 것인가?

• 그래프에서의 노드의 위치를 어떤 Positional encoding기법을 사용하여 representation할 것인가?

Graph sparsity

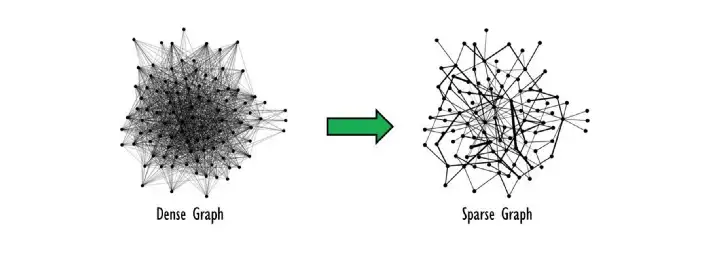
sparsity 는 graph를 학습하는데 있어서 great inductive bias가 될 수 있다. Graph가 sparsity하다는 것은 노드와 노드 사이의 간선이 별로 없다는 뜻이다. (반대는 Dense graph)
Graph neural network 측면에서 바라보자면, original transformer에서는 모든 단어들은 attention 과정을 통하여 'fully connected graph of words'가 된다. 왜 이러한 방식을 선택을 하였을까? 그 이유는
첫째, 문장의 단어들 사이에서 의미있는 interaction이나 connection을 찾기 어렵기 때문이다.
둘째, nlp transformer에서 다루는 단어들은 그래프 적으로 표현하면 수십 혹은 수백 노드보다 작은 수준이기 때문에 fully connected여도 연산이 가능하기 때문이다.

그러나 Graph dataset의 경우에는 arbitrary connectivity structre(즉, edge)를 사용할 수 있고 node size는 수백만 혹은 수십억개에 달한다. 따라서 graph에 기존의 transformer에서 사용하던 attention방식을 그대로 사용하는 것은 불가능하거나 매우 비효율적일 것이다.

Positional Encoding

NLP에서의 transformer는 각 단어 토큰이 전체 sequence에서 어디에 위치해 있는지와 단어 사이의 거리 정보를 전달할 수 있는 positional encoding을 사용했다.

Graph에서 노드의 unique한 position을 고안한다는 것은 매우 어려운 일이다. 그래프가 symmetric하다면, 각 노드의 canonical position을 부여하는 것은 매우 어려운 일이다. 따라서 지금까지 GNN에서는 Graph 학습에서 node의 position에 invariant한 노드의 구조적 정보를 학습하도록 훈련되어왔다.
그렇다면 Graph에서는 node의 위치 정보를 어떻게 부여할 수 있을까?

Method

overview

1. the attention mechanism is a function of the neighborhood connectivity for each node in the graph.
2. the positional encoding is represented by the Laplacian eigenvectors
3. the layer normalization is replaced by a batch normalization layer(faster training, better generalization performance)
4. the architecture is extended to edge feature representation

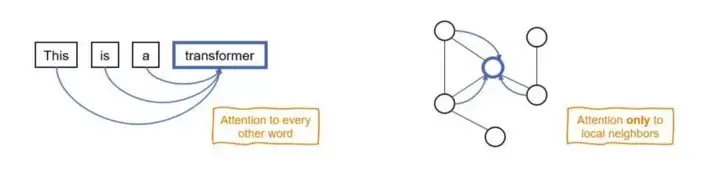
1. Node attends to local node neighbors

GNN에서 노드의 이웃 노드들의 정보를 합하여 해당 노드의 representation을 구하는 것 처럼, 이웃 노드 끼리만 attention을 진행한다. (similar to Graph Attention Networks) 이러한 방식이 더 실현가능성이 있고 sparse한 구조 정보를 활용하기에 더 유리하다고 한다.

2. Use Laplacian eigenvectors for positional encoding

최근의 선행 연구에서 Graph의 positional information을 사용한 결과 훨씬 몇 가지 task에서 훨씬 더 좋은 성능을 냈다는 결과가 있다. 이 논문에서는 Dwivedi et al.(2020) 논문에서 사전에 계산된 Laplacian eigenvectors를 노드의 위치 정보로 사용한 방식을 따랐다고 한다.

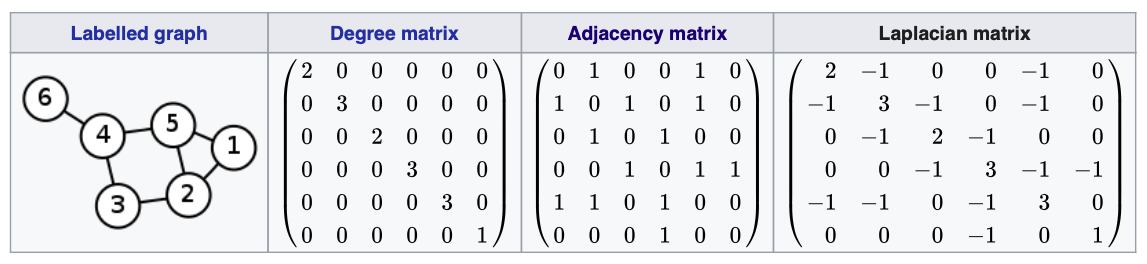
라플라시안 메트릭스는 Degree matrix에서 Adjacency matrix를 뺀 것이다. 실전에서는 symmetric normalrized laplacian matrix를 주로 사용하는데, 본 논문에서도 normalized 한 것을 사용했다.

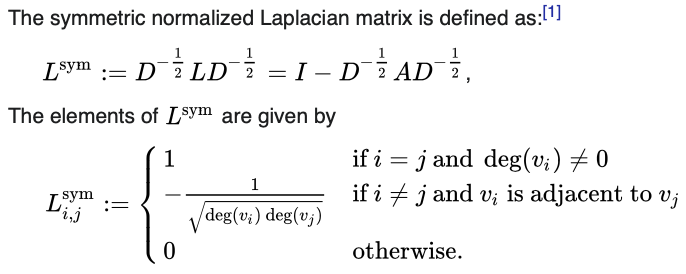
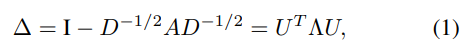
위의 symmetric normalrized Laplacian matrix에서 Eigenvalues($\Lambda$)와 Eigenvectors($U$) 가 정의된다. 노드의 positional encoding으로 노드의 $k$ smallest nontrivial eigenvectors 를 사용하였다 (denoted by $\lambda_i$). 이러한 방식을 똥해 distance-aware information 즉, 가까운 노드는 비슷한 positional feature를 갖고 먼 노드는 비슷하지 않은 feature를 갖도록 인코딩 할 수 있다고 한다.

3. Graph Transformer Architecture

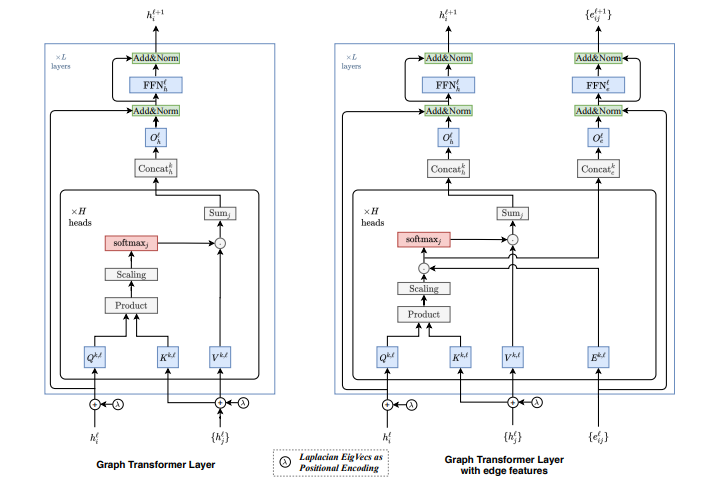
논문에서는 2가지의 모델 구조를 제안한다. 하나는 edge정보가 없는 그래프에 대한 구조이고, 다른 하나는 edge feature를 갖는 그래프에 대한 모델 구조이다.

Input

1) node feature $\alpha_i$ , edge feature $\beta_{ij}$ 는 각각 linear projection을 거쳐서 d 차원의 hidden feature $\hat h_i^0$, $e_{ij}^0$로 임베딩된다.

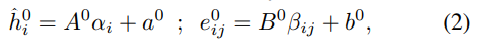
2) 미리 계산된 positional encoding 또한 linear projection을 거쳐서 d차원으로 임베딩된다. 그리고 node feature에 더한다. positional encoding은 input layer의 node feature에만 더해진다.

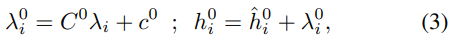
Graph Transformer Layer

edge 정보를 다루지 않는 모델의 layer부터 살펴보자(위 그림의 왼쪽 모델).

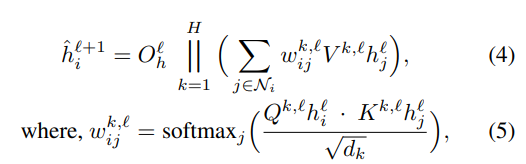
위의 식을 따라서 layer마다 값을 update 한다. 기존 transformer의 attention 과정과 흡사하다. $i$노드의 embedding에서 얻어진 쿼리와 $j$노드에서 얻어진 키값을 dot-product attention을 수행하여 어텐션 분포와 값을 구하고 멀티헤드 어텐션을 수행한다. $k$는 attention heads number 이고 || 는 concatenation을 의미한다.

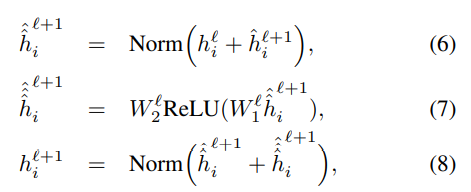
어텐션의 아웃풋 $\hat h_i^{l+1}$은 Feed Forward Network를 통과한 후 잔차연결과 정규화 과정을 거친다. 정규화는 LayerNorm 또는 BatchNorm을 사용한다.

Graph Transformer Layer with edge features

다음으로 edge feature를 사용하는 모델 구조를 살펴보자.

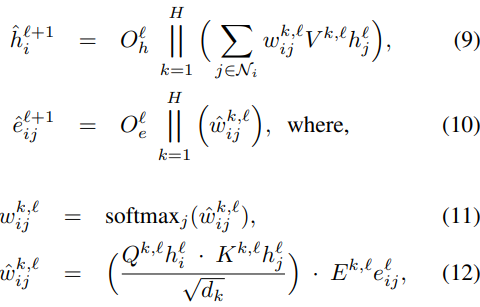
위의 오른쪽 모델 구조 그림에서 알 수 있듯이 softmax를 거치기 전의 attention score에 edge feature를 곱하고 모든 어텐션 헤드를 concate하여 edge attention output (10) 을 구한다. node attention output은 (12)를 softmax에 통과시킨 후 (11), 멀티헤드어텐션을 수행한다 (9).
두 가지 output $\hat h_i^{l+1}$과 $\hat e_{ij}^{l+1}$은 각각 Feed Forward Network를 통과한 후 잔차연결과 정규화 과정을 거친다.

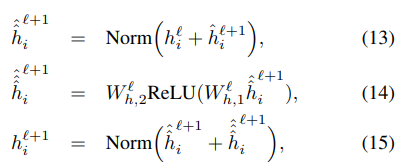
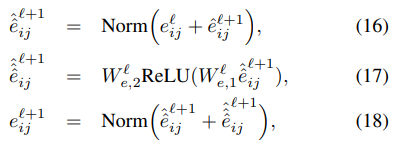
Experiments

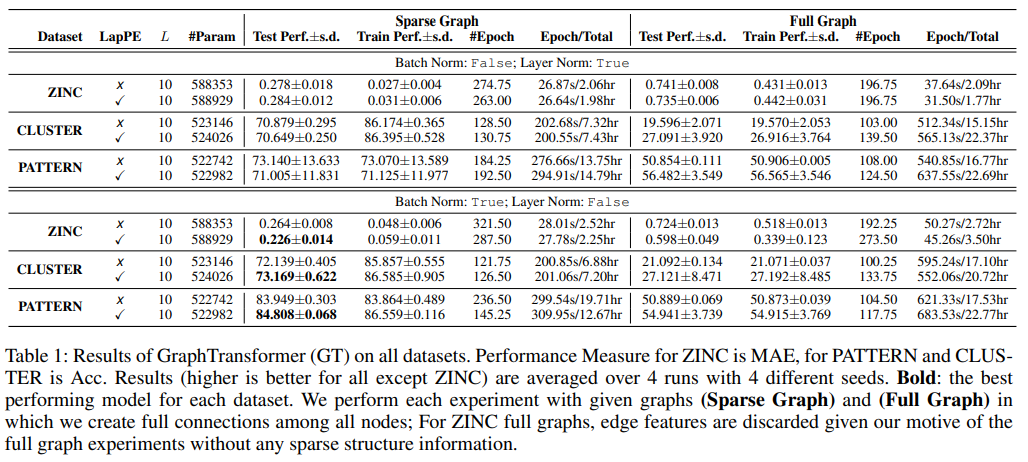
3가지 벤치마크에 대하여 Graph-Transformer의 성능을 평가하였다.

ZINC: molecular dataset, task of graph property regression, use 'Graph Transformer wirh edge features', metric: MAE.
PATTERN : task is classify the nodes into 2 communities. use 'Graph Transformer', metric: Acc.
CLUSTER : task is to assign a cluster label to each node.(6 labels, classificaition), use 'Graph Transfomer', metric: ACC.

Laplacian PE를 사용하고 Batch Norm을 했을 때 3가지 벤치마크 모두에서 성능이 가장 좋았다.
Full Graph 보다 Sparse Graph에서의 성능이 더 좋은 결과를 통해서 sparse graph connectivity가 중요한 inductive bias로 작용한다는 것을 알 수 있다.

GCN, GAT의 baseline모델보다 더 좋은 성능을 보였고 GatedGCN과 비교했을 때는 성능이 낮지만 큰 차이는 없다.
ZINC에 대해서 GatedGCN과 본 논문의 모델만 edge attribute를 사용하였다. 이 두가지와 다른 두 baseline을 비교했을 때, edge정보를 사용한 두 모델의 성능이 더 좋은 것을 확인할 수 있다.

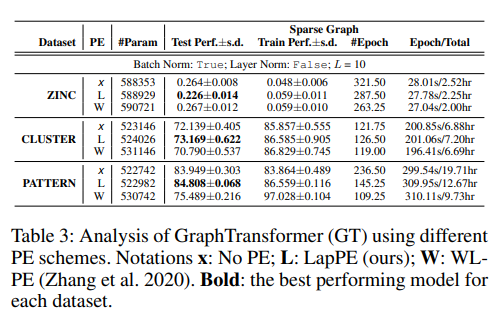
추가로 논문에서는 Laplacian eigenvectors가 PE로 사용하기에 적합한지 그 유용성을 실험하기 위해 Graph-BERT(Zhang et al.2020)에서 사용된 또 다른 PE방식과 그 성능을 비교하였다.

Graph-BERT에서는 모든 노드에 대한 Subgraph를 만든다.subgraph는 k+1개의 고정된 size를 갖는다.그리고 노드의 구조, 위치, 거리 정보를 사용하기 위하여 3가지의 node PE를 함께 사용한다. 1)Intimacy based relative, 2)Hop based relative distance encoding, 3)Weisfeiler Lehman based absolute PE.

본 실험에서는 Ablation analysis로 Laplacian PE 대신 WL-PE를 사용하여 비교를 진행하였다. 실험 결과 다른 PE를 사용했을 때보다 Laplacian PE를 사용했을 때의 성능이 더 좋음을 확인할 수 있다.

Contribution

• Graph에서 Sparsity한 성질이 중요한 inductive bias로 작용한다는 것을 밝혀냈다.
• Graph Transformer 구조에 Lapalacian PE를 사용하는 것이 좋다는 것을 보였고, layer norm 대신 Batch normalization을 사용하였다.
• 기존의 방식들을 잘 조합하여 simple하면서 generic한 graph transformer모델을 제안하였다.

---

이미지 출처
fig 1: https://data-science-blog.com/blog/2021/04/07/multi-head-attention-mechanism/
fig 2: https://blog.metaflow.fr/sparse-coding-a-simple-exploration-152a3c900a7c
fig 3: https://towardsdatascience.com/graph-transformer-generalization-of-transformers-to-graphs-ead2448cff8b