에라토스테네스의 체의 시간복잡도를 증명하기 위해 공부하다보니 테일러 급수에 대한 개념이 필요해서 포스팅을 하게 되었다.
테일러 급수와 테일러 정리란?
가령, 우리가 ∫01sin(x2)dx을 계산해야 한다고 가정해보자. 아마 쉽지 않을 것이다. 그러나, 다항함수의 급수로 이를 근사한 값은 구할 수 있다.
∫01sin(x2)dx=∫01(1!x2−3!x6+5!x10−⋯)dx
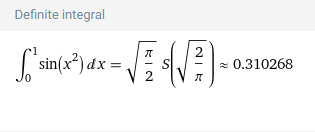
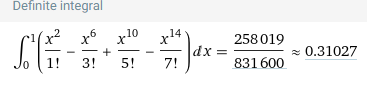
이때 다항함수가 아닌 함수를 다항함수로 표현하는 방법을 테일러 급수라 하며, 이를 통해 근사하는 행위를 테일러 정리라고 한다. 그리고 놀랍게도 근사한 값의 오차는 0에 수렴한다. 물론 항상 그런것이 아니다, 현재 예시는 적분범위가 [0,1]이기 때문에 이를 보장할 수 있다. 이에 관한 자세한 이야기는 나중에 라그랑주 나머지 정리를 통해 다뤄보겠다.
테일러 급수의 증명
지금부터 테일러 급수를 증명해보겠다. 증명은 FTC2(Fundamental Theroem of Calculus Part 2)로부터 시작된다.
∫axf′(t)dt=f(x)−f(a) 에서
∫ax1⋅f′(t)dt
=[(t−x)f′(t)]ax−∫ax(t−x)f′′(t)dt (증명을 위해 t−x로 적분한다. 적분변수가 t이기 때문에 −x는 상수취급되어 (t−x)로 적분해도 괜찮다.)
=−(a−x)f′(a)−{[21(t−x)2f′′(t)]ax−∫ax21(t−x)2f(3)(t)}
=(x−a)f′(a)−21(a−x)2f′′(a)+∫ax21(t−x)2f(3)(t)dt
=(x−a)f′(a)+21(x−a)2f′′(a)+{[31⋅21(t−x)3f(3)(t)]ax−∫ax31⋅21(t−x)3f(4)(t)dt}
=(x−a)f′(a)+21(x−a)2f′′(a)+2⋅31(x−a)3f(3)(a)+⋯
f(x)−f(a)=(x−a)f′(a)+21(x−a)2f′′(a)+2⋅31(x−a)3f(3)(a)+⋯
f(x)=f(a)+(x−a)f′(a)+21(x−a)2f′′(a)+2⋅31(x−a)3f(3)(a)+⋯
=k=0∑∞k!f(k)(a)(x−a)k
테일러 급수의 의미
k=0∑∞k!f(k)(a)(x−a)k
테일러 급수의 일반화
이렇게 테일러 급수를 증명까지는 해보았는데, 그래서 어떤 의미를 가진다는 것인지는 식만봐서는 도통알기가 힘들다.
우선 증명과정에서 알 수 있듯이, 테일러 근사를 하려면 함수가 x=a에서 infinitely differentiable 해야한다. 예를 들면 sinx의 경우 sinx→cosx→−sinx→−cosx→sinx→⋯로 무한히 미분된다.
그리고 무한히 미분하는 과정에서 x=a에서의 n계 도함수 값들을 합하면서 함수값을 구한다. 즉, 테일러 급수는 x=a 근처에서 함수를 근사하는 것이다.
이때, 차수가 높아질수록 더 정확하게(넓게) 함수를 근사한다.
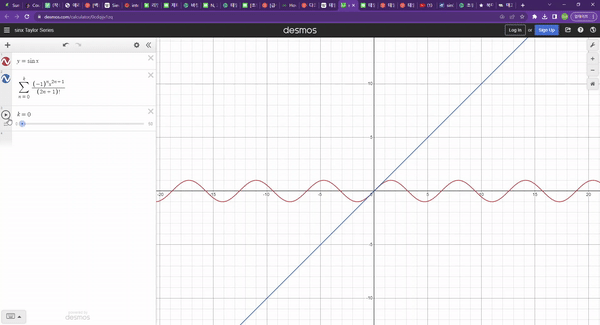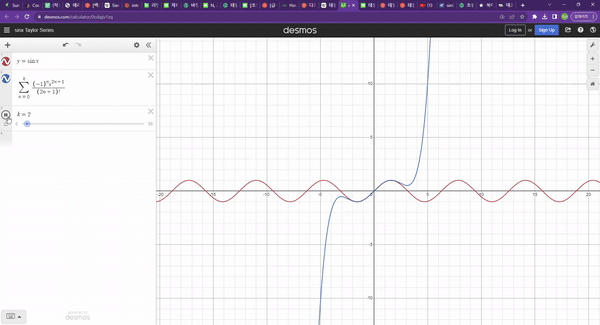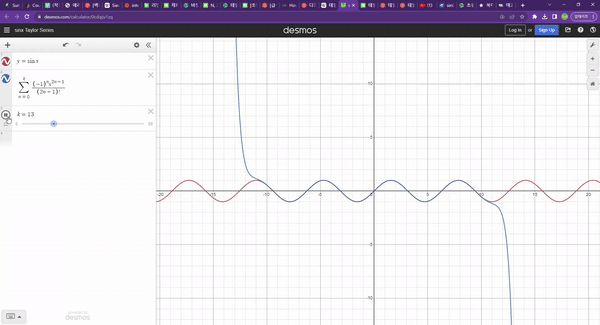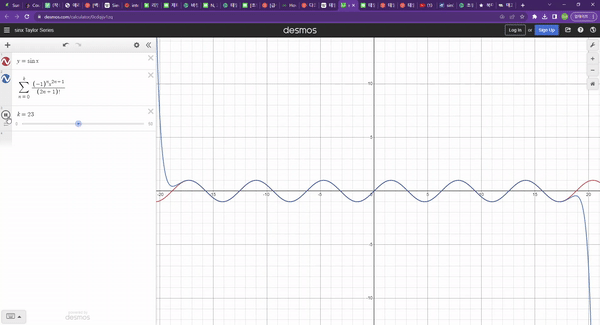 생각해보자, 함수를 한 번 미분하면 함수의 변화량(기울기)을 구할 수 있다. 그리고 이걸 한 번 더 미분하여 이계도함수를 구하면 함수의 변화량의 변화량이된다. 일계도함수는 함수의 두 점사이들의 관계가 될 것이고, 이계도함수는 두 점사이 관계들의 관계이다. 이러한 메커니즘으로 차수가 높아질수록 정확도도 높아진다.
생각해보자, 함수를 한 번 미분하면 함수의 변화량(기울기)을 구할 수 있다. 그리고 이걸 한 번 더 미분하여 이계도함수를 구하면 함수의 변화량의 변화량이된다. 일계도함수는 함수의 두 점사이들의 관계가 될 것이고, 이계도함수는 두 점사이 관계들의 관계이다. 이러한 메커니즘으로 차수가 높아질수록 정확도도 높아진다.
그러나, 우리가 구하고자 하는 식에 따라 차수를 높일 필요가 없는 경우도 있다.
예를 들어 x→0limxsinx=1의 식은 x=0 근처이므로 테일러 전개에 의해 아래와 같이 쓸 수 있다.
x→0limxsinx
=x→0limxx−3!x3+5!x5−⋯
=x→0lim(1−3!x2+5!x4−⋯)
=1−3!0+5!0−⋯
=1
고등수준에서의 증명
매클로린 급수
k=0∑∞k!f(k)(0)xk
a=0인 경우를 매클로린 급수라고 한다.
테일러 급수와 별개인 것이 아니라, 테일러 급수중에서도 a가 0인 경우 즉, 매클로린 급수는 테일러급수의 부분집합이다. 이렇게 따로 정의된 이유는 그만큼 많이 쓰이기 때문일것이다. 실제로 위에서 예시로 든 sinx도 매클로린 급수로 표현된것이다.
테일러 급수가 성립하려면 사실 조금 더 까다로운 조건이 필요하나 더 이상 깊어지면 글이 다소 난해해지는 감이 있으므로 이 글에서는 이 정도 수준으로 하고 넘어간다.
차수가 높아질수록 더 먼 거리의 값들을 비교하는 게 아니라 x=a라는 한 점 근처만을 계속해서 더 정확하게 값을 만들어준다고 생각한다. 그래서 솔직히 이해는 잘 안된다.
나름 이해한다고 노력해본건데 솔직히 제대로 이해한게 맞는지도 모르겠고 겉핥기만 한 것 같다... 그래도 일단 원래 목표인 에라토스테네스의 체를 증명하기에는 충분히 다룬 것 같다. 다음기회에 제대로 공부해봐야할 것 같다.
질문 및 지적 환영합니다.
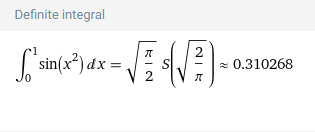
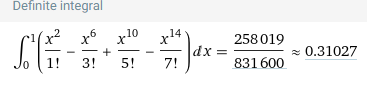
 생각해보자, 함수를 한 번 미분하면 함수의 변화량(기울기)을 구할 수 있다. 그리고 이걸 한 번 더 미분하여 이계도함수를 구하면 함수의 변화량의 변화량이된다. 일계도함수는 함수의 두 점사이들의 관계가 될 것이고, 이계도함수는 두 점사이 관계들의 관계이다. 이러한 메커니즘으로 차수가 높아질수록 정확도도 높아진다.
생각해보자, 함수를 한 번 미분하면 함수의 변화량(기울기)을 구할 수 있다. 그리고 이걸 한 번 더 미분하여 이계도함수를 구하면 함수의 변화량의 변화량이된다. 일계도함수는 함수의 두 점사이들의 관계가 될 것이고, 이계도함수는 두 점사이 관계들의 관계이다. 이러한 메커니즘으로 차수가 높아질수록 정확도도 높아진다.