[LeetCode] 204. Count Primes, 그리고 에라토스테네스의 체 시간복잡도 증명

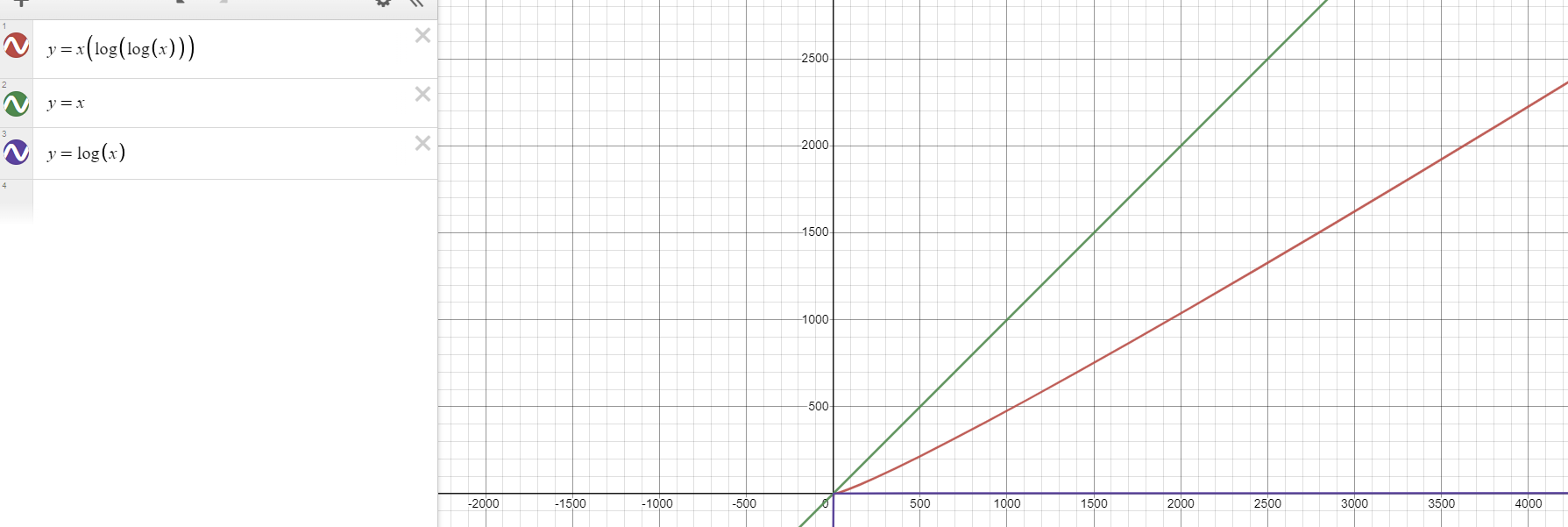
Intuition

문제를 보자마자 에라토스테네스의 체가 떠올랐다.
숫자 하나의 소수 여부를 판별하은 제곱근까지 나누어서 나누어 떨어지지 않는다면 소수라고 판단할 수 있다. 그러나 여러개의 소수를 대량으로 판별하는 데에는 에라토스테네스의 체가 훨씬 효과적이다. 문제를 풀때, strictly less than임에 유의하여 =를 붙일지 말지 판단하자.

Aproach && Solution

에라토스테네스의 체는 배수를 지우는 방식으로 작동한다. 각 수들의 배수를 지우고나면 결국엔 소수만 남게된다. 코드에서는 지우는 행위를 0을 할당시켜주는 방식으로 대체했다. 정리하면,
1. 숫자가 담긴 배열 생성
2. 모든 숫자를 순차적으로 돌면서
$\quad$ 2-1. 지워진 숫자(소수)라면 건너뛰고
$\quad$ 2-2. 그렇지 않다면, 해당 숫자를 제외한 해당 숫자의 배수를 지운다.
3. 0이 아닌 것들을 카운트해 소수가 몇 개인지 판단한다.

예를 들면,

• 2 3 4 5 6 7 8 9 10 // 초기상태
  -> 2 3 4 5 6 7 8 9 10 // 2의 배수를 지운 상태 (4,6,8,10)
  -> 2 3 4 5 6 7 8 9 10 // 3의 배수를 지운 상태 (6,9) (6은 이미 이전에 지워짐)
  -> 2 3 4 5 6 7 8 9 10 // 4는 지워졌으니 통과.
  -> 2 3 4 5 6 7 8 9 10 // 5의 배수 지우기 (10) (전에 이미 지워짐)

int countPrimes(int n){
    if (n==0) return 0;
    int nums[n]; 
    for (int i=2;i<n;i++){ // index 2에는 2, index 3에는 3 ...
        nums[i]=i;
    }

    for (int i=2;i<n;i++){
        if (nums[i]!=0){
            for (int j=i*2;j<n;j+=i){ // 배수들을 지워준다.
                nums[j]=0;
            }
        }
    }

    int cnt=0;
    for (int i=2;i<n;i++){
        if (nums[i]!=0){
            cnt++;
        }
    }
    return cnt;
}

그런데 이 코드를 조금 더 최적화시킬 수 있다는 것을 알게됐다.

첫번째, 제곱근까지만 체크하기. 단일 소수를 판단할 때와 같은 원리라고 한다.
단일 소수를 판단하는 것과 무엇이 동일한것인지 솔직히 이해가 잘 가지 않는다. 단일 소수판단에서 약수인지 판단하기 위해 제곱근까지 체크하는 것과, 여러개의 숫자들 가운데서 소수인지를 판단하기 위해 제곱근까지만 체크한다는 것은 다른 것 아닌가?
이해가 가지 않아 더 찾아봤을 때 납득이 되는 다른 답변을 찾을 수 있었다. 후술할 두번째 과정까지 적용하고 나면 $j=i\times i$부터 시작하는데, $i\times i>n$이면 중첩된 반복문의 조건에 맞지 않기 때문이다. (의미없이 큰 반복문만 더 돌아간다.)

for (int i=2;i<sqrt(n);i++){ // i*i<=n
        if (nums[i]!=0){
            for (int j=i*2;j<n;j+=i){
                nums[j]=0;
            }
        }
    }

앞으로, 중첩 for문을 쓸 때 $i,\,j$등이 서로 매개된다면 범위 등에 더욱 신경쓰자.

두번째, 제곱부터 체크 시작하기. 제곱 전의 숫자는 이미 체크한 부분이기 때문이다. 예를 들어, i=5일때, 5x2는 i=2일때 이미 체크했을 것이고, 5x3은 i=3일때 이미 체크했을 것이다. 따라서 5x5일때 부터 배수들을 지워주면 된다.

for (int i=2;i<sqrt(n);i++){
        if (nums[i]!=0){
            for (int j=i*i;j<n;j+=i){ // 바뀐 부분
                nums[j]=0;
            }
        }
    }

Complexity

• Time Complexity : 후술.
• Space Complexity : 숫자를 저장하기 위한 공간이 필요하다. $O(n)$

교수님 풀이

최적화 시킨 풀이와 동일하다.
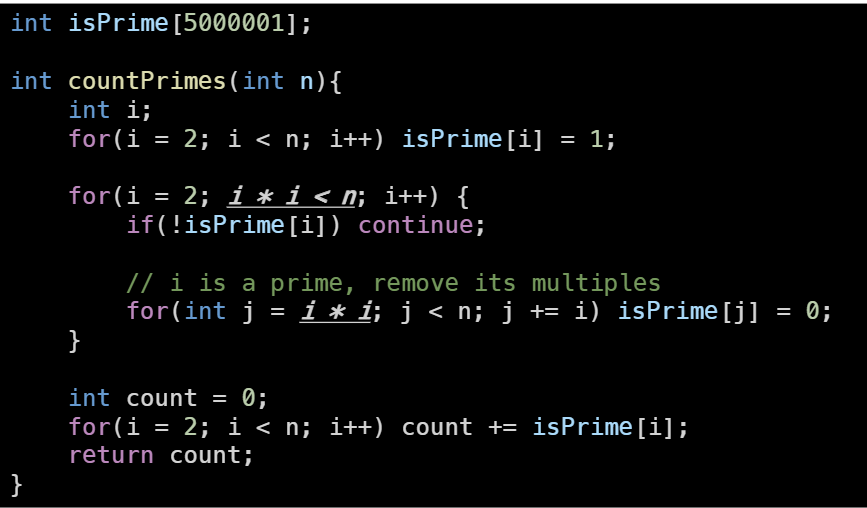위에서 이해하지 못한 부분도 설명해주셨지만 여전히 이해하지 못하겠다.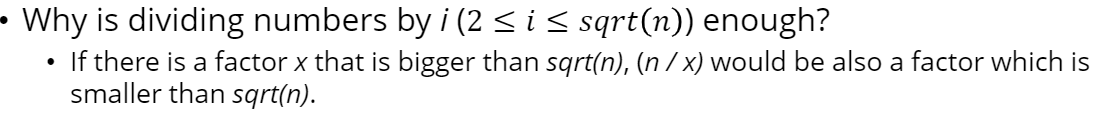그리고 math.h가 없을 때에는 i<sqrt(n)대신에 i*i<n을 쓸 수 있다.

Complexity

• Time Complexity : 먼저 rough한 time complexity는 아래와 같다.

일단 1, 3번째 for문은 $O(n)$임을 쉽게 알 수 있다.

중첩 for문 중 큰 for문은 $O(\sqrt n)$이다. 예를 들어 n=15면 i=2, 3 까지 밖에 안돈다.
작은 for문을 이해하는 게 당연하지만 지금까지 생각하지 못했던 부분이었는데, 우선 j부터 n이 될때까지 반복되므로 $n-j=n-i^2$이라 쓰고 이 반복이 i씩 커지며 반복되므로 $\frac{n-i^2}{i}$라 표현할 수 있다. 그리고 이때 최악의 경우는 i가 0에 수렴하여 최종 값이 가장 커지는 상황 즉, $O(n)$이다.

따라서 중첩 for문은 $O(n \sqrt n)$이고 최종적으로 $2n+n\sqrt n$에서 최고차항만 남게되니 $O(n \sqrt n)$이 된다.

Time Complexity

엄밀한 증명은 과정이 길어져서 따로 뺐다. 이하 증명에서 $log$는 자연로그를 의미한다.

이때는 중첩반복문을 바깥/안 별개로 구분해서 보면 복잡도를 구하기가 쉽지 않다.
바깥의 반복문을 보면 $\sqrt n$이고 안쪽의 반복문을 보니 ... 이렇게 하지 말라는 것

처음에는 2의 배수들을 지울 것이니 $n\over2$번 반복
물론 엄밀하게는 $\frac{n}{2}-1$이 맞지만 어차피 우리는 시간복잡도를 구할 것이니 이렇게 해도 괜찮다.

그 다음은 3의 배수를 지우니 $n\over3$번 반복, 그 다음은 4이므로 $O(1)$로 건너뛰고 5의 배수를 지우면서 $n\over5$번 반복 ... 즉, $\displaystyle{\frac{n}{2}+\frac{n}{3}+\frac{n}{5}+...=n(\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+...)=n\sum_{p}\frac{1}{p}}$으로 표현할 수 있는 것이다.

본격적인 증명에 앞서, 테일러 급수, 오일러 곱셈 공식 그리고 조화급수에 대해 알아야한다.

$\displaystyle\sum_{k=0}^{\infin}\frac{f^{(k)}(0)}{k!}x^k$
Maclaurin Series

$\displaystyle{\zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\cdots=\frac{1}{(1-\frac{1}{2^s})(1-\frac{1}{3^s})(1-\frac{1}{5^s})\cdots}=\prod_{p}\frac{1}{1-p^{-s}}}$
Euler Product Formula

$\displaystyle{\sum_{n=1}^{\infin}\frac{1}{n}=\theta(\log n)}$
Harmonic Series

이때, $0<p^{-1}<1$이고, 테일러 전개에 의해 $x=0$에서 $\displaystyle{log(1-x)=-x-\frac{x^2}{2}-\frac{x^3}{3}-\frac{x^4}{4}-\cdots}$라 알려져 있으므로, 아래와 같이 다시 쓸 수 있다.

등비급수의 합 공식에 의해,

이때, $\displaystyle{\sum_{p}\frac{1}{p(p-1)}<\sum_{n\in\mathbb{N}}\frac{1}{n(n-1)}}$에서 우변이 수렴하므로 비교판정법에 의해 좌변도 적당한 상수 $C$에 수렴함을 알 수 있다. 즉,

이라고 쓸 수 있고, $\displaystyle\sum_{p}\frac{1}{p}$가 조화급수에 의해 발산하는 속도가 $\log(\log(n))$에 근접함을 알 수 있다.

$\displaystyle{\therefore\,n\sum_{p}\frac{1}{p}=O(n\log(\log(n)))}$

지적 및 질문 환영합니다.