[LeetCode] 312. Burst Balloons

Ho__sing·2025년 1월 8일

C DP leetcode

문제해결 자체 재수강

목록 보기

49/49

Intuition

하나씩 풍선을 터뜨려가면서 그때그때 최선의 선택을 찾는 알고리즘은 불가능해보였다.
작은 케이스의 결과가 큰 케이스의 결과를 알아내는 데에 도움을 줄 수 있어보였다.

Approach

Def.) nums[i:j]에서 최대로 구할 수 있는 코인의 수를 coin[i][j]라 한다. (단, 0<=i,j<numsSize)
Goal) nums[0][numsSize-1]

풍선의 인덱스가 아래와 같을 때,
nums[i:j]의 범위에서 인덱스k의 풍선을 마지막으로 터뜨린다고 가정해보겠다. (단,i<=k<=j)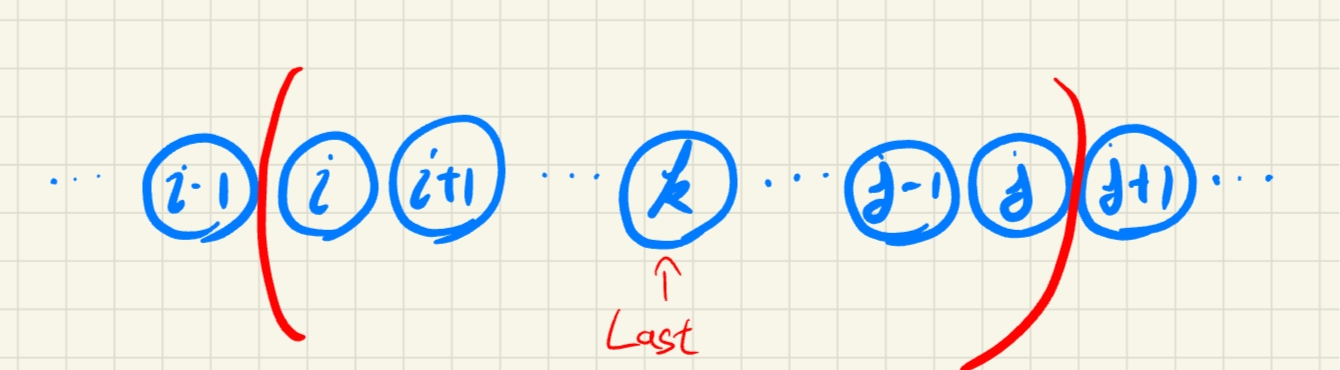그렇다면 그 이전까지의 과정이 어떻게 되었든 간에 [i:k-1]과 [k+1:j]까지의 풍선은 이미 터졌을 것이고 그 결과 coin[i][k-1]과 coin[k+1][j]를 획득했을 것이다. 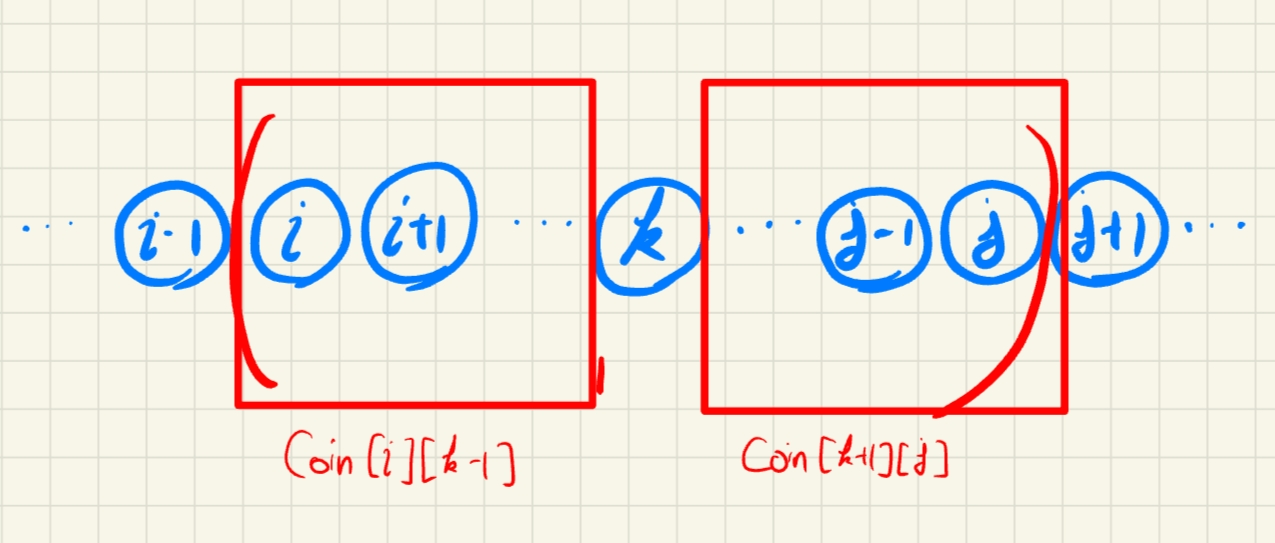이제 남은 풍선 k를 터뜨리게 되면 nums[i-1]*nums[k]*nums[j+1] 만큼의 코인을 획득하게 된다.범위에 있는 k중 어떤 것이 가장 높은 값을 갖는지 비교해보면 된다. 이에 따라 우리는 아래와 같이 점화식을 작성해볼 수 있다.

점화식) coin[i][j]=MAX(coin[i][k-1]+coin[k+1][j]+nums[i-1]*nums[k]*nums[j+1]) (단,i<=k<=j)

이번에도 마찬가지로 인덱스가 우리가 의도한 바와 벗어나지는 않는지 점검해본다. 아무래도 -와 +가 있다보니, i-1과 j+1일 때가 정의되지 않는 범위다. 정의상 coin[a][b]에서 a>b인 케이스는 성립하지 않기 때문에 0으로 처리한다.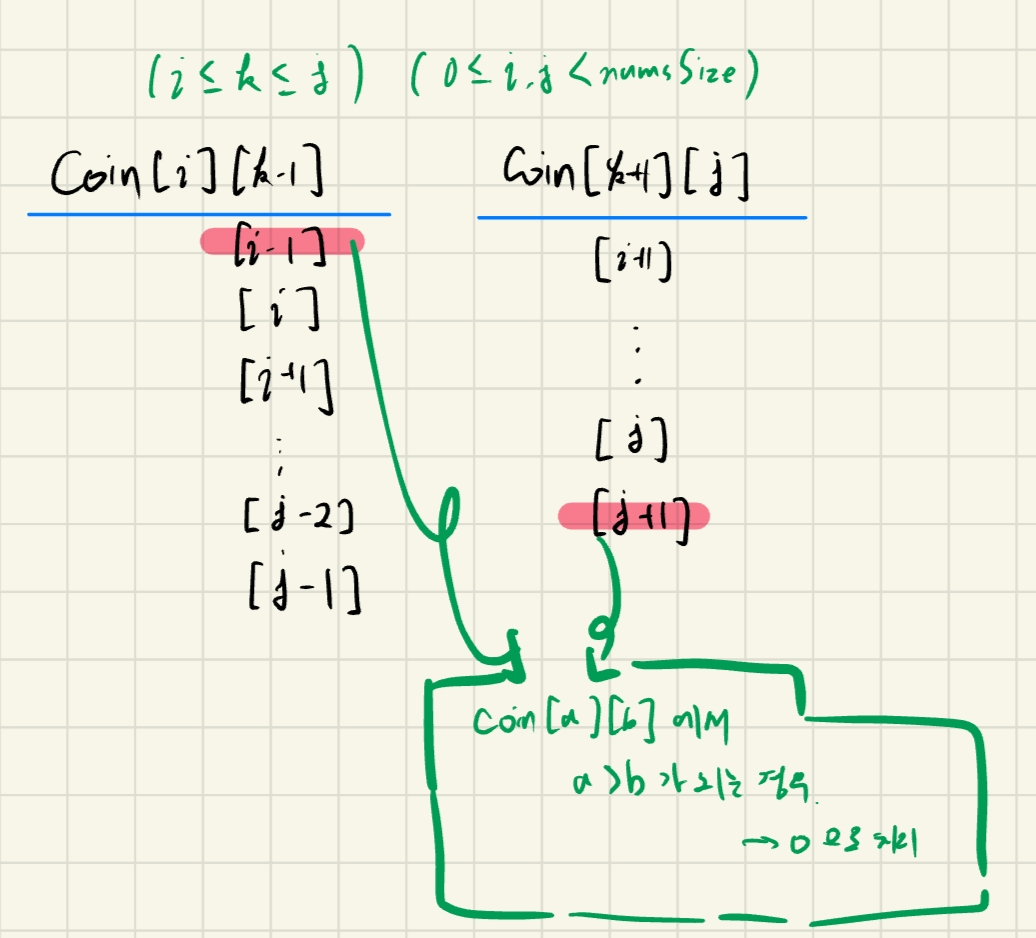이제 i와j를 어떤 순서로 순회할지 정해야한다. 쉽게 생각하기 위해, coin[1][2]를 구할 때, 어떤 인덱스들이 필요한지 찾아보겠다. k는 1또는 2가 가능하기 때문에 각각의 경우에 어떤 변수가 필요한지 아래와 같이 정리해볼 수 있다.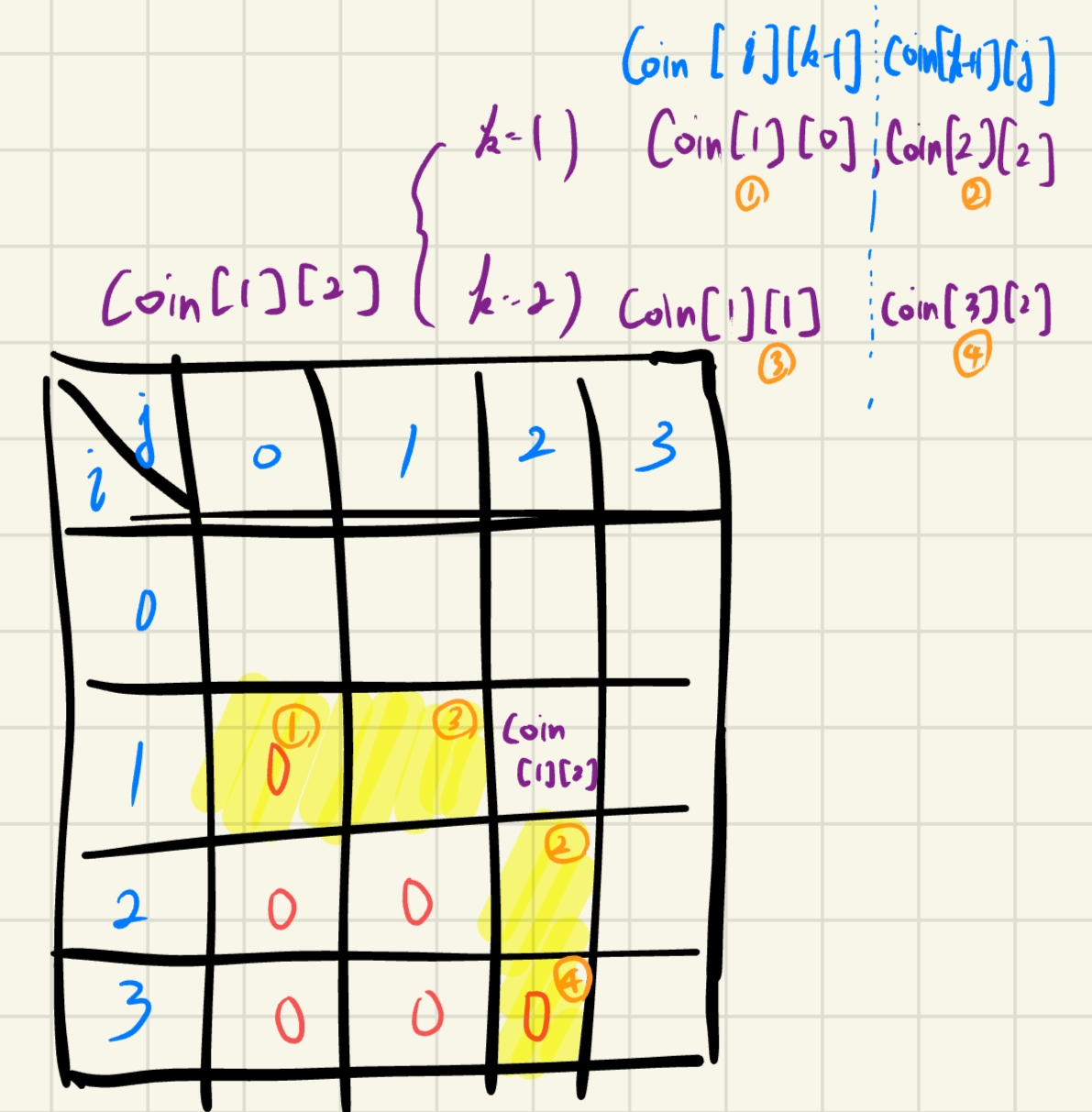
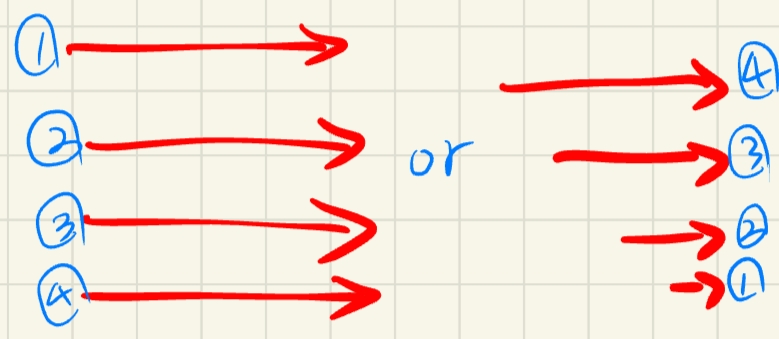
따라서 아래 그림과 같은 순서로 i,j를 순회할 때, 우리의 점화식대로 답을 구할 수 있다.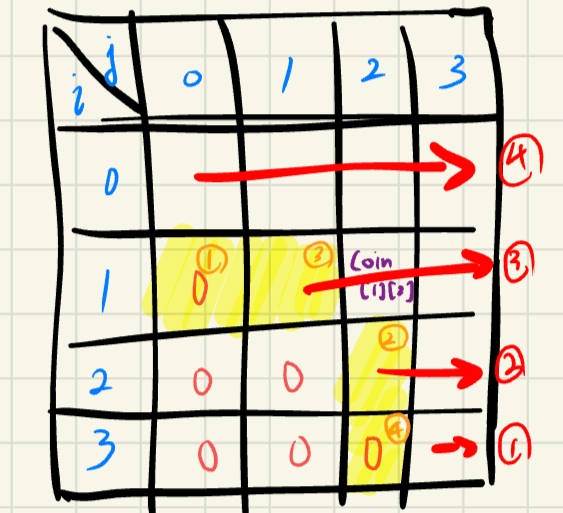

Solution

#define MAX(a,b) ((a)>(b)?(a):(b))
int coin[300][300];

int maxCoins(int* nums, int numsSize) {
    for (int i=numsSize-1;i>=0;i--){
        for (int j=0;j<numsSize;j++){
            int res=0;
            for (int k=i;k<=j;k++){
                int left_coin=i>k-1?0:coin[i][k-1];
                int right_coin=k+1>j?0:coin[k+1][j];
                int left_balloon=i-1<0?1:nums[i-1];
                int mid_balloon=nums[k];
                int right_balloon=j+1>=numsSize?1:nums[j+1];
                res=MAX(left_coin+right_coin+left_balloon*mid_balloon*right_balloon,res);
            }
            coin[i][j]=res;
        }
    }
    return coin[0][numsSize-1];
}