Intuition

작은 문자열부터 원래문자열까지 하나씩 늘려가며 문제를 해결할 수 있을 것이라 예측했다.

Approach

문제 재해석

Def.) arr[i][j]:=word1[:i]가 word2[:j]로 convert 되는데 필요한 최소 cost

위와 같이 부분 문제를 정의해줄 수 있다.
따라서, 최종목표는 아래와 같이 정의할 수 있다.

Goal) arr[strlen(word1)][strlen(word2)]

base case는 아래 두 경우가 되겠다.

Base case) arr[i][0]=i, arr[0][i]=i

길이 i의 문자열을 빈 문자열로 만들거나, 빈 문자열을 길이 i의 문자열로 만드는데에는 i만큼이 소요된다.

Cost 계산

Case1: word1[i]!=word2[j]

word1[i]와 word2[j]가 같은지 다른지에 따라 cost의 결정 알고리즘이 달라진다.
먼저 다른 경우를 살펴보겠다. 예를 들어, word1[:1]인 h를 word2[:1]인 r로 바꾸는 경우에 대해 생각해보겠다.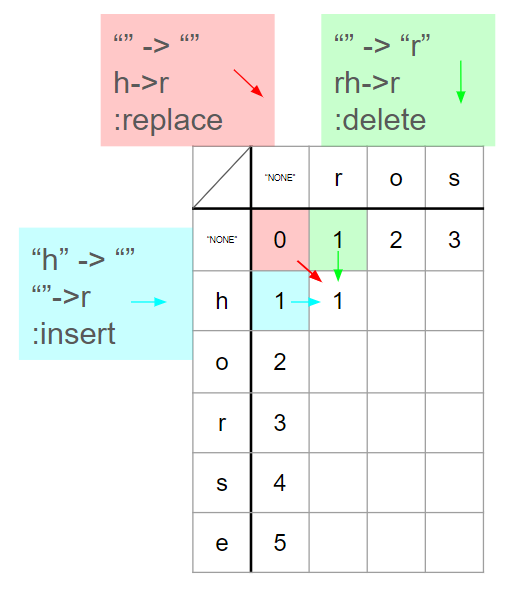

Delete

초록색 부분을 먼저 살펴보자. 기존에 아무것도 없는 문자열에서 'r'로 바꾸는 데에 이미 비용 1 이 필요했다. 그런데 여기서 word1에 'h'가 추가되는 상황이 발생한다.

arr[1][1]은 arr[0][1]의 값에 word1에 'h'를 추가하는 연산만 더해 계산하면 된다. 비록 arr[1][1]을 h->r로 표현할 수 있지만, 실제로는 arr[0][1]에서 이미 "" -> r 과정이 이루어졌다고 가정할 수 있다. 즉, 이 단계에서 word1은 이미 'r'로 변환된 상태이다.

이제 arr[1][1]에서 word1에 'h'라는 문자가 추가되었기 때문에 'rh -> r' 상태가 된다. 이 경우 'h'를 삭제해야 하는 비용이 추가적으로 발생하게 된다.

Insert

다음으로 파란색 부분을 보겠다. 기존 'h'를 "none"으로 바꾸는 과정에서 이미 비용 1이 필요했다. word1은 이미 비용1을 소모하여 빈 문자열로 바뀌어있다는 것이다. 이 상태에서 word2[:1]인 'r'로 convert 하기 위해서는 'r'을 추가해주는 비용 1이 추가적으로 필요하다.

Replace

기존이 빈 문자열끼리의 비교였기 때문에 arr[1][1]을 계산하는 과정에서 word1과 word2 모두 각각 'h'와 'r'을 추가적으로 갖게 된다. 즉, 'h->r'인 과정을 계산하는 것이다. 'h'를 'r'로 대체해주는 비용 1이 필요하게 된다.

다만 기존 arr[0][0]에서 소모된 비용이 없기 때문에 비용 1이 추가적으로 쓰이더라도 결과값이 1이된다.

이처럼 word1[i]와 word2[j]가 다를 때는 대각선, 위, 왼쪽의 값을 가져오는 방식에 따라 각각 replace, delete, insert 연산이 결정된다. 즉, 세 연산에 대한 모든 경우를 비교하여 기존 비용(cost)이 가장 작은 위치에서 +1을 해주면 된다.

arr[i][j]=min(arr[i-1][j-1],arr[i][j-1],arr[i-1][j])+1 if(word1[i]!=word2[j])

Case2: word1[i]==word2[j]

이제 word1[i] == word2[j]인 상황에 대해 알아보겠다.

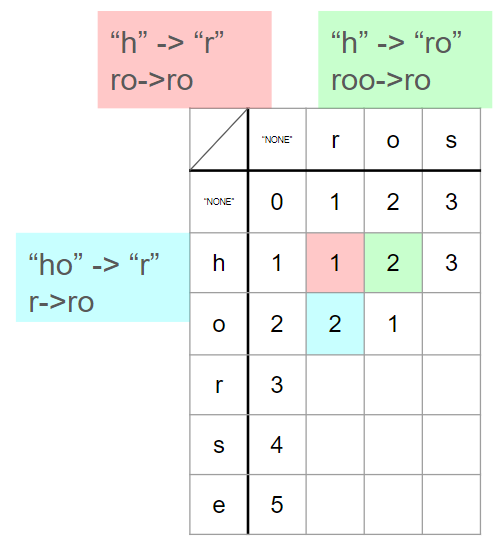
초록색과 파란색의 경우, 이전 과정에서 이미 'o'에 대한 비용이 발생했다. (각각 'o'를 insert, delete한 비용이다.) 그러나 빨간색의 경우 'o'에 대한 비용이 아직 발생하지 않았기 때문에, 'o'가 추가되었을 때 같은 문자라는 이점을 이용하여 이전 비용을 그대로 유지할 수 있다.

arr[i][j]=arr[i-1][j-1] if(word1[i]==word2[j])

Solution

#include <string.h>

int arr[501][501];

int MIN(int a, int b, int  c){
    int num[3]={a,b,c};
    int ret=a;

    for (int i=0;i<3;i++) if (ret>num[i]) ret=num[i];

    return ret;
}

int minDistance(char* word1, char* word2) {
    int m=strlen(word1);
    int n=strlen(word2);
    
    for (int i=0;i<m+1;i++) arr[i][0]=i;
    for (int i=0;i<n+1;i++) arr[0][i]=i;

    for (int i=1;i<m+1;i++){
        for (int j=1;j<n+1;j++){
            if (word1[i-1]==word2[j-1]) arr[i][j]=arr[i-1][j-1];
            else arr[i][j]=MIN(arr[i-1][j-1],arr[i-1][j],arr[i][j-1])+1;
        }
    }

    return arr[m][n];
}

Time Complexity

$O(N*M)$

그 외

이 문제는 다른 이름으로 Levenshtein distance라고도 불리며, 단어의 형태적 유사도를 측정하는 알고리즘이다.

만약에 문제가 어떤 연산이 어떤 순서로 쓰였는지 구하라하면 arr[n][m]에서 부터 어떻게 왔는지 그 과정을 거꾸로 타고 올라가면서 스택에 push하고 pop해주면 된다.

지적 및 질문 환영