Intuition

이 문제를 한 줄로 요약하면 (길이)*(최솟값)을 최대로 만드는 것이다.
길이를 확정시킨다음 최솟값을 결정할 수도 있고, 최솟값을 결정한 다음 길이를 최대화시킬 수도 있다. 나는 전자의 경우 $O(N)$, 후자의 경우 그보다는 효율적일 것이라고 판단해서 후자의 방식을 택했다.
물론 막상 코드를 짜고나니 후자도 $O(N)$이 소요됐다.

Approach

Rough한 흐름은 아래와 같다.

배열 전체에서의 최솟값은 1이므로, (길이)$*$(최솟값)이 최대가 되려면 길이는 배열전체가 되고 그 값이 6*1=6가 된다.

배열 전체에서 1을 제외한 그 다음 최솟값은 3이다. 이번에 (길이)$*$(최솟값)이 최대가 되려면, 1이 있는 Index가 제외되도록 길이를 설정해주어야하고, 그 값은 5*3=15가 된다.

배열 전체에서 1과3을 제외한 그 다음 최솟값은 4이다. 이번에 (길이)$*$(최솟값)이 최대가 되려면, 이전 Index에서 3이 있는 Index가 제외되도록 길이를 설정해주어야하고, 그 값은 3*4=12가 된다.

위와 같은 과정을 k$^{th}$ Index가 최솟값이 될때까지 반복해준다.

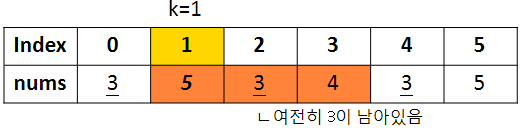
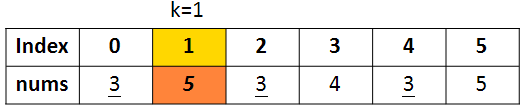
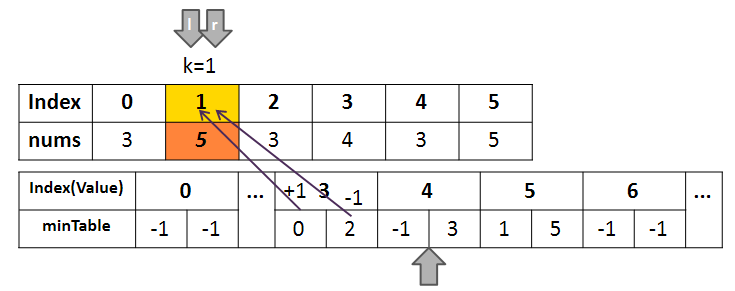
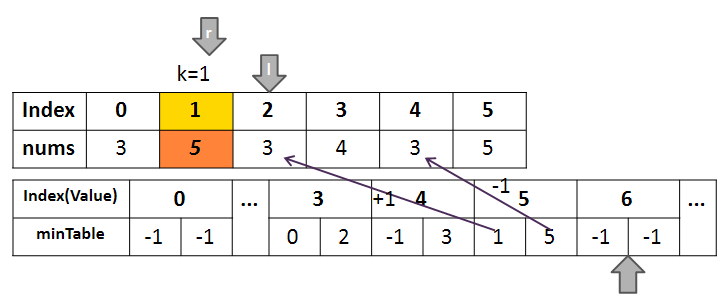
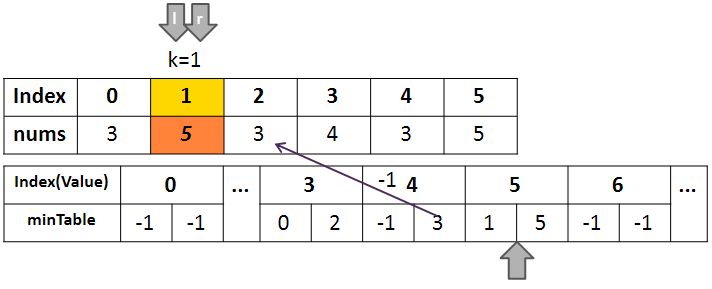
위와 같은 implementation을 위해서는 최솟값이 무엇이고 어디있는지 미리 확인해놓으면 효율적이다. 그런데 이때 중요한 것은 k를 기준으로 양옆에서 가장 가까운 쪽의 index를 체크해야한다는 것이다. 이유인 즉슨, 아래와 같이 3이라는 최솟값이 여러개 있다고 가정해보자.이 상황에서 최솟값 3을 제외하려면 k왼쪽의 경우 Index 0의 다음인 1로 옮겨주면 되지만, 오른쪽의 경우 Index 4와는 관계없이 k쪽에 가까운 Index 2의 이전인 1로 옮겨주어야 하기 때문이다.
이를 위해, k이전의 경우에는 계속해서 값을 업데이트해주고, 이후의 경우에는 최초 1회만 값을 업데이트 해준다.

    int minTable[20001][2];
    for (int i=0;i<20001;i++){
        minTable[i][0]=minTable[i][1]=-1;
    }

    for (int i=0;i<numsSize;i++){
        if (i<=k) minTable[nums[i]][0]=i;
        else if (minTable[nums[i]][1]==-1) minTable[nums[i]][1]=i;
    }

이제 minTable 배열을 순회하며 nums배열에서 그때그때의 최솟값을 제외해주며 최댓값을 결정시켜주기만 하면 된다.
#1)#2)

    int l,r,max;
    l=0,r=numsSize-1,max=0;
    for (int i=0;i<20001;i++){
        ...
        if (minTable[i][0]!=-1||minTable[i][1]!=-1){
            if (max<(r-l+1)*i) max=(r-l+1)*i;
            if (minTable[i][0]!=-1&&...) l=minTable[i][0]+1;
            if (minTable[i][1]!=-1&&...) r=minTable[i][1]-1;
        }
    }

그런데 이때 중요한 것은, l의 Index값이 더 작아진다거나 r의 값이 더 커지면 최솟값이 바뀌기 때문에 l과 r은 한 방향으로만 나아가야한다.
#3)

    int l,r,max;
    l=0,r=numsSize-1,max=0;
    for (int i=0;i<20001;i++){
        ...
        if (minTable[i][0]!=-1||minTable[i][1]!=-1){
            if (max<(r-l+1)*i) max=(r-l+1)*i;
            if (minTable[i][0]!=-1&&minTable[i][0]+1>l) l=minTable[i][0]+1; // l과 r이 한방향으로만 나아가도록
            if (minTable[i][1]!=-1&&minTable[i][1]-1<r) r=minTable[i][1]-1; // l과 r이 한방향으로만 나아가도록
        }
    }

k$^{th}$ Index가 최솟값이 되어 l또는 r이 k를 넘어가게 되면 반복을 완료한다.
#4)

    int l,r,max;
    l=0,r=numsSize-1,max=0;
    for (int i=0;i<20001;i++){
        if (l>k||k>r) break; // 반복 중지
        if (minTable[i][0]!=-1||minTable[i][1]!=-1){
            if (max<(r-l+1)*i) max=(r-l+1)*i;
            if (minTable[i][0]!=-1&&minTable[i][0]+1>l) l=minTable[i][0]+1;
            if (minTable[i][1]!=-1&&minTable[i][1]-1<r) r=minTable[i][1]-1;
        }
    }

Solution

int maximumScore(int* nums, int numsSize, int k){
    int minTable[20001][2];
    for (int i=0;i<20001;i++){
        minTable[i][0]=minTable[i][1]=-1;
    }

    for (int i=0;i<numsSize;i++){
        if (i<=k) minTable[nums[i]][0]=i;
        else if (minTable[nums[i]][1]==-1) minTable[nums[i]][1]=i;
    }

    int l,r,max;
    l=0,r=numsSize-1,max=0;
    for (int i=0;i<20001;i++){
        if (l>k||k>r) break;
        if (minTable[i][0]!=-1||minTable[i][1]!=-1){
            if (max<(r-l+1)*i) max=(r-l+1)*i;
            if (minTable[i][0]!=-1&&minTable[i][0]+1>l) l=minTable[i][0]+1;
            if (minTable[i][1]!=-1&&minTable[i][1]-1<r) r=minTable[i][1]-1;
        }
    }

    return max;
}

Complexity

Time Complexity && Space Complexity

$O(N)$

교수님 풀이

교수님은 내가 앞서 Intuition에서 언급했던 두 가지 방식중 전자를 택하셨다. 그리고 이게 실제로 훨씬 코드가 간단하기도 하다.

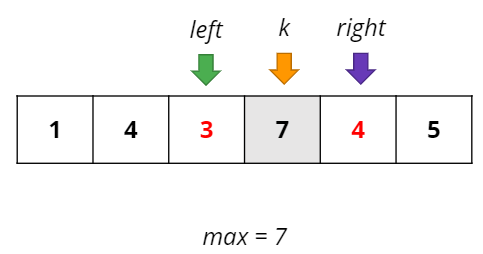
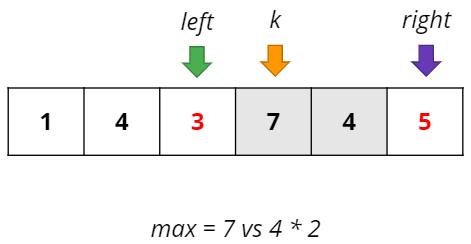
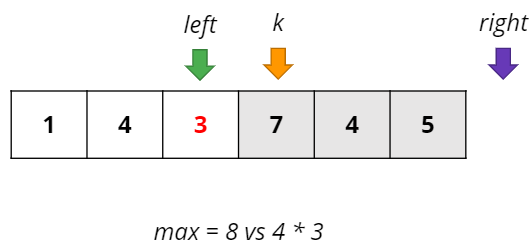
길이를 1씩 늘리는 풀이이므로 k를 기준으로 양 옆 숫자중 더 큰 쪽을 택하는 것이 (길이)*(최솟값)에서 최솟값을 더 크게 만들어 줄 수 있다.

    int l,r,max,min; // l, r 은 index
    l=r=k;
    max=min=nums[k];

    int leftNum, rightNum; // leftNum, rightNum은 value
    while (...){
        leftNum=nums[l-1];
        rightNum=nums[r+1];

        if (leftNum>rightNum){
            if (min>leftNum) min=leftNum;
            l--;
        }
        else {
            if (min>rightNum) min=rightNum;
            r++;
        }

        if (max<(r-l+1)*min) max=(r-l+1)*min;
    }

이때, left나 right가 이동하는 과정에서 인덱스를 벗어날 수도 있으므로 따로 처리가 필요하다. left, right 모두 인덱스를 벗어나면 모든 길이에 대해 탐색을 완료한 것이므로 반복문을 종료한다.

    int l,r,max,min;
    l=r=k;
    max=min=nums[k];

    int leftNum=1, rightNum=1; // 둘 다 0이되면 
    while (leftNum+rightNum>0){ // 반복문을 종료한다
    
        leftNum=l>0?nums[l-1]:0; // index를 벗어나는
        rightNum=r<numsSize-1?nums[r+1]:0;// case에 대한 처리

        if (leftNum>rightNum){
            if (min>leftNum) min=leftNum;
            l--;
        }
        else {
            if (min>rightNum) min=rightNum;
            r++;
        }

        if (max<(r-l+1)*min) max=(r-l+1)*min;
    }

Solution

int maximumScore(int* nums, int numsSize, int k){
    int l,r,max,min;
    l=r=k;
    max=min=nums[k];

    int leftNum=1, rightNum=1;
    while (leftNum+rightNum>0){
        leftNum=l>0?nums[l-1]:0;
        rightNum=r<numsSize-1?nums[r+1]:0;

        if (leftNum>rightNum){
            if (min>leftNum) min=leftNum;
            l--;
        }
        else {
            if (min>rightNum) min=rightNum;
            r++;
        }

        if (max<(r-l+1)*min) max=(r-l+1)*min;
    }

    return max;
}

Complexity

Time Complexity && Space Complexity

$O(N)$

지적 및 질문 환영