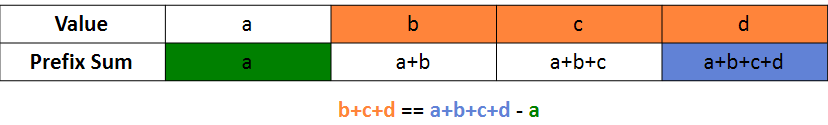Intuition

left, mid, right의 범위를 지정해주는 것이 우선적으로 필요하다.
한번에 지정하기는 힘들기 때문에, left를 먼저 지정하고 나머지 mid와 right를 지정하는 느낌으로 생각했다.

Approach

본격적으로 시작하기에 앞서, 그때그때 각 범위에 따른 합을 구해줘야하는 경우가 있으므로, 이 합을 $O(1)$에 구하기 위해 누적합을 사용하겠다.
누적합은 아래 그림과 같이 각 원소들의 합을 누적시킨 새로운 배열을 하나 만들어주면 된다.
여기서 index 1에서부터 index 3까지의 합을 구하고 싶다면 prefix sum의 index 3에서 prefix sum의 index 0의 값을 빼주면 된다.
8+4+2 == 15 - 1
증명은 아래와 같이 간단하게 할 수 있다.

즉, 일반화하면 배열의 index a부터 b까지의 합은 누적합 배열의 index b 에서 a-1을 뺀 것과 같다 라고 할 수 있다.

    int *arr = (int*)malloc(sizeof(int)*numsSize);
    int sum=0;
    for (int i=0;i<numsSize;i++){
        sum+=nums[i];
        arr[i]=sum;
    }

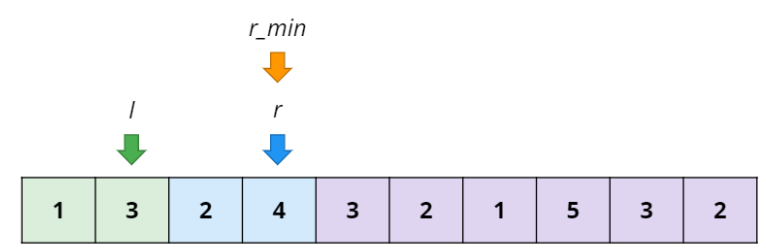
left와 mid의 끝부분을 각각 l, r 로 표현하면 아래와 같다.
위 상황에서 left의 합은 4, mid의 합은 2로 조건에 만족하지 않는다.

r의 index를 1늘리면 조건에 만족하는 상황이 된다. 그리고 이 시점이 조건을 만족하는 r의 최솟값이므로 r_min이라고 칭한다.

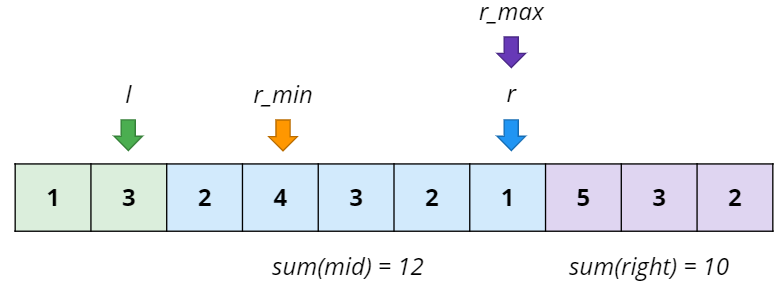
아래 상황은 조건을 만족하는 경우 중 r이 최대값인 경우이다. 이때의 r을 r_max라 칭한다.

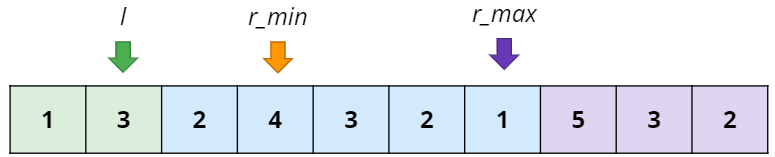
그리고 이 배열의 원소들은 0이 아닌 양수이므로 r_min과 r_max사이에 위치한 원소들은 무조건 조건을 만족하는 경우들이다. 따라서 l의 index가 1일때 조건을 만족하는 경우의 수는 r_max의 index에서 r_min의 index를 뺀 값이 된다.그리고 l의 index를 2로 조정하고 앞선 과정들을 반복해주면 l의 index에 따른 경우의 수들을 count할 수 있다.

    int rMin=1, rMax=1;
    int ret=0;
    for (int l=0;l<numsSize-2;l++){
        if (rMin<=l) rMin=l+1;
        while (rMin<numsSize-1&&arr[l]>arr[rMin]-arr[l]) rMin++;
        if (rMax<rMin) rMax=rMin;
        while (rMax<numsSize-1&&arr[rMax]-arr[l]<=arr[numsSize-1]-arr[rMax]) rMax++;
        ret=(ret+rMax-rMin)%1000000007;
    }

Solution

int waysToSplit(int* nums, int numsSize){
    int *arr = (int*)malloc(sizeof(int)*numsSize);
    int sum=0;
    for (int i=0;i<numsSize;i++){
        sum+=nums[i];
        arr[i]=sum;
    }

    int rMin=1, rMax=1;
    int ret=0;
    for (int l=0;l<numsSize-2;l++){
        if (rMin<=l) rMin=l+1;
        while (rMin<numsSize-1&&arr[l]>arr[rMin]-arr[l]) rMin++;
        if (rMax<rMin) rMax=rMin;
        while (rMax<numsSize-1&&arr[rMax]-arr[l]<=arr[numsSize-1]-arr[rMax]) rMax++;
        ret=(ret+rMax-rMin)%1000000007;
    }
    free(arr);
    return ret;
}

Complexity

Time Complexity

l의 index가 늘어날때 r_min과 r_max의 index가 줄어들지 않는것이 핵심이다. left의 합이 늘어나면 mid의 합은 줄어들기 때문이다. 이러한 이유로 l이 모든 iteration을 끝내는 동안에도 r_min과 r_max도 각각 배열을 한번씩만 돌게된다. 따라서 $O(3N)=O(N)$

Space Complexity

$O(N)$

지적 및 질문 환영