Intuition

문제를 좀 더 간단하게 생각해보면, k-1번 나눠서 그때마다 사과가 최소 1개 이상 있도록 만들어주는 문제이다. 그러기 위해 매번 선을 나눌때마다, 위아래 또는 양옆에 모두 사과가 있는 유효한 선인지를 검증하며 모든 경우의 수를 카운트하는 방식을 택했다.

피자를 자르는 과정에서 이후의 연산이 이전 값에 영향을 미치지 않는 것에서 재귀에 대한 가능성을 볼 수 있다고 한다.

처음에는 단순히 나눌 수 있는 가로 세로 선의 조합의 경우의 수를 구하는 것이라고 생각했는데, 이 문제의 경우는 한 번 선을 가를 때마다 가로선은 아래, 세로선은 오른쪽 것만 자를 수 있기 때문에 이러한 방법은 적절하지 못하다.

Approach1

단계적으로 구체화하며 pseudo code를 작성해보겠다.

void func(시작 가로선, 시작 세로선, 끝 가로선, 끝 세로선, k){
  if (전체 타일에 사과 존재 and k==0) 결과값++
  else{
	if (가로선 기준으로 위,아래 사과 존재) func(시작 가로선+1, 시작 세로선, 끝 가로선, 끝 세로선, k-1)
	if (세로선 기준으로 양옆 사과 존재) func(시작 가로선, 시작 세로선+1, 끝 가로선, 끝 세로선, k-1)
  }
}

재귀 함수로서의 기본적인 틀을 작성해봤다. 그러나 이렇게만 작성하게 되면, 모든 경우의 수를 확인할 수 없다. 간단하게 생각해서 무조건 가로선 먼저 나누게 되는 경우만 생각하게 된다. 이를 해결하기 위해 아래와 같이 작성해볼 수 있다.

void func(시작 가로선, 시작 세로선, 끝 가로선, 끝 세로선, k){
  if (전체 타일에 사과 존재 and k==0) 결과값++
  else{
  	for (i=시작 가로선 to 끝 가로선-1){
    	if (i+1 기준으로 위,아래 사과 존재) func(i+1, 시작 세로선, 끝 가로선, 끝 세로선, k-1)
    }
    for (i=시작 세로선 to 끝 세로선-1){
    	if (i+1 기준으로 양옆 사과 존재) func(시작 가로선, i+1, 끝 가로선, 끝 세로선, k-1)
    }
  }
}

이를 코드로 구체화시켜 작성해보면 아래와 같다.

int rowMax, columnMax;
int res;

/* 주어진 범위 내의 타일에 사과가 존재하는지 확인하는 함수 */
int check (char** pizza, int row, int column, int rowMax, int columnMax) {
    for (int i=row;i<rowMax;i++){
        for (int j=column;j<columnMax;j++){
            if (pizza[i][j]=='A') return 1;
        }
    }
    return 0;
}

void func (char** pizza, int row, int column, int k, int rowFin, int columnFin){
    if (check(pizza,row,column,rowFin,columnFin)&&k==0) res++;
    else{
        for (int i=row;i<rowFin-1;i++){
            if (check(pizza,row,column,i+1,columnFin)&&check(pizza,i+1,column,rowFin,columnFin)) func(pizza,i+1,column,k-1,rowFin,columnFin);
        }
        for (int i=column;i<columnFin-1;i++){
            if (check(pizza,row,column,rowFin,i+1)&&check(pizza,row,i+1,rowFin,columnFin)) func(pizza,row,i+1,k-1,rowFin,columnFin);
        }
    }

}

int ways(char** pizza, int pizzaSize, int k) {
    res=0;
    rowMax=pizzaSize;
    columnMax=0;
    for (int i=0;pizza[0][i]!=0;i++){
        columnMax++;
    }
    func(pizza,0,0,k-1,rowMax,columnMax);   

    return res;
}

Complexity

그러나 이 방식은 큰 시간복잡도로 몇몇 테스트케이스를 통과할 수 없다.

Time Complexity

재귀의 branch에 대해서만 살펴보겠다. row+column=N 이라고 하자.
func함수를 한 번 호출하게 되면 최악의 경우 N개의 func함수가 재호출된다.

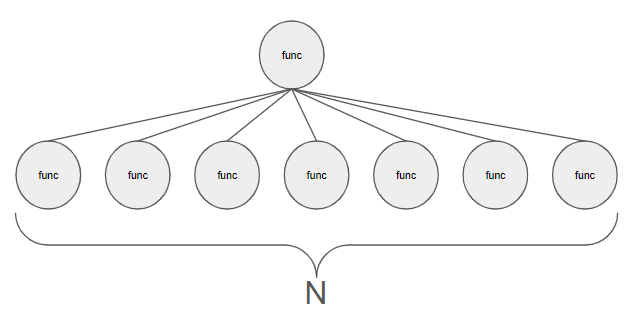
또, 그 N개의 func함수에서 각각 N개식 func함수가 재호출된다.

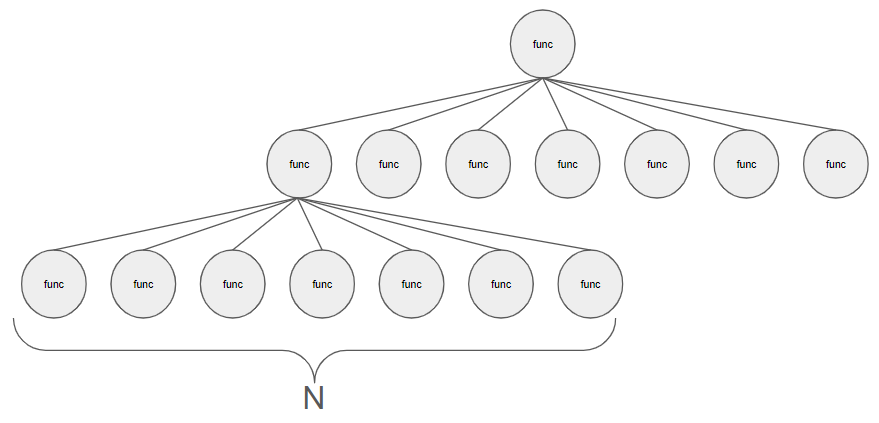
첫 레이어에서는 1개, 그 다음에는 N개, 그 다음 레이어에서는 N개씩 N개가 호출된다. 이때 레이어는 k로 상수화시킬 수 있다.

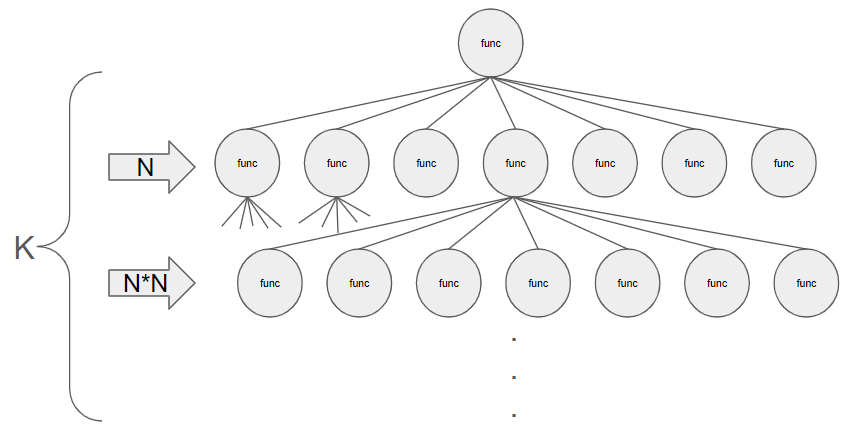
$1+N+N^2+\cdots+N^k$으로 표현할 수 있다. k의 최댓값은 10이고, N의 최댓값은 100이다.
따라서, $1+10^2+10^4+\cdots+10^{20}$으로 매우 큰 수임을 알 수 있다.

Space Complexity

$O(N)$

Approach2

시간복잡도를 개선시키기 위해서 약간의 공간복잡도를 희생해야할 필요가 있다.

함수를 호출하다보면, 이미 일전에 확인했던 경우의 수를 중복해서 확인하는 케이스가 발생한다.

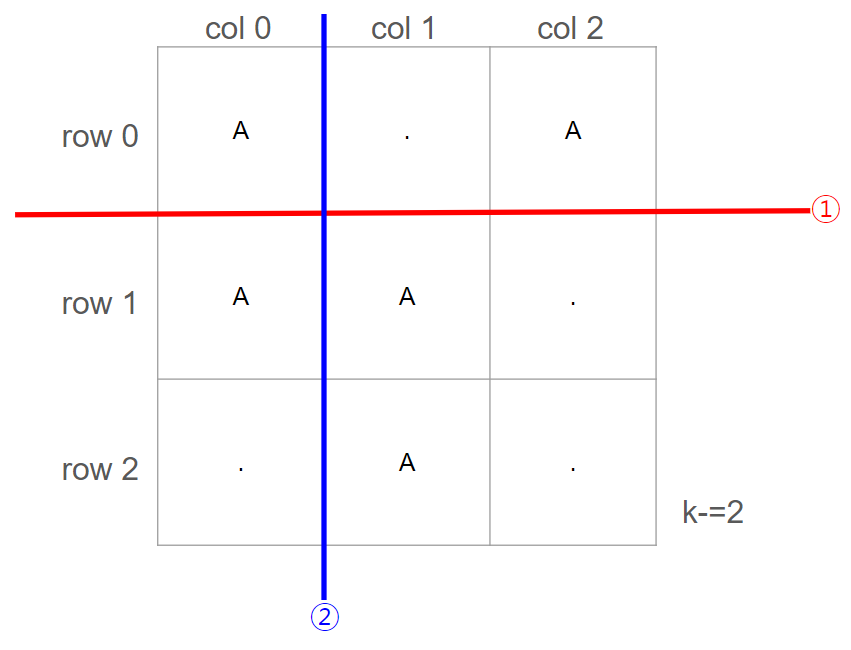
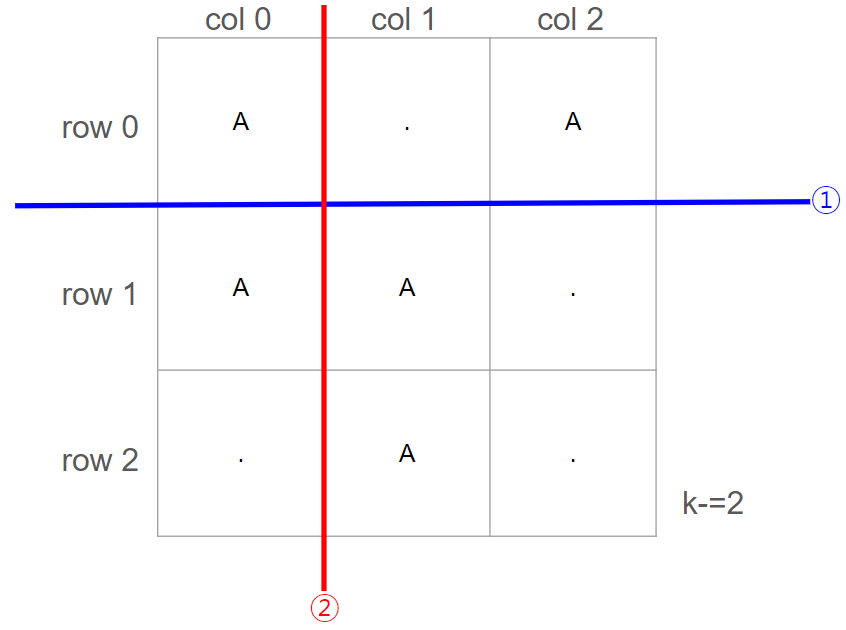Approach1에서 두 케이스는 각각 서로 다른 케이스로 취급된다. 그러나, 이 두 케이스 모두 (row1,co1)부터 (row2,col2)까지의 타일에 대해 k-=2된 조건에서 다음 케이스로 진행된다. 즉, 다음에 진행되는 케이스가 동일하다는 뜻이다.

dp를 적용하여 코드를 재작성해볼 수 있다.

Solution

int rowMax, columnMax;
int dp[50][50][10];

int check (char** pizza, int row, int column, int rowMax, int columnMax) {
    for (int i=row;i<rowMax;i++){
        for (int j=column;j<columnMax;j++){
            if (pizza[i][j]=='A') return 1;
        }
    }
    return 0;
}

int func (char** pizza, int row, int column, int k, int rowFin, int columnFin){
    int ret=0;
    if (dp[row][column][k]!=-1) return dp[row][column][k];
    if (check(pizza,row,column,rowFin,columnFin)&&k==0) return 1;
    else{
        for (int i=row;i<rowFin-1;i++){
            if (check(pizza,row,column,i+1,columnFin)&&check(pizza,i+1,column,rowFin,columnFin)) {
                ret+=func(pizza,i+1,column,k-1,rowFin,columnFin);
                ret%=1000000007;
            }
        }
        for (int i=column;i<columnFin-1;i++){
            if (check(pizza,row,column,rowFin,i+1)&&check(pizza,row,i+1,rowFin,columnFin)){
                ret+=func(pizza,row,i+1,k-1,rowFin,columnFin);
                ret%=1000000007;
            } 
        }
    }

    dp[row][column][k]=ret;
    return ret;

}

int ways(char** pizza, int pizzaSize, int k) {

    for (int i=0;i<50;i++){
        for (int j=0;j<50;j++){
            for (int k=0;k<10;k++) dp[i][j][k]=-1;
        }
    }

    rowMax=pizzaSize;
    columnMax=0;
    for (int i=0;pizza[0][i]!=0;i++){
        columnMax++;
    }

    return func(pizza,0,0,k-1,rowMax,columnMax);   
}

지적 및 질문 환영