[AI_basic] Overfitting, Underfitting, Weight Decay, Regularization

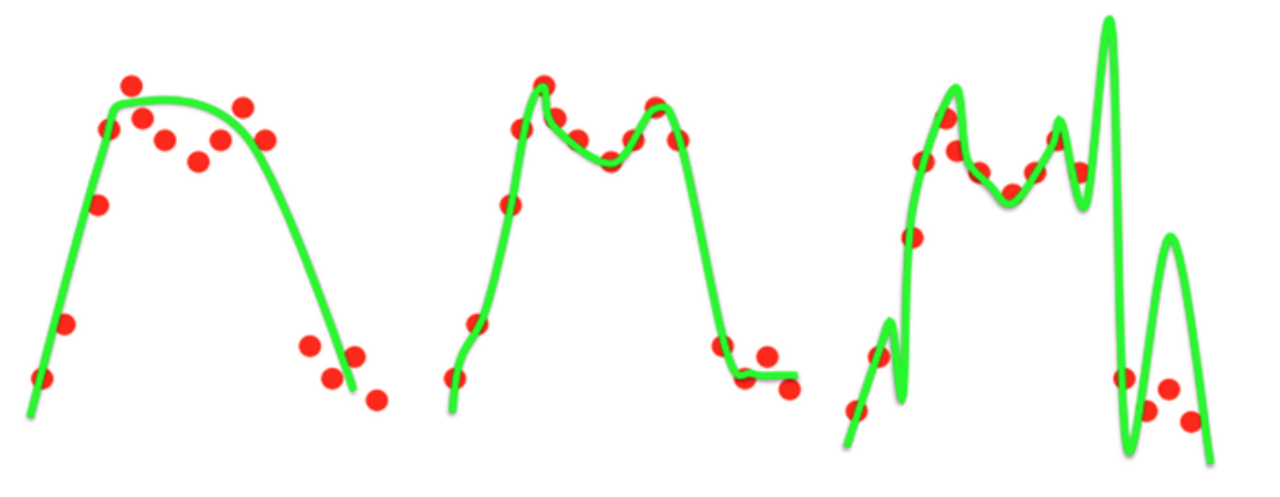
Overfitting

• 학습셋에 과하게 학습된 것, 일반화 성능이 떨어져 test score가 낮은 경우

• 원인: 적은 데이터셋 + 높은 복잡도의 모델 사용으로 모델이 학습셋을 외워버림

• 해결법: 모델 간소화, Early stopping, Weight decay, Dropout, Data augmentation

Underfitting

• 학습셋도 학습하지 못한 상태

• 원인: 낮은 Epoch, 낮은 복잡도의 모델, 적은 데이터셋 등

• 해결법: 더 학습하기? 복잡한 모델 사용하기? Data augmentation

Weight Decay (Regularization)

• 과적합을 방지하기위해 Loss function에 가중치가 커질 경우에 대한 패널티 항목을 집어넣어 학습된 모델의 복잡도를 줄임

L2 Regularization (Lidge)

• $L_{new}=L_{old}+\frac{\lambda}{2}(w_1^2+w_2^2+...+w_n^2)$

• 가장 일반적인 기법, 큰 값이 많이 존재하는 가중치에 제약을 주고 가중치 값들을 가능한 널리 퍼지도록 하는 효과, $\lambda$는 사용자 지정 하이퍼파라미터

• 다르게 쓰면 $Loss(w,x)=DataLoss(w,x)+\frac{\lambda}{2}||w||^2$

• 미분 시 $w\leftarrow w-\eta(\frac{\delta DataLoss}{\delta w}+\lambda w)=w(1-\eta\lambda)-\eta\frac{\delta DataLoss}{\delta w}$

• 기존 dataloss에 $\lambda w$를 더한 만큼 가중치가 보정됨, $w(1-LR*\lambda)$ 이므로 weight가 작은 factor에 비례감소하기 때문에 weight decay라고 불림

L1 Regularization (Lasso)

• $L_{new}=L_{old}+\lambda(|w_1|+|w_2|+...+|w_n|)$

• 기존 loss function에 파라미터의 절대값을 더해 적용, 파라미터를 sparse하게 (0에 가깝게) 만드는 특성

• L1, L2 동시에 사용도 가능 $L_{new}=L_{old}+\frac{\lambda_1}{2}W^TW+\lambda_2(|w_1|+|w_2|+...+|w_n|)$