이 글은 칸아카데미의 '선형대수학(Linear algebra)' 강의를 참고하여 작성하였습니다.
링크: Khan academy
Linear combinations and span
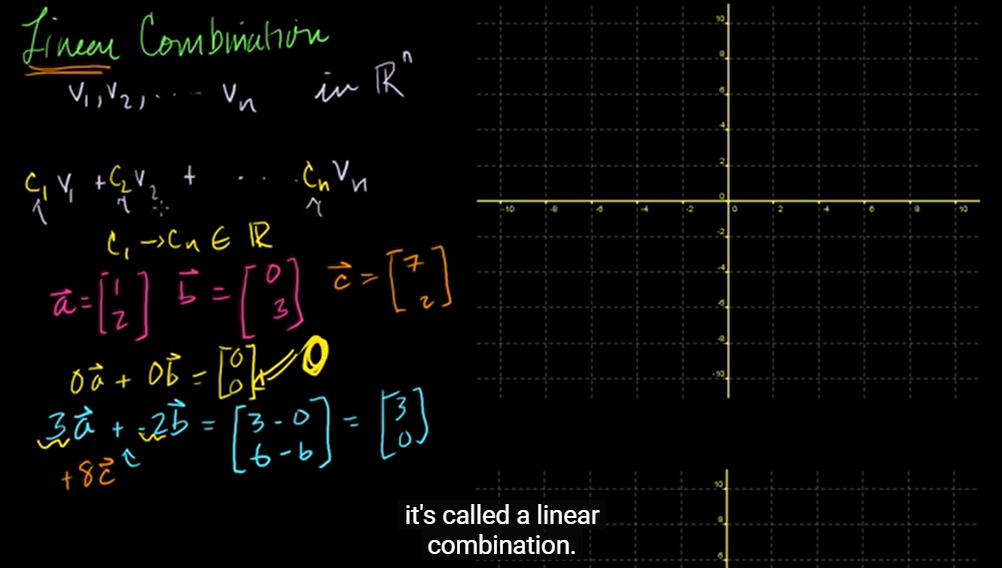
🌈 Linear combination이란?
선형 결합, 말 그대로 선형 직선들의 덧셈이다.
- + + +
- 스칼라값 c를 곱해준 벡터들의 합도 포괄하는 개념
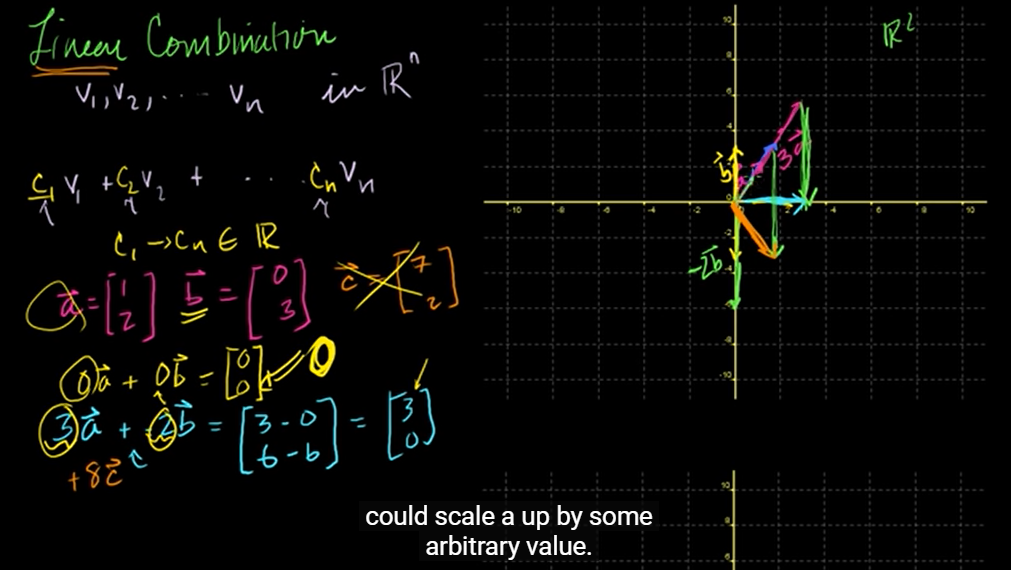
🌈 Why do you have to add that "Linear" prefix?
3 - 2는 단순히 벡터들을 scaling up(=increase)하는 것이다. 곱하거나 제곱하거나 한다면 비선형적으로 바뀔 수 있으나, 결합(덧셈)하기만 하는 것은 선형성에 아무런 영향을 미치지 않기 때문에 "Linear"라는 prefix를 Combination 앞에 꼭 붙여주는 것이다.
🌈 Can any two vectors represent anything in ?
We can fill up any point in with the combinations of a and b.
눈치챘을 수도 있겠지만, 평면에 존재하는 모든 값들은 벡터 a와 벡터 b의 조합으로 표현이 가능하다.
여기서 Span이라는 개념이 나온다.
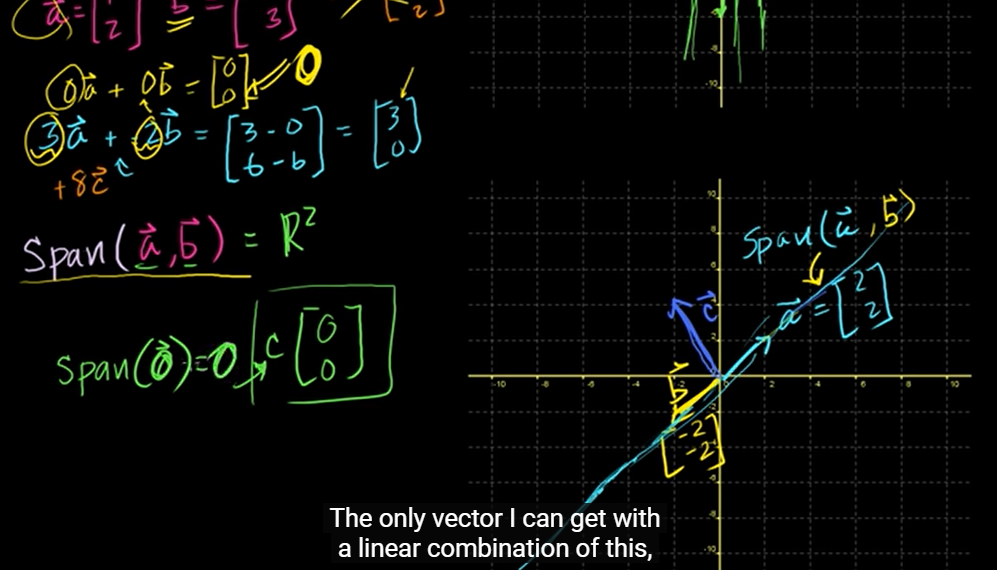 Span을 범위 또는 폭이라고 이해하면 된다.
Span을 범위 또는 폭이라고 이해하면 된다.
Span(, ) = 인 경우, 의 모든 값들을 벡터 a와 b가 표현할 수 있다.
✨그러나, 그렇지 않은 경우도 있음을 알고 있어야 한다.
=(2, 2), =(-2, -2)일 때,
아무리 scale up을 하더라도 오른쪽에 보이는 파란 직선 밖으로는 벗어날 수 없다.
즉, 아무 vector 2개를 골라 의 모든 값을 표현한다는 것이 항상 가능하지는 않다는 이야기다.
0 벡터일 때도 마찬가지다.
- Span()=0이기 때문에 어떠한 scalar 값(c)이 와도 항상 0이 된다.
- 모든 값을 표현할 수 없다.
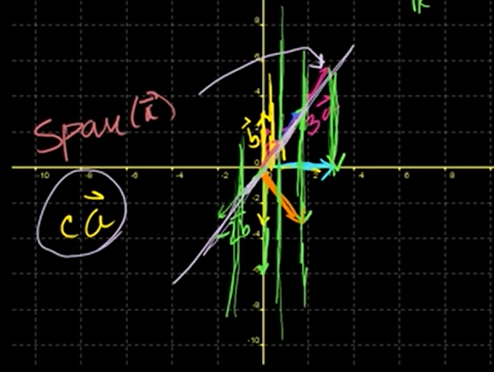
span()도 단순히 직선일 뿐.
c에서 c를 arbitrary한 값으로 지정할 때 아무리 직선에 스칼라 곱을 해준다고 해도 직선 밖으로는 벗어날 수 없다.
✨ Orthogonality?
- 기하학의 수직을 일반화한 용어
- 두 벡터의 내적이 0일 때, 다시 말해 이 둘이 직각을 이룰 때를 말한다.
 정리하자면,
정리하자면,
vector a, b spans
= any vector in can be represented by a linear combination of and
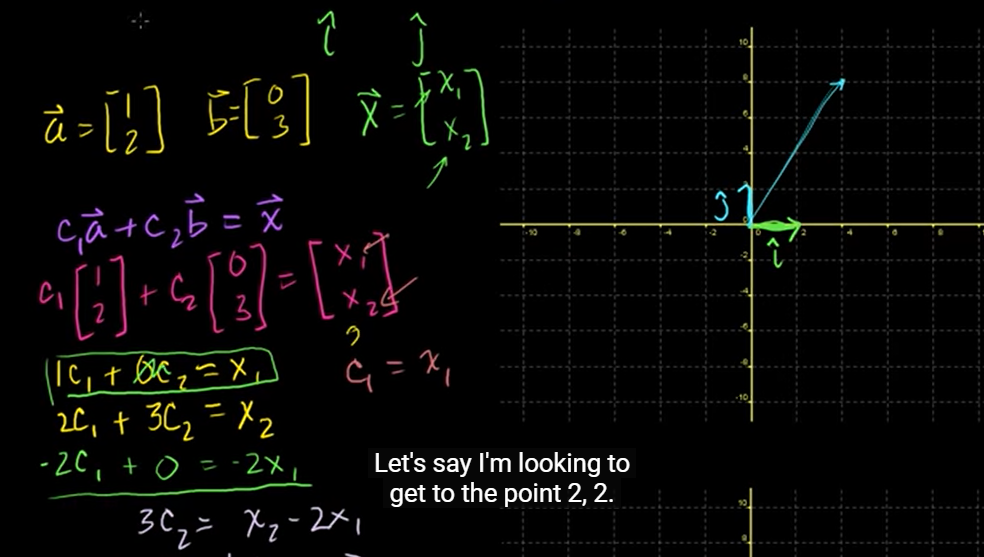 를 에 있는 아무 값 (, )라고 할 때,
를 에 있는 아무 값 (, )라고 할 때,
, 가 무엇이든 간에 , 가 위 이미지처럼 주어진다면 모든 값을 구할 수 있다.
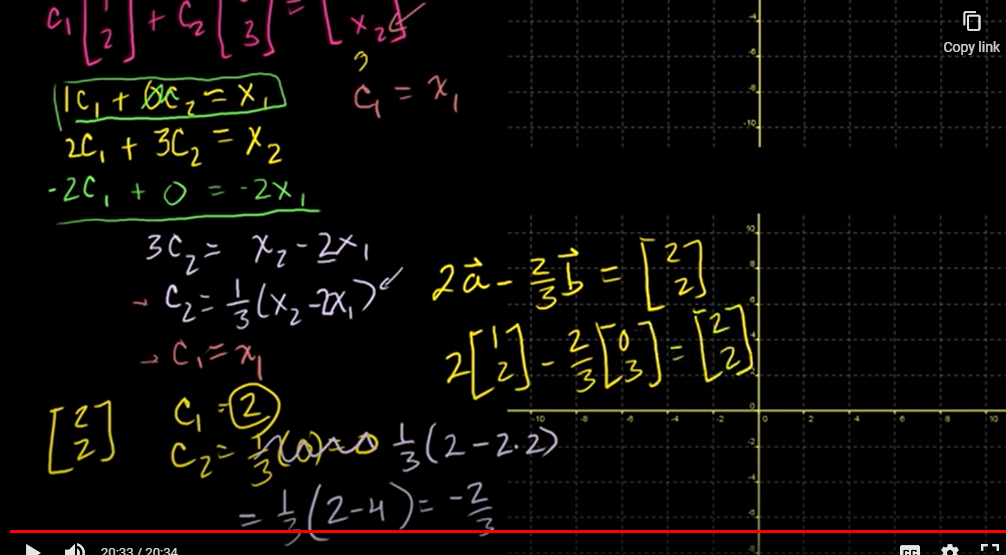 연립 방정식을 통해 , 을 구하면 된다.
연립 방정식을 통해 , 을 구하면 된다.
🌈 정리
- span은 벡터들의 선형결합으로 만들 수 있는 모든 영역을 말한다.
- 단, 두 개의 벡터는 '선형 독립적'이어야 한다.
- 0벡터가 만들 수 있는 영역은 자기 자신 뿐이다.
- 벡터 하나로는 직선만 만들 수 있다.

