Clustering - Hierarchical Agglomerative Clustering (HCA)

Hierarchical Agglomerative Clustering (HCA) is a method of cluster analysis which seeks to build a hierarchy of clusters. Because this is 'Agglomerative', we do this with 'bottom-up' approach

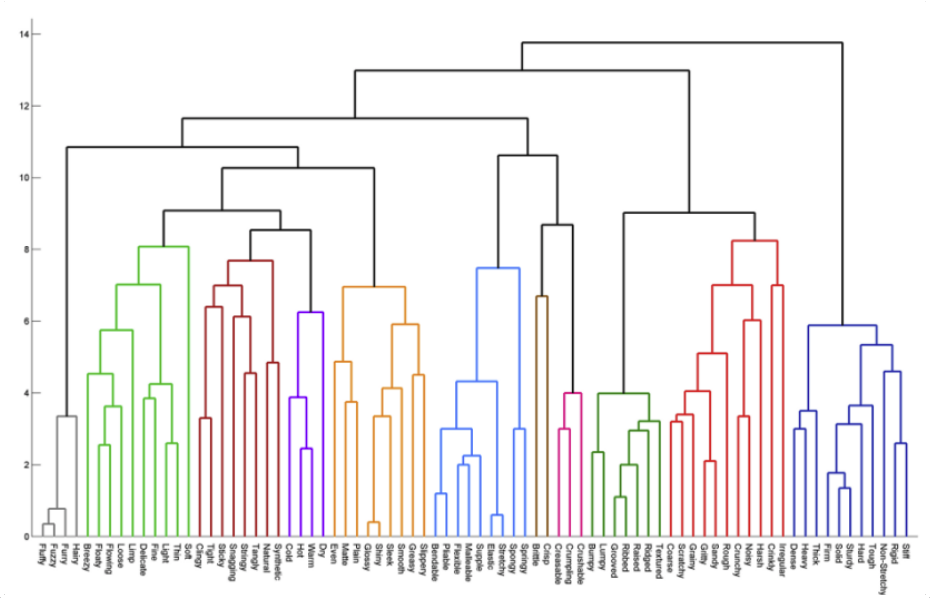
이미지 출처: https://ratsgo.github.io/machine%20learning/2017/04/18/HC/

• HCA는 상향식 계층 클러스터링이라고 부른다
  => 아래부터 위로 점차 데이터를 묶어나가기 때문
• 위와 같은 Dendrogram에서 x축은 데이터 하나하나를, y축은 유사도(유클리디안 거리)를 나타낸다
• 모든 데이터 사이의 유사도를 계산하기 때문에 속도는 매우 느림

Dendrogram & Algorithm

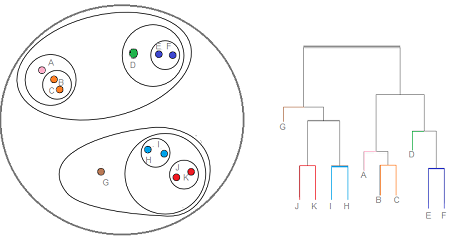
이미지 출처: https://www.statisticshowto.com/hierarchical-clustering/

1. 모든 데이터를 각자의 독립적인 클러스터로 세팅한다
2. 유사도(similarity)와 묶는 방식(linkage)을 정한다 (그림에서는 single로)
3. 가장 유사도가 높은 2개의 클러스터를 고른다
4. 정해진 방식으로 묶는다 (방식은 아래)
5. 모든 데이터가 묶여 하나의 클러스터가 될 때까지 반복한다. 모든 데이터가 묶이면 dendrogram을 그린다
6. Dendrogram에서 특정 거리를 기준으로 세로로 잘랐을 때, 나뉘는 클러스터들을 최종 클러스터로 선정한다

Linkage

1. Single : 가장 가까운 데이터 Pair가 포함된 2개의 클러스터를 합친다
2. Average : 클러스터 사이 평균 거리가 가장 가까운 2개의 클러스터를 합친다
3. Complete : 임의로 2개의 클러스터를 선택에 가장 멀리 있는 데이터간의 거리가 가장 가까운 2개의 클러스터를 합친다
4. Ward : 모든 클러스터들의 within cluster variance가 최소가 되는 클러스터들을 합친다
   => Within cluster variance : 클러스터 내부의 데이터간 sum-of-squared distance

장단점

장점

• 원하는 similarity와 linkage를 사용할 수 있어 다양한 공간에서 다양한 형태의 클러스터를 찾을 수 있다
• Dendrogram을 이용하여 데이터에 따라 유연하게 최적의 클러스터 개수를 정할 수 있다
• 어떤 linkage 방법을 사용하더라도 한번에 하나씩 클러스터가 줄어들기 때문에 원하는 클러스터 개수를 찾을 수 있다

단점

• K-means에 비해 매우 느리다 (대용량에 부적합 : O(N^3))