이번 포스트에서는 개인적으로 딥러닝에서 가장 중요하다 생각하는 loss function, optimizer중 loss function의 cross entropy를 설명하려합니다.
cross entropy를 알기 전 먼저 정보이론에 대해 알고 가겠습니다.
컴퓨터는 전기의 on/off 로만 무언가를 구분 합니다.
그러면 동전을 예로 들어 5번 동전을 던졌을 경우의 결과를 알려면 질문을 총 5번 하면 됩니다. 앞면을 0 뒷면을 1 이라 할때 10111 이런식으로 결과를 보내면 됩니다.
하지만 26가지 알파벳 중 어떤 알파벳인지 알고 싶으면 어떻게 해야할까요? 간단히 알파벳을 반으로 나눈 뒤 앞쪽에 속하는지 뒤쪽에 속하는지 알면 됩니다.
B를 예시로 앞에 속하면0 뒤에 속하면 1이라 할때
A B C D E F G H I J K L M / N O P Q R S T U V W X Y Z 0
A B C D E F / G H I J K L M 0
A B C / D E F 0
A B / C 0
A / B 1
B = 00001
이렇게 4번의 질문으로 한 글자를 추려 낼 수 있습니다 운이 좋다면 4 번도 가능합니다.
위 예시들을 봤을때 임을 알 수 있습니다.
위 설명한 알파벳의 경우 경우의 수가 26개이므로 이죠. 이하
그리고 이를 R.V.L Hartley가 라고 그의 논문에서 정립 했습니다.
H는 정보량, n은 문자의 개수, 즉 결과의 개수 입니다.
이제 entropy(불확실성)를 설명하겟습니다.
entropy의 수식은
= 입니다.
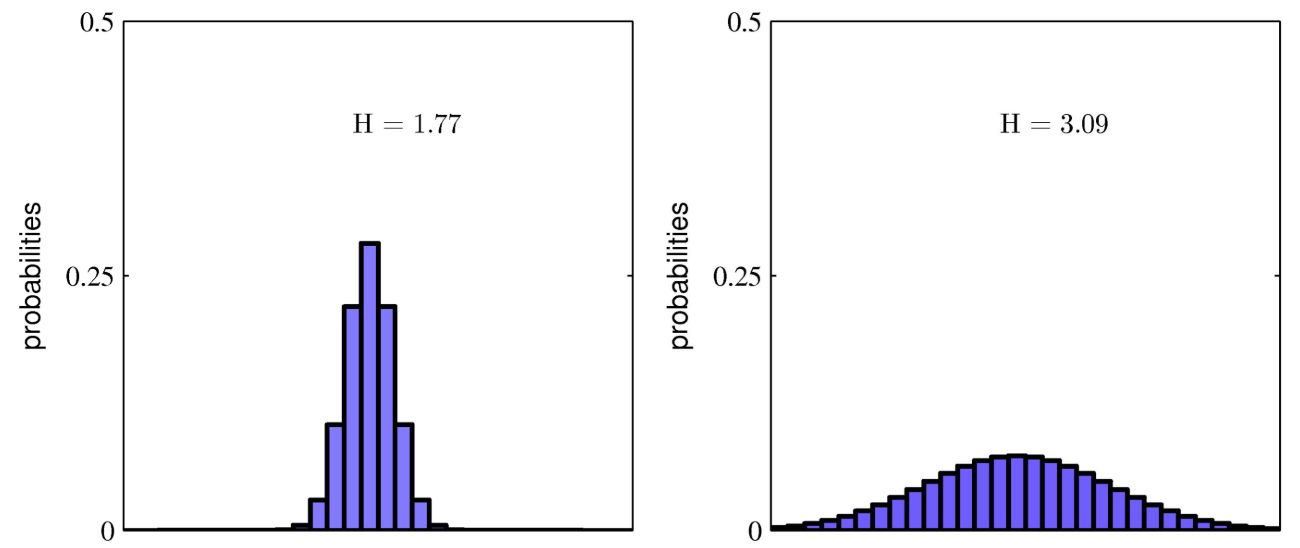
이는 확률 분포가 균등할수록 높게 나오는데 당연히 정육면체 주사위를 던져서 3이 나올 확률이 내일 아침 해가 서쪽에서 뜰 확률보다 불확실한걸 생각하면 간단히 이해 할수 있습니다.
이제 본론인 cross entropy입니다.
이것도 수식부터 빠르게 알아보자면
= 입니다.
p는 딥러닝에서 target one hot vector q는 모델의 output이라 생각하시면 됩니다
코드에서 p는 one hot 인덱스들이 q에는 확률 분포들이 들어가 있겟죠.
하지만 코드 말고 수학으로 돌아와 위 수식의 특성을 보여주기위해
# sample1
# sample2
#sample3
라 가정하고 위 수식에 대입하면
#sample1
#sample2
#sample3
log(q) = [-1,-3,-3,-2]
= 1.75
위에서 보이듯이 두 확률 분포가 같아질수록 cross entropy값은 낮아집니다.
이러한 이유때문에 머신러닝에서 자주쓰이는것이죠.
reference : https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html
