회귀란 일반적으로 데이터들을 2차원 공간에 찍은 후에 이들 데이터들을 가장 잘 설명하는 직선이나 곡선을 찾는 문제라고 할 수 있다.
y = f(x)에서 출력 y가 실수이고 입력 x도 실수일 때 함수 f(x)를 예측하는 것이 회귀이다.
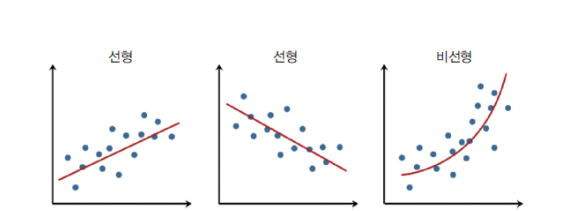
선형 회귀
선형 회귀의 기본식
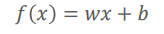
기울기 -> 가중치
절편 -> 바이어스
일차함수와 함수식이 같음.
다중 선형 회귀식 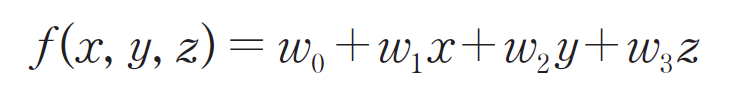
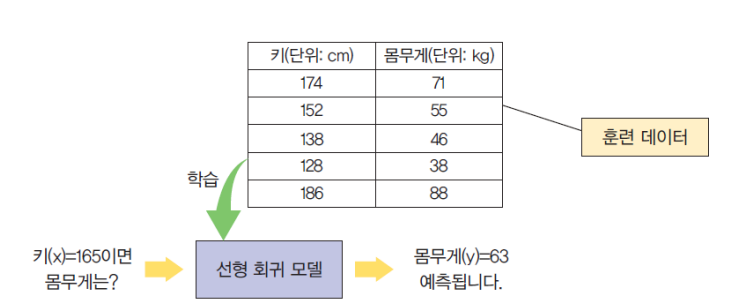
예제
종류
단순 선형 회귀
독립 변수(x)가 하나인 선형 회귀.
다중 선형 회귀
독립 변수가 여러 개인 경우