손실 함수(Loss Function)

What is loss function?

모델의 출력값과 사용자가 원하는 출력값의 오차

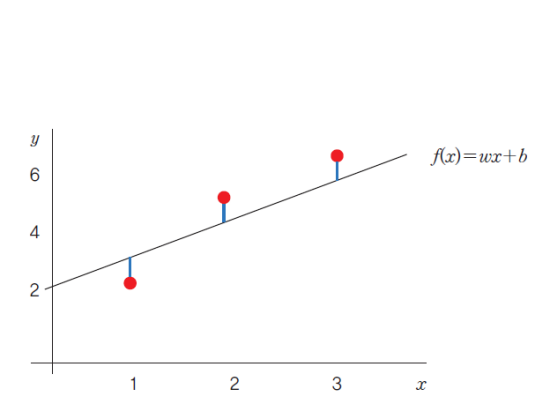
손실함수의 함수값이 최소화 되도록 하는 가중치(weight)와 편향(bias)를 찾는 것이 목표임

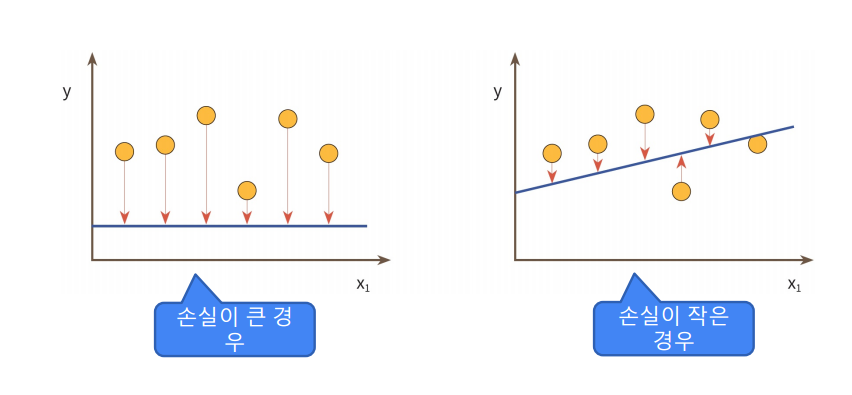
대표적인 손실 함수 종류

MSE(Mean Squared Error)

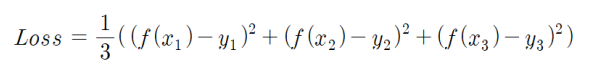
1. 각 점을 (x1, y1), (x2, y2)... 일 때 함수의 y값에 점의 y값을 빼서 제곱(음수를 제거하고 거리만을 보기 위함임)한다.

2. 전부 더하고 점의 개수만큼 나눠준다.

일반화

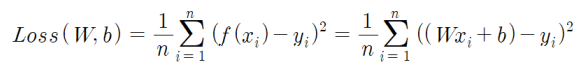
시그마로 합을 표현하고 f(X)에 함수식을 넣어 일반화

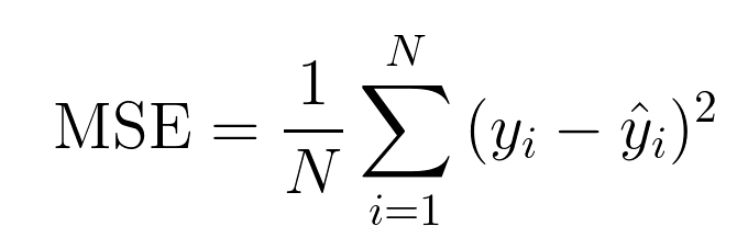
RMSE(Root Mean Squared Error)

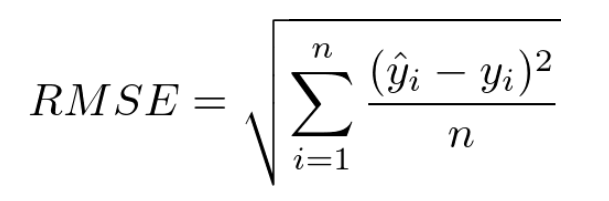
MSE에 제곱근을 씌운 것임.

Crossentropy란?
두 확률 분포 사이의 유사성 또는 차이를 측정하는 데 사용되며, 두 확률 분포 간의 차이를 정량화하는 방법이다.

Binary Crossentropy

모델의 예측과 실제 타겟(레이블) 간의 차이를 측정한다.

이진 분류(Binary Classification) 문제에서 주로 사용됨(=레이블 클래스가 2개일 때)

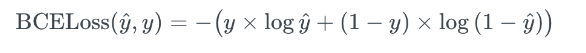
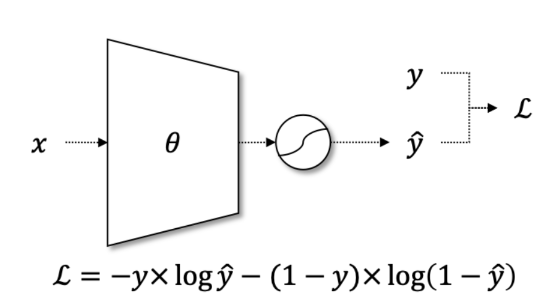
y는 실제 타겟(레이블) 값이다.(불연속적인 실제값)
y hat은 모델의 예측 확률을 뜻한다.(0 과 1 사이의 연속적인 시그모이드 함수 출력값을 의미함)

Categorical Crossentropy

모델의 예측 확률 분포와 실제 클래스(레이블) 분포 간의 차이를 측정한다.

다중 클래스 분류(Multi-Class Classification) 문제(2개 이상의 레이블 클래스일 때)에서 사용됨.

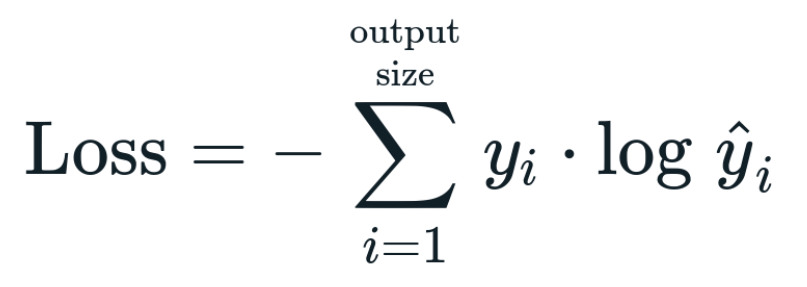
y_i는 실제 클래스 i의 확률 분포 값이다.
y hat_i는 모델의 예측 클래스 i의 확률 분포 값이다.

Sparse categorical crossentropy

다중 클래스 분류(Multi-Class Classification) 문제(2개 이상의 레이블 클래스일 때)에서 사용됨.

특히, 클래스 레이블이 원-핫 인코딩(One-Hot Encoding)이 아닌 정수 형태로 제공될 때 사용된다.
#그렇다고 정수 형태로 제공될 때만 사용되는 것은 아니다.

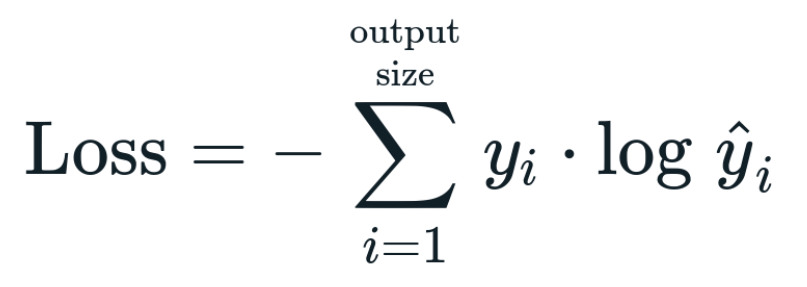
y_i는 실제 클래스 i의 확률 분포 값이다.
y hat_i는 모델의 예측 클래스 i의 확률 분포 값이다.

Sparse categorical crossentropy vs Categorical Crossentropy

둘은 공식이 같아 보이지만 y_i에서 차이가 있다. 
Categorical Crossentropy의 y_i는 원-핫 인코딩으로 표현되므
1또는0이지만, 
Sparse categorical crossentropy의 y_i는 정수로 표현되므로 1이다.

이 외에도 많은 함수가 있는 것을 볼 수 있다.