내가 생각한 convolution layer를 수행하기 위한 아키텍처는 2가지가 있는데 한가지는 구현이 쉽지만 효율이 떨어질 것으로 예상되는 것이고 다른 하나는 효율이 좋지만 구현이 어려울 것으로 예상되는 구조이다.
후자는 코드 작성에 들어가기에 몇가지 문제점이 남아있어서 이번에는 일단 전자의 방법을 채택해 NPU를 구현하기로 결정했다.
이번 포스팅에선 전자만 설명하고 후자는 나중에 다른 포스팅에서 설명하겠다.
input 데이터의 컨트롤 등은 해당 모듈이 아닌 npu 내에 존재하는 다른 모듈에서 수행할 예정이므로 해당 모듈은 input이 알맞게 들어오는 것을 가정하고 만들어졌음을 유의해주길 바란다.
첫번째 방법은 adder tree 방식을 응용한 아키텍처로 기존의 adder tree 방식에 D_FlipFlop과 8bit adder를 1개씩 추가한 아주 간단한 방법이다.
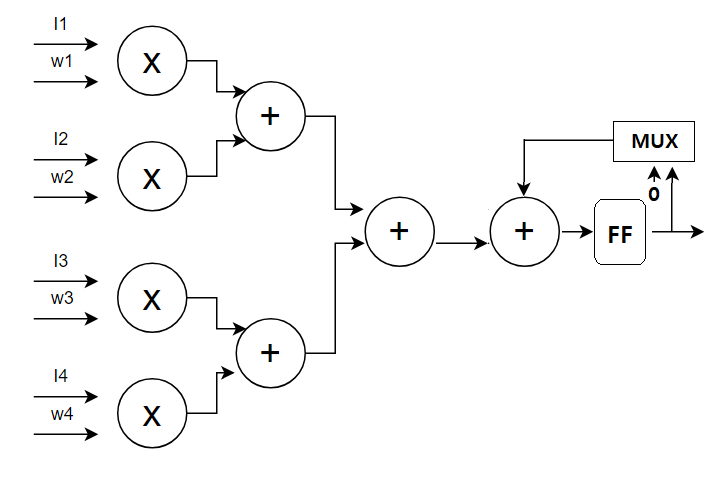
대략 이러한 구조를 가진다.
기존의 adder tree의 최종값이 덧셈기를 거쳐 FF에 저장되었다가 다음 사이클에 다시 덧셈기로 보내져 해당 사이클의 adder tree의 최종값에 더해진다.
무한정 더해지는 것은 아니고 mux에 의해 FF에 저장된 값이 덧셈기로 보내져서 더해지느냐 아니면 그냥 0을 보내서 아무것도 더해지지 않게하냐가 결정된다.
작동방식을 설명하자면 일단 곱셈기가 그림처럼 4개가 아니라 9개로 구성되어 있다고 하자.
그렇다면 1 사이클에 9개의 input과 9개의 weight의 곱셈의 합을 구할 수 있다.
만약 3*3 필터 즉 9개의 input과 9개의 weight의 결과값을 구하는 것은 1사이클만에 수행할 수 있다. 그러니 mux는 계속 0을 adder로 보내 adder tree의 값에 따로 다른 값을 더하지 않고 그대로 출력한다.
4*4 필터를 수행할 때는 이와 다른데 16개의 input, weight에 대해 계산해야하므로 총 2 사이클이 필요하다. 그러므로 mux는 0과 FF에 저장된 값을 번갈아보네 2 사이클마다 유효한 값이 출력되도록 한다.
각 사이클의 곱셈기의 input, FF의 input, output들을 간단하게 나타내면
(1사이클) (input0~7, weight0~7) (tree_out1+0=tree_out1) (0, 무효)
(2사이클) (input8~15, weight8~15) (tree_out2+tree_out1) (tree_out1, 무효)
(3사이클) (input16~23, weight0~7) (tree_out3+0=tree_out3) (tree_out2+tree_out1, 유효)
(4사이클) (input24~31, weight8~15) (tree_out4+tree_out3) (tree_out3, 무효)
(5사이클) (input32~39, weight0~7) (tree_out5+0=tree_out5) (tree_out4+tree_out3, 유효)
가 되어 1사이클 이후로 2사이클마다 유효한 값을 출력한다.
비슷하게 3*3*3 혹은 5*5의 경우 input, weight의 수가 19~27사이이므로 mux가 (0->FF->FF->0->FF->FF)을 반복해 출력하면 결과적으로 3사이클마다 유효한 값이 나온다.
이렇게 쓰이는 필터의 종류에 따라 덧셈을 몇사이클 진행할지만 조정한다면 여러가지 필터에 대해서도 효율성을 유지하면서 연산을 할 수 있다.
weight의 개수에 따른 계산 효율, 즉 유효한 곱셈기의 이용율은 다음과 같다.
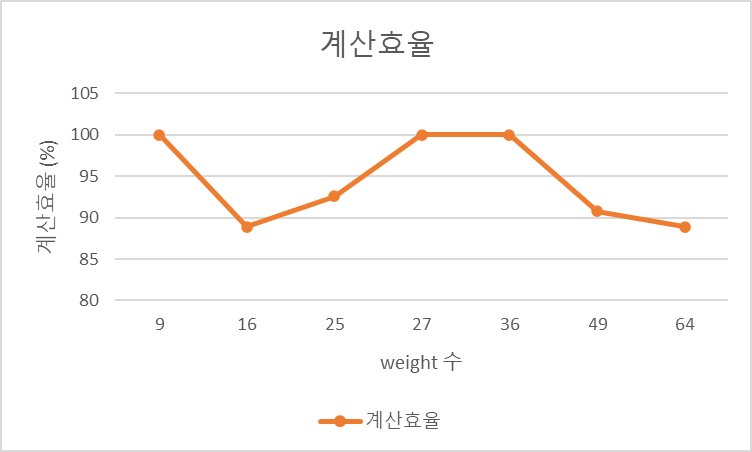
3*3 ~ 8*8, 3*3*3, 4*4*4 필터들에 대한 계산 효율을 나타낸 그래프이다. 많은 신경망에서 자주 쓰이는 3*3 필터에서 높은 효율을 보이고 그외의 경우에도 90%가량의 효율을 유지한다.
또한 여러 stride 값에 대해서도 그에 맞게 input을 입력하기만 하면 되기에 아무런 문제없이 대응 가능하다.
NPU에 해당 계산유닛을 1개만 배치하는게 아니라 총 8개를 배치할 예정인데 해당 유닛들은 같은 input을 공유하지만 다른 weight값을 입력받는다. 즉 유닛들이 각각 다른 채널의 컨볼루션을 진행한다고 할 수 있다.
이는 input의 데이터가 dram에 저장되어있다고 가정했을 때 1개의 채널을 전부 수행한 후 다른 채널을 시작하는 방식의 경우 채널의 수만큼 input을 불러와야하므로 비효율적이기 때문이다.
여러개의 유닛을 배치해 input을 동시에 공유시킨다면 systolic array 방식처럼 각 유닛마다 따로 input을 저장하기위한 레지스터를 추가할 필요없이 여러 채널에 대한 연산을 동시에 수행할 수 있으므로 효율적이다.
굳이 8개를 배치한 이유는 조사결과 대부분의 신경망에서 채널의 수가 8의 배수에 가까웠기 때문이다.
컨볼루션을 어떻게 수행할 것인지는 사용자가 input과 weight를 어떻게 주느냐에 따라 달라지는데
예를 들어서 8개의 채널에 대한 컨볼루션을 모두 끝마치고 그 다음 8개 채널을 다시 컨볼루션하고 싶다면 (설명의 용이를 위해 3*3=9개의 weight를 가진 필터로 가정하자) weight를 고정한채로 input을 순서에 맞게 입력시켜주면 된다.
하지만 반대로 input을 여러번 불러오는 것을 최소화하고 싶다면 input을 고정한채로 weight를 변경하면 된다.
즉 input을 고정하고 1사이클에서 0~7 채널의 필터의 weight를 입력하고 2사이클에서 8~15 채널의 weight를 입력하면 된다.
이렇게 하면 같은 input을 사용하는 모든 채널을 계산하기위해 한번만 input을 불러오면 된다.
이후 maxpooling까지 한번에 수행하고 싶다면 maxpooling이 2*2=4개의 output을 필요로 하므로 그에맞게 4종류의 input을 번갈아 입력하고 4사이클마다 weight를 바꿔주면 된다.
각 사이클에서의 input과 output을 설명하자면
(1사이클) (input set 0, channel 0~7) (output0 of channel 0~7)
(2사이클) (input set 1, channel 0~7) (output1 of channel 0~7)
(3사이클) (input set 2, channel 0~7) (output2 of channel 0~7)
(4사이클) (input set 3, channel 0~7) (output3 of channel 0~7)
-> maxpooling output of channel 0~7
(5사이클) (input set 0, channel 8~15) (output0 of channel 8~15)
(6사이클) (input set 1, channel 8~15) (output1 of channel 8~15)
(7사이클) (input set 2, channel 8~15) (output2 of channel 8~15)
(8사이클) (input set 3, channel 8~15) (output3 of channel 8~15)
-> maxpooling output of channel 8~15
이런 식으로 input set0~3과 channel들의 weight가 캐시에 저장되어 있다면 dram을 여러번 참조할 필요가 없다.
이 첫번째 방법은 input의 크기, weight의 개수, stride, 필터의 개수 등 여러 요인에 상관없이 효율을 유지하며 계산할 수 있다는 장점이 있다.
다만 구조상 곱셈기->덧셈기로 이어지는 구간에서 상당히 긴 critical path가 생길 것으로 예상하는데 추가로 면적을 차지하는 pipelining을 피하기 위해서는 효율이 높은 곱셈기와 덧셈기를 사용해야한다는 기존의 adder tree 방식과 같은 단점이 있다.
일단 코드 작성에서 곱셈기와 덧셈기는 간단한 형태를 사용했는데 그 이유는 일단 아키텍처가 제대로 작동하는 지, 다른 방식에 비해 무엇이 나은지를 판단하는 것이 우선이기 때문이다. 효율적인 곱셈기, 덧셈기를 설계해서 사용해도 다른 아키텍처에서 이들을 똑같이 써버리면 차이점이 없어진다.
또한 효율적인 곱셈기, 덧셈기를 설계하는 것은 그 자체만으로도 상당한 난이도가 있다고 생각했기에 이들을 일단 뒤로 미루고 아키텍처를 완성하는 것을 우선했다.
convolution을 수행하는 모듈에 대한 설명은 이것으로 끝이다. 다음 포스팅에서는 relu 함수와 maxpooling을 수행하는 모듈을 설명할 예정이다.