k-means clustering

주어진 데이터를 k개의 군집으로 묶는 알고리즘으로

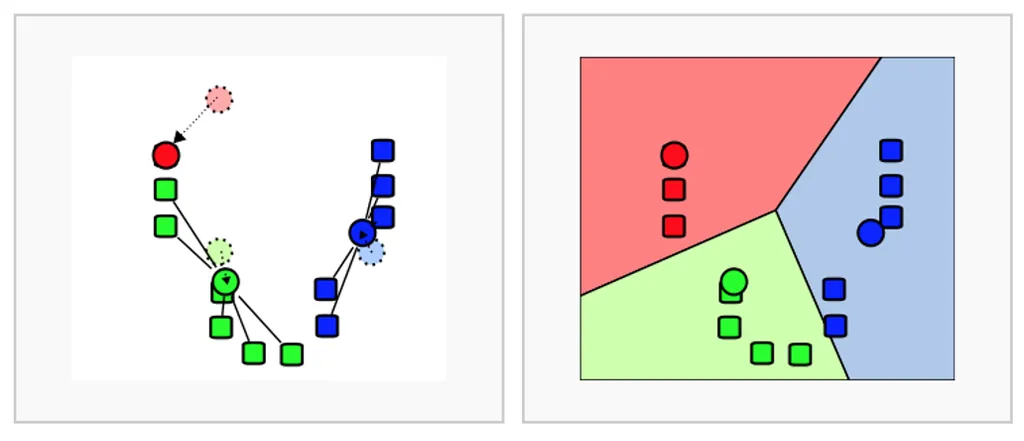
수행 순서

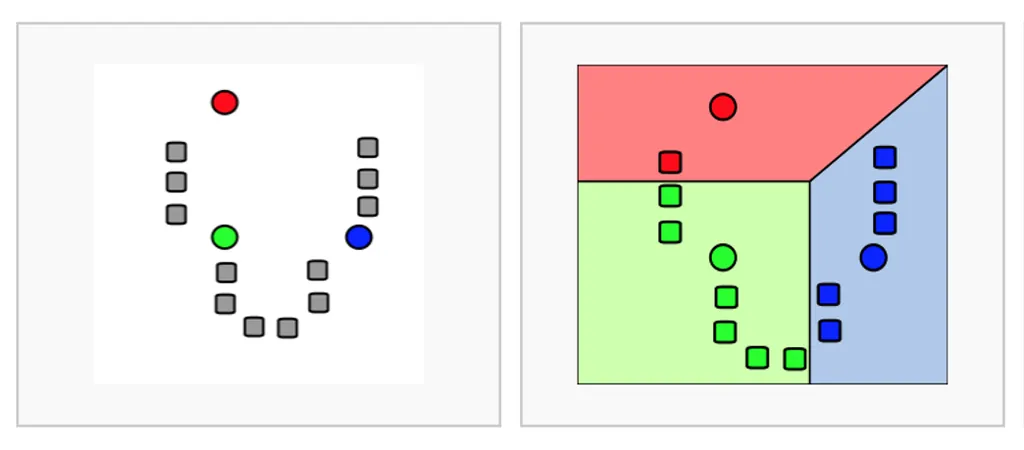
1. 순집 수 설정(K개)
2. 임의의 중심점 선정
3. 각 데이터를 가장 가까운 중심점에 할당하여 그룹화
4. 각 클러스터의 새로운 중심점 재계산
5. 3-4번을 클러스터의 중심이 더 이상 변하지 않을 때까지 반복

K 값

K 값이 너무 작다면

• 데이터가 과도하게 일반화
  ex) 단 두 집단으로 Iris 데이터를 군집화하기

K 값이 너무 크다면

• 클러스터가 세분화되어 무의미해질 수 있음
  ex) Iris 군집은 4개인데 8개로 군집화하면 의미X
  
  

엘보우 기법

클러스터의 개수에 따른 SSE(Sum of Squared Error) 값을 시각화하여 적절한 K의 값을 찾는 방법

• SSE: 클러스터의 중심과 각 데이터포인트 간의 거리의 제곱합
• 클러스터의 개수가 커질수록 SSE는 감소한다.
• 엘보우 포인트: SSE가 급격히 감소하다가 완만해지는 지점. 이 값을 최적의 K로 간주한다.

def elbow(data, length):
    sse = [] # sum of squre error 오차제곱합
    for i in range(1, length):
        kmeans = KMeans(n_clusters=i)
        kmeans.fit(data)
        # SSE 값 저장
        sse.append(kmeans.inertia_)
    plt.plot(range(1, length), sse, 'bo-')
    plt.title("elbow method")
    plt.xlabel("number of clusters")
    plt.ylabel("SSE")
    plt.show()
    
elbow(points, 10)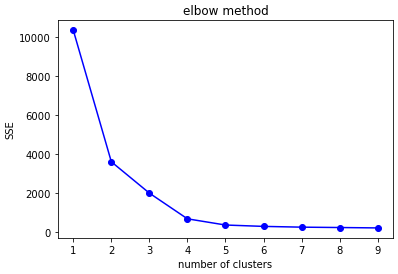

장점

• 일반적이고 적용하기 쉬움

단점

• 거리 기반으로 가까움을 측정하기 때문에 차원이 많을수록 정확도가 떨어짐
• 반복 횟수가 많을수록 소요 시간 증가
• 몇 개의 군집을 선정할지 사용자가 정해야 함 (주관적)
• 평균을 이용하기 때문에 이상치에 취약함

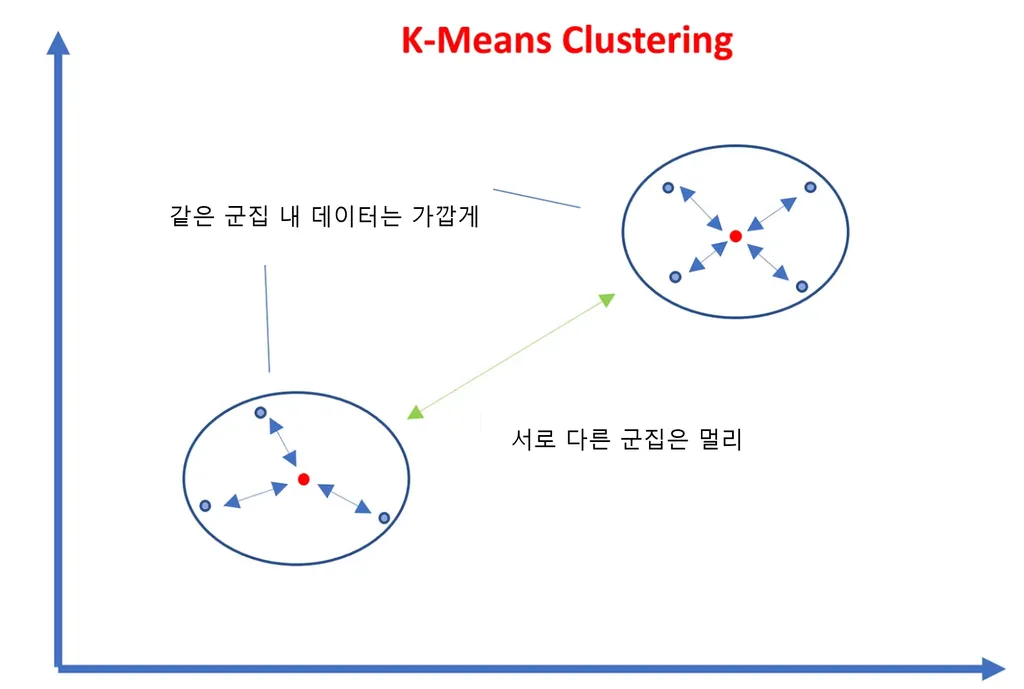
평가지표 - 실루엣 계수 Silhouette Analysis

군집화가 잘 되어있다는 것은 다른 군집과는 멀리 떨어져있고, 동일한 군집끼리는 가까이 있다는 의미.
실루엣 계수: 군집간의 거리가 얼마나 효율적으로 분리되어 있는지 측정한 값.

• $a(i)$: 데이터 포인트 $i$와 같은 군집에 속한 다른 포인트들과의 평균 거리
• $b(i)$: 데이터 포인트 $i$와 가장 가까운 다른 군집간의 평균 거리
• 정규화를 위해 $a(i)$와 $b(i)$ 중 큰 값으로 나눠준다.

$b(i)$가 클수록, $a(i)$가 작을수록 군집화가 잘 된 것이므로
실루엣 계수가 1로 갈수록 군집화가 잘 되어있고, -1에 가까울수록 잘못 군집화 되어있음을 의미

실습

• sklearn.cluster.KMeans
  • 함수 입력 값
    • n_cluster: 군집화 갯수
    • max_iter: 최대 반복 횟수
  • 메소드
    • labels_: 각 데이터 포인트가 속한 군집 중심점 레이블
    • cluster_centers: 각 군집 중심점의 좌표

• sklearn.metrics.sihouette_score: 전제 데이터의 실루엣 계수 평균 값 반환
  • 함수 입력 값
    • X: 데이터 세트
    • labels: 레이블
    • metrics: 측정 기준 기본은 euclidean

데이터 불러와서 확인

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

iris_df = sns.load_dataset('iris')

sns.scatterplot(data = iris_df, x = 'sepal_length', y = 'sepal_width', hue = 'species')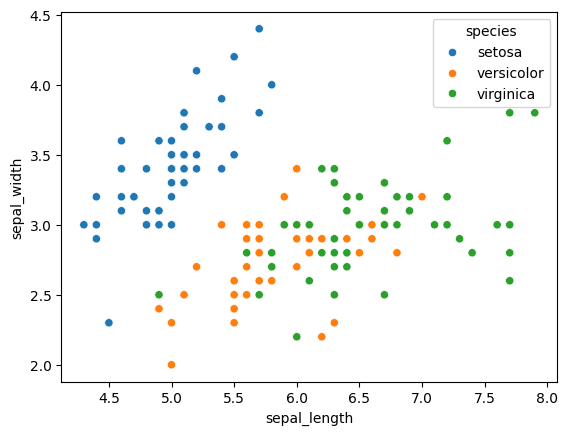

모델 학습시키기

iris_df2 = iris_df[['sepal_length','sepal_width','petal_length','petal_width']]

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 3, init = 'k-means++', max_iter = 300, random_state= 42)
kmeans.fit(iris_df2)

kmeans.labels_
# 예측 결과:
''' array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
      1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 0, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 0, 2, 0, 0, 0, 0, 2, 0, 0, 0,
       0, 0, 0, 2, 2, 0, 0, 0, 0, 2, 0, 2, 0, 2, 0, 0, 2, 2, 0, 0, 0, 0,
       0, 2, 0, 0, 0, 0, 2, 0, 0, 0, 2, 0, 0, 0, 2, 0, 0, 2], dtype=int32)'''

예측 결과 확인

iris_df2['target'] = iris_df['species'] # 정답
iris_df2['cluster'] = kmeans.labels_ # 예측
iris_df2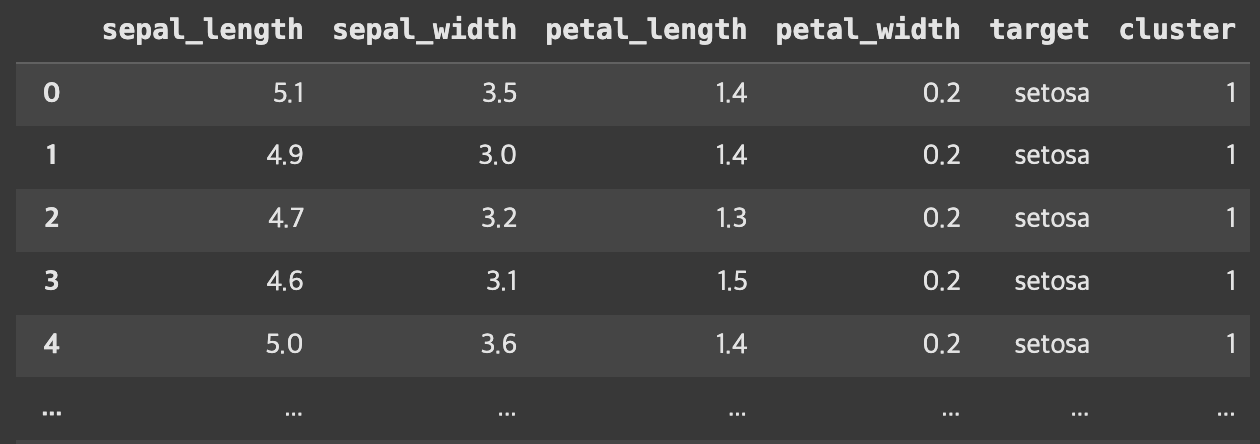

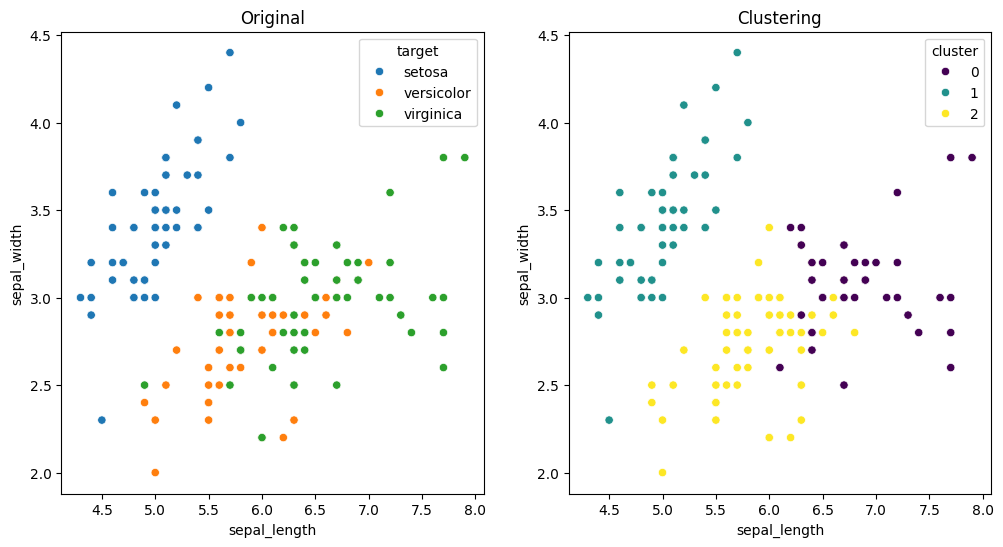
시각화하여 비교하기

plt.figure(figsize = (12,6))
plt.subplot(1,2,1)
sns.scatterplot(data = iris_df2, x = 'sepal_length', y = 'sepal_width', hue = 'target')
plt.title('Original')

plt.subplot(1,2,2)
sns.scatterplot(data = iris_df2, x = 'sepal_length', y = 'sepal_width', hue = 'cluster', palette= 'viridis')
plt.title('Clustering')
plt.show()