머신러닝 회귀 모델의 성능 평가 지표 (MAE, MSE, RMSE, R-squred)

회귀모델을 평가하는 평가지표

회귀모델은 그 모델이 잘 학습되어졌는지 확인하기 위한 회귀모델의 평가지표들이 4가지 있다. 이를 하나씩 살펴보자.

MAE(Mean Absolute Error)

• 모델의 예측값과 실제값의 차이의 절대값의 평균

• 절대값을 취하기 때문에 가장 직관적으로 알 수 있는 지표이다. (해석에 용이하다.)

• 절대값을 취하기 때문에 모델이 Underperformance(실제보다 낮은 값으로 예측)인지 Overperformance(실제보다 높은 값으로 예측)인지 알 수 없다.

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y, y_pred)

MSE(Mean Squared Error)

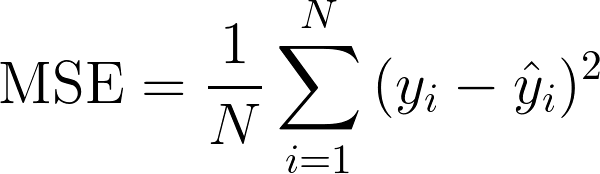
• 제곱을 하기 때문에 MAE와는 다르게 모델의 예측값과 실제값 차이의 면적의(제곱)합이다.

• 제곱을 하기 때문에 특이치(Outlier)에 민감하다.

from sklearn.metrics import mean_squared_error
mean_squared_error(y, y_pred)

RMSE(Root Mean Squared Error)

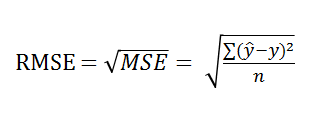
• MSE에 루트를 씌워 사용한다.

• RMSE를 사용하면 오류 지표를 실제값과 유사한 단위로 다시 변환하여 해석을 쉽게한다.

• 예측 대상의 크기에 영향을 바로 받는다.

• MAE보다 특이치에 Robust(강하다)하다.

from sklearn.metrics import mean_squared_error
rmse = mse**0.5

예시 네이버 주가와 삼성전자 주가

• 삼성전자의 주가 : 2,389,000원
• NAVER의 주가 : 778,000원

1. 삼성전자의 주가를 예측하는 모델을 만들었다고 가정하자.
   ➡ 만든 모델로 삼성전자 주가를 예측해보았더니, RMSE가 500,000이 나왔다
2. NAVER의 주가를 예측하는 모델을 만들었다고 가정하자
   ➡ 만든 모델로 NAVER 주가를 예측해보았더니, RMSE가 놀랍게도 똑같이 500,000이 나왔다

이 두 모델은 동일한 성능을 가지고 있는걸까?

분명 명확하게 이상한 점이 느껴진다. 삼성전자의 500,000와 NAVER의 500,000은 다르다.

에러가 예측하려는 값의 크기에 의존적이라는 면에서 RMSE는 크기 의존적 에러에 속하게 된다.

R-squared (Coefficient of determination, 결정계수)

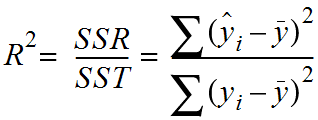
• SSE(Sum of Squares Error, 관측치와 예측치 차이)

• SSR(Sum of Squares Regression, 예측치와 평균 차이)

• SST(Sum of Squares Total, 관측치와 평균 차이)

R-squared는 현재 사용하고 있는 x변수가 y변수의 분산을 얼마나 줄였는가 이다.
단순히 y평균값 모델(기준모델)을 사용했을 때 대비 우리가 가진 x변수를 사용함으로서 얻는 성능 향상의 정도이다.

즉, R-squared 값이 1에 가까우면 데이터를 잘 설명하는 모델이고 0에 가까울수록 설명을 못하는 모델이라고 생각할 수 있다.

from sklearn.metrics import r2_score
r2 = r2_score(y, y_pred)

MAE vs RMSE

자, MAE와 RMSE 수학 공식을 자세히 살펴보자. 무언가가 비슷해보이지 않나..?

분명 중학교였나 고등학교 수학시간에 |X-Y| = (X-Y$)^2$이라고 배웠어서 나는 두 평가지표 사이의 차이점이 궁금해졌다.

예를 들어보자.

• 독립변수 = 주택의 노후도, 지하철 역과의 거리, 방 개수, 평수
• 종속변수 = 집 값

이러한 상황이라면, 회귀 예측값이 집값이므로 200,000($), 470,000($) 등으로 현실적인 값을 갖게 된다.

이 때 "이 모델을 쓰면 집값 계산에 있어서 200$ 정도 틀리는군. 예산에 ±200$ 정도는 각오 해야겠어"라는 직관적인 판단을 할 수 있는 평가 지표를 쓰면 좋지 않을까?

MSE는 잔차값을 절대값 취하고 평균 낸 것이다.

위 표를 통해서라면 이 모델이 평균 25,200$씩 틀리는 모델이라는 걸 알 수 있다.

그러나 RMSE를 쓰면 잔차 계산이 조금씩 난해해진다.

먼저, MAE와 RMSE의 차이점을 비교해보자.

1. 잔차를 제곱하고 다 더한 뒤 루트를 씌웠다는 점

2. 평균을 낼 때 $1/n$ 처리를 하는 게 아니라 $1/sqrt(n)$처리를 한다는 것

• 분모에 n보다 더 작은 sqrt(n)을 썼고, 분모가 작아지니 총 결과는 MAE보다 커진다.

그 결과 다음과 같은 차이가 발생한다.

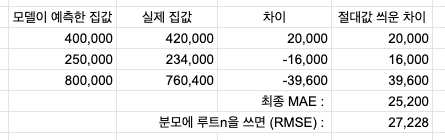
RMSE로 구한 에러값 27,228을 통해 "이 모델은 27,228$만큼 틀린 모델이다"라고 표현할 수는 없다.
이미 실생활에서 쓰는 계산법을 벗어났기 때문이다.

그렇다면 왜 직관적이고 좋은 MAE가 아닌 RMSE를 쓰는걸까?

결론부터 말하자면, RMSE는 "큰 오류값 차이에 대해서 크게 패널티를 주는 이점"이 있기 때문이다.

다시 위 집 값 예측 예시에서 한 가지 케이스를 추가해보자.

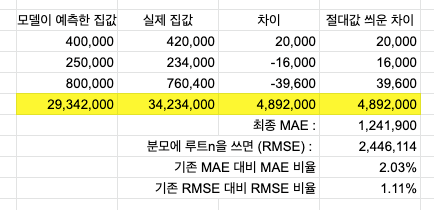
4번째 집 값 데이터가 추가되었다. 다른 데이터와는 다르게 깡패 수준의 스케일을 가지고 있다.
모델은 나름 최선을 다해서 가격을 예측했지만, 잔차(차이)는 4백만$ 수준이나 나와버렸다..
이런 현상을 "큰 오류값이 났을 때"라고 볼 수 있다.

이 때 집 값을 3개만 예측했을 때와 큰 오류값이 추가됐을 때 MAE와 RMSE의 비율을 비교해보자.

MAE가 약 2%의 비율을 가질 때 RMSE는 절반 수준인 1.11%를 갖게 된다.
큰 오류가 나타났어도 RMSE는 제법 방어를 잘 해냈다고 이해하면 된다.

이는 RMSE가 MAE와의 차이 중 첫번째였던, "잔차를 제곱하고 다 더한 뒤 루트를 씌웠다는 점"을 통해 큰 오류값에 패널티를 크게 주었기 때문에 가능하다.

머신러닝의 '학습'에 있어서는 이러한 특이값에 휘둘리지 않는 게 굉장히 중요하다.

정리하자면,
RMSE는 MAE에 비해 직관성은 떨어지지만 Robust한 성격(극단적이지 않은 성격)에서 강점을 보인다.

출처
https://velog.io/@ljs7463/%ED%9A%8C%EA%B7%80%EB%AA%A8%EB%8D%B8-%ED%8F%89%EA%B0%80%EC%A7%80%ED%91%9Cevaluation-metrics
https://velog.io/@tyhlife/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%ED%9A%8C%EA%B7%80-%EB%AA%A8%EB%8D%B8%EC%9D%98-%ED%8F%89%EA%B0%80-%EC%A7%80%ED%91%9C