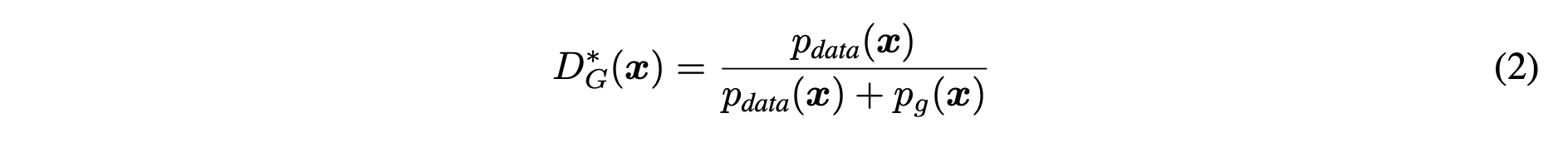GAN으로 유명한 다음의 논문을 읽고 학습한 내용입니다.
공부하며 작성한 내용이니 틀린 부분 지적해 주시면 감사하겠습니다!

Papers: 논문 링크

아래에 첨부된 이미지들의 출처는 위의 논문입니다.

논문의 구현은 다음의 링크에서 확인할 수 있습니다.
github

GAN 이란?

이번에 학습할 논문은 GAN 입니다.

이 논문에서는 generative model G와, discriminative model D를 동시에 학습하여 데이터를 생성하는 새로운 생성모델의 framework를 제안했습니다.

여기서 “생성모델”이란 실제로는 존재하지 않지만, 그럴싸한 데이터를 만들어 내는 모델을 의미합니다.

위 이미지에서 가장 오른쪽의 노란 박스가 쳐진 이미지만 실제 데이터이고,
왼쪽의 이미지들은 GAN을 통해 생성한 이미지입니다.
논문에서는 위의 이미지들에 대해 잘 나온것만 골라서 표시한게 아니고, (not cherry-picked)
실제 랜덤하게 추출했음을 밝히고 있습니다.(fair random draws)

이러한 생성 모델은 기존 데이터의 분포를 근사하는 것을 목표로 학습됩니다.

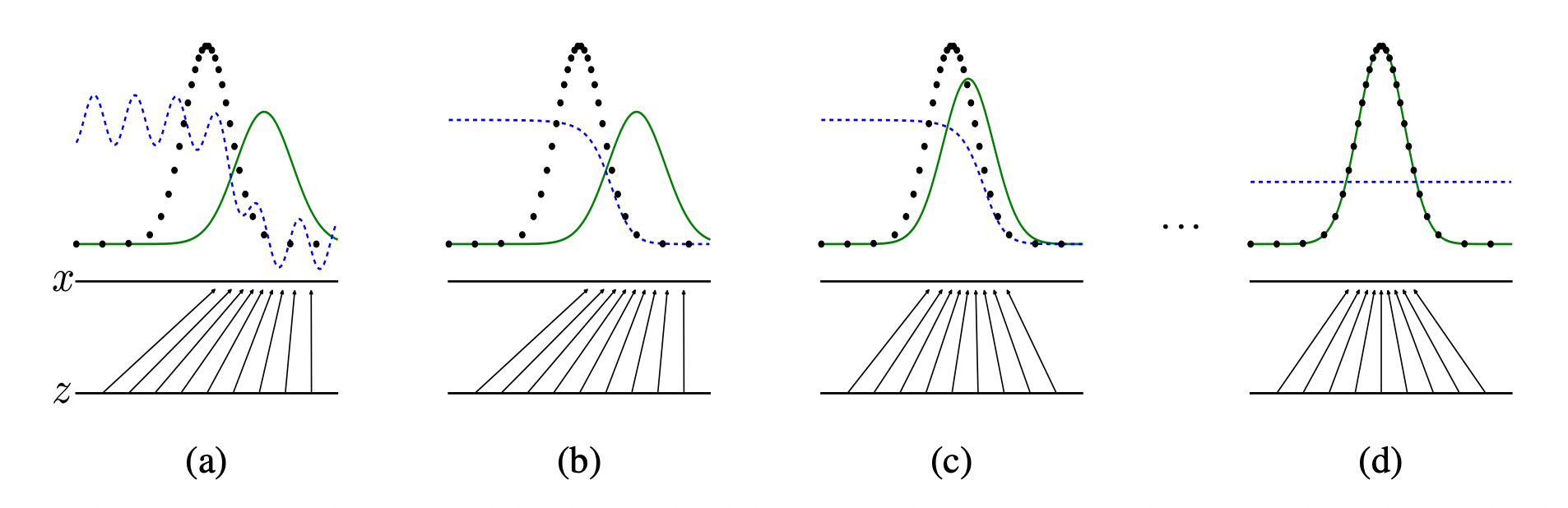
위 그림에서 볼 수 있듯, 생성모델의 데이터 분포(초록색 실선)가 학습이 거듭됨에 따라 원본 데이터의 분포(검은색 점선)를 따라가고, 생성 모델의 도메인 $z$가 $x$로 매핑됨을 볼 수 있습니다.

이렇게 모델이 잘 학습 되었다고 가정할 때,
생성모델의 분포에서 검은색 점이 아닌 데이터를 뽑아낸다면, 이 데이터는 실제로는 존재 하지 않는 생성된 데이터가 되는 것입니다.

이 논문 Generative Adversarial Networks(GAN) 이후 많은 후속 논문들이 나왔습니다.

Generative Adversarial Networks(GAN)

앞서 언급한대로, GAN은 다음 두개의 네트워크를 활용합니다.

• Generative model G
• Discriminative model D

또한 논문의 제목에서 볼 수 있는 Adversarial은 “적대적인” 이라는 뜻을 갖고 있습니다.
즉, 위의 두 네트워크가 서로 적대적으로 경쟁하며 발전하게 됩니다.
논문에서는 이를 minimax two-player game 이라고 표현하고 있습니다.

이제 Generative model G는 Generator 또는 생성자,
Discriminative model D는 Discriminator 또는 판별자라고 표기하도록 하겠습니다.
또한 GAN은 비전 뿐만 아니라 다양한 분야에 쓰이지만,
가짜 이미지 데이터를 생성하는 상황을 가정하여 글을 작성하도록 하겠습니다.

간단하게 서로의 역할을 정리하면
생성자는 noise로부터 가짜 데이터를 만들어서, 판별자를 잘 속이기 위해 훈련됩니다.
판별자는 생성자가 만든 가짜 데이터를 잘 구분해 낼 수 있도록 훈련됩니다.
이때, 판별자는 [진짜 이미지:1 ~ 가짜 이미지:0] 의 확률을 내며,
우리의 목표처럼 생성자가 가짜 이미지를 진짜 이미지처럼 잘 만들게 되면,
결국 판별자는 모든 입력 이미지에 대해 0.5의 확률을 보이게 됩니다.

논문에서는 생성자는 위조 지폐범, 판별자는 경찰로 예시를 들고 있습니다.
위조 지폐범과 경찰은 적대적이지만 각자의 실력 향상이 서로의 발전을 이끌어 내게 됩니다.

Objective function

다음은 GAN의 목적함수 입니다. 이 목적함수를 통해 생성자는 원본 데이터의 분포를 학습할 수 있습니다.

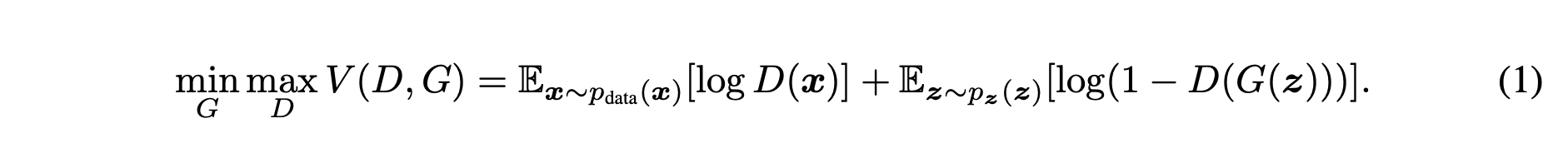
위 식을 자세히 분석 해보도록 하겠습니다.

하나의 식 $V(D,G)$에 대해,
$G$는 $V$의 값을 낮추는 방향으로,
$D$는 $V$의 값을 높이는 방향으로 노력하게 됩니다.

먼저 판별자 입장에서 오른쪽 두 항의 첫번째 항부터 보도록 하겠습니다.
여기서 $P_{data}(x)$는 원본 데이터의 분포를 의미합니다.
즉, 원본 데이터에서 $x$를 샘플링 한다는 의미입니다.
이 샘플링된 $x$를 $D$에 넣은 값에 $log$를 취해 평균을 구합니다.

두번째 항의 $P_z(z)$은 noise를 뽑아낼 수 있는 분포를 의미합니다.
(생성자는 기본적으로 noise vector로부터 입력을 받아 이미지를 만들어 냅니다)
이렇게 샘플링된 noise를 $G$에 넣어서 가짜 이미지를 만들어 낸 뒤,
이 가짜 이미지 $G(z)$를 $D$에 넣은 값을 1에서 빼서 $log$를 취해 평균을 구합니다.

이때 판별자 입장에서 $V(D,G)$ 가 최대가 되기 위해서는,
$D(x)$가 1이 되어야 하고,(진짜는 진짜로 구분)
$D(G(z))$가 0이 되어야 합니다.(가짜는 가짜로 구분)

반면 생성자는 두번째 항만 사용합니다.
이때 생성자 입장에서는 $D(G(z))$가 1이 되어야 판별자를 속인 것이므로,
두번째 항을 minimize 하는 방향으로 학습하게 됩니다.

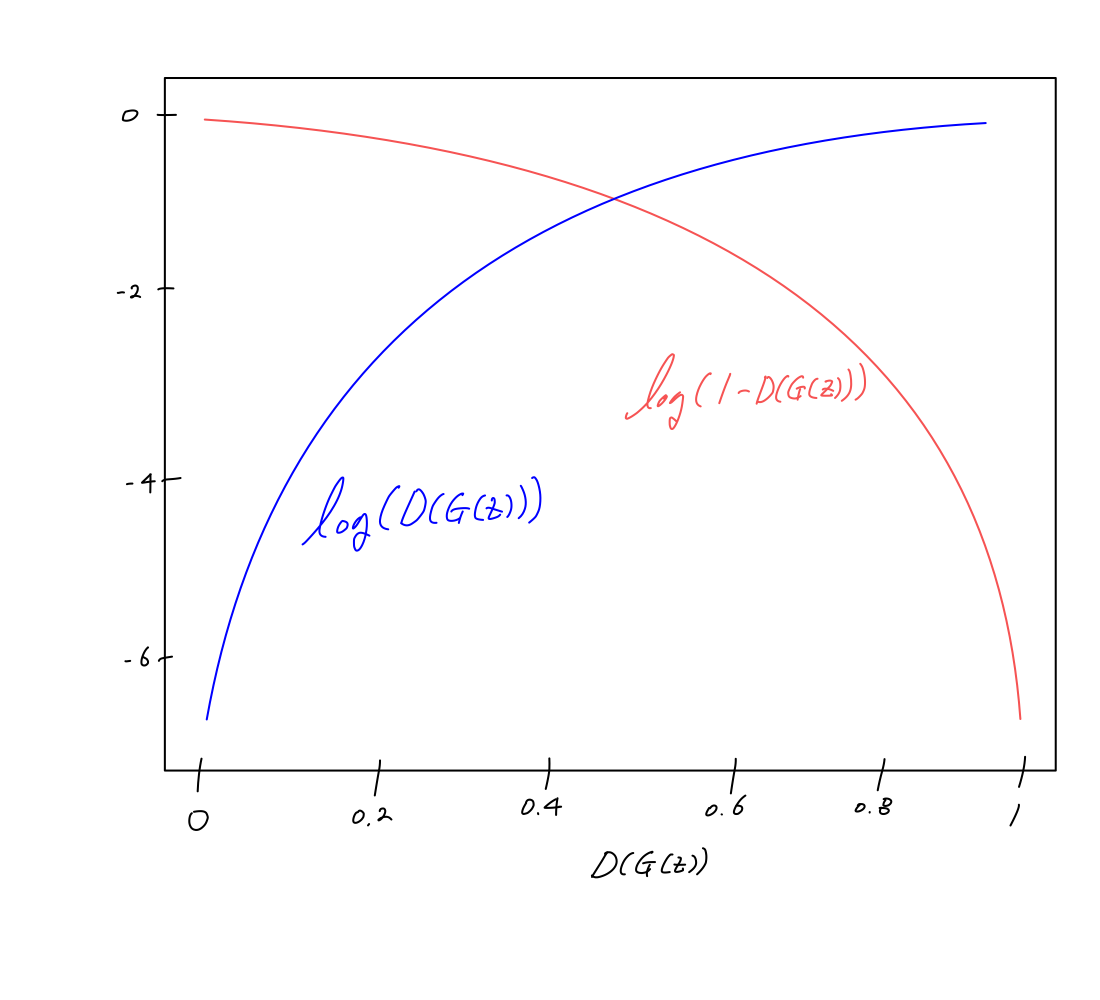
💡 실제 training에서는 $log(1-D(G(z)))$ … ① 를 minimize 하는 것 보다,
$logD(G(z))$ … ② 를 maximize 하는 방법으로 사용한다고 합니다.
그 이유는 아래와 같습니다.

위 그림에서 보면 $D(G(z))$ 가 0에 가까울 수록, 생성자의 성능이 좋지 않다고 볼 수 있습니다.
그렇다면 0에 가까울 때 학습이 필요한 상태인데,
① 식(빨간색 실선)은 gradient 크기가 작아서 천천히 학습됩니다.
하지만 ② 식(파란색 실선)은 gradient 크기가 커서 초반에 빠르게 학습될 수 있습니다.

Goal of GAN

위에서 본 그림을 다시 한번 보겠습니다.

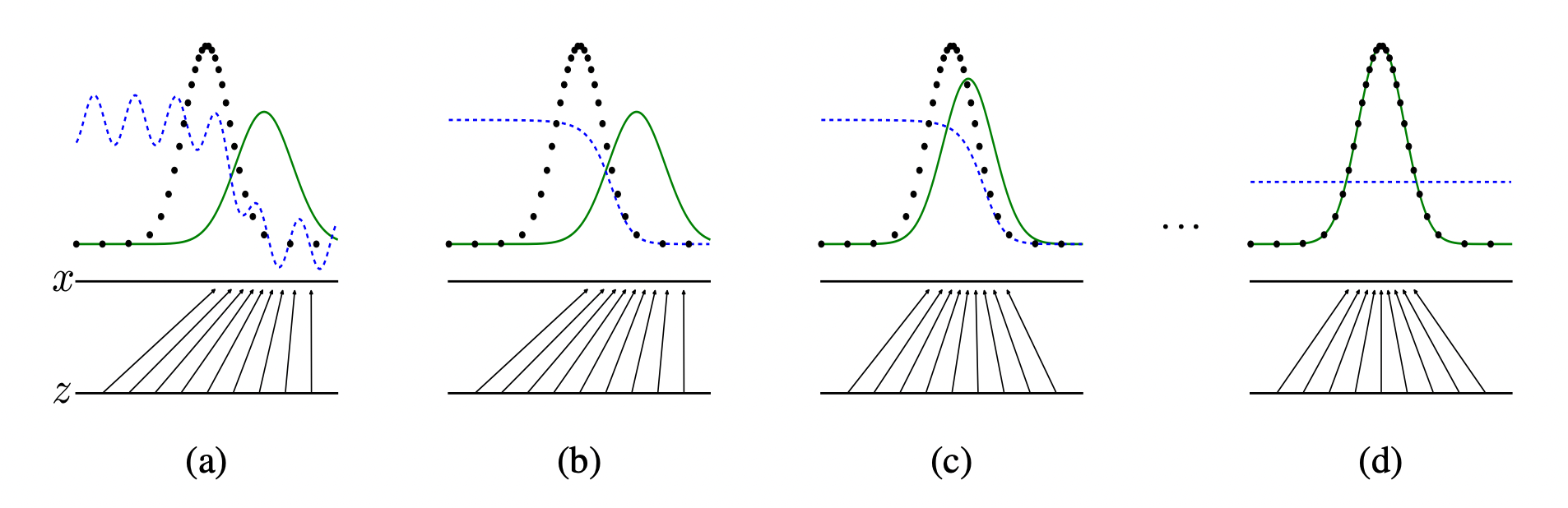
초반에는 판별자(파란색 점선)가 가짜 이미지를 잘 구분해냄을 볼 수 있습니다.
위의 목적 함수로 모델을 잘 학습 시켰다고 가정하면,
결국 생성자의 분포(초록색 실선)는 원본 데이터의 분포를 따르게 되고,
판별자는 가짜와 진짜 이미지를 구분할 수 없게 되어 1/2 로 수렴하게 됩니다.

여기서 생성자의 분포가 원본 데이터의 분포를 잘 따를 수 있도록,
즉 $Pg$가 $P_{data}$로 수렴할 수 있도록 하는게 GAN의 목표입니다.

Global Optimality of $p_g=p_{data}$

이 논문에서는 각 생성자 또는 판별자의 Global Optimality를 증명하기 위해,
어떠한 상황을 가정하고 생성자와 판별자가 각각 어떤 포인트에서 Global Optimality를 갖는지 설명합니다.

Proposition 1.

$G$가 고정 되었을때, $D$는 다음의 optimal point로 수렴합니다.

증명)

위의 식 (1) 로부터 다음의 식을 유도 할 수 있습니다.

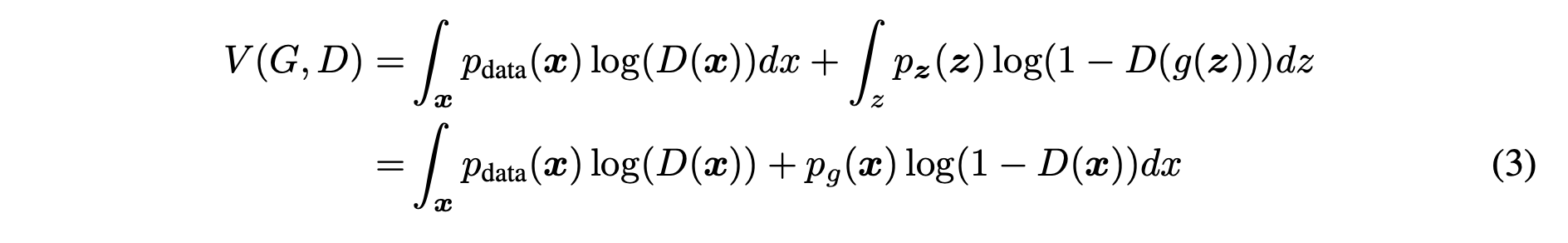
식 (3)-1 식은 식 (1)에서 각 확률에 대한 기댓값을 확률 밀도 함수의 적분으로 변환한 것입니다.
이때, $z$ 도메인에서 샘플링 된 noise벡터를 $g$에 넣어서 데이터 $x$를 만들어 낼 수 있고,
이는 도메인 $z$에서 $x$로 매핑되는 과정으로 볼 수 있습니다.
따라서 $x$로 치환하여 식 (3)-2로 변환할 수 있습니다.

이때 어떤 함수 $y$에 대해 다음의 모양 $a\thinspace log(y)+b\thinspace log(1-y)$ 을 가지는 경우, $a\over a+b$ 에서 최댓값을 갖는 것을 미분을 통해 쉽게 알 수 있습니다.
그리고 식 (3)-2는 바로 위의 식과 같은 형태임을 볼 수 있습니다. $(p_{data}\to a,\ \ p_g\to b)$
따라서 함수 $D$가 식 (2)와 같은 분포를 가질 때, 식 (3)의 적분식이 최댓값을 가진다고 할 수 있습니다.

Proposition 2.

Generator의 global optimum point는 $p_g=p_{data}$ 인 경우 입니다.

증명)

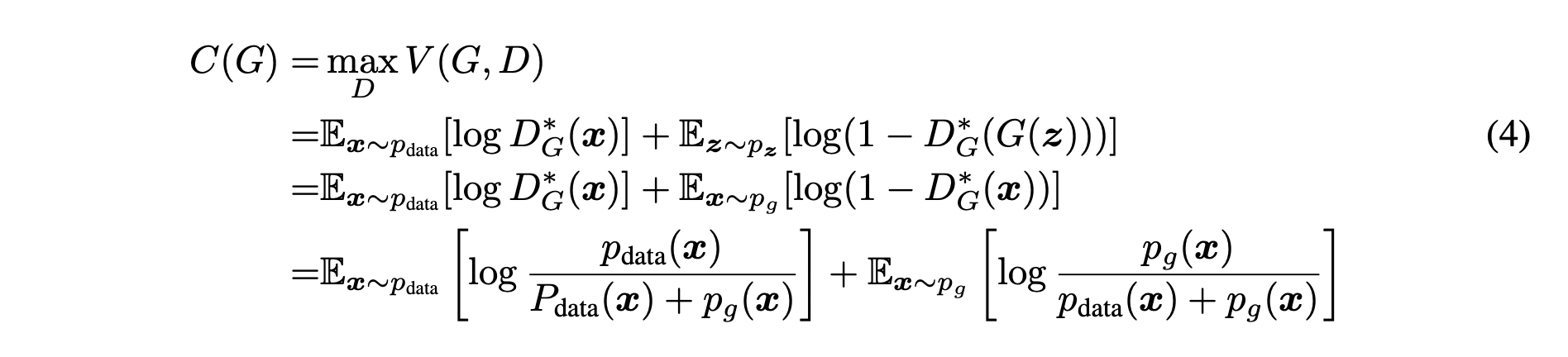
여기서는 식 (4)와 같이 새로운 함수 $C(G)$를 정의하겠습니다.
함수 $C(G)$는 $V$값을 최대로 만드는 $D$에 대한 $V$의 함수 입니다.
따라서 위에서 증명한 대로 $D$에 식 (2)를 대입하여 식 (4)-4를 만들 수 있습니다.

여기서 증명의 편의를 위해 식 (4)-4 의 $log$ 함수의 분자자리에 각각 2를 곱해주고,
전체 식에 $-log4$를 더해줍니다.
이는 $log$함수의 기본 성질이기 때문에 문제가 없습니다.

이렇게 바꾸면 두 $log$ 함수에 대한 부분은 KL divergence(KLD)로 아래 식과 같이 치환 될 수 있습니다.
(KLD 는 두 개의 분포가 있을 때, 이 두 분포가 얼마나 차이나는지에 대한 정보를 담고 있습니다)

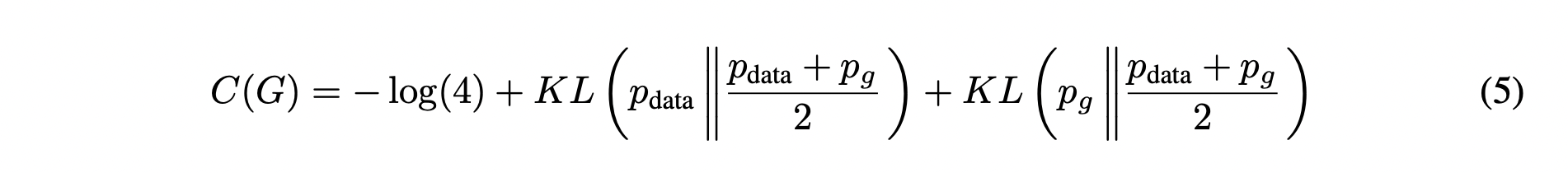
위와 같이 바꿔주게 되면, Jensen-Shannon divergence(JSD)를 이용하여 아래와 같이 표현할 수 있습니다.
(JSD 는 두개의 분포가 있을 때, 이 두 분포의 distance를 구하는 데에 사용할 수 있습니다)

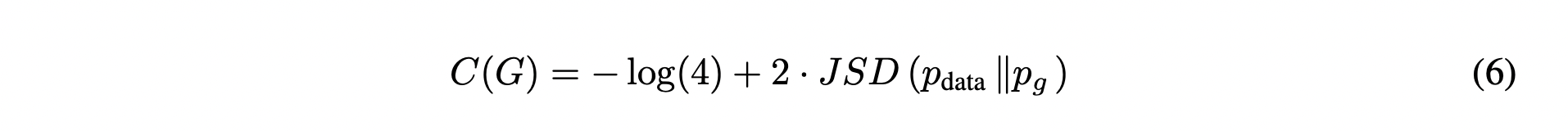
이때 JSD는 distance metric이기 때문에,
최솟값을 0으로 가집니다.
즉, 식 (6) 에서 $p_{data}, p_g$가 동일한 값을 가질 때, 뒤의 항은 0의 최솟값을 갖고,
따라서 $C(G)$의 최솟값은 $-log(4)$ 임을 볼 수 있습니다.

다시 정리하면, 이러한 global optimum point를 얻을 수 있는 유일한 경우는,
생성자가 만든 이미지와 원본 이미지의 분포가 동일할 때 입니다.

GAN Algorithm

전체적인 구조를 보면,
매 epoch당 판별자를 $k$번 학습 한 후에, 생성자를 학습하는 것을 볼 수 있습니다.
판별자를 학습 할 때에는 $m$개의 noise, $m$개의 원본 데이터를 샘플링하여 gradient ascent로 식의 값을 maximize 하는 방향으로 학습 하는 것을 볼 수 있습니다.
생성자를 학습 하는 경우, $m$개의 noise를 샘플링하여 $m$개의 가짜 이미지를 만들고, gradient descent로 위 식의 값을 minimize 하는 방향으로 학습 하는 것을 확인할 수 있습니다.

Result

위의 그림을 다시 보면, 단순히 training 데이터에 있는 이미지를 암기한 것이 아닌것을 확인할 수 있습니다.
(a)를 보면 가장 nearest한 데이터를 뽑았을 경우(5, 6열)에도, 선의 굵기나 필체가 다른것을 볼 수 있습니다.

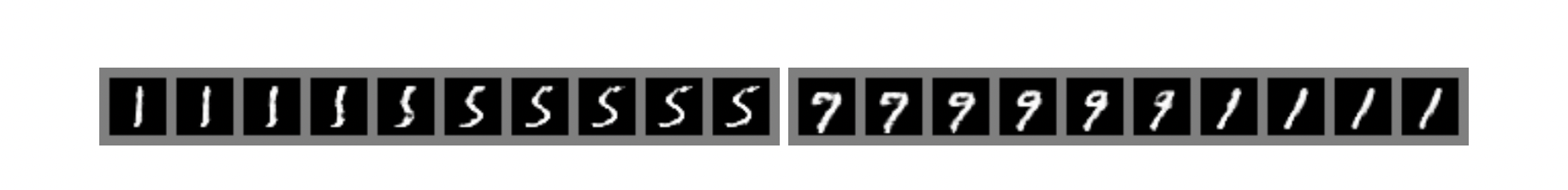
또한 위의 그림은 latant space상에서 1을 의미하는 벡터에서 5를 의미하는 벡터로(또는 7에서 1로) 선형으로 interpolation을 수행하여 이미지로 변환했을 때, 자연스럽게 변화하는 모습을 볼 수 있는 그림입니다.
즉, 이것 또한 이미지를 단순히 기억하고 있는것이 아니라 training 데이터를 바탕으로 그럴싸한 이미지를 만들어 낼 수 있는 능력을 갖고 있음을 보여줍니다.

참고: 동빈나 님의 유튜브