LDA (Linear Discriminant Analysis)

imgreen·2024년 9월 7일

개념정리/공부

목록 보기

2/4

LDA(Linear Discriminant Analysis)

PCA처럼 차원축소하는 방법 중 하나
다른점은 PCA보다 ‘분류’에 초점을 맞춘 것.
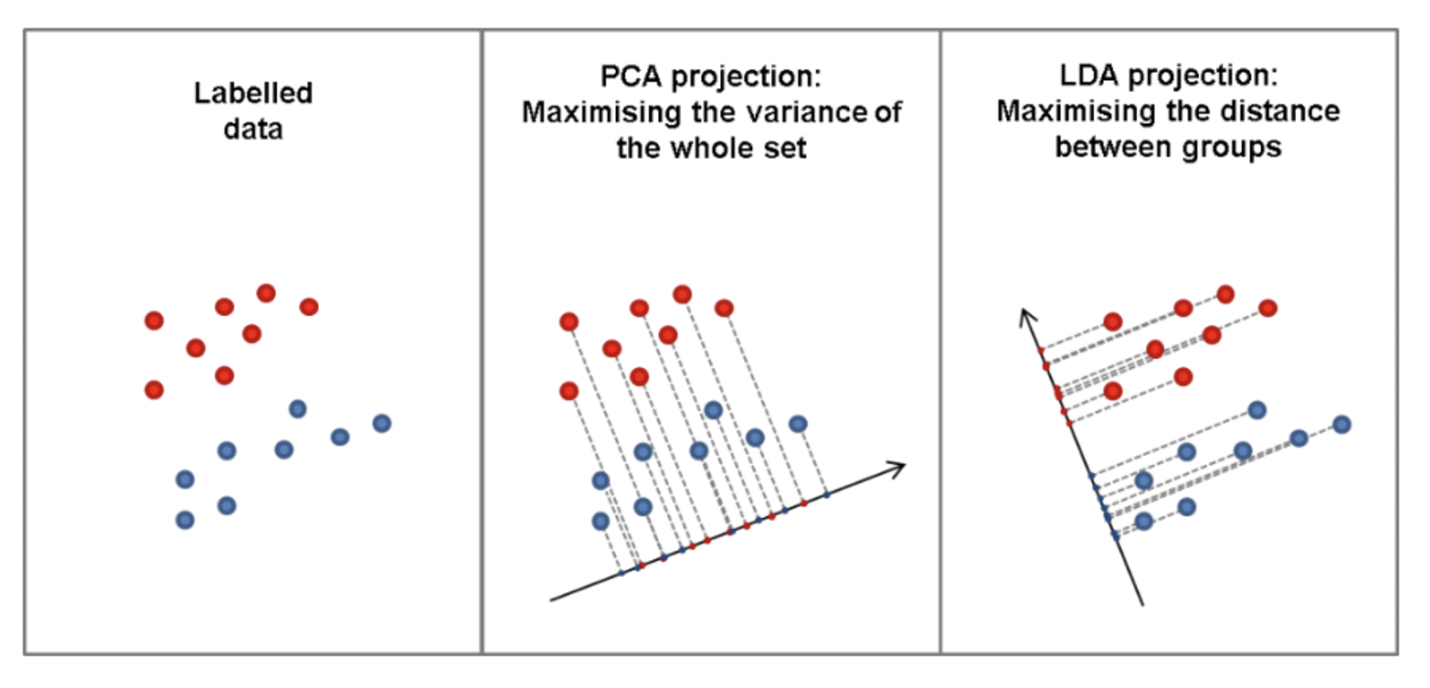
PCA가 전체 데이터의 분산을 가장 크게 만들어, 가장 많은 정보를 담고 있는 축을 찾는 것에 집중했다면 (차원 축소가 더 큰 비중)
LDA는 그룹 내의 분산을 오히려 작게 만들고, 그룹 간 분산은 크게 만든다! → 한 축으로 정사영 시켰을 때, (=한 차원으로 축소시켰을 때) 분류가 직관적으로 가능하게끔 만들어줌! (분류 목적이 더 큰 비중)

💡 그럼 저 분류할 수 있는 linear 식을 어떻게 찾느냐? 가 중요한 문제!

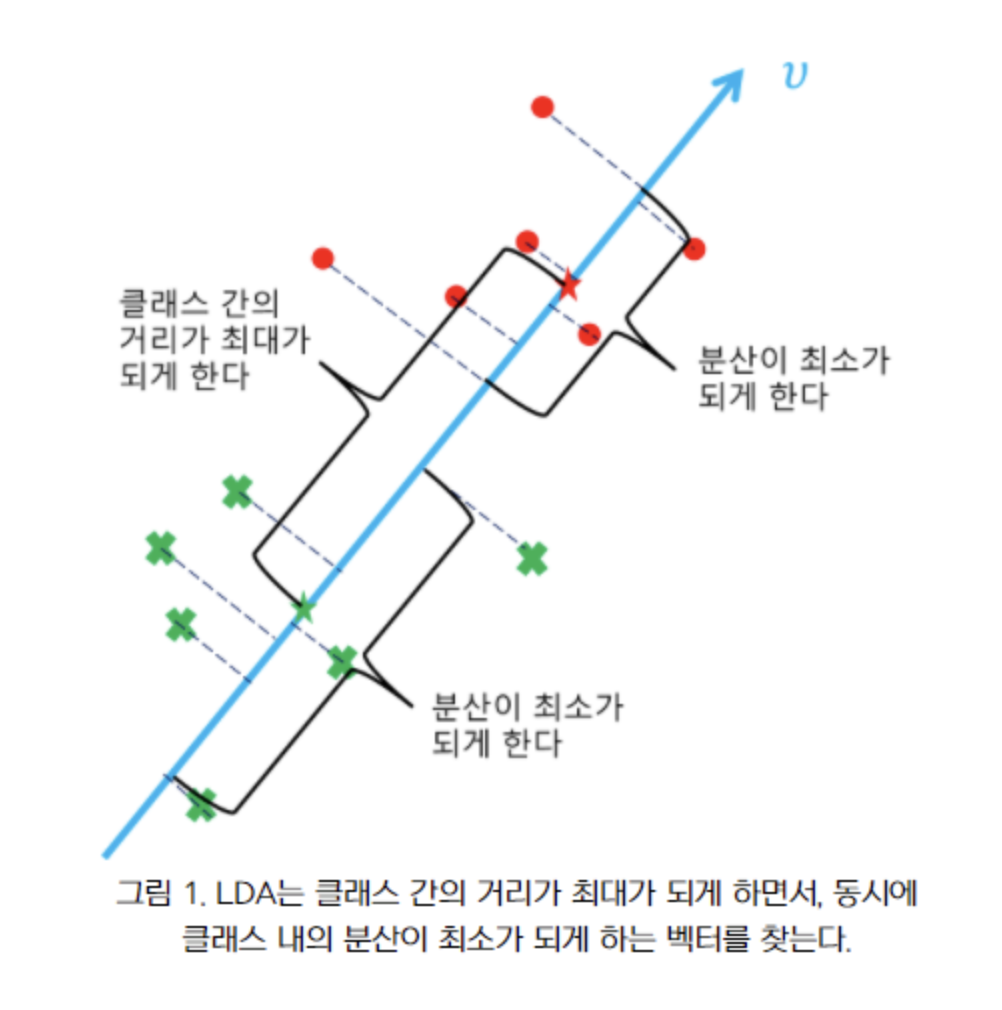
: LDA의 결정 경계

위 그림에서 정사영축(파란선)에 직교하는 축(점선)

⇒ 분류할 수 있는 linear 식

정사영한 두 분포가 만족해야 하는 것? : 정사영 축 찾기에 활용할 성질

각 클래스의 평균의 차이가 큰 지점을 결정 경계로 지정👉 빨간선 (μ1−μ2)이 길어야 함
각 클래스 내의 분산이 작은 지점을 결정 경계로 지정👉 검정선(δ2)이 짧아야 함

(출처: https://velog.io/@swan9405/LDA-Linear-Discriminant-Analysis)

<위 조건을 만족하는 수식 증명>

주요 노테이션

p: p차원의 입력벡터 (변수 p개) 인 data라고 생각
w: 정사영 시킬 축 (우리가 찾을 축)
y: 데이터 x를 w벡터에 사영 시킨 후 생성되는 값. (=변환값)
분류 값은 총 2개라고 가정 : C1,C2 두개의 클래스
각각 N1개, N2개 라고 가정

증명 과정

y = \vec{w}^T \vec{x}

m_1 = \frac{1}{N_1} \sum_{n \in C_1} x_n

m_2 = \frac{1}{N_2} \sum_{n \in C_2} x_n

클래스별 평균과 y 행렬 생성

y= \vec{w}^T\vec{x}

μ_1=\tfrac{1}{N_1} \sum_{\substack n\in C_1} x_n , μ_2=\tfrac{1}{N_2} \sum_{\substack n\in C_2} x_n

사영 후 평균 행렬: m_k 로 표시
사영 후 분산 행렬: s_k로 표시

💡 두 범주의 중심은 최대화하고, 분산은 최소화하는 게 우리의 목표

목적함수 J(w) 생성

→ S_B와 S_W는 각각 푼 값

( S_B는 클래스가 얼마나 떨어져 있는 지를 나타내는 집단 간 분산 between)

(S_W는 클래스 내에서 데이터가 얼마나 떨어져 있는 지를 나타내는 집단 내 분산 within)

우리읨 목적은 S_B가 크고 S_W가 작아야 함.

J(w) = \frac{(m_1 - m_2)^2}{s_1^2 + s_2^2} = \frac{w^T S_B w}{w^T S_W w}

S_B = (m_1 - m_2)(m_1 - m_2)^T

S_W = \sum_{n \in C_1} (x_n - m_1)(x_n - m_1)^T + \sum_{n \in C_2} (x_n - m_2)(x_n - m_2)^T

목적함수의 최댓값 찾기: 라그랑주 승수법+고윳값 분해 활용하기 $(w^T S_B w) S_W w = (w^T S_W w) S_B w$

S_W w = \lambda S_B w

S_B^{-1} S_W w = \lambda w

👉 결국, 우리는 람다로 둔 J(w) 값(람다로 둠) 이 가장 커지는 값을 찾기 위해 고윳값분해를 진행함! ⇒ 고윳값분해로 얻은 고윳값의 최댓값에 해당하는 고유벡터가 우리가 원하는 축, W벡터가 됨.

예측

→ 새로운 data x가 주어지면 이를 w와 내적하여 각각 클래스의 스코어를 구할 수 있음.

→ 스코어가 일정값(스스로 설정, 보통 0.5) 보다 크면 C1, 작으면 C2범주가 됨

코드

# 필요 라이브러리 import 

import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

# 기본 실습에 사용할 간단한 가상 데이터

X = np.array([[-1,-1], [-2,-1], [-3,-2], [1,1], [2,1], [3,2]])
y = np.array([1,1,1,2,2,2])

# 기본적인 LDA 구현

clf = LinearDiscriminantAnalysis()
clf.fit(X,y)

# 가상 데이터 클래스 예측

clf.predict([[-0.8,-1]])