Eigen-Decomposition, PCA, SVD

인화·2025년 10월 19일

Eigen-Decomposition PCA SVD machine learning 기계학습

기계학습

목록 보기

3/3

벡터와 행렬

벡터와 행렬의 개념

벡터 : 방향과 크기를 갖는 대상
행렬 : 여러 벡터를 열로 담은 구조
- 행렬은 교환법칙이 성립하지 않는다. ( $AB ≠ BA$ )
- 행렬은 분배법칙과 결합법칙이 성립한다.
- $A(B + C) = AB + AC$ (분배법칙), $A(BC) = (AB)C$ (결합법칙)
- 행렬의 곱셈을 위해선 행렬 A의 열과 행렬 B의 행의 개수가 같아야 한다.
텐서 : 3차원 이상의 구조를 갖는 배열
설계 행렬 (Design Matrix) : 학습 데이터를 담은 행렬 (n samples * d features)
전치 $A^T$ , 역행렬 $A^{-1}$ , 단위 행렬 $I$
행렬식 $det(A)$ : 선형 변환의 부피 스케일링 (부호는 방향성)
특수한 행렬들

역행렬 (Inverse Matrix)

행렬 A와 곱하면 단위 행렬 I가 나오는 행렬 $A^{-1}$ 를 역행렬이라고 하며, 이는 정방행렬(행과 열의 수가 같은 행렬)에 대해서만 정의되고, 역행렬이 없으면 특이행렬(Singular Matrix)이라고 한다.

\mathbf{A} = \begin{bmatrix}a & b \\c & d\end{bmatrix}, \quad\mathbf{A}^{-1} = \frac{1}{ad - bc}\begin{bmatrix}d & -b \\-c & a\end{bmatrix}

역행렬은 곱했을 때 항등 행렬을 만들어 내는 성질을 지닌다.

AA^{-1} = A^{-1}A = I

A = np.array([[1., 2., 3.,],
             [3., 4., 5.],
             [7., 8., 10.]])

print("A = \n", A) # 기본 행렬 출력
print("A^T = \n", A.T) # 전치된 행렬 출력
print("det(A) = ", npl.det(A)) # 행렬식 계산
print("A inverse (via scipy) : \n", sl.inv(A)) # 역행렬 계산
# 역행렬은 곱했을 때 항등행렬을 만들어 내는 성질을 지님. (AA^{-1} = A^{-1}A = I)
print("A * A^{-1} = l : \n", A @ sl.inv(A))

전치행렬 (Transpose Matrix)

전치행렬이란, 행렬의 행과 열을 교환한 행렬을 의미한다.

\mathbf{A} =\begin{bmatrix}1 & 2 & 3 \\4 & 5 & 6 \\7 & 8 & 9\end{bmatrix}\Rightarrow\mathbf{A}^{\mathrm{T}} =\begin{bmatrix}1 & 4 & 7 \\2 & 5 & 8 \\3 & 6 & 9\end{bmatrix}

\mathbf{B} =\begin{bmatrix}x & y \\z & w\end{bmatrix}\Rightarrow\mathbf{B}^{\mathrm{T}} =\begin{bmatrix}x & z \\y & w\end{bmatrix}

\mathbf{C} =\begin{bmatrix}1 & 1 & 1 & 1 \\-3 & 5 & -2 & 7\end{bmatrix}\Rightarrow\mathbf{C}^{\mathrm{T}} =\begin{bmatrix}1 & -3 \\1 & 5 \\1 & -2 \\1 & 7\end{bmatrix}

행렬식(Determinant)과 행렬식의 기하학

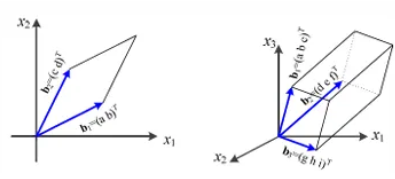
행렬식이란, 행렬 공간을 얼마나 늘이거나 줄이는지, 선형 변환의 부피 스케일링을 의미하는 값이다. 다시 말해, 선형 변환의 부피 변화율을 나타내는 값이다.

A =\begin{bmatrix}a & b \\c & d\end{bmatrix}

\text{det}(A) = ad - bc

행렬식은 어떤 행렬의 역행렬 존재 여부에 대한 판별값이 되기도 하며, 행렬식의 값이 0이면 역행렬이 존재하지 않는다. 행렬식은 정방 행렬에 대해서만 정의되며, 기하학적으로는 2차원에서는 2개의 행 백터가 이루는 평행사변형의 넓이를, 3차원에서는 3개의 행 벡터가 이루는 평행 사각 기둥의 부피를 의미한다.

예시 코드

$A = [a_1, a_2]$ (열벡터 $a_1, a_2$ ) 일 때, $|det(A)|$ 는 $a_1, a_2$ 가 만드는 평행사변형의 면적이다.

# 선형 변환 결과 확인하는 코드
# 행렬식 det(A)가 선형 변환의 부피 스케일링 의미하는 거니까
# 결국엔 det(A)만큼 선형변환 적용한 결과를 시각화한 그래프 !
# 그래프 Before, After 보면 각 단위 면적이 3배 커진 걸 확인 가능함.
A2 = np.array([[2., 1.,],
               [1., 2.,]])

print("det(A2) =", npl.det(A2)) # A2 행렬식 계산

# 격자와 변환된 격자 시각화
# (11, 11, 2) -> (121, 2)
# np.stack() -> 새로운 차원(축) 추가해 배열 합침
# np.meshgrid() -> 2차원 평면 위에 격자의 좌표망 만듦
grid = np.stack(np.meshgrid(np.linspace(-1, 1, 11), np.linspace(-1, 1, 11)), axis=-1).reshape(-1, 2)
grid_T = grid @ A2.T # 모든 격자점에 선형 변환 적용 (행렬곱)

plt.figure(figsize=(5,5))
plt.scatter(grid[:,0], grid[:,1], s=10) # 원래 점 표시 / s = 점 크기
plt.scatter(grid_T[:,0], grid_T[:,1], s=10, marker='x') # 선형 변환 적용된 점 표시
plt.axis('equal'); plt.title("Before (•) / After (x) by A2") # plt.axis('equal'); x, y축 스케일 맞춤
plt.show()

고유값/고유벡터

고유값/고유벡터 : 정의와 직관

$n*n$ 정방 행렬 A에 대해 $Av = \lambda v$ 를 만족하는 $v ≠ 0$ 를 A의 고유 벡터, $\lambda$ 를 고유값이라고 한다. 다시 말해, 고유 벡터는 행렬 A를 선형 변환했을 때, 선형 변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터를 의미하고, 고유값은 그 상수배 값(고유벡터의 변화되는 스케일 정도)를 의미한다. 이때, A의 고유 벡터는 A에 선형 변환을 취해도 방향이 변하지 않고, 크기만 변한다.

대칭행렬은 $A = A^T$ 이므로 항상 실수 고유값을 지니고, 고유벡터를 만드는 행렬 A가 대칭행렬일 때 서로 다른 고유값을 가지는 고유벡터는 서로 직교한다. (모든 대칭행렬의 고유벡터는 서로 직교(orthogonal)한다)

여기서 직교는 고유벡터의 값이 서로 수직이어서 두 벡터의 내적 결과가 0이 나온다는 것을 의미한다.

키워드 : 불변 방향, 크기 스케일링, 대칭행렬, 직교
고유값 : $det(A - \lambda I) = 0$ . $\begin{vmatrix}a - \lambda & b \\c & d - \lambda\end{vmatrix}= \lambda^2 - (a + d)\lambda + (ad - bc) = 0$
고유벡터 : $(A - \lambda I) V = 0$

예시 코드 - 고유값 분해와 Av = λv 검증

A = np.array([[4., 2.],
              [3., 5.]])
vals, vecs = npl.eig(A) # 고유값 분해
print("A = \n", A) # A 행렬 출력
print("eigenvalues =", vals) # A의 고유값
print("eigenvectors (columns) = \n", vecs) # A의 고유벡터

# 검증 Av = λv
for i in range(len(vals)):
  v = vecs[:, i] # i번째 고유 벡터
  Iv = vals[i] * v # i번째 고유값 * 고유벡터 (λv)
  Av = A @ v # Av 계산
  # Av - λv = 0이 성립하면 Av = λv인 것.
  print(f"i = {i} : ||Av - λv|| = " , npl.norm(Av - Iv))

예시 코드 - 2D 변환에서의 시각적 의미

임의의 A가 평면 전체의 방향을 뒤섞어도 고유 벡터의 방향은 그대로 남는다.

A = np.array([[2.,1.],
              [0.5,1.5]])

vals, vecs = npl.eig(A) # 고유값 고유벡터 계산
# (289, 2)
grid = np.stack(np.meshgrid(np.linspace(-2,2,17), np.linspace(-2,2,17)), axis=-1).reshape(-1, 2)
grid_T = grid @ A.T # 모든 격자점에 선형 변환 적용 (행렬곱)

plt.figure(figsize=(5,5))
plt.scatter(grid[:,0], grid[:,1], s=8)
plt.scatter(grid_T[:,0], grid_T[:,1], s=8, marker='x')
for i in range(2):
  v = vecs[:,i].real # i번째 고유벡터 실수부 (대칭행렬이 아니라 고유벡터가 복소수일 수 있어서)
  # 벡터 크기를 1로 정규화
  v = v/npl.norm(v) # np.linalg.norm(v) : 벡터 v의 길이 계산
  t = np.linspace(-2,2,100)[:,None] # -2 ~ 2까지 100개 점 만들고, (100, 1) 형태로 만듦
  line = t*v[None,:] # (100, 1) (1, 2) -> (100, 2) / 고유벡터 방향으로 -2~2배까지 점 찍음
  plt.plot(line[:,0], line[:,1])
plt.axis('equal'); plt.title("Eigen-directions are invariant (lines)")
plt.show()

고유 벡터의 직교

대칭 행렬의 고유 벡터 집합은 서로 직교하나, 비대칭 행렬에서는 일반적으로 고유벡터가 직교하지 않는다.

고유벡터들이 직교하면 $Q^TQ = I$ 가 성립한다.

import numpy as np
import numpy.linalg as npl

# (1) 대칭행렬 : 고유벡터 직교성 확인
S = np.array([[2., -1., 0.],
              [-1., 2., -1.],
              [0., -1., 2.]])

valsS, vecsS = npl.eigh(S) # 대칭전용 -> 실수 / 직교 보장 (QR) / 다시 말해, npl.eigh(S)는 고유값과 고유벡터가 실수이고 고유벡터들이 직교하도록 보장함
# 고유벡터들이 직교하면 Q^TQ = I가 성립함.
print("Symmetric eigenvectors orthogonality (Q^T Q ≈ I) : \n", vecsS.T @ vecsS)

# (2) 비대칭행렬 : 일반적으로 직교 아님 (Q^T Q ≠ I)
# -> 다르게 표현하면 Off-diagonal 값이 0이 아님 (직교하지 않음)
B = np.array([[1., 2.],
              [0., 3.]])

valsB, vecsB = npl.eig(B)
print("Nonsymmetric eigenvectors dot products : \n", vecsB.T @ vecsB)

파워 반복(Power Iteration)과 Rayleigh Quotient

Power Iteration이란, 행렬의 가장 큰 고유값과 그에 대응하는 고유벡터를 근사적으로 찾는 알고리즘이다. (행렬을 계속 곱하다 보면 가장 큰 고유값과 고유벡터만 살아남는다는 것)

고유값이 크다 = 정보량이 많다(해당 방향이 데이터의 분산이 크다)는 의미이며, PCA에서는 고유값이 큰 고유벡터만 남기고 지우는 방식으로 차원 축소한다. 따라서 고유값이 큰 순서대로 몇 개의 고유벡터만 남기고 작은 건 버려야 하는데, 고유값이 큰 걸 찾을 수 있는 알고리즘 중 하나가 Power Iteration이다.

Rayleigh Quotient이란, 벡터 x를 A로 변환했을 때 방향/크기의 비율을 측정하는 것이다. 따라서 x가 고유벡터라면, Rayleigh Quotient를 통해 고유값을 계산할 수 있다.

x_{k+1} \leftarrow \frac{A x_k}{\| A x_k \|} \quad \text{→ 지배적 고유벡터로 수렴.}

R(x) = \frac{x^{\mathrm{T}} A x}{x^{\mathrm{T}} x}\quad \text{→ } x가 \text{ 고유벡터일 때 } R(x) = \lambda.

def power_iteration(A, num_iter=30):
  x = rng.normal(size=(A.shape[0], )) # 행렬 A 크기에 맞춰 초기 벡터 난수 생성
  x = x / npl.norm(x) # 정규화
  history = [] # Rayleigh quotient 기록하는 리스트
  # 행렬(A)을 계속 곱하다 보면 가장 큰 고유값과 고유벡터만 살아남는다 -> power_iteration
  # Av = λv이므로 계속 곱하면 그 벡터의 방향은 변하지 않고 크기만 고유값만큼 커지므로
  # 계속 곱하면 가장 큰 고유값을 가진 방향으로 수렴함.
  for _ in range(num_iter):
    x = A @ x # Ax
    x = x / npl.norm(x)
    r = (x @ (A @ x)) / (x @ x) # Rayleigh quotient 계산
    history.append(r)
  return x, np.array(history) # 가장 큰 고유값에 대응하는 고유벡터로 추정된 벡터 return

A = np.array([[4., 2., 0.],
              [2., 3., 1.],
              [0., 1., 2.]])

x_star, rq_hist = power_iteration(A, num_iter=25) # Power Iteration 실행
vals, vecs = npl.eigh(A) # 고유값, 고유벡터 구하기
idx = np.argmax(vals) # 가장 큰 고유값 인덱스 추출
print("Power-iter dominant eigenvalue (approx) = ", rq_hist[-1]) # 마지막 반복에서의 Rayleigh Quotient (행렬 A의 가장 큰 고유값)
print("True dominant eigenvalue = ", vals[idx])

plt.figure()
plt.plot(rq_hist)
plt.xlabel("iteration"); plt.ylabel("Rayleigh quotient")
plt.title("Convergence of Rayleigh quotient to dominant λ")
plt.show()

고유값 분해 (Eigen-Decomposition)

고유값 분해 (Eigen-Decomposition)란, 행렬을 고유값과 고유벡터를 통해 분해하는 기법으로, 어떤 정방행렬 A를 $A = QΛQ^{-1}$ 의 형태로 쪼개는 것을 의미한다. 이때, Q는 A의 고유벡터를 열에 배치한 행렬, Λ는 고유값을 대각선에 배치한 대각행렬을 의미한다.

이렇게 고유값 분해를 수행하면 행렬을 그 행렬만의 좌표계(고유 벡터)로 바꾸어 단순 대각 형태로 만들어 주며, 이는 PCA에서 주로 활용된다. 고유값이 크다는 것은 그 방향에 데이의 정보량이 많다는 의미이기에 정보량이 큰 데이터만 남기고 차원을 축소할 수 있기 때문이다.

대각화 가능하다 = 행렬 A를 고유벡터와 고유값으로 분해할 수 있다
다시 말해, 고유값 분해가 가능하고, $A = QΛQ^{-1}$ 의 형태로 표현이 가능하다는 것을 의미함.

고유값 분해를 해주면, 대각행렬 Λ가 단순 스케일 행렬임을 볼 수 있다. (이는 표준 기저에서 봤을 땐 복잡한 변환이었는데, 좌표계를 고유벡터 기준으로 바꿨더니 A가 단순히 각 좌표 성분을 $\lambda_i$ 배 해주는 행렬로 보이더라! 라는 느낌으로 이해하면 된다.)

Q의 열벡터들을 고유벡터로 구성한 이유는 결국엔 이 벡터들이 만드는 좌표계가 고유기저이기 때문이고, 결국 고유값 분해는 이 고유 기저를 기준으로 행렬을 분해하는 것을 의미한다고 볼 수 있다.

# 일반 행렬의 고유값 분해
A = np.array([[4.,2.],
              [3.,5.]])

vals, vecs = npl.eig(A) # 고유값과 고유벡터 계산
V = vecs
L = np.diag(vals) # 대각행렬 만드는 함수
A_rec = V @ L @ npl.inv(V) # A = VΛV^{-1}
print("||A - VΛV^{-1}||", npl.norm(A - A_rec)) # A와 고유값 분해된 값 비교

# 대칭 행렬의 고유값 분해
# 대칭 (스펙트럴 정리(Spectral Theorem) - 대칭행렬은 항상 직교대각화 가능하다는 것) 확인
S = np.array([[2.,-1.],
              [-1.,3.]])
valsS, QS = npl.eigh(S) # 대칭전용 -> 실수 / 직교 보장 (QR)
# 직교행렬이면 역행렬이 전치행렬
# QQ^{T} = Q^{T}Q = I이고, QQ^{-1} = I이므로 Q^{-1} = Q^T
S_rec = QS @ np.diag(valsS) @ QS.T # A = QΛQ^{-1} = QΛQ^{T}
print("||S - QΛQ^T|| =", npl.norm(S - S_rec)) # S와 고유값 분해된 값 비교

PCA : 공분산의 고유 분해

PCA의 절차 (Code Example)

데이터의 평균을 0으로 정규화
공분산행렬 계산 - 공분산행렬은 대칭행렬이기에 항상 고유값 분해가 가능하다. 또한, 공분산은 데이터의 분산 구조를 담는 행렬이기에 공분산 행렬의 고유 벡터는 데이터의 분산이 최대/최소인 방향을 나타낸다. 이를 주성분 벡터라 부를 수 있고, 고유값은 그 방향에서의 분산 크기(정보량)를 의미한다.
고유값 분해
주성분 선택
차원 축소 및 원래 데이터 X를 선택된 주성분 벡터 W에 투영 (Z=XW)

from sklearn.datasets import load_digits

digits = load_digits()
X = digits.data.astype(float)
X = X - X.mean(axis = 0, keepdims=True) # 정규화
n = X.shape[0] # 데이터 샘플 개수
C = (X.T @ X) / n # 공분산행렬

vals, vecs = npl.eigh(C) # 대칭전용 -> 실수 / 직교 보장 (QR)
idx = np.argsort(vals)[::-1] # 고유값 내림차순 정렬 후, 가장 큰 고유값이 첫 번째가 되도록 순서 바꿈
vals, vecs = vals[idx], vecs[:, idx] # 고유벡터도 같은 순서 정렬

explained = vals / vals.sum() # 고유값이 전체 분산에서 차지하는 비율
print("Top-10 explained variance ratio : \n", explained[:10])

def pca_project(X, vecs, k):
  W = vecs[:, :k] # 앞에서부터 k개 주성분 벡터 선택 (64*k)
  Z = X @ W # Z = XW (원래 데이터 X를 선택된 주성분 벡터 W에 투영)
  return Z, W

def pca_reconstruct(Z, W):
  return Z @ W.T # ZW^T (축소된 데이터 Z를 원래 차원으로 복원)

# k = 주성분 개수
for k in [5, 10, 20, 40]:
  Z, W = pca_project(X, vecs, k)
  # digits.data.mean(axis=0, keepdims=True) - 원래 X에서 평균을 뺐었으므로 다시 더해줘서 복원
  Xk = pca_reconstruct(Z, W) + digits.data.mean(axis=0, keepdims=True)
  fig = plt.figure(figsize=(6, 2))
  for i in range(8):
    ax = plt.subplot(1, 8, i+1)
    ax.imshow(Xk[i].reshape(8,8), interpolation="nearest")
    ax.set_xticks([]); ax.set_yticks([])
  plt.suptitle(f"PCA reconstruction with k = {k}")
  plt.tight_layout()
  plt.show()

특이값 분해 (Singular Value Decomposition)

고유값 분해는 정방 행렬만 분해 가능하다. 따라서 정방 행렬이 아닌 경우(비정방행렬)에 대해서도 분해를 수행하기 위해선 특이값 분해를 활용해야 한다. 이는 임의의 행렬을 $A=UΣV^T$ 의 형태로 행렬을 쪼개는 것을 의미한다.

이때, 고유값은 행렬 A가 직사각행렬이면 입출력 차원이 달라 상수배(고유값)을 직접 정의할 수 없다. 따라서 길이(스케일 크기)만 추출하기 위해 $AA^T$ , $A^TA$ 의 결과가 항상 정방 행렬이고 대칭행렬인 점을 활용한다.

$U$ (왼쪽 특이행렬) : $AA^T$ 의 고유 벡터를 열에 배치한 n*n 행렬
$S$ (특이값 리스트) : $AA^T$ 의 고유값의 제곱근을 대각선에 배치한 대각 행렬 (n*m 행렬)
$V^T$ (특이행렬) : $A^TA$ 의 고유 벡터를 열에 배치한 m*m 행렬 $C = \frac{1}{n} X^T X = V \left( \frac{\Sigma^2}{n} \right) V^T \;\Rightarrow\; \text{PCA 고유벡터} = V, \quad \text{고유값} = \frac{\Sigma^2}{n}$

실제 차원 축소(PCA)의 구현에는 비정방행렬에도 적용이 가능한 보다 일반적인 방법인 SVD가 주로 사용된다.

# SVD로 얻은 주성분 벡터랑 공분산 고유분해로 얻은 주성분 벡터가 같은지 검증하는 코드

# PCA의 목표는 데이터가 가장 많이 퍼져있는 방향을 찾는 거
# 공분산 이용하는 이유 -> 데이터의 분산 구조를 담는 행렬이기 때문
# 따라서 공분산 행렬의 고유벡터 = 데이터 분산이 최대/최소인 방향
# = 주성분 벡터
# 고유값 = 그 방향에서의 분산 크기

# SVD로 얻은 V와 공분산 고유벡터 비교
from sklearn.datasets import load_digits
digits = load_digits()
Xraw = digits.data.astype(float)
Xc = Xraw - Xraw.mean(axis=0, keepdims=True)

# 행렬 Xc에 대해 SVD 분해
# U : 왼쪽 특이행렬 / S : 특이값 리스트 / VT : 오른쪽 특이행렬
U, S, VT = npl.svd(Xc, full_matrices=False)
V = VT.T
C = (Xc.T @ Xc) / Xc.shape[0] # 공분산
valsC, vecsC = npl.eigh(C) # 고유값, 고유벡터
idx = np.argsort(valsC)[::-1] # 가장 큰 고유값
vecsC = vecsC[:, idx] # 가장 큰 고유값에 대응하는 고유벡터

# 주성분 부호/순서 불확정성을 감안해 상관을 비교
# V = SVD에서 나온 오른쪽 특이벡터들 -> 공분산 행렬의 고유벡터와 같아야 함.
# C = 공분산행렬을 직접 고유분해해서 얻은 고유벡터
# V, C는 둘 다 직교행렬이므로 두 직교행렬을 곱하면 직교 행렬이 되며,
# 두 값이 완전히 같으면 곱한 값이 단위행렬이 됨.
# 따라서 SVD의 V와 공분산 고유벡터가 같은지 확인
# SVD 결과 = PCA임을 증명 가능함. (오른쪽 특이벡터랑 공분산 행렬이 같아야 PCA 결과 = SVD 결과가 성립)
corr = np.abs(np.diag(V.T @ vecsC))
print("Diagonal of |V^T * eigenvector(C)| (shold be near 1) : \n", corr[:10])

인화

얼렁뚱땅 바보 학부생...

이전 포스트