GoogLeNet

GoogLeNet

• 네트워크 내부의 컴퓨팅 자원 활용을 크게 개선한 모델
• 성능 최적화를 위해 Hebbian principle와 multi-scale processing(여러 크기 필터 동시 적용)을 적용함.
• 이 당시까지의 최신 트렌드는, 레이어 수를 늘리고, 레이어 크기를 키우는 방향으로 발전했고, 이 과정에서 과적합 해결을 위해 드롭아웃도 많이 사용함.
• Inception 모델은 모든 필터가 학습되며, Inception 레이어가 여러 번 반복되며, 22층 깊이의 네트워크가 됨.

Motivation and High Level Considerations

 DNN 성능 향상의 가장 직관적인 방법은 레이어 수와 레이어 당 유닛 수를 늘리는 것인데, 이는 네트워크 크기가 커질수록 파라미터 수가 급격히 증가하고, 네트워크 크기가 균일하게 증가할 경우 연산량이 급격히 늘어난다는 단점이 존재함.
- 완전 연결 대신 희소 연결 구조를 사용하면, 근본적 해결 가능하고, 이는 Hebbian 이론과도 일맥상통하나, 현재의 컴퓨팅 인프라에선 비효율적이며, CPU, GPU 등도 밀집 행렬에 최적화되어서 연산량이 많더라도 밀집 행렬 곱셈이 희소 행렬 곱셈보다 빠를 수 있음.
- 공간적 도메인에서 희소성을 어느 정도 활용 중임 (ex) 컨볼루션
- 현재 하드웨어의 밀집 행렬 연산 이점을 살리면서도 필터 수준에서의 희소성을 일부 활용할 수 있는 중간 단계의 아키텍처가 가능한가? ⇒ 희소 행렬을 상대적으로 밀집한 submatrix로 클러스터링하면 우수한 성능을 얻을 수 있음.
- 이러한 아이디어를 기반으로 시작해 희소 구조를 실제로 구현하되, 밀집된 기존 컴포넌트로 이를 대체한 것이 Inception 아키텍처이며(즉, 희소 연결처럼 작동하는 컨볼루션 블록들을 dense하게 만듦(여러 개 컨볼루션 결과를 합치는 형태)), 이는 local optimality를 지님.

** Contrast Normalization : 이미지 밝기/대비 균일하게 맞추는 것

Architectural Details

 Inception의 주요 아이디어는 컨볼루션 비전 네트워크에서 최적의 local sparse structure를 어떻게 쉽게 이용 가능한 dense 컴포넌트로 근사하고 덮을 수 있을까를 찾는 데 있으며, 이는 translation invariance를 가정하기에 컨볼루션 블록들로 구성되므로 최적의 국소 구조를 찾아내 이를 공간적으로 반복해야 함.

• 레이어별로 네트워크를 구축해 활성화 값 분석 → 비슷한 유닛끼리 묶고, 필터 뱅크를 통해 특징 추출 → 다음 레이어 구성
• 입력에 가까운 초기 레이어는 상관관계가 높은 유닛들이 대체로 이미지의 국소적인 영역을 보므로 1*1 컨볼루션으로 처리해도 충분하나(상관 있는 유닛들이 좁은 영역에 몰려있으므로), 어떤 유닛들은 더 넓은 영역에 걸쳐 활성화가 비슷할 수 있으므로 더 큰 필터가 필요함.
• 패치 정렬 문제(패치 기반 처리 방식에서 패치들이 서로 잘 안 맞는 문제)를 피하기 위해 11, 33, 5*5 필터 크기만을 사용하며, 서로 다른 크기 필터 레이어들을 조합해 각 레이어의 출력 필터 뱅크를 하나의 출력 벡터로 concatenate해 다음 단계의 입력으로 삼음. + 각 단계마다 병렬로 풀링 경로도 추가함.
  • 이러한 Inception 모듈을 층층히 쌓으면 출력 활성화 간 상관 통계는 변하고, 높은 레이어로 갈수록 더 높은 수준의 추상적 특징을 포착함.
• 하지만, 이러한 구조는 5*5 컨볼루션의 연산량이 매우 비싸고, 풀링 계층 추가 시 출력 필터 수가 이전 레이어와 같아 단계가 진행될수록 출력 수가 폭발적으로 증가한다는 단점이 존재함.
  • 이러한 문제 해결을 위해 적절한 지점마다 차원 축소와 projection을 적용함.
  • 저차원 임베딩이라도 비교적 큰 이미지 패치의 많은 정보를 담을 수 있으나, 임베딩은 정보를 압축된 형태로 표현하기 때문에, 모델링이 더 어려워진다는 단점이 있어, 희소 표현을 유지하되, 다수 신호를 한꺼번에 집계해야할 때만 압축하는 것이 목표임
  • 11 컨볼루션을 통해 차원 축소 수행 후, 비용이 많이 드는 33, 5*5 컨볼루션을 적용함.
  • 1*1 컨볼루션은 차원 축소 외에도 ReLU 활성화를 함께 사용해 이중 기능을 함.
    
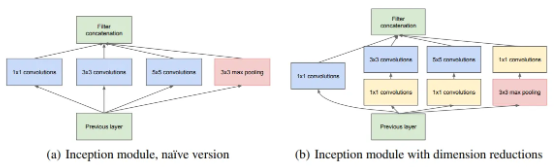
• 이와 같은 모듈들을 층층히 쌓은 구조가 Inception Network이고, 중간중간 stride가 2인 max pooling 레이어를 추가해 그리드의 해상도를 절반으로 줄이기도 함.

GoogLeNet

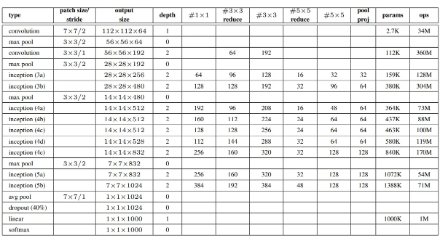
• Inception 모듈 내부를 포함해 모든 컨볼루션 연산에는 ReLU 활성화 함수가 사용됐으며, 네트워크에서 사용하는 receptive field 크기는 224*224이고, 입력은 mean subtraction을 적용한 RGB 컬러 채널
• #3×3 reduce와 #5×5 reduce는 33과 55 컨볼루션 이전에 적용되는 1*1 차원 축소 레이어의 필터 수
• pool proj은 풀링 이후 적용되는 1*1 프로젝션 레이어의 필터 수
• reduction/projection 레이어도 ReLU 활성화를 사용함.
  
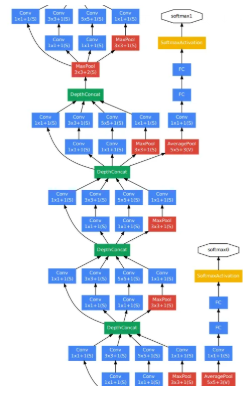
• 초기 단계부터 판별력을 높이고, 역전파되는 Gradient를 고려하고, 추가적인 정규화 효과 제공을 위해 auxiliary classifier를 추가하고, 학습 과정에선 loss가 전체 네트워크 손실에 가중치 0.3을 곱해 합산되나, 추론 시엔 auxiliary classifier를 제거하고 사용함.
• 이러한 auxiliary classifier는 필터 크기 55, stride 3인 평균 풀링 레이어, 차원 축소를 위한 필터 수 128개의 11 컨볼루션, 유닛 수 1024개의 FCN, 70% 드롭아웃 비율을 지닌 드롭아웃 레이어, 선형 레이어+소프트맥스 손실 함수로 구성됨.
  
  

Polyak averaging : 모델 파라미터들의 이동 평균(지금까지 지나온 파라미터 평균)을 계산하는 방법

• 일부 구현에선 5x5 대신 3x3을 두 번 포함해 5x5 컨볼루션의 효과를 냄
• 이후 버전들에선 연산량 절감을 위해 3x3 연산을 1x3, 3x1 커널로 나누어 연산하기도 함.

GoogLeNet(
  # 앞쪽 -> local한 특징 추출 + 계산량 줄임
  (conv1): BasicConv2d(
    (conv): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False) 
    (bn): BatchNorm2d(64, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
  )
  (maxpool1): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=True)  
  (conv2): BasicConv2d(
    (conv): Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
    (bn): BatchNorm2d(64, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
  )
  (conv3): BasicConv2d(
    (conv): Conv2d(64, 192, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
    (bn): BatchNorm2d(192, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
  )
  (maxpool2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=True)
  
  # Global한 특징 통합
  # 희소 구조를 밀집하게 근사하기 위해 브랜치를 나누고, 여러 스케일 정보를 뽑기 위해
  # 다양한 종류의 필터 사용
  (inception3a): Inception(
    (branch1): BasicConv2d(
      (conv): Conv2d(192, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn): BatchNorm2d(64, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
    )
    (branch2): Sequential(
      (0): BasicConv2d(
        (conv): Conv2d(192, 96, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(96, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicConv2d(
        (conv): Conv2d(96, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn): BatchNorm2d(128, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (branch3): Sequential(
      (0): BasicConv2d(
        (conv): Conv2d(192, 16, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(16, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicConv2d(
        (conv): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn): BatchNorm2d(32, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (branch4): Sequential(
      (0): MaxPool2d(kernel_size=3, stride=1, padding=1, dilation=1, ceil_mode=True)
      (1): BasicConv2d(
        (conv): Conv2d(192, 32, kernel_size=(1, 1), stride=(1, 1), bias=False)
        (bn): BatchNorm2d(32, eps=0.001, momentum=0.1, affine=True, track_running_stats=True)
      )
    
  )