이 글은 Coursera에서 제공하는 Andrew Ng 교수님의 Supervised Machine Learning : Regression and Classification 강의를 듣고 기록한 것입니다.

---

Gradient Descent(경사 하강법)이란?

Gradient Descent

 Gradient Descent이란, Cost Function $J_{(w,b)}$의 값이 최소가 되도록 w, b 값을 구하는 알고리즘을 의미한다.

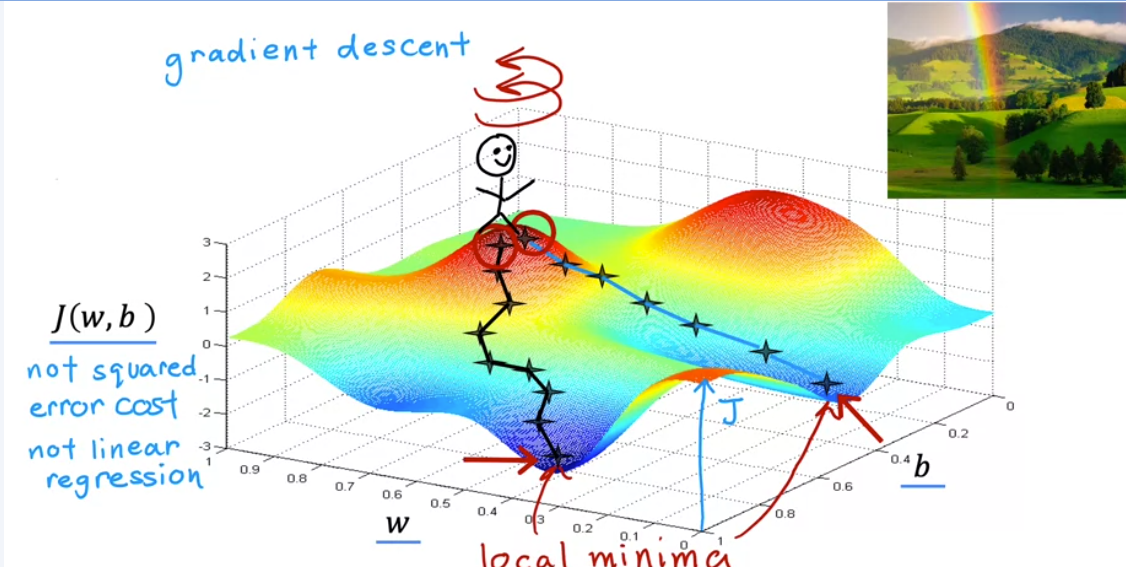
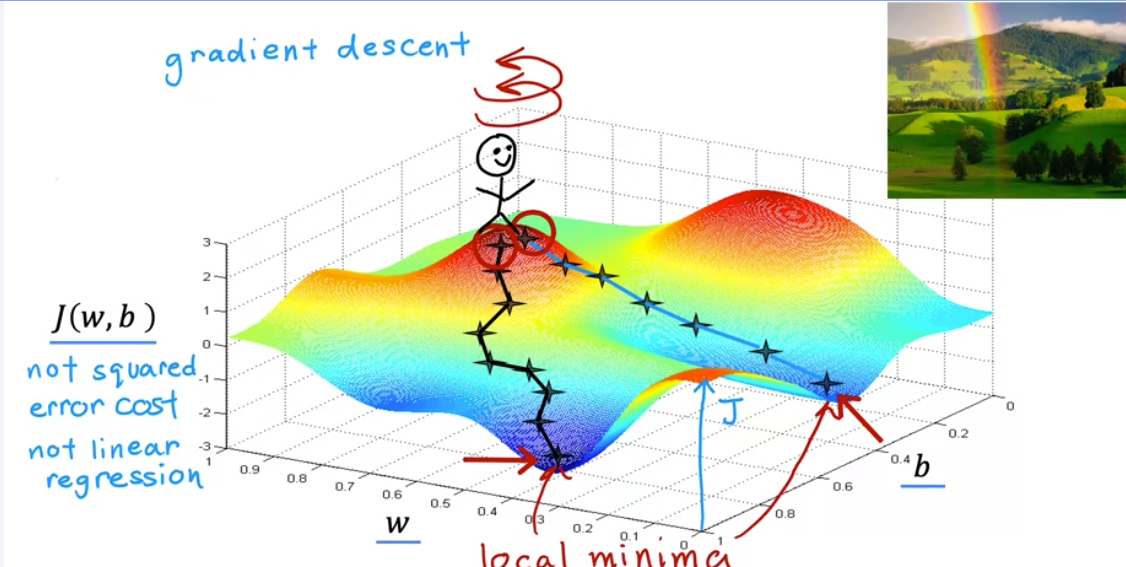
 아래의 사진에서처럼 3차원 그래프가 있다고 했을 때, 높은 지점을 언덕, 낮은 지점을 계곡이라고 생각해 보자. 여기서 임의의 지점 (w, b)를 시작점으로 잡고, 내려가면서 최소값(minimum)에 도달하는 과정을 경사하강법 알고리즘이라고 한다. 이때, 첫 번째 도달한 계곡의 위치, 두 번째 도달한 계곡의 위치는 각각 local minima라고 한다.

 이제 이것에 대해 더 자세히 살펴보자. 앞에서도 말했듯, Gradient Descent은 Cost Function $J_{(w,b)}$의 값이 최소가 되도록 w, b 값을 구하는 알고리즘이다. 그렇기 때문에 만약 비용 함수의 값이 최소가 아니라면, 일정한 식에 따라 w, b를 조정하고 Cost Function $J_{(w,b)}$가 최소가 되는지 확인하는 과정이 필요하다.

 그 과정은 아래의 사진과 같다.

 기존 w 값에서 Cost Function $J_{(w,b)}$를 기존 Cost Function $J_{(w,b)}$를 w에 대해 편미분한 값에 learning rate를 가리키는 α를 곱한 다음, 기존 w에서 이 값을 빼준다.
 b에 대해 계산하는 것도 b에 대해 편미분한다는 것으로 조건을 바꿔주는 것을 빼면 과정은 같다.

 이렇게 계산을 할 때 주의해야 할 점은, w와 b의 변경이 동시에 이뤄져야 한다는 것이다. 왜냐하면 위의 그림 오른쪽과 같이 w를 변경한 뒤 b를 계산하게 되면 이미 갱신된 w 값이 b의 계산에 들어가기 때문에, 부정확한 계산 결과가 나올 수 있다. 이로 인해 알고리즘의 성능에 문제가 생길 수 있으므로 이 둘을 반드시 동시에 변경해야 한다.

 그럼 이제, 이 수식에서 도함수가 어떻게 작동하는지를 더 직관적으로 살펴보도록 하자. 이때 사용하는 예시는 이전 시간에도 살펴보았던 w, b에서 b=0으로 설정되었을 때의 예시이다.

 일단, 우리가 도함수의 값을 구하기 위해선 먼저 기울기를 알아내야 한다. 왜냐하면 기울기는 함수 J의 도함수를 나타내는 값이기 때문이다. 따라서 아래의 사진에서처럼 기울기를 구하기 위한 접선을 그리고, 접선을 활용해 삼각형을 그린다. 이렇게 그려진 삼각형을 통해 높이/너비를 구해주면 이 값이 기울기가 된다.

 이러한 과정을 통해 우리는 아래의 사진처럼 초기값을 잡았을 때, 도함수의 결과값이 언제나 양수가 된다는 것을 알게 되었다. 따라서 이때 w의 값은 항상 줄어든다는 것을 알 수 있다.

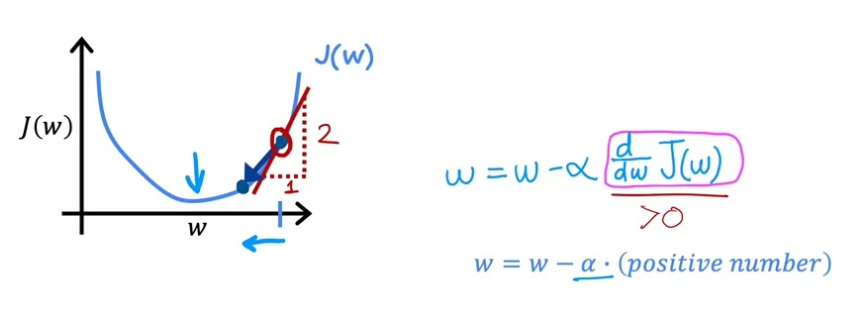
 초기값을 다음과 같이 잡았을 때도 원리는 같다. 똑같이 계산을 해주면 도함수의 결과값이 언제나 음수가 된다는 것을 알 수 있고, 이때 w의 값이 항상 증가하는 것을 알 수 있다.

Learning Rate

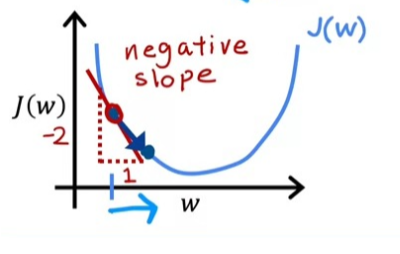
 Gradient Descent에 대한 직관적인 이해를 마쳤으니 이제 α 값에 대해서도 알아보자. 아래의 사진을 언덕이라 생각하고 내려간다 했을 때, α는 우리가 언덕에서 얼마만큼의 보폭으로 이동해서 맨 아래로 내려갈지를 결정하는 값이라고 생각하면 된다. 그렇기에 이 값이 너무 크거나, 너무 작으면 문제가 발생한다.

 만약 값이 0.0000001과 같이 아주 작다면, 결과적으로 Cost Function J는 최소값에 도달하긴 하겠지만, 너무 많은 단계들이 필요해지기 때문에 모델의 속도가 느려진다.

 또, 이 값이 너무 크다면, 아래의 그림의 2번째 그래프와 같이 Overshoot(초과이동)을 하면서 값이 minimum 값에 수렴하지 못하고 갈라지는 것을 확인할 수 있다. 결론적으로, 비용을 줄이지 못하고 늘리게 된다.

 그렇기에 우리는 너무 크거나 작지 않은, 최적의 α를 찾는 것이 중요하다.

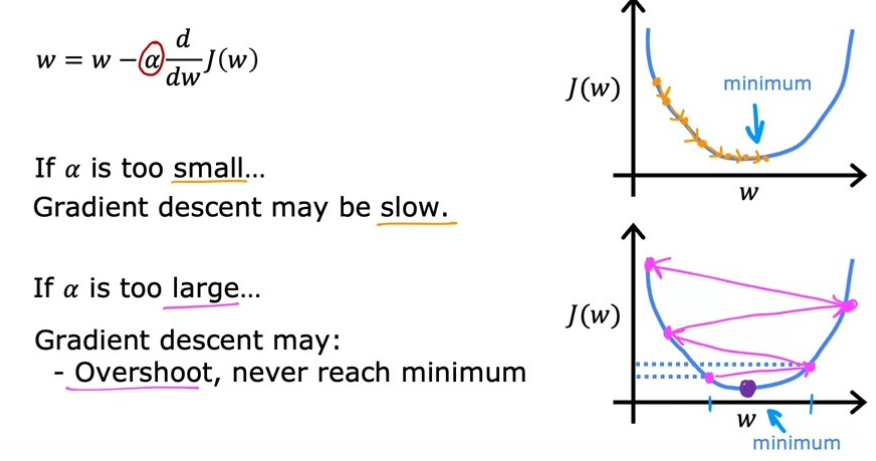
 또, 우리는 한 번 설정한 α를 학습 과정에서 변경하지 않고 고정시켜도 된다. 왜냐하면 Gradient Descent algorithm의 특성상, 초기에는 $J_{(w,b)}$의 기울기가 커서 경사하강이 큰 폭으로 진행되다가, 시간이 지나면서 w 값이 변경되고, 최소에 가까워지면서 기울기의 값이 점점 작은 폭으로 변하기 때문이다. 즉, 과정이 진행되면 될수록 천천히 minimum 값에 접근하게 된다는 것이다.

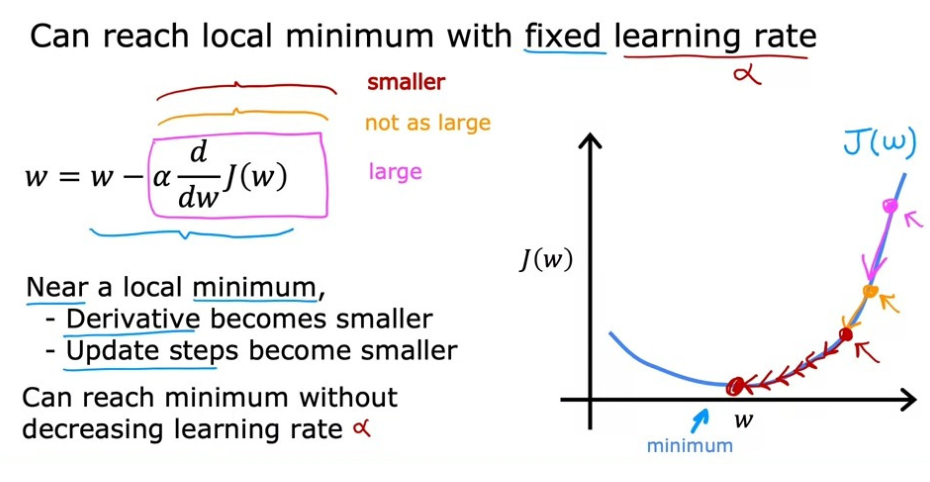
 이러한 특성으로부터 우리는 이 사실도 알 수 있다.

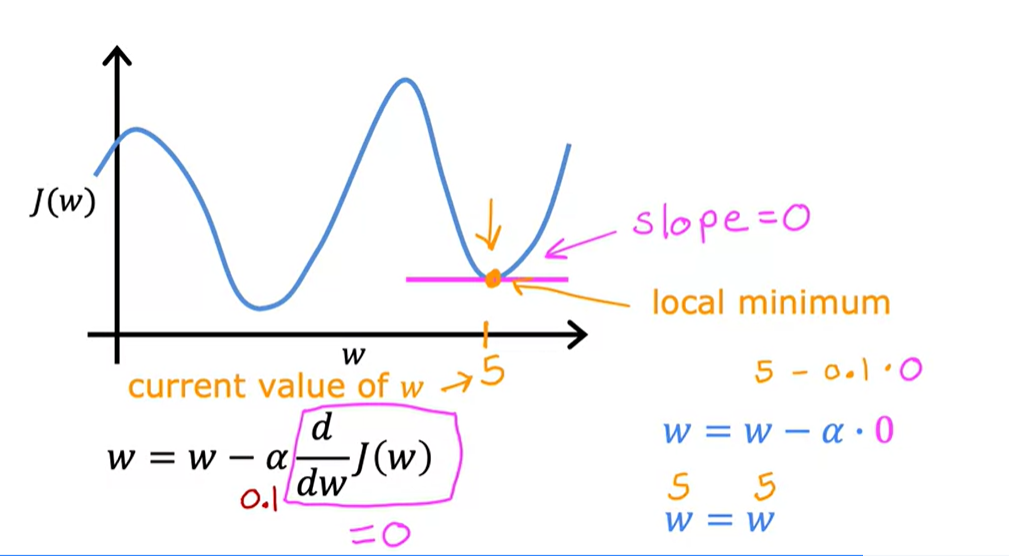
 만약, Gradient Descent algorithm을 진행하면서, local minimum 값에 도달했을 때, 우리는 global minimum 값에 도달하기 위해 경사하강의 과정을 한 단계 더 진행해도 될까, 하는 의문이 생길 수도 있다. 그러나 이미 local minimum 값에 도달한 상태에선 도함수의 결과값이 0이 된다. 따라서 경사하강의 과정을 더 진행하고자 해도 w 값이 항상 0이 되기 때문에 이 과정을 더 진행할 수 없다. 그렇기에 새로운 초기 위치를 찾아 다시 Gradient Descent algorithm을 수행하는 것이 좋다.

Gradient Descent for Linear Regression

 Linear Regression에 경사하강법을 적용하려면, 다음과 같은 알고리즘으로 정의할 수 있다.

 이러한 알고리즘으로 정의할 수 있는 이유는 미적분학과 관련이 있다. 미적분학을 이용하면 아래의 사진과 같이 도함수를 다르게 표현할 수 있기 때문이다.

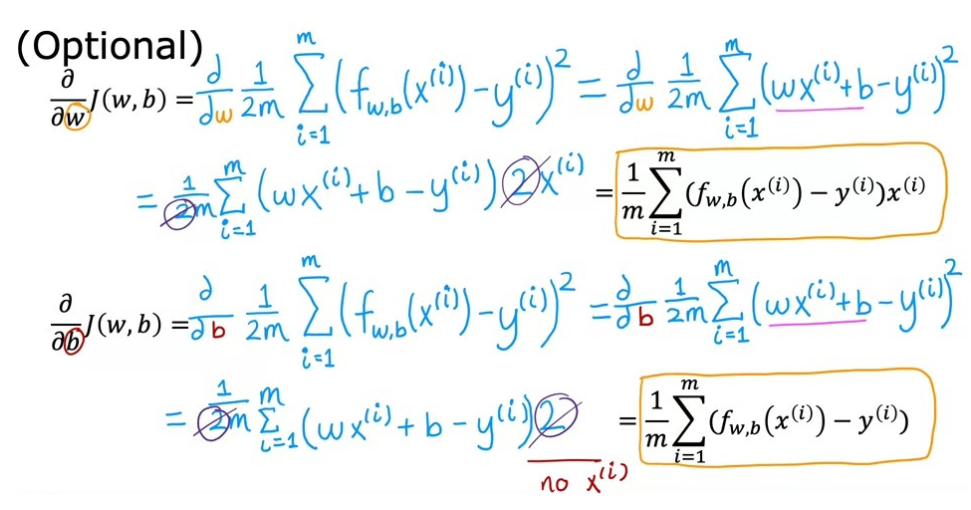
 따라서 Linear Regression에 경사하강법을 적용하고자 한다면, 아래의 알고리즘을 사용하면 되고, 이때도 마찬가지로 w, b는 동시에 업데이트해야 한다는 조건이 필요하다.

 Linear Regression에서 $J_{(w,b)}$를 구하면 항상 bowl shape의 3차원 그래프가 나온다. (이를 수학적으로 convex function이라고 이야기하기도 한다) 이러한 특성 때문에 여기서는 local minima가 하나이고, local minima와 global minima의 값이 같다. 따라서 경사하강을 진행할 때, α 값에 문제가 있는 게 아닌 이상 시작 지점에 상관 없이 언제나 그 결과가 global minima에 수렴한다.

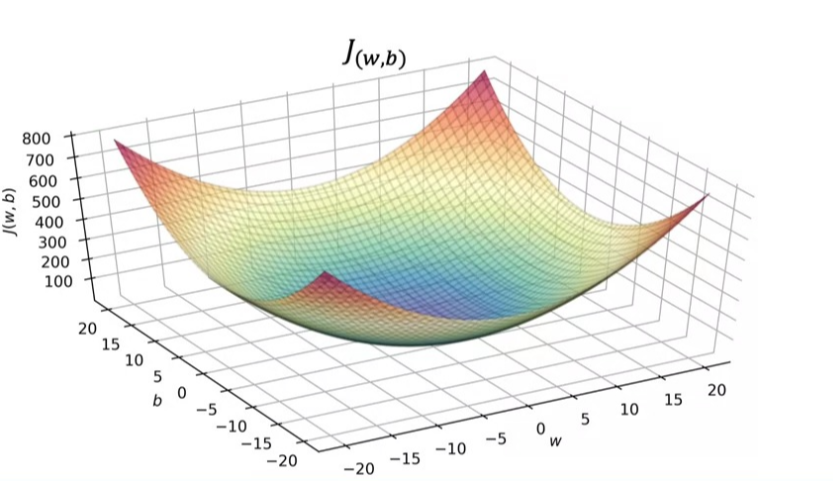
Running Gradient Descent

 지금까지 배운 경사하강법을 Batch gradient descent라고 이야기한다. Batch는 집단 혹은 무리라고 해석되는데, 알고리즘의 모든 단계에서 훈련 데이터의 일부가 아니라 모든 훈련 예제에 대해 Cost Function의 기울기를 구하기 때문에 이러한 이름이 붙었다.

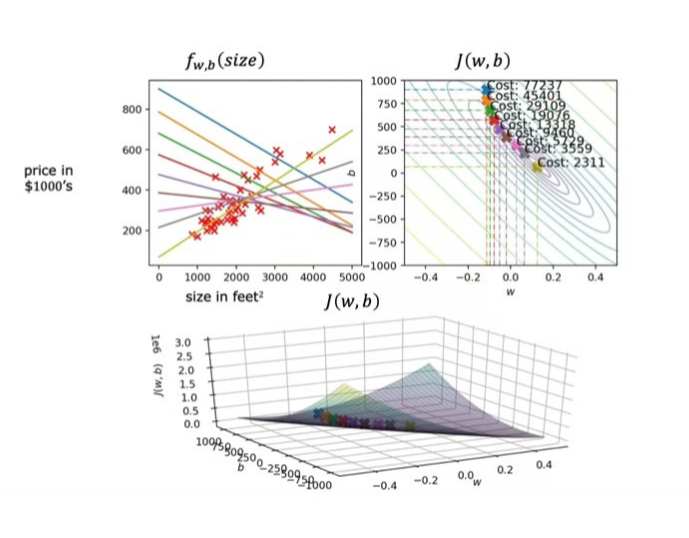
 아래의 사진은 최적의 값을 찾기 위해 w, b를 조정해 가면서 가장 작은 $J_{(w,b)}$의 값을 구하는 것을 나타낸다.