이 글은 Coursera에서 제공하는 Andrew Ng 교수님의 Supervised Machine Learning : Regression and Classification 강의를 듣고 기록한 것입니다.

---

Multiple Regression

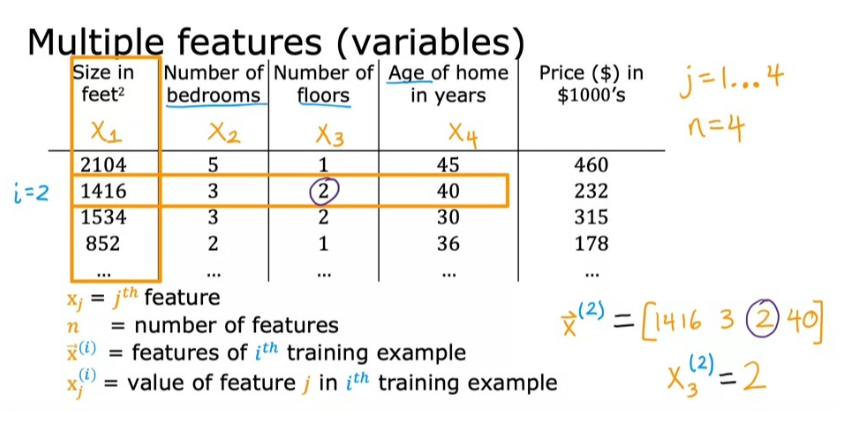
 일단, 지금까지 봐온 모델들은 feature가 하나일 때의 모델이었습니다. 하지만, 실제 머신러닝 학습에서는 한 가지 feature만 사용하지 않고, 다양한 features들을 사용합니다.

 예를 들어 아래의 사진과 같이 집의 사이즈, 침실 수, 층수, 집의 연식 등을 종합적으로 고려해서 결과값(가격)을 도출해낸다는 것이죠.

 그렇다면, 이때엔 어떠한 모델을 사용하는 것이 좋을까요?

 당연히 다양한 feature들에 대해서, 각각의 파라미터 값을 조절할 수 있어야 합니다. 아래의 사진과 같이요.

 이렇게 여러 개 여러 입력 특성을 가진 선형 회귀 모델을 Multiple Linear Regression(다중 선형 회귀)라고 부릅니다.

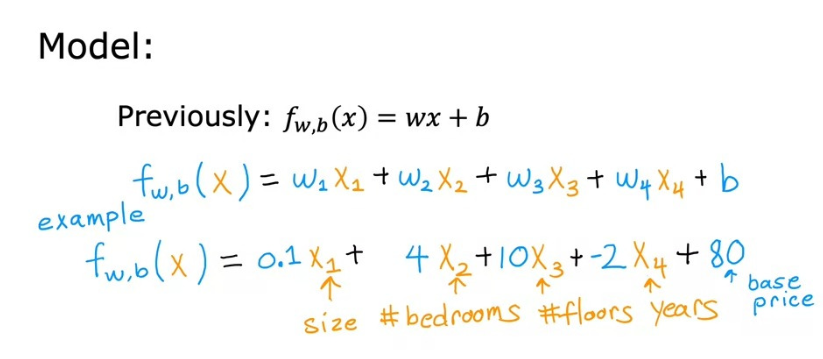
 위의 사진처럼 표현하면 단점이 있습니다. 값이 n 값이 100이나 1000일 때처럼 큰 값일 때, 모든 값을 표현하기 힘들어집니다. 그래서 우리는 Vectorization을 활용합니다.

Vectorization

 Vectorization은 파라미터 w와 input x를 벡터 형식으로 구성한 뒤, 이 둘을 dot product하는 방식으로, NumPy dot 함수를 통해 구현이 가능합니다.

 이 방법을 활용하면, 기존의 for 루프를 활용하는 방식이나, 모든 값을 직접 구하는 방식보다 훨씬 더 빠르고 효율적으로 실행된다는 장점이 있습니다. 왜냐하면 NumPy dot 함수는 내부적으로 병렬 하드웨어를 사용한 병렬 프로세스 처리가 가능하기 때문입니다.

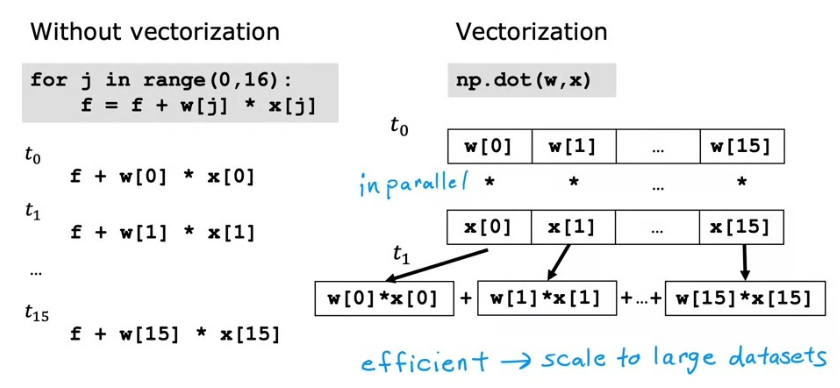
 백그라운드에서 이 구현이 어떻게 작동하는지를 보면 아래의 사진과 같습니다. for 루프를 사용한 경우엔 각각의 계산이 순차적으로 이뤄져서 불편함이 있는 반면에, 벡터화를 이용하면 n개의 값을 한 번에 병렬로 동시에 처리하기 때문에 계산이 for 루프보다 빠르게 이뤄집니다.

 이러한 벡터화는, 수천 개 이상 training set이 있을 때 더 중요합니다. 작은 training set으로 확인했을 땐 속도 차이가 크지 않아 보이지만, 큰 training set을 가지고 확인했을 땐 학습을 한 달 동안 시키느냐, 1~2일 동안 시키느냐와 같은 엄청난 차이를 보이기 때문입니다.

Gradient Descent for Multiple Regression

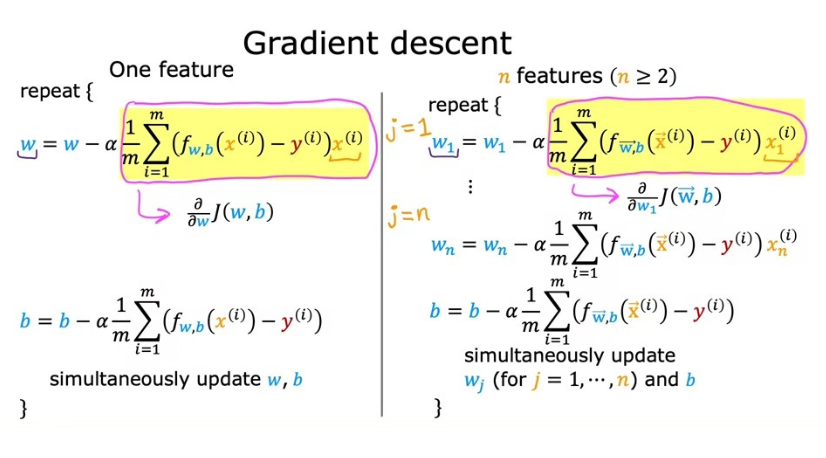
 그렇다면, 이제 이러한 벡터화를 이용해 다중 선형 회귀의 경사하강법을 구현해 보면 다음과 같습니다.

 이전에 배운 경사하강법 표기법과의 차이는 w, x의 값이 여러 개이기 때문에 벡터로 표현되고, 이 두 값이 dot product로 계산된다는 점입니다.

 또, 도함수의 항에 대해서도 살펴보면, 하나의 feature 값이 존재할 때와는 다르게, n개의 모든 w 값에 대해 편미분을 하고, learning rate와 곱한 뒤에 모든 w 값, 그리고 하나의 b 값을 동시에 업데이트한다는 점에서 차이가 존재하는 걸 확인할 수 있습니다. (이전에는 하나의 w, 하나의 b 값만 존재했기에 여러 개 w 값을 고려할 필요가 없었습니다)

 이렇게 하면 매개변수를 동시에 조절하면서 최적의 값을 찾아간다는 경사하강법의 기본적인 원칙을 만족하면서도 최적의 w, b 파라미터 값을 찾을 수 있습니다. 이게 다중 선형 회귀에서의 경사하강법입니다.