이 글은 Coursera에서 제공하는 Andrew Ng 교수님의 Supervised Machine Learning : Regression and Classification 강의를 듣고 기록한 것입니다.

---

Linear Regression

 Linear Regression은 Regression model의 한 예시로, 단지 데이터를 직선에 맞추는 것을 의미한다.

 Linear Regression은 생각보다도 훨씬 더 많이 사용되는 방식인데, 그 이유는 표현하기 상대적으로 쉽고 간결하기 때문에 더 복잡한 Non-linear 모델을 얻기 위한 토대가 되는 선으로 사용하기 좋기 때문이다.

 아래의 사진은 Linear Regression의 적용 예시이다. 만약 내가 부동산 주인이고, 손님이 집을 얼마에 팔 수 있는지 물어본다면, 나는 내가 가진 데이터셋을 활용해 비용을 산출해야 한다. 이를 위한 방법 중 하나가 선형 회귀 모델을 만드는 것이다.

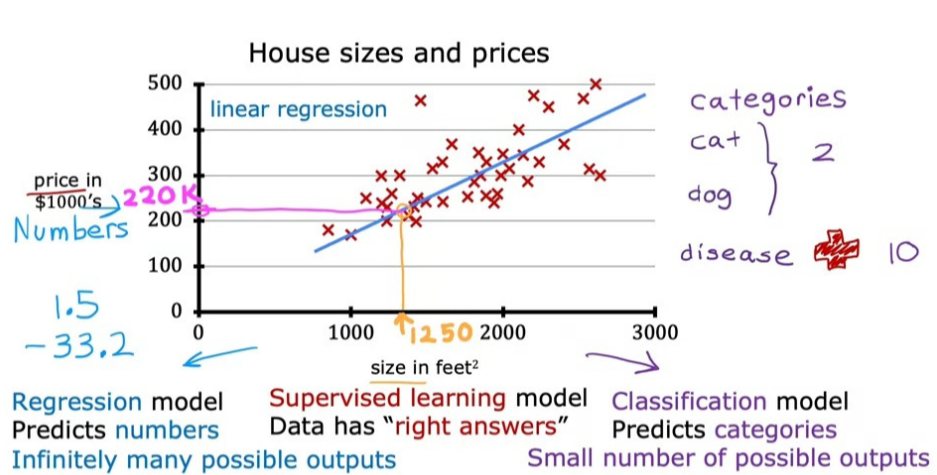
 이러한 Regression model은 input과 right answer(price)를 통해 예측하므로 Supervised learning에 해당한다.

Terminology

• Training set : Data used to train the model, 즉 모델 학습에 사용되는 데이터를 의미한다.
• x : input을 나타내는 표준 표기법으로, input variable, feature, input feature로도 부른다.
• y : output을 나타내는 표준 표기
• m : number of training examples
• $(x, y)$ : single training example (ex) (2104, 400) - 아래 Data Table 기준 확인
• $(x^{(i)}, y^{(i)})$ : ith training example (ex) $(x^{(1)}, y^{(1)})$ = (2104, 400)
  - 이때, $x^{(2)}$는 $x^2$와는 다른 개념이다. i는 단지 training set을 가리키는 index일 뿐, 지수가 아니다.

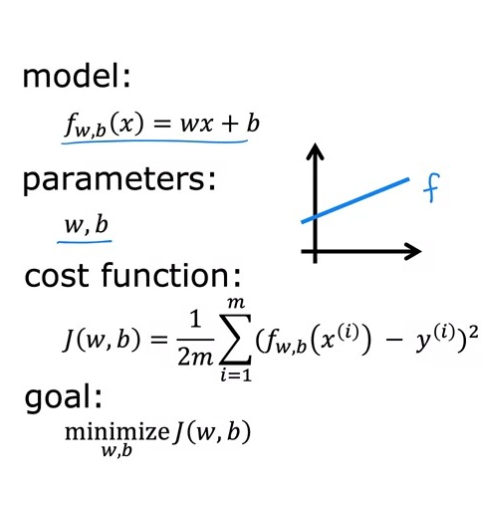
Cost Function

 Cost Function에 대해 알아보기 전 알아야 할 기본적인 개념을 살펴보자.

 Supervised learning에서는 features와 targets가 담긴 데이터셋을 통해 Learning algorithm을 만들어내고, 이를 통해 함수 f를 만든다. 이 함수를 우리는 model이라고 부른다.

 이러한 함수 f는 새로운 입력값 x를 받고,이에 대한 예측값 $\hat{y}$를 추정하는 역할을 한다.

 모델 f에는 다음과 같은 수학적 공식이 적용된다.

  이때, w, b에 선택된 값이 x를 기반으로 $\hat{y}$을 결정한다. 또한, 이 식은 일차함수와 같은 꼴이라서 이를 Univariate linear regression이라고도 한다.
 참고로, 이 공식에서 $f_w,_b(x)$라는 표현은 $f(x)$와 같은 표현이다. 그렇기에 둘 중 무엇으로 표현하든 상관이 없다.

 그렇다면 이제 Cost Function에 대해 자세히 알아보자.

 일단, Cost Function에서 사용하는 Model은 $f_w,_b(x) = wx + b$이다. 이때, w와 b는 parameters 값으로, w, b에 대해 선택한 값에 따라 다른 함수 f를 생성한다. 그리고 함수 f는 값에 따라 다른 선을 그래프에 생성한다.

 그림으로 살펴보면 좀 더 직관적으로 이해할 수 있다.

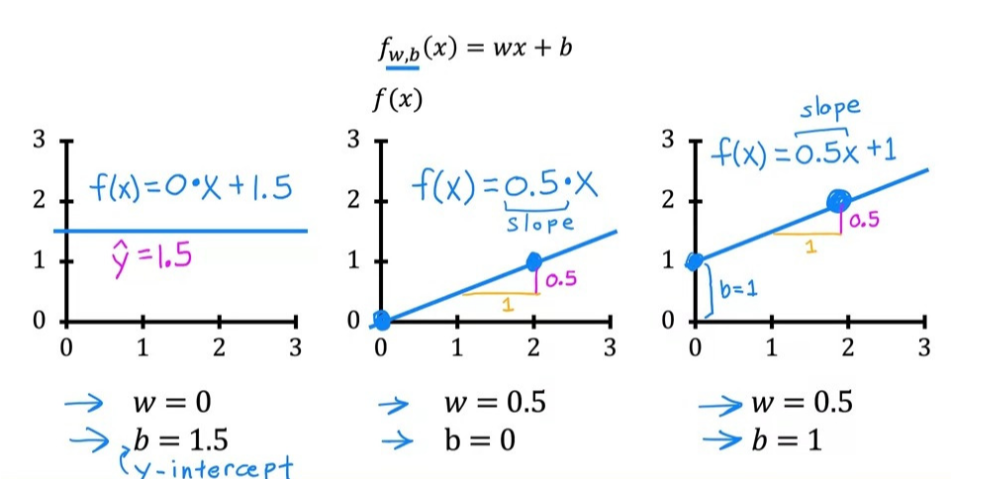
 이렇게 w, b 값에 따라 함수가 변화하는 것을 확인했다. 이제 우리가 해야할 일은, 이를 이용해서 함수 f에서 얻은 직선이 $(x^{(i)}, y^{(i)})$에 잘 맞도록(예측의 정확도가 높도록) w, b의 값을 선택하는 것이다. 즉, 새롭게 입력 받은 x에 대한 예측 결과 $\hat{y}$가 기존 데이터 셋의 right answer과 최대한 비슷하거나 근접하도록 값을 조절해야 한다는 것이다.

 따라서 $f_w,_b(x)$와 y 값의 오차가 최소가 되도록 w, b의 값을 찾아야 한다. 우리는 이를 위해 Cost Function을 사용한다. 이를 통해 예측 값이 target 값으로부터 얼마나 멀리 떨어져 있는지 측정한다. 이 Cost Function이 작을수록, 실제 결과값과 유사한 예측값을 도출한다.

 Cost Function을 작게 만들기 위해선 결국 w, b 값을 조절해 가면서 작은 값을 도출해 내야 한다. 왜냐하면 Cost Function을 구하기 위해선 $\hat{y}$에서 y를 뺀 값인 error를 구해야 하기 때문이다.

 이를 정리하면 다음과 같다.

 Cost Function에서 b=0으로 가정하고, 단순한 형태의 그래프로 표현했을 때 다음과 같이 수프 모양의 그래프가 나온다. 이때의 목표도 마찬가지로 w 값을 조절하여 Cost Function J(w)를 최소화하는 w를 찾는 것이므로 여기서 w는 1을 선택하는 것이 좋다.

 만약 b가 0이 아닌 값을 지닌다면 w와 b 값을 모두 그래프에 표현해야 하기 때문에 그래프는 다음과 같이 3차원의 형태를 지닌다.

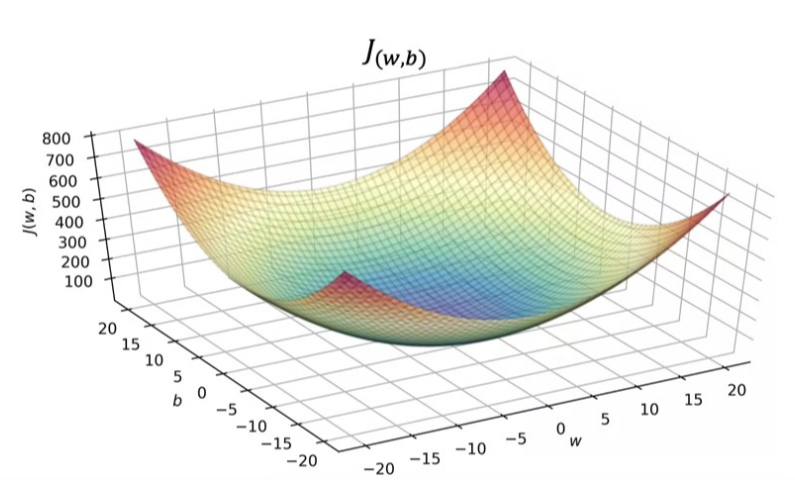
 그런데, 이 3차원 그래프를 통해 w, b 값을 선택하고자 하면, 조금 복잡한 부분이 있다. 그래서 우리는 이걸 좀 더 직관적으로 파악하기 위해 등고선도를 활용한다.

 등고선도는 3D 그래프를 위에서 보는 것과 비슷한 형태로, 등고선이 같으면 w, b 값이 달라도 같은 J 값을 지닌다.

 또, 등고선도에서는 타원의 중심이 J의 minimum 값을 가리킨다. 따라서 우리는 아래의 사진과 같이 J가 최대한 타원의 중심에 오도록 w, b 값을 선택하여야 한다.

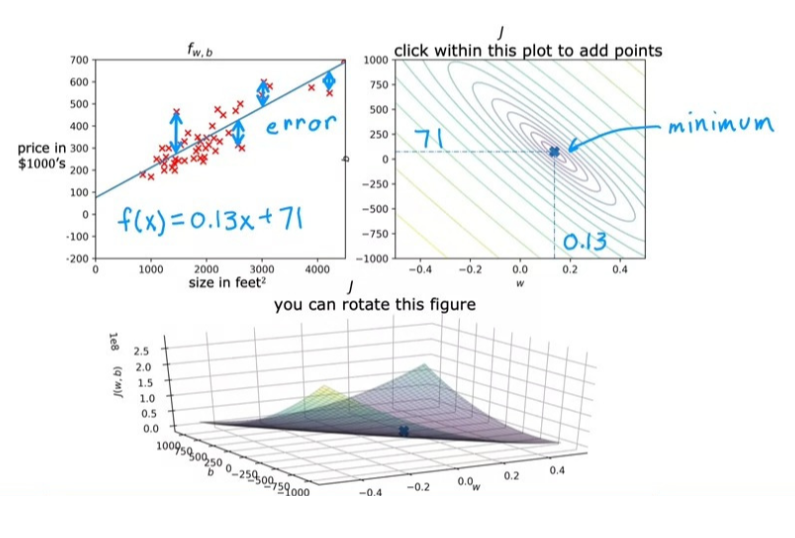
 사실 이렇게 직접적으로 찾는 방법 말고 J의 값이 최소화되는 w, b 값을 자동으로 찾아주는 알고리즘이 있는데, 이를 경사하강법이라고 한다. 이는 다음 시간에 더 자세히 다루게 될 것이다.