1. 자기 지도 학습 복습 및 최신 동향 (Self-Supervised Learning Recap)

• 자기 지도 학습 (Self-Supervised Learning, SSL) 패러다임: 레이블(Labels) 없이 데이터로부터 직접 구조를 학습하려는 흥미로운 접근 방식이다.
• 전형적인 구조: 레이블이 없는 대규모 데이터셋(X)을 인코더(Encoder)에 통과시켜 특징 표현(Feature representation)을 추출하고, 디코더(Decoder)를 통해 이 특징으로부터 무언가를 예측한다.
• 프리텍스트 태스크 (Pretext Task): 사람의 어노테이션(Annotation) 없이 시스템 전체를 훈련할 수 있도록 고안된 태스크이다.
• 2단계 절차 (Two-Stage Procedure):
  1. 대규모 데이터에 대해 자기 지도 학습 태스크로 인코더-디코더를 학습시킨다.
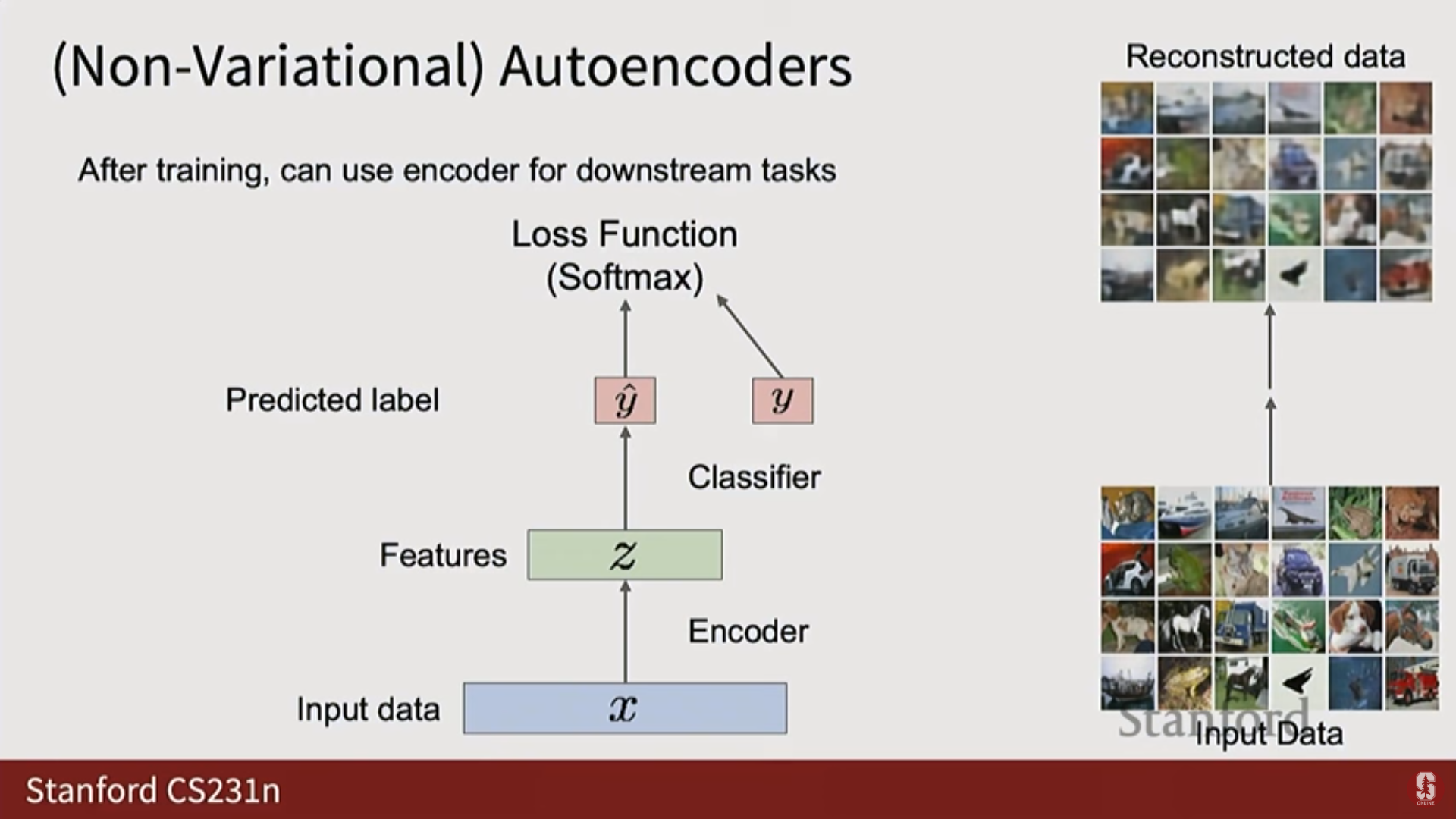
  2. 디코더를 제거하고, 새로운 작고 가벼운 완전 연결 신경망(Fully Connected Network) 등을 연결하여 다운스트림 태스크(Downstream tasks)에 대해 적은 양의 레이블 데이터로 학습시킨다.
• 목표: 레이블이 없는 수백만 또는 수십억 개의 대규모 데이터셋을 통해 이미지 또는 데이터의 일반적인 구조에 대한 지식(Generic knowledge)을 학습하고, 이 지식을 적은 레이블을 가진 다운스트림 태스크로 전이(Transfer) 시키는 것이다.
• 프리텍스트 태스크의 종류:
  • 회전 (Rotation): 이미지를 회전시키고 모델에게 회전된 정도를 예측하도록 요청한다.
  • 재배열 또는 직소 퍼즐 풀기 (Rearrangement or solving jig-saw puzzles): 이미지를 패치(Patches)로 자르고 원래 이미지에서 패치들의 상대적 배열을 예측하도록 요청한다.
  • 재구성 또는 인페인팅 (Reconstruction or inpainting): 입력 이미지의 일부를 삭제하고 모델에게 그 부분을 채우도록 요청한다.

1) 대조 학습 (Contrastive Learning)

• 대조 학습은 매우 성공적인 자기 지도 학습의 또 다른 형식이다.
• 핵심 아이디어: 유사한 쌍(Similar pairs)은 서로 당기고, 비유사한 쌍(Dissimilar pairs)은 서로 밀어낸다.
• SimCLR (A Simple Framework for Contrastive Learning of Visual Representations):
  • 입력 이미지(레이블 없음)에 두 개 이상의 무작위 변환(Random transformations)을 적용한다.
  • 모든 변형된 버전을 특징 추출기(Feature extractor, 예: ViT, CNN)에 통과시켜 특징 벡터를 얻는다.
  • $4N^2$ 유사도 행렬: $N$개의 이미지에 대해 2개의 변형을 적용하면 총 $2N$개의 샘플이 나오며, 이 샘플 간의 모든 쌍별 유사도를 계산하여 $2N \times 2N$ 행렬을 구성한다.
  • 원래 이미지에서 파생된 두 증강(Augmentation) 샘플은 서로 당기고(Pull together), 다른 원본 이미지에서 파생된 쌍은 서로 밀어낸다(Push apart).
  • 심화 내용 - SimCLR의 한계: SimCLR 설정은 좋은 수렴을 얻기 위해 상당히 큰 배치 크기(Large batch size) 를 요구한다. 이는 네트워크에 충분히 어려운 학습 신호를 제공하기 위함이며, 대규모 분산 학습(large scale distributed training) 기술이 필요해진다.

2) 모멘텀 대조 (Momentum Contrast, MOCO)

• 배경 및 동향: SimCLR의 거대한 배치 크기 요구 사항을 피하기 위해 고안되었다.
• 기술적 배경:
  • 훈련 반복마다 거대한 배치 크기를 사용하지 않기 위해, 이전 훈련 반복에서 얻은 음성 샘플(Negatives)의 큐(Queue) 를 유지한다.
  • 현재 배치($X_{query}$)는 일반 인코더(Encoder Network)를 통과시킨다.
  • 이전 히스토리 배치($X_{key}$)는 모멘텀 인코더 (Momentum Encoder) 를 통과시킨다.
  • 모멘텀 인코더에는 역전파(Backpropagation)를 수행하지 않는데, 이는 데이터 양이 너무 많아 GPU 메모리에 맞출 수 없기 때문이다.
  • 가중치 업데이트: 일반 인코더는 경사 하강법(Gradient descent)을 통해 학습되지만, 모멘텀 인코더의 가중치는 경사 하강법이 아닌, 지수 이동 평균(Exponential Moving Average, EMA) 방식으로 업데이트된다.
    $W_{momentum} \leftarrow 0.99 \cdot W_{momentum} + 0.01 \cdot W_{encoder}$
  • 이 방식을 통해 매 반복마다 거대한 음성 샘플 배치가 필요하지 않으면서도 자기 지도 표현 학습을 달성할 수 있다.

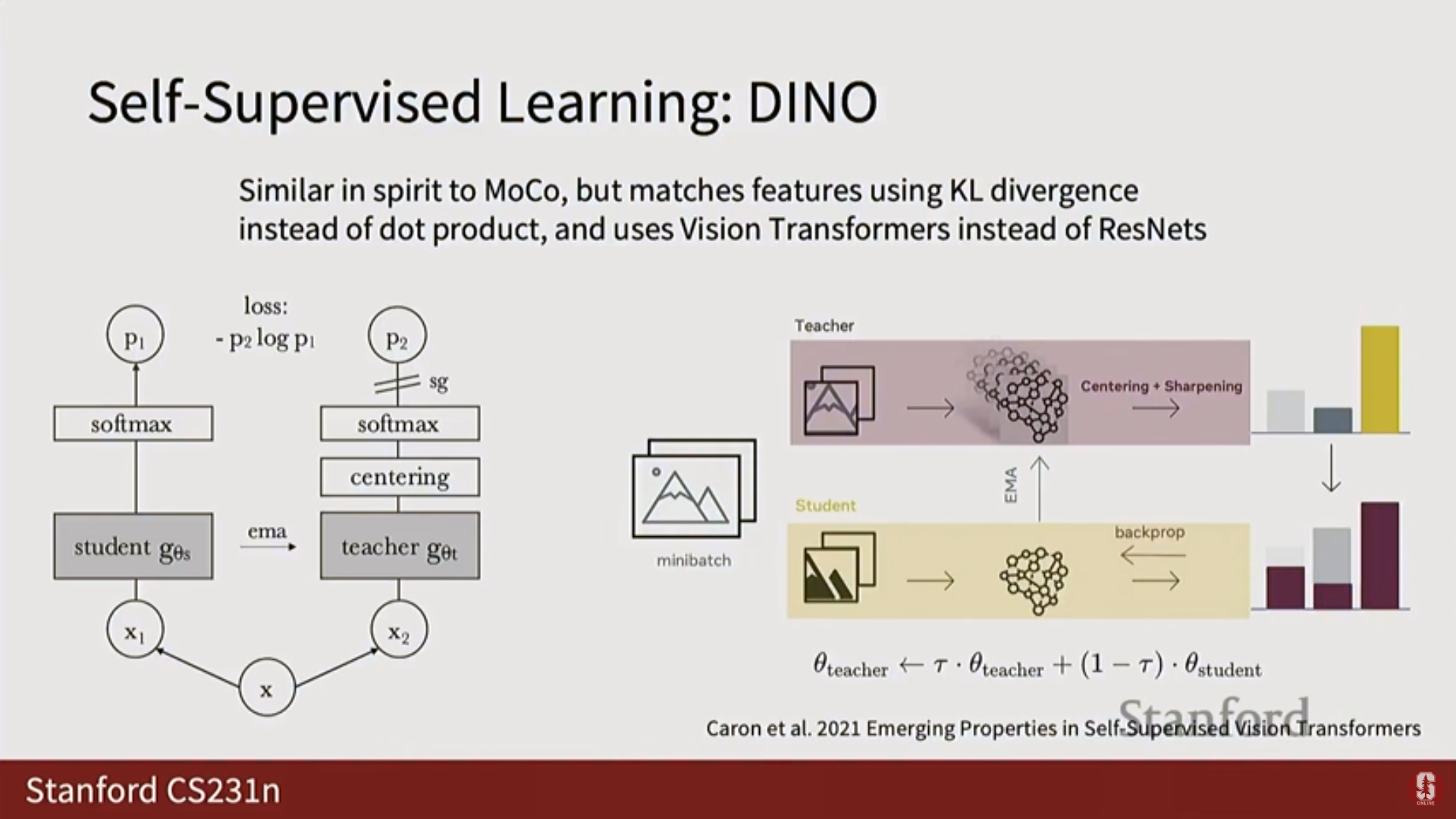
3) DINO 및 DINOv2

• DINO (Data-efficient Image Transformers): MOCO와 유사하게 모멘텀 인코더를 사용하지만, 손실 함수로 소프트맥스(softmax) 대신 KL 발산(KL divergence) 손실을 사용한다.
• 심화 내용 - DINOv2 (최신 동향):
  • DINOv2는 현재 실무에서 자기 지도 특징 추출에 널리 사용되는 매우 강력한 모델이다.
  • DINOv2의 핵심은 훈련 데이터의 규모를 크게 확장했다는 점이다. 기존 SSL 접근 방식이 ImageNet 데이터셋(100만 이미지)에 대해 훈련된 반면, DINOv2는 약 1억 4200만 이미지의 훨씬 더 큰 훈련 세트로 확장되었다.
  • 이는 더 큰 네트워크, 더 큰 데이터, 더 많은 컴퓨팅 자원(Flops)을 선호하는 딥러닝의 경향을 반영한다.
  • DINOv2는 강력한 자기 지도 특징을 제공하며, 다운스트림 태스크를 위한 미세 조정(Fine-tuning)에 사용된다.

---

2. 생성 모델 (Generative Models)

• 생성 모델은 지난 몇 년간 급격히 발전한 딥러닝 분야이다.
• 10년 전만 해도 제대로 작동하지 않았지만(저해상도, 흐릿함), 이제는 언어 모델(Language models)이나 이미지 및 비디오 생성 모델 등 다양한 분야에서 매우 잘 작동한다.
• 근본적인 아이디어: 데이터에 대해 생각하는 방식과 모델링 접근 방식은 크게 변하지 않았지만, 더 나은 컴퓨팅, 더 안정적인 훈련 방법, 더 큰 데이터셋, 그리고 분산 훈련 능력이 발전의 주요 동력이었다.

1) 지도 학습 vs. 비지도 학습 (Supervised vs. Unsupervised Learning)

(1) 지도 학습 (Supervised Learning)

• 데이터셋이 입력(X)과 타겟/레이블(Y)의 쌍으로 이루어져 있다.
• 목표: 입력 데이터 X로부터 타겟 Y로 매핑하는 함수를 학습하는 것이다.
• 예시:
  • 이미지 분류: 입력 X(이미지) $\to$ 출력 Y(레이블).
  • 이미지 캡셔닝: 입력 X(이미지) $\to$ 출력 Y(설명 텍스트).
  • 객체 탐지: 입력 X(이미지) $\to$ 출력 Y(바운딩 박스, 카테고리 레이블).
  • 분할: 입력 X(이미지) $\to$ 출력 Y(픽셀별 레이블).

(2) 비지도 학습 (Unsupervised Learning)

• 레이블 없이 오직 데이터 샘플 X만 가지고 있다.
• 목표: 데이터로부터 어떤 종류의 구조(Structure)를 발견하거나 좋은 표현(Good representations)을 학습하는 것이다.
• 예시:
  • K-평균 군집화 (K-means clustering): 데이터 내의 군집(Clusters) 구조를 식별.
  • 차원 축소 (Dimensionality reduction, PCA): 데이터 구조를 설명하는 저차원 부분 공간(Subspace) 또는 매니폴드(Manifold)를 발견.
  • 밀도 추정 (Density estimation): 데이터 샘플을 발생시킨 확률 분포(Probability distribution)를 파악.

2) 생성 모델 vs. 판별 모델 (Generative vs. Discriminative Models)

• 생성 모델과 판별 모델은 본질적으로 확률적(Probabilistic) 이다.
• 핵심 개념 - 정규화 제약 (Normalization Constraint): 확률 분포(Probability distribution) 또는 밀도 함수(Density function) $P(X)$는 전체 가능한 입력 $X$ 공간에 대해 적분하면 반드시 1이 되어야 한다.
• 이 정규화 제약은 모든 가능한 $X$들이 확률 질량(Probability mass) 을 얻기 위해 서로 경쟁하게 만든다. 만약 한 $X$의 확률을 높이면 다른 $X$들의 확률은 필연적으로 낮아져야 한다.
  

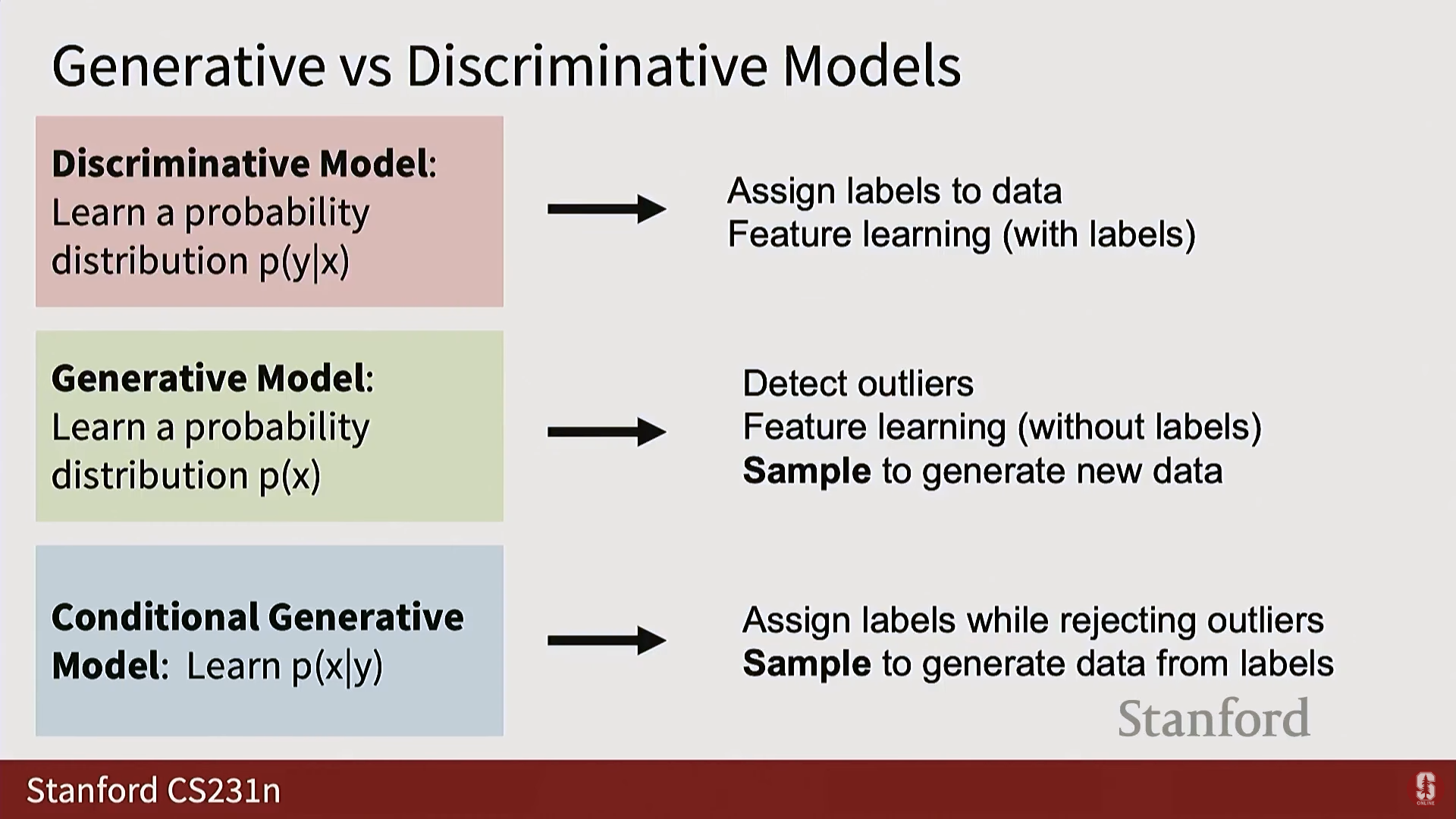
(1) 판별 모델 (Discriminative Model)

• 학습 대상: $P(Y|X)$ (입력 이미지 $X$가 주어졌을 때 레이블 $Y$에 대한 확률 분포).
• 경쟁: 각 입력 $X$에 대해 모델은 가능한 모든 레이블에 대한 확률 분포를 예측한다. 이미지들 사이에서는 확률 질량에 대한 경쟁이 없다.
• 한계: 불합리한 입력(Unreasonable inputs)을 거부할 능력이 없다. 예를 들어, 레이블 공간이 '고양이'와 '개'로 고정된 경우, 추상 미술 작품을 입력해도 시스템은 반드시 '고양이' 또는 '개'에 대한 분포를 출력해야 한다.
  

(2) 생성 모델 (Generative Model)

• 학습 대상: $P(X)$ (가능한 모든 이미지 $X$에 대한 분포).
• 경쟁: 우주에 존재하는 가능한 모든 이미지가 확률 질량을 얻기 위해 서로 경쟁한다.
• 심화 내용: 이는 모델이 세상의 구조에 대해 매우 깊고 철학적인 질문에 답하도록 강제한다 (예: 다리가 세 개인 개 이미지는 팔이 세 개인 원숭이 이미지보다 높은 확률을 가져야 하는가?).
• 특징: 모델이 불합리한 입력(unreasonable input) 에 대해 낮은 또는 0의 확률 질량을 할당함으로써 해당 입력을 거부할 수 있는 능력을 갖는다.
  

(3) 조건부 생성 모델 (Conditional Generative Model)

• 학습 대상: $P(X|Y)$ (어떤 레이블 $Y$가 주어졌을 때 이미지 $X$에 대한 조건부 분포).
• 경쟁: 레이블 $Y$ (예: '고양이', '개') 각각에 대해, 모델은 가능한 모든 이미지 사이에서 별도의 경쟁을 유도한다.
• 복잡성: 조건 신호 $Y$가 텍스트 설명이나 다른 이미지와 텍스트의 조합처럼 풍부할 경우, 모델은 매우 복잡하고 정의하기 어려운 문제를 해결해야 한다.
  

(4) 베이즈 규칙을 통한 관계 (Relationship via Bayes' Rule)

• 판별 모델, 비조건부 생성 모델, 그리고 레이블에 대한 사전 분포($P(Y)$)가 있다면, 이들을 결합하여 조건부 생성 모델을 만들 수 있다.
• 수식:
  $\text{P(X|Y)} = \frac{\text{P(Y|X)P(X)}}{\text{P(Y)}}$
• 이론적으로는 이들이 서로 관련되어 있지만, 실제로는 조건부 생성 모델을 처음부터 학습하는 경우가 많다.
  

3) 확률적 모델의 용도 (Use Cases of Probabilistic Models)

모델 종류	주요 용도	실용적 유용성
판별 모델 ($P(Y\|X)$)	데이터에 레이블 할당, 특징 학습(Feature Learning).	높음.
비조건부 생성 모델 ($P(X)$)	이상치 탐지(Outlier detection), 특징 학습 (성공적이지 않음). 새로운 샘플 X 생성 (제어 불가능).	낮음. 샘플링 시 무엇을 생성할지 제어할 수 없어 실용성이 떨어진다.
조건부 생성 모델 ($P(X\|Y)$)	이상치를 거부하며 레이블 할당, 레이블을 통해 새로운 데이터를 제어하며 샘플링/생성.	가장 유용함. 실제 훈련되고 사용되는 대부분의 생성 모델은 조건부 모델이다.

• 용어 혼란 주의: 문헌에서 '생성 모델(Generative Model)'이라는 용어는 종종 조건부 생성 모델을 포함하여 사용된다.
  

생성 모델의 필요성: 모호성 모델링 (Modeling Ambiguity)

• 생성 모델을 구축하는 주된 이유는 모델링하려는 태스크에 모호성(Ambiguity) 이 있을 때이다.
• 출력에 불확실성이 있을 때 (예: "핫도그 모자를 쓴 개의 사진을 만들어줘"라는 질의에 대해 가능한 수많은 출력 이미지), 생성 모델은 입력 신호에 조건화된 전체 출력 분포를 모델링한다.
• 예시:
  • 언어 모델링 (Language Modeling): 입력 텍스트($Y$)로부터 출력 텍스트($X$)를 예측한다. "생성 모델에 대한 짧은 운문 시를 써줘"라는 질의에는 수많은 가능한 시가 존재하며, 생성 모델은 그 전체 분포를 모델링한다.
  • 텍스트-이미지 생성 (Text to Image): 입력 텍스트($Y$)에 맞는 가능한 수많은 이미지를 생성한다.
  • 이미지-비디오 생성 (Image to Video): 주어진 이미지 이후에 일어날 수 있는 가능한 미래를 모델링하고 샘플링한다.

4) 생성 모델의 분류 (Taxonomy of Generative Models)

• 생성 모델 분야는 수학적 내용을 많이 포함하며, 확률 분포를 모델링하는 다양한 방식에 따라 분류된다.
  

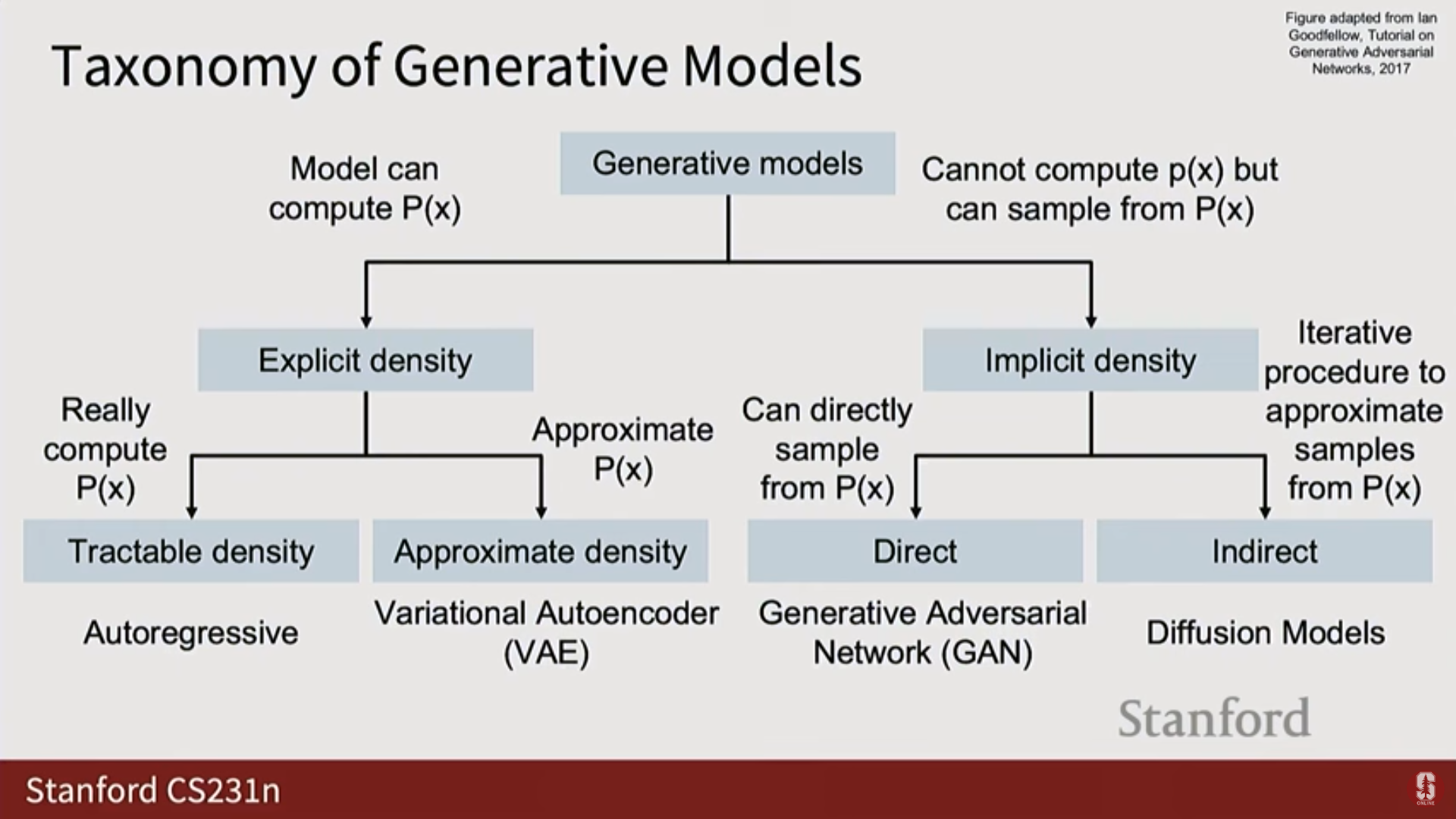
(1) 명시적 밀도 모델 (Explicit Density Models)

• 모델이 실제로 $P(X)$ 또는 $P(X|Y)$ 값을 계산할 수 있는 모델.

종류	특징	예시
명시적 (정확, Exact)	$P(X)$를 정확히 계산할 수 있다.	자기회귀 모델 (Auto-regressive Models).
명시적 (근사, Approximate)	$P(X)$의 근삿값 또는 하한(Lower bound)을 계산할 수 있다.	변이형 오토인코더 (Variational Autoencoders, VAEs).

(2) 암시적 밀도 모델 (Implicit Density Models)

• 모델에서 $P(X)$ 값을 직접 얻을 수 없지만, 확률 분포로부터 샘플링(Sampling) 할 수 있는 모델.

종류	특징	예시
암시적 (직접 샘플링)	단일 네트워크 평가로 샘플을 생성할 수 있다.	적대적 생성 신경망 (Generative Adversarial Networks, GANs).
암시적 (간접/반복적 샘플링)	샘플을 얻기 위해 반복적인 절차(Iterative procedure)가 필요하다.	확산 모델 (Diffusion Models) (다음 강의에서 다룰 예정).

---

3. 자기회귀 모델 (Auto-regressive Models)

1) 최대 우도 추정 (Maximum Likelihood Estimation, MLE)

• 생성 모델의 기본 목표 중 하나는 최대 우도 추정이다.
• 개념: 주어진 유한한 데이터 샘플 셋에 대해, 데이터셋을 가장 그럴듯하게(Most likely) 만드는 모델 가중치(Weights)를 찾는 것이다.
• 우도 (Likelihood) vs. 확률 (Probability):
  • 확률은 분포가 고정된 상태에서 $X$가 변할 때 $P(X)$가 어떻게 변하는지 본다.
  • 우도는 샘플 $X$가 고정된 상태에서 분포 자체(가중치 $W$)를 변화시키며 해당 샘플들의 확률 밀도가 어떻게 변하는지 본다.
• 가정: 우리가 보고 있는 데이터는 우주가 생성한 알려지지 않은 참 확률 분포 $P_{data}$로부터 샘플링되었다고 가정한다. 우리는 유한한 샘플을 통해 $P_{data}$를 발견하려 한다.
• 로그 우도 트릭 (Log Likelihood Trick):
  1. 데이터가 독립적이고 동일하게 분포(i.i.d.) 되었다고 가정하면, 결합 분포를 개별 샘플의 우도의 곱으로 분해할 수 있다.
  2. 로그($\log$) 함수는 단조 함수(Monotonic function)이므로, 우도를 최대화하는 것은 로그 우도를 최대화하는 것과 같다.
  3. 로그를 취하면 곱셈이 덧셈으로 바뀌어 계산이 편리해진다.
     $\text{Maximize} \log P(\mathbf{X} | W) = \sum_{i=1}^N \log P(X_i | W)$
• 이 공식은 신경망을 훈련하기 위한 직접적인 목적 함수(Loss function)를 제공한다.

2) 자기회귀 구조 및 연쇄 법칙

• 가정: 자기회귀 모델은 데이터 $X$를 일련의 부분들($X_1, X_2, \dots, X_T$)로 분해하는 정규적인 방법이 있다고 가정한다.
• 확률의 연쇄 법칙 (Chain Rule of Probability): 어떤 결합 분포든 이 연쇄 법칙으로 분해할 수 있다 (어떠한 가정도 필요 없음).
  $\text{P}(X_1, \dots, X_T) = \text{P}(X_1) \text{P}(X_2|X_1) \text{P}(X_3|X_1, X_2) \dots \text{P}(X_T|X_1, \dots, X_{T-1})$
• 심화 내용 - 분해의 이유: 이 분해는 문제를 인수분해하여 각 부분을 모델링하기 쉽게 만든다. 만약 $T$개의 항목으로 구성된 시퀀스의 전체 결합 분포를 직접 모델링하려고 하면, 가능한 조합의 수는 $V^T$ ($V$는 어휘 크기)로 시퀀스 길이 $T$에 대해 지수적으로 증가하여 비현실적이다.
  

구현 및 적용

• RNNs (Recurrent Neural Networks): 은닉 상태(Hidden states)를 시간 순서대로 전달하여, 현재 시점의 은닉 상태가 시퀀스의 시작부터 현재 시점까지를 요약하게 함으로써 다음 부분의 확률을 예측하는 자연스러운 구조를 가진다.
• 마스크 트랜스포머 (Masked Transformers): 어텐션 행렬(Attention matrix)을 적절히 마스킹(Masking out)하여 트랜스포머의 각 출력이 시퀀스의 이전 부분(Prefix)에만 의존하도록 만들 수 있다. GPT와 같은 모델이 이러한 자기회귀적 모델링에 트랜스포머를 사용한다.
• 언어 데이터 (Text Data): 언어는 자연스럽게 1D 시퀀스이며, 토큰이 이산적(Discrete)이므로 소프트맥스 교차 엔트로피 손실(softmax cross entropy loss)을 사용하여 이산적인 확률을 모델링하는 데 매우 적합하다.
• 이미지 데이터 (Image Data):
  • 이미지는 자연적으로 1D 시퀀스가 아니며, 보통 연속적인 실수 값으로 간주되어 자기회귀 모델에 적용하기 까다롭다.
  • 나이브한 접근: 이미지를 픽셀 시퀀스로 래스터화(Rasterize)하고, 각 서브 픽셀(R, G, B 채널)을 이산적인 값(0~255)으로 처리하여 1차원 이산 시퀀스로 변환한다.
  • 한계: $1024 \times 1024$ 이미지의 경우 약 300만 개의 서브 픽셀 시퀀스가 되어, 시퀀스 길이가 너무 길고 계산 비용이 매우 비싸진다. 고해상도로 확장하기 어렵다.
  • 최신 동향: 최근에는 개별 픽셀 값 대신 이미지를 1차원 토큰(Tokens) 시퀀스로 분해하는 방식을 사용하여 이 문제가 해결되고 있다.

---

4. 변이형 오토인코더 (Variational Autoencoders, VAEs)

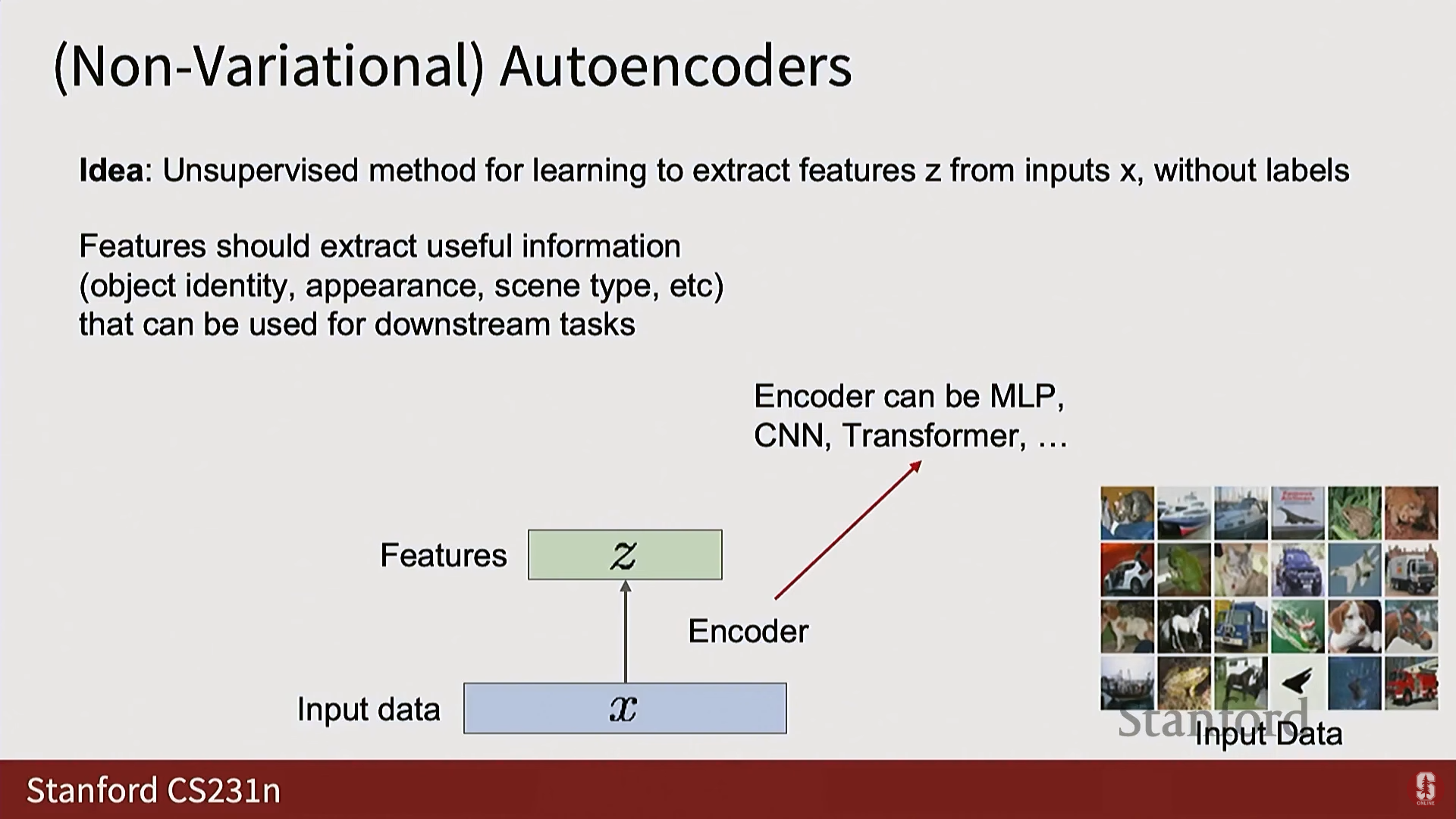
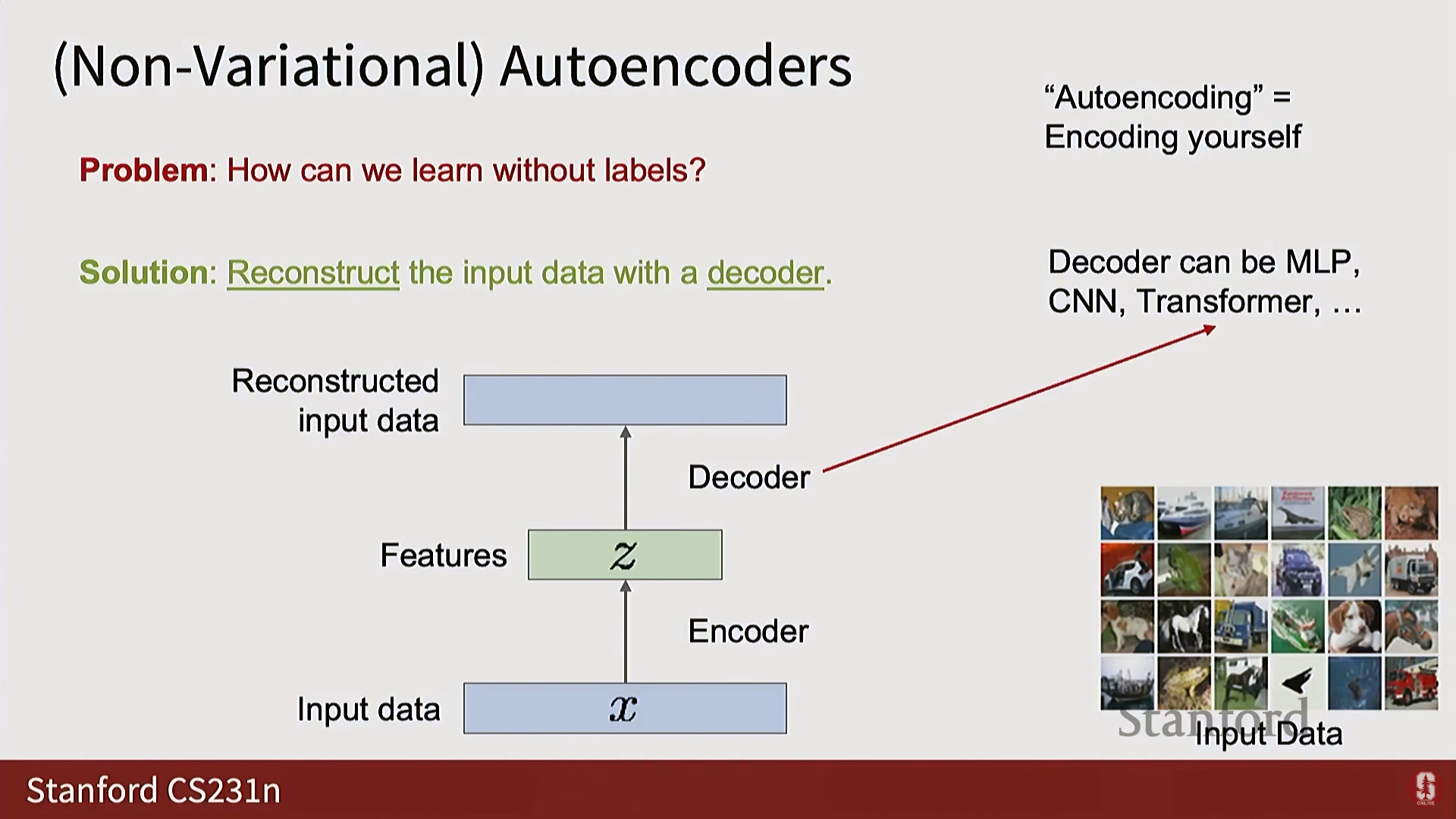
1) 오토인코더 (Autoencoders, AE)

• 비지도 특징 학습: 레이블 없이 입력 $X$로부터 특징 $Z$를 추출하도록 학습하는 비지도 방식이다.
• 구조:
  • 인코더(Encoder): $X \to Z$.
  • 디코더(Decoder): $Z \to X$.
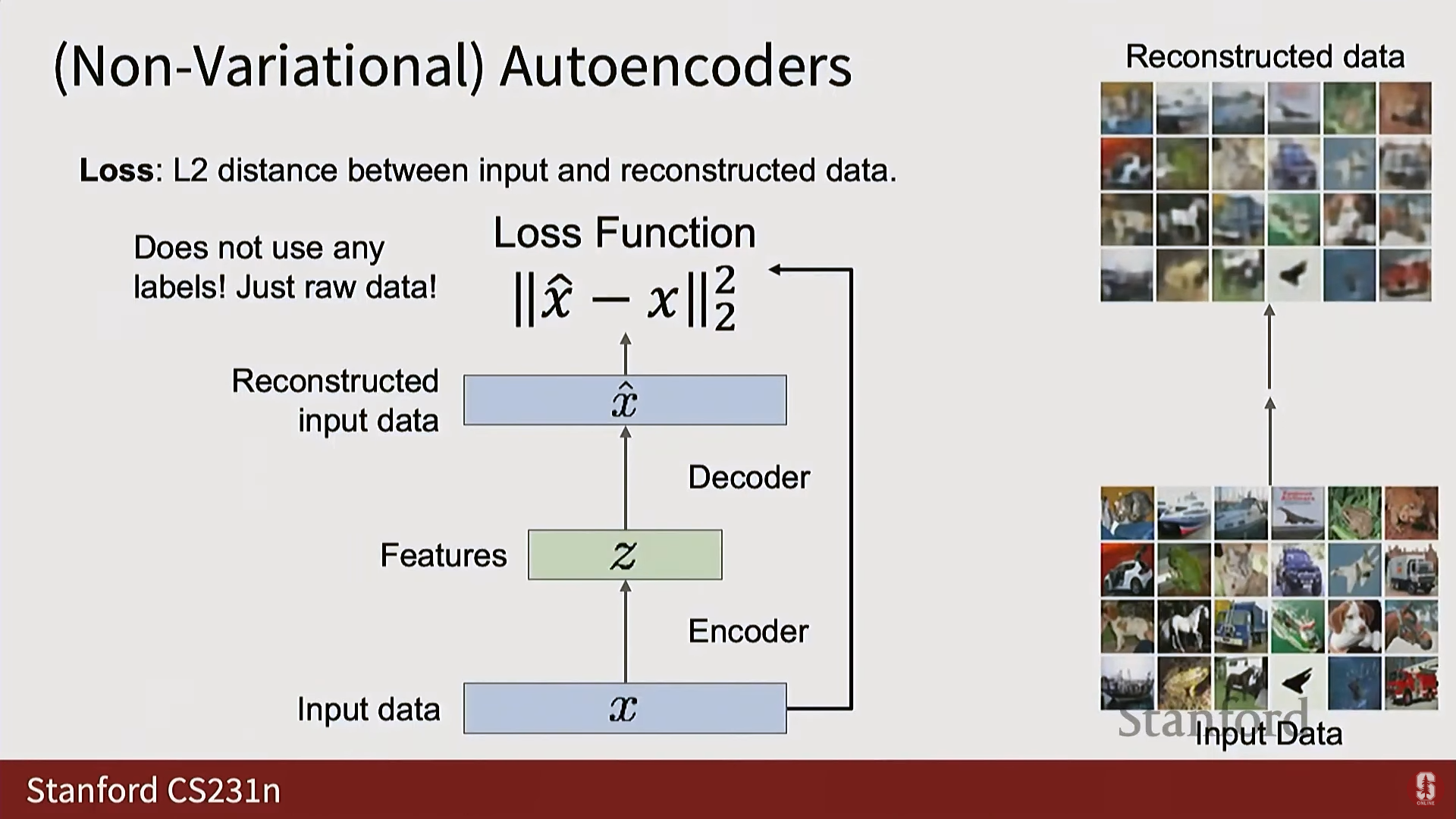
• 훈련: 모델의 출력이 입력과 일치하도록 재구성(Reconstruction) 손실을 사용한다.
• 목표: 인코더와 디코더 사이에 병목 현상(Bottleneck)을 생성하여(Z 벡터의 차원이 X보다 훨씬 작게), 모델이 항등 함수(Identity function)를 학습하되, 데이터의 비자명적인 구조(Non-trivial structure) 를 강제로 학습하도록 유도한다.
  

2) VAE의 등장: 잠재 공간에 구조 강제하기

• AE의 생성 한계: AE에서 학습된 잠재 벡터 $Z$에는 알려진 구조(Known structure)가 강제되지 않으므로, 훈련 후 $Z$ 공간에서 새로운 샘플을 생성하기 어렵다.
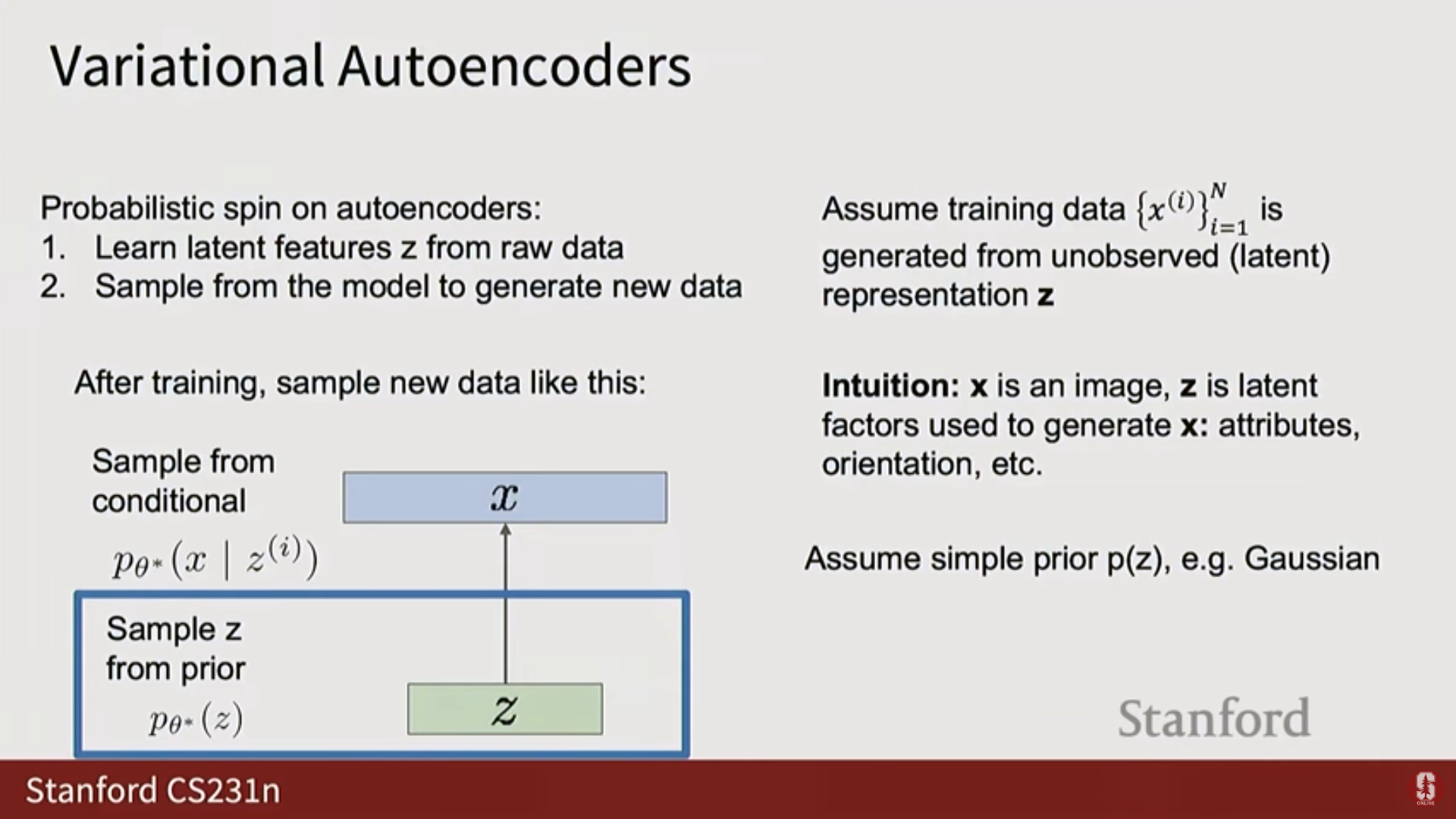
• VAE의 목표: 잠재 벡터 $Z$가 가우시안 분포(Gaussian distribution)와 같은 알려진 확률적 구조를 따르도록 강제하여, 훈련 후 이 분포에서 샘플링하고 디코더에 통과시켜 새로운 샘플을 생성할 수 있게 한다.
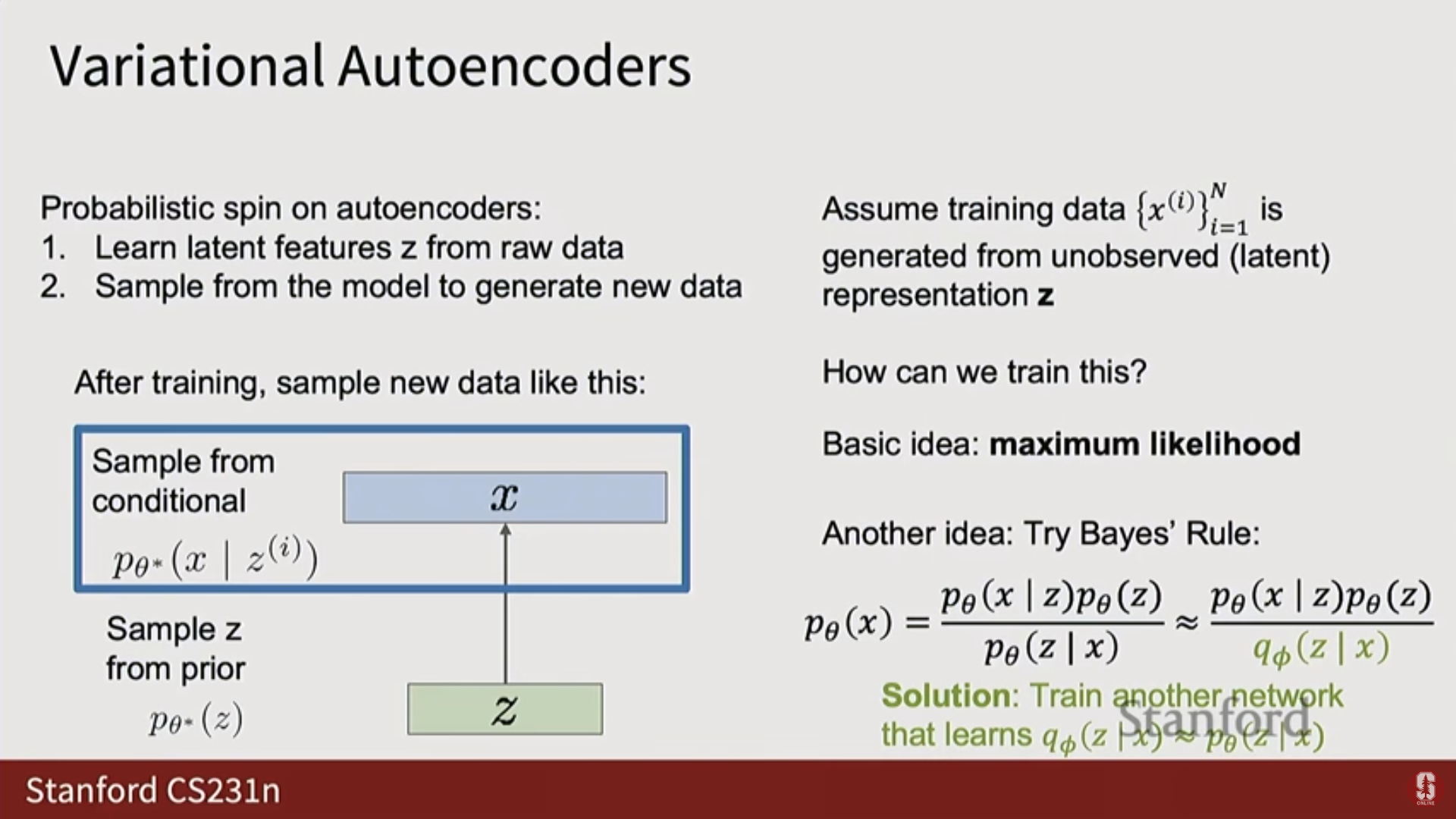
• VAE 가정:
  1. 데이터 $X$는 관찰할 수 없는 잠재 벡터 $Z$로부터 생성되었다고 가정한다.
  2. 잠재 벡터 $Z$는 단순한 사전 분포(Simple prior), 보통 단위 가우시안 분포(Unit Gaussian distribution) $P(Z)$를 따른다고 가정한다.

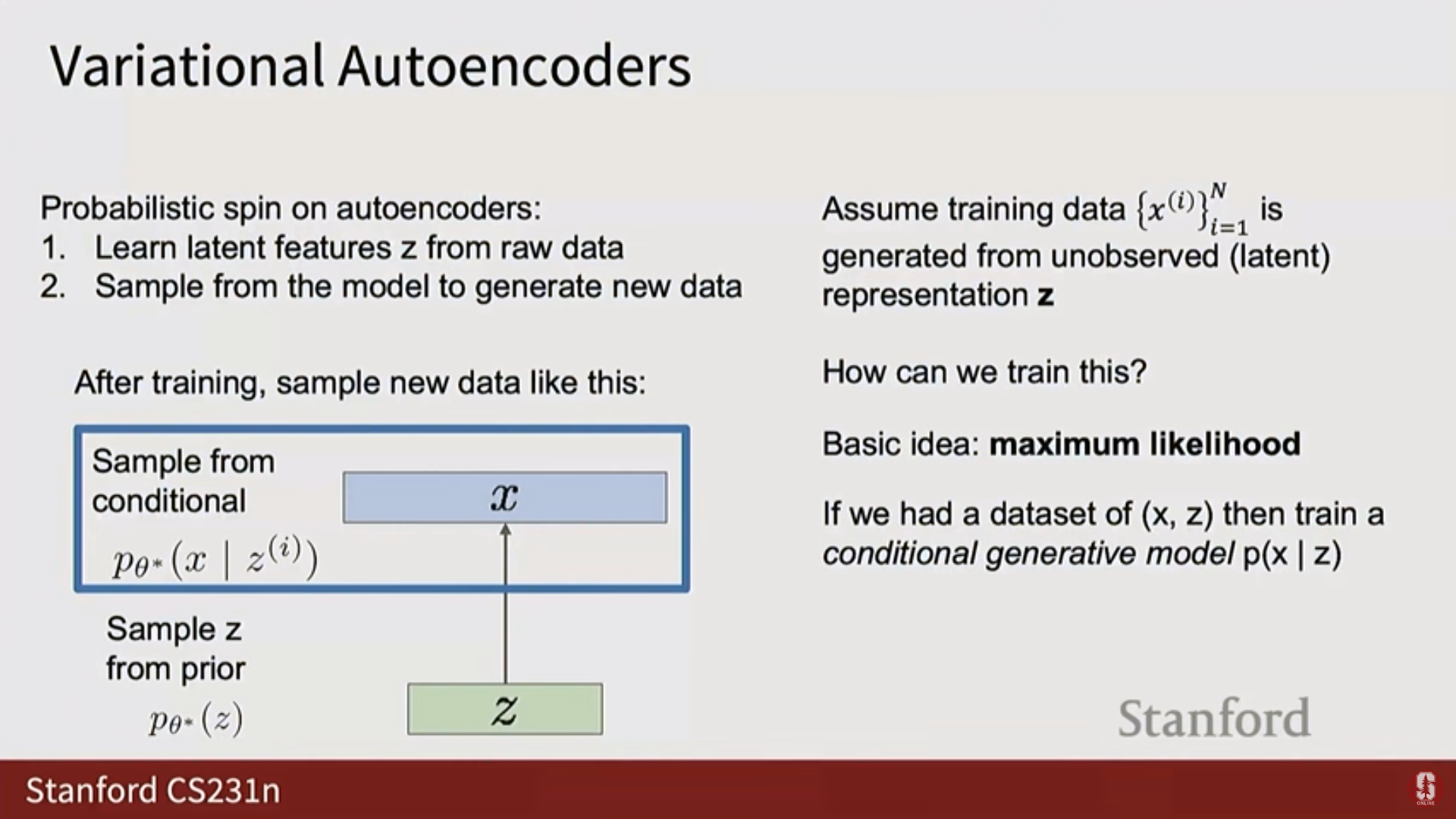
3) VAE의 수학적 기반: ELBO (Evidence Lower Bound)

(1) 최대 우도의 난제

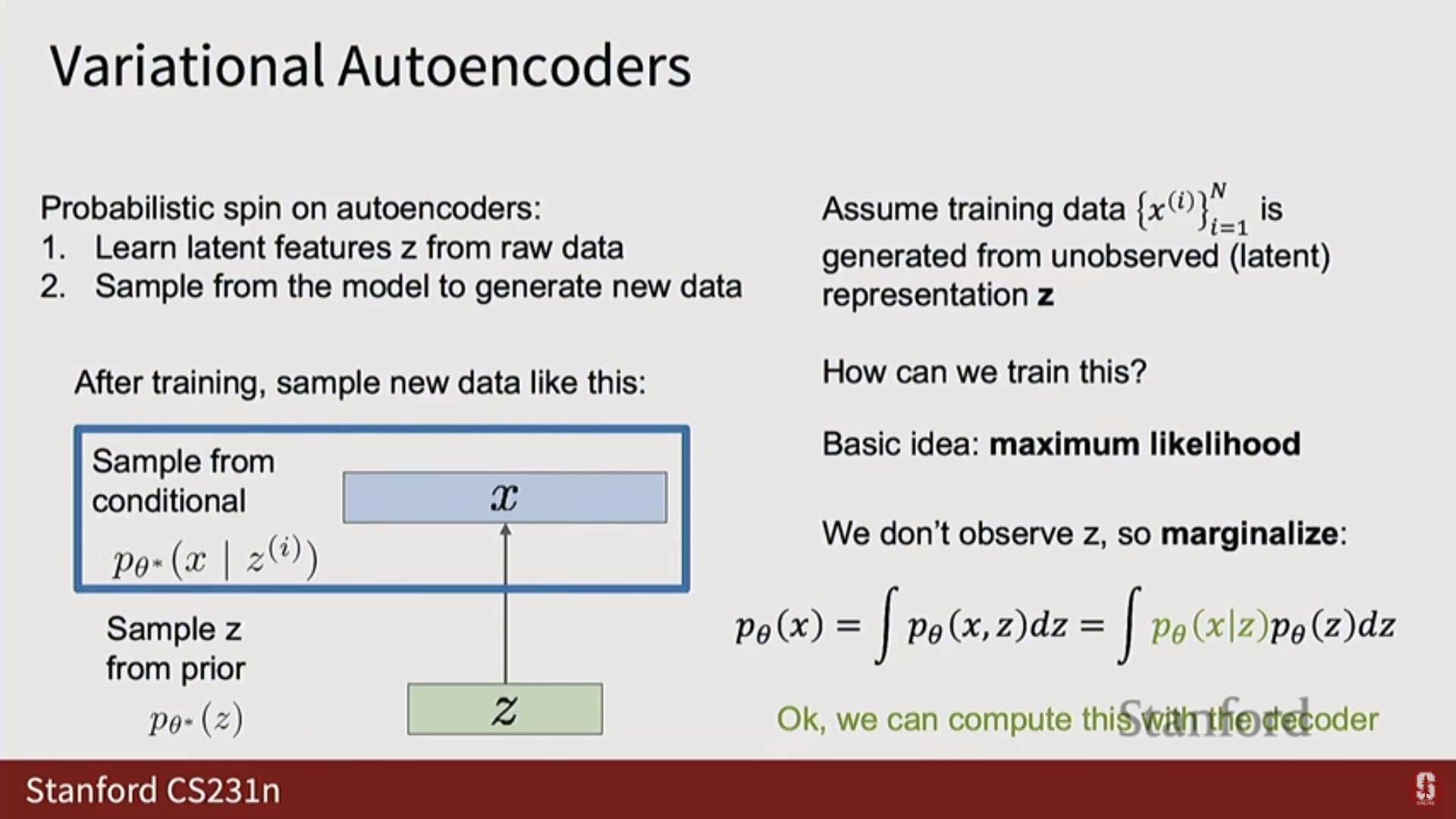
• VAE 역시 최대 우도 $\log P(X)$를 최대화하고자 한다.
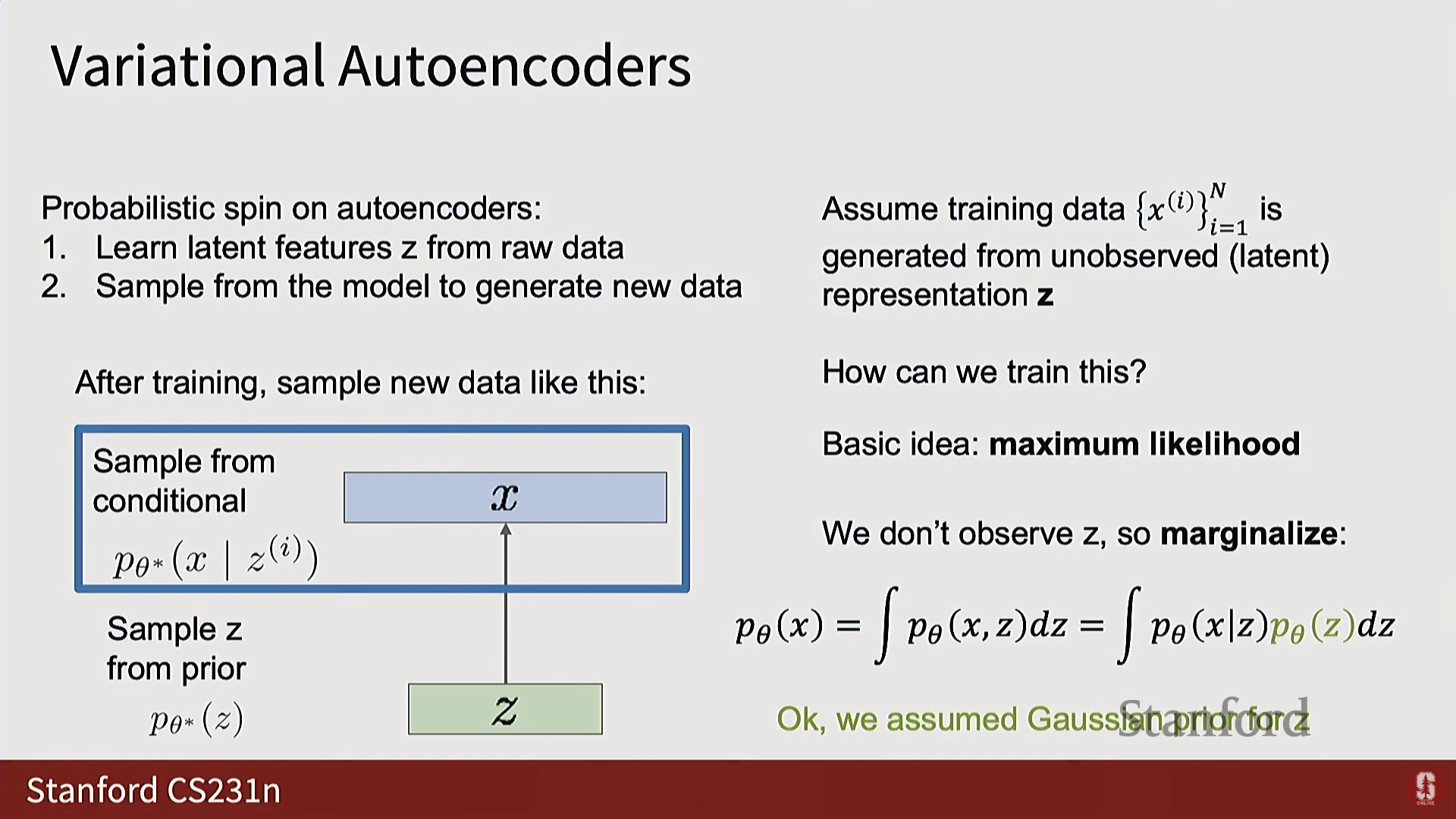
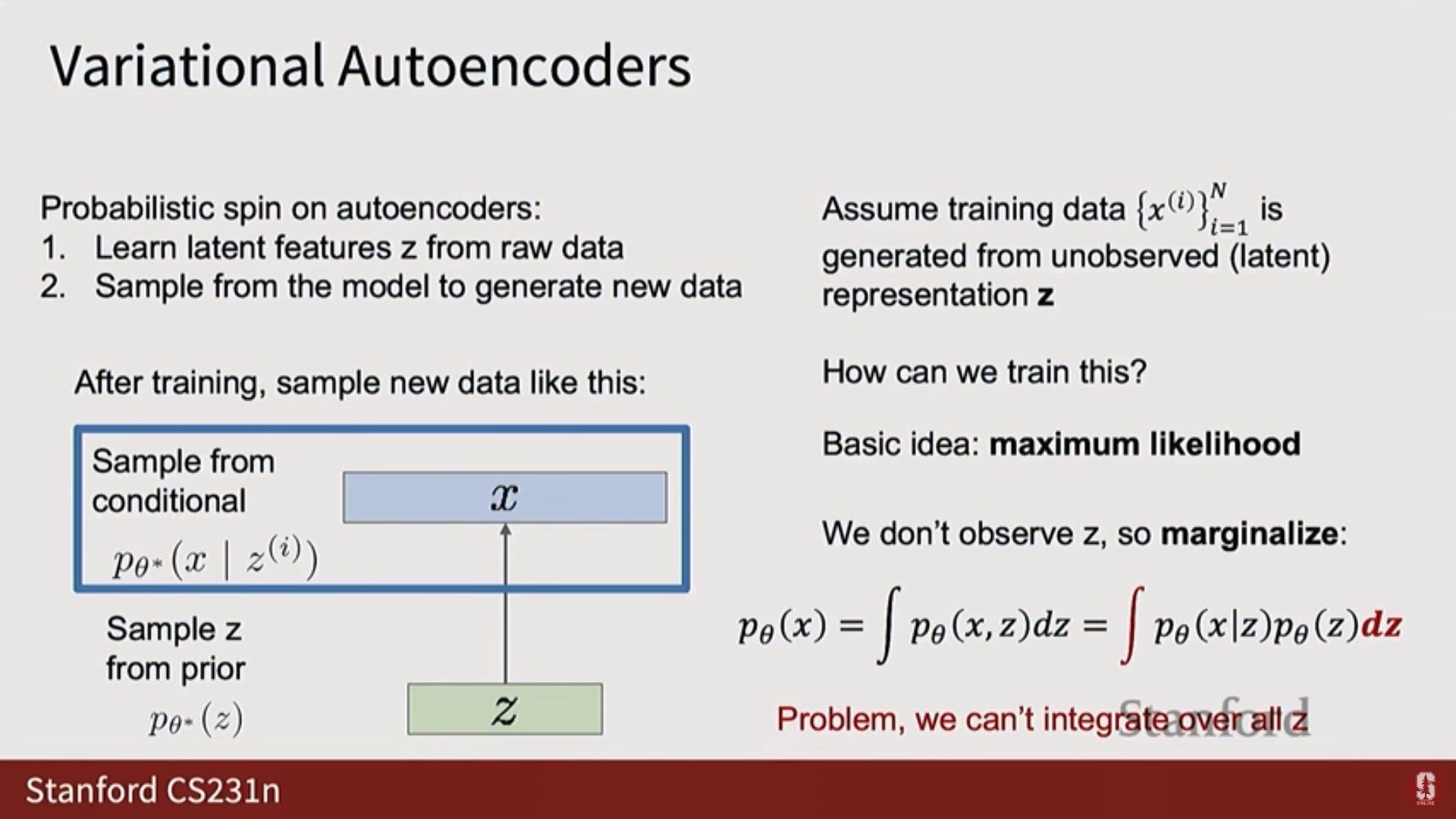
• $\log P(X)$를 구하기 위해 $P(X)$를 주변화(Marginalize)하여 표현하면 다음과 같다:
  $\text{P}(X) = \int \text{P}(X|Z) \text{P}(Z) dZ$
• 문제점: $P(X|Z)$가 신경망으로 모델링되는 복잡한 함수이기 때문에, 잠재 공간 $Z$에 대한 이 적분(Integral)을 분석적으로 또는 정확히 계산하는 것이 불가능하다.
  

(2) 변이적 접근 (Variational Approach)

• 베이즈 정리($P(X) = P(X|Z)P(Z) / P(Z|X)$)를 사용해도 사후 분포(Posterior) $P(Z|X)$를 계산하기 위한 적분 때문에 여전히 막힌다.
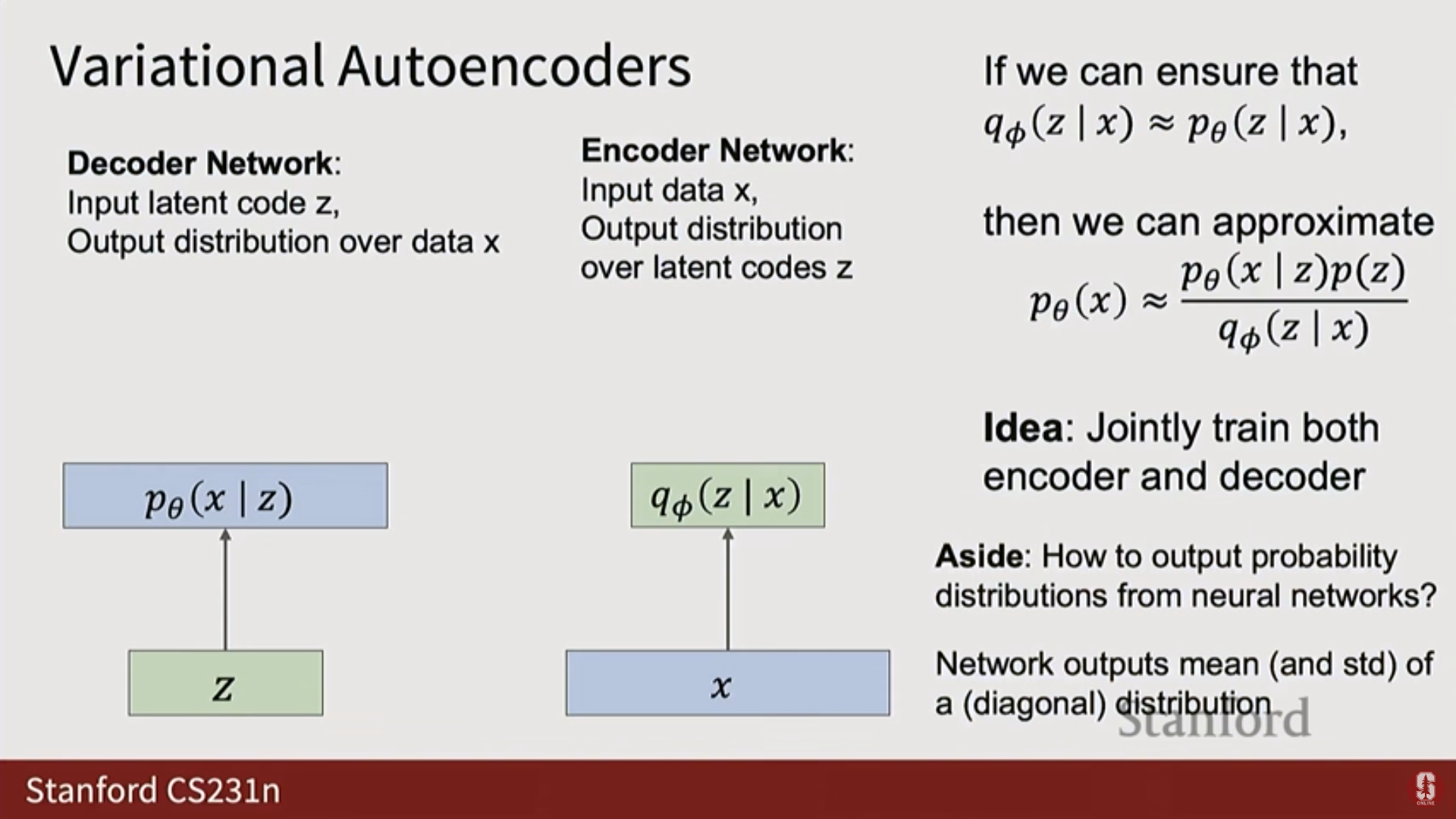
• VAE의 핵심 트릭: 계산 불가능한 $P(Z|X)$ (참 사후 분포)를 근사하기 위해, 새로운 신경망인 인코더 $Q(Z|X)$ (변이 분포, Variational distribution) 를 도입한다.
• 공동 훈련: 디코더 $P(X|Z)$와 인코더 $Q(Z|X)$라는 두 개의 별도 신경망을 동시에 훈련한다.
  

(3) 신경망 출력 분포

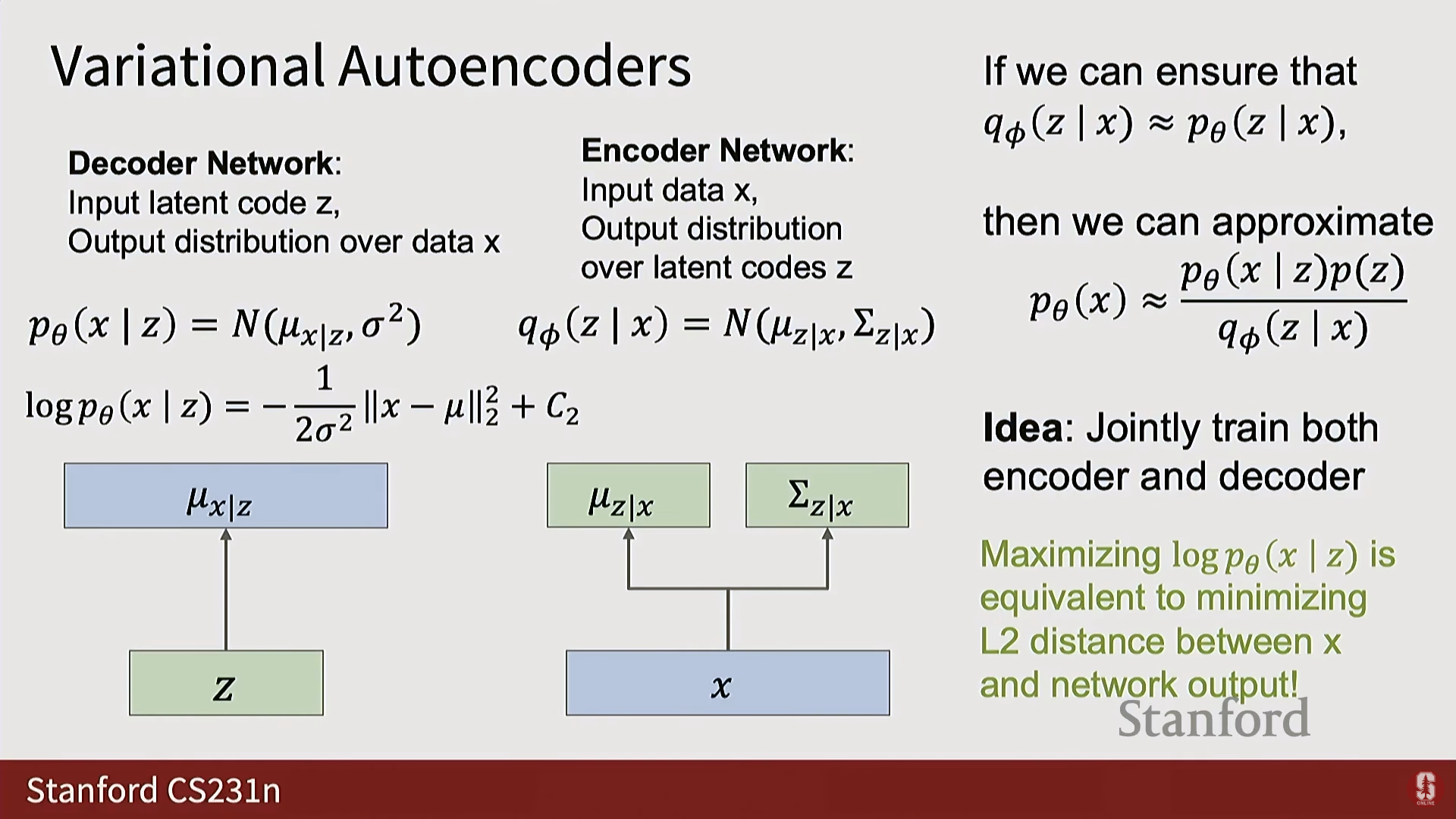
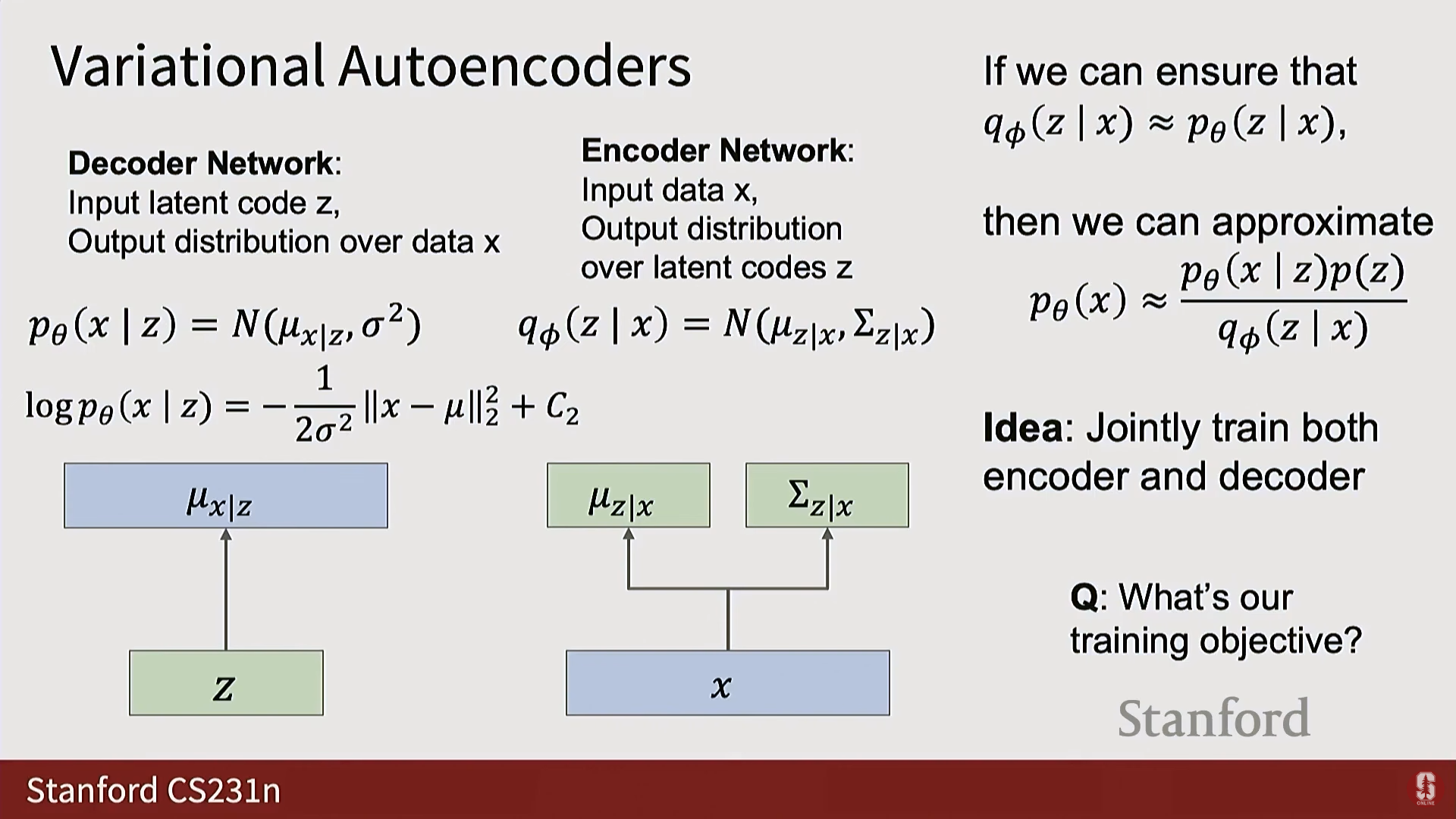
• VAE는 확률 분포를 출력하도록 신경망을 훈련시키기 위해, 모든 분포를 정규 분포(Normal distribution) 로 가정하고, 신경망이 이 정규 분포의 매개변수($\mu, \sigma$) 를 출력하도록 만든다.
  • 디코더 $P(X|Z)$: 입력 $Z$를 받아 $X$에 대한 정규 분포의 평균($\mu_X$)을 출력한다. 분산($\sigma^2$)은 고정된 값으로 가정하는 경우가 많다.
  • 인코더 $Q(Z|X)$: 입력 $X$를 받아 잠재 공간 $Z$에 대한 정규 분포의 평균($\mu_Z$)과 공분산의 대각선($\sigma_Z$)을 출력한다. (대각선 구조를 가정하여 모델링해야 할 매개변수의 수를 줄인다).

(4) ELBO 유도 및 목적 함수 (수학적 내용)

• 최대화하려는 $\log P(X)$에 $Q(Z|X)$를 곱하고 나누는 등의 수학적 조작(로그 및 기대값 적용)을 통해 $\log P(X)$를 세 개의 항으로 분해한다.
• 이 과정에서 $\log P(X)$가 다음과 같이 재구성 항(Reconstruction Term), 사전 분포 항(Prior Term), 그리고 KL 발산 항으로 나뉨을 알 수 있다:
  $\log P(X) = \mathbb{E}_{Z \sim Q}[\log P(X|Z)] - \text{KL}(Q(Z|X) || P(Z)) + \text{KL}(Q(Z|X) || P(Z|X))$
• 최종 목적 함수:
  • 마지막 항 $\text{KL}(Q(Z|X) || P(Z|X))$은 참 사후 분포 $P(Z|X)$가 포함되어 있어 계산이 불가능하다.
  • KL 발산은 항상 0보다 크거나 같다 ($\text{KL} \ge 0$)는 잘 알려진 속성을 이용하여 이 항을 버리면, $\log P(X)$의 하한(Lower Bound) 을 얻게 된다.
    $\log P(X) \ge \underbrace{\mathbb{E}_{Z \sim Q}[\log P(X|Z)]}_{\text{재구성 손실 (Reconstruction)}} - \underbrace{\text{KL}(Q(Z|X) || P(Z))}_{\text{사전 분포 손실 (Prior Matching)}}$
• 이 하한을 변이적 하한(Variational Lower Bound) 또는 증거 하한 (Evidence Lower Bound, ELBO) 이라 부르며, VAE는 ELBO를 최대화하도록 훈련된다.
  

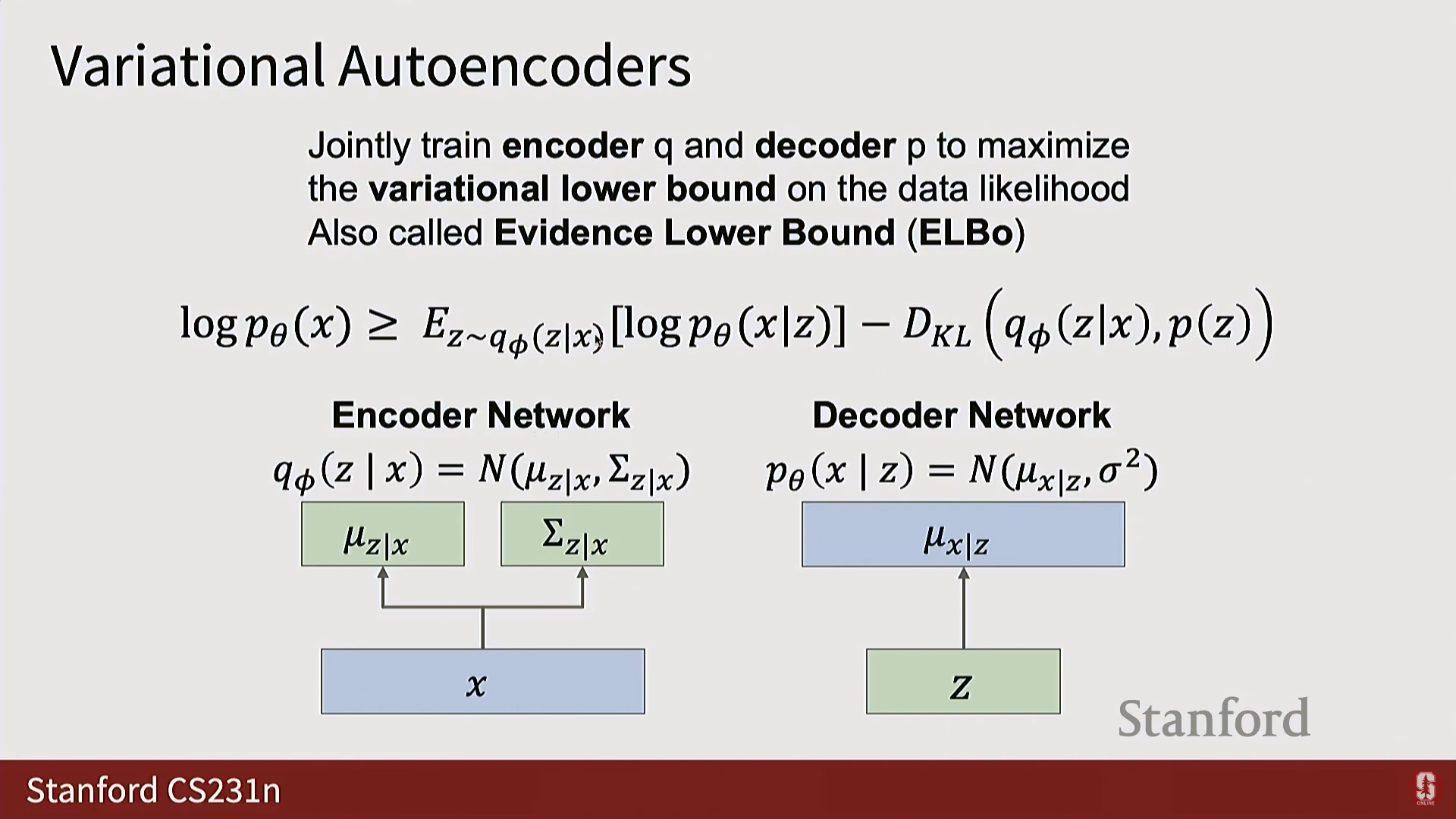
(5) ELBO 각 항의 의미

1. 재구성 항 (Reconstruction Term, $\mathbb{E}_{Z \sim Q}[\log P(X|Z)]$):
   • $X$를 인코더 $Q$에 통과시켜 $Z$ 분포를 얻고, 이 분포에서 샘플링한 $Z$를 디코더 $P$에 통과시켜 $X$를 얼마나 잘 복원하는지를 측정한다.
2. 사전 분포 항 (Prior Matching Term, $\text{KL}(Q(Z|X) || P(Z))$):
   • 인코더가 예측한 잠재 공간 분포 $Q(Z|X)$가 우리가 사전에 정의한 단순한 가우시안 사전 분포 $P(Z)$와 얼마나 일치하는지 측정한다.
   • 이 항은 $Q$의 평균($\mu_Z$)이 0이 되도록, 그리고 분산($\sigma_Z$)이 모두 1이 되도록 장려한다.

(6) 심화 내용 - 손실 간의 경쟁 및 특성

• VAE 훈련에서 재구성 손실과 사전 분포 손실은 서로 경쟁한다.
  • 재구성 손실: 완벽한 재구성을 위해 $\sigma_Z$가 0이 되고 각 데이터 $X$마다 $\mu_Z$가 고유하고 분리된 벡터가 되기를 원한다.
  • 사전 분포 손실: $Z$가 단위 가우시안을 따르도록 $\sigma_Z$가 1이 되고 $\mu_Z$가 0이 되기를 원한다.
• VAE는 이 두 손실의 상충 관계(Trade-off) 속에서 균형점(Equilibrium)을 찾도록 훈련된다.
• 잠재 공간의 특성: 잠재 공간 $Z$가 가우시안 분포로 강제되기 때문에, $Z$의 차원 간에 통계적 독립성(Statistical independence)이 있으며, 이는 잠재 차원을 독립적으로 변화시켜 데이터의 유용하거나 해석 가능한 특성(예: 필기체 숫자의 모양 변화)을 부드럽게 보간(Smoothly morph)할 수 있게 한다.
  

---

5. Q&A 세션

1) 생성 모델의 입출력 구성 (Generative Model Inputs/Outputs)

• 질문: 비조건부 생성 모델 $P(X)$를 어떻게 매개변수화(parameterize)하는가?
• 답변: 모델의 입력과 출력이 정확히 무엇이 될지는 모델의 형식(Formulation)에 따라 크게 달라진다. 이는 다음 슬라이드의 분류와 함께 구체적으로 논의될 것이다.

2) 간접 암시적 모델의 샘플링 (Indirect Implicit Sampling)

• 질문: 간접(Iterative) 방식을 블랙박스(Blackbox)로 보고 직접 샘플링 방식으로 취급할 수 있는가?
• 답변: 원칙적으로는 가능하지만, 실제로는 불가능하다. 확산 모델(Diffusion models)과 같은 간접 방식은 정확한 샘플을 얻기 위해 무한한 수의 스텝(Infinite number of steps)을 필요로 하며, 따라서 우리는 항상 유한한 스텝으로 근사(Approximate)할 수밖에 없다.

3) 근사 밀도 vs. 암시적 밀도 (Approximate vs. Implicit Density)

• 질문: 근사 밀도와 암시적 밀도 $P(X)$로부터 직접 샘플링하는 것의 차이점은 무엇인가?
• 답변: 근사 밀도 방식(예: VAE)에서는 $P(X)$ 값의 근삿값 또는 하한을 계산하여 얻을 수 있다. 반면, 암시적 방식(예: GAN)에서는 밀도 값을 전혀 계산할 수 없지만, 반복적(Iterative)으로라도 샘플을 생성할 수는 있다.

4) 로그 트릭 적용 (Applying the Log Trick)

• 질문: 로그 트릭(Log trick)을 적용하여 (자기회귀 모델에서) 지수적 증가 문제를 완화할 수 있는가?
• 답변: 실제로 확률 밀도 값 자체를 모델링하는 경우는 거의 없고, 수치적 안정성을 위해 거의 모든 계산을 로그 확률(Log probabilities) 공간에서 수행한다.

5) 자기회귀 모델의 시퀀스 분해 이유 (Why Sequence Decomposition in Auto-regressive Models)

• 질문: 자기회귀 모델에서 데이터를 시퀀스로 분해하는 동기는 무엇인가?
• 답변: 문제를 인수분해하여 각 부분을 모델링하기 쉽게 만들기 위함이다. 시퀀스의 길이를 $T$, 어휘 크기를 $V$라고 할 때, 전체 결합 분포를 직접 모델링하면 필요한 이산 확률 분포의 엔트리 수가 $V^T$로 시퀀스 길이에 대해 지수적으로 증가하여 비현실적이 된다.

6) 자기회귀 모델에서 $P(X)$ 복원 (Recovering $P(X)$ in Auto-regressive Models)

• 질문: 자기회귀 모델(예: 트랜스포머)이 $P(X)$를 정확히 생성하는가?
• 답변: 그렇다. 트랜스포머는 시퀀스의 모든 지점에서 이전 토큰에 조건화된 다음 토큰에 대한 확률 분포를 출력한다. 입력 시퀀스가 주어지면, 시퀀스 전체에 걸쳐 해당 토큰의 예측 확률을 모두 곱하여 정확한 밀도 값 $P(X)$를 복원할 수 있다.

7) 픽셀 시프팅 비변성 (Pixel Shifting Non-invariance)

• 질문: 픽셀 시프팅(Pixel shifting)과 관련된 이상한 비변성(non-invariance) 구조가 있는가?
• 답변: 그것은 손실 함수 수준에서 설명되는 것이 아니라, 신경망 구축에 선택한 아키텍처(Architecture) 의 속성에 더 가깝다. 아키텍처 자체에 변성(Equivariance) 또는 불변성(Invariance) 속성을 구축하려고 시도할 수는 있다.