1. 개요
생성 모델링 (Generative Modeling) 개요
- 지난 시간에 생성 모델에 대해 논의를 시작했다.
- 확률론적 모델은 판별 모델(discriminative models)과 생성 모델(generative models)로 나뉘는데, 이는 우리가 무엇을 예측하려고 하는지, 무엇을 조건화하는지, 그리고 무엇에 대해 정규화하는지에 따라 구분된다.
(1) 판별 모델 vs. 생성 모델
- 판별 모델 (Discriminative Models): 데이터 가 주어졌을 때 레이블 를 예측하려고 한다 ( 모델링).
- 생성 모델 (Generative Models): 데이터 자체의 확률 분포를 학습하려고 한다 ( 모델링).
- 조건부 생성 모델 (Conditional Generative Models): 사용자 입력 (또는 레이블)에 조건화된 데이터 를 모델링한다 ( 모델링).
- 이 모델들은 확률 분포의 정규화 제약 조건으로 인해 확률 질량(probability mass)을 놓고 경쟁해야 한다는 점에서 차이가 발생한다.
(2) 생성 모델의 분류 및 지난 시간 복습
- 생성 모델링 분야는 오랫동안 연구되어 왔으며 다양한 방법론들이 존재한다.
- 지난 시간에는 생성 모델의 분류 체계(taxonomy) 중 명시적 밀도 모델(Explicit Density Models)에 대해 논의했다.
- 명시적 밀도 모델은 모델이 라는 특정 양을 출력하는 모델이다.
- 다루기 쉬운 밀도 모델 (Tractable Density Models): 정확한 를 출력한다. 예시로 자기회귀 모델 (Auto Regressive Models)이 있다.
- 자기회귀 모델은 이미지나 데이터를 시퀀스로 분할하고, 픽셀 값이나 서브 픽셀 값을 0에서 255 사이의 8비트 정수 시퀀스로 취급하여 이산적인 시퀀스 모델(일반적으로 RNN 또는 Transformer)을 사용하여 모델링한다.
- 근사 밀도 모델 (Approximate Density Models): 의 근사 버전을 출력한다. 예시로 변이형 자기부호화기 (Variational Auto-Encoders, VAEs)가 있다.
- VAE는 정확한 밀도가 아닌 밀도의 하한(lower bound)을 계산하는 명시적 밀도 모델이다.
- VAE는 데이터 를 입력하고 잠재 코드 에 대한 분포를 출력하는 인코더 네트워크와, 잠재 코드 를 입력하고 예측 데이터 를 출력하는 디코더 네트워크를 함께 훈련하여 우도 함수(likelihood function)의 변이적 하한(variational lower bound)을 최대화하도록 학습한다.
- 다루기 쉬운 밀도 모델 (Tractable Density Models): 정확한 를 출력한다. 예시로 자기회귀 모델 (Auto Regressive Models)이 있다.
- 명시적 밀도 모델은 모델이 라는 특정 양을 출력하는 모델이다.
(3) 잠재적 밀도 모델 (Implicit Density Models) 소개
- 오늘 강의에서는 생성 모델 분류 체계의 나머지 절반인 잠재적 밀도 모델 (Implicit Density Models)에 대해 탐구한다.
- 이 모델들에서는 더 이상 실제 밀도 값 에 접근할 수 없다.
- 하지만 이러한 모델들은 확률 분포를 잠재적으로(implicitly) 모델링하며, 특정 데이터 에 대한 밀도 값 를 계산할 수 없더라도 학습된 기본 분포로부터 샘플을 추출할 수 있다.
2. GAN (Generative Adversarial Networks): 잠재적 밀도 모델
1) GAN의 기본 개념 및 VAE/자기회귀 모델과의 차이

- 오늘 탐구할 첫 번째 잠재적 밀도 모델은 적대적 생성 네트워크(Generative Adversarial Networks, GANs)이다.
- GAN은 VAE나 자기회귀 모델과는 다르게 를 직접 모델링하는 것을 포기한다.
- 자기회귀 모델과 VAE가 최대 우도(maximum likelihood)를 목표 함수로 사용하여 를 모델링하는 것과 달리, GAN은 를 명시적으로 모델링하지 않으면서도 샘플링을 가능하게 한다.
GAN의 목표 및 데이터 분포
- GAN 훈련의 목표는 모델이 학습한 분포 가 실제 데이터 분포 와 가능한 한 가깝게 일치하도록 강제하는 것이다.
- 는 우리가 관찰하는 데이터 샘플을 생성하는 우주의 실제 분포이며, 매우 복잡하고 물리, 역사, 사회정치적 제약 등 복잡한 요소를 포함한다.
- 우리의 목표는 와 일치하는 근사 모델을 학습하여, 관찰된 데이터와 유사한 새로운 샘플을 생성하는 것이다.
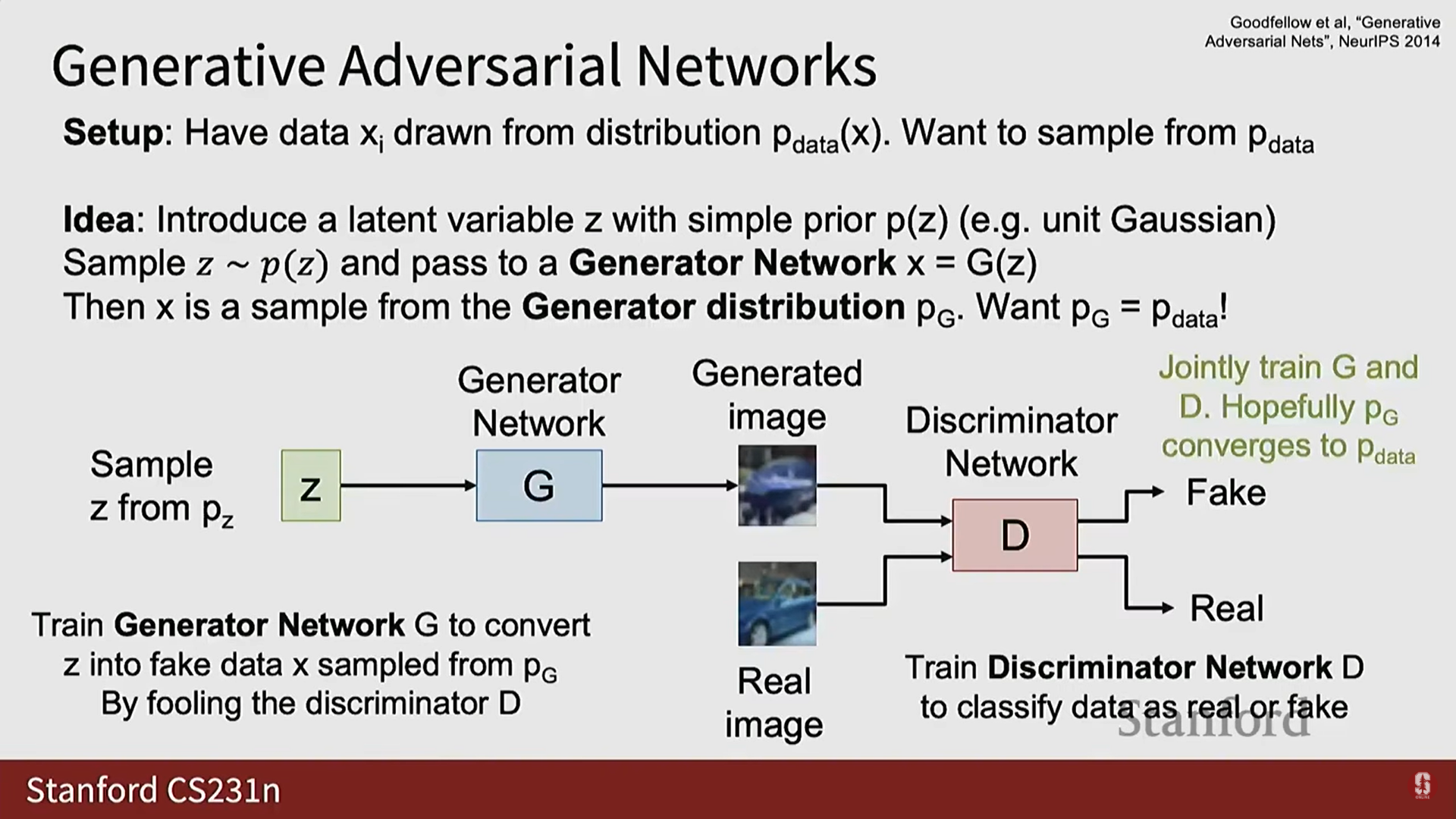
2) GAN의 구조: 생성자 G와 판별자 D
- GAN은 잠재 변수 를 도입한다. 이는 VAE에서 본 잠재 변수와 유사하다.
- 잠재 변수 : 우리가 직접 설정하고 제어하는 알려진 사전 분포(prior distribution) 를 따른다 (일반적으로 단위 가우시안 또는 균일 분포).
- 생성자 네트워크 :
- 에 따라 를 샘플링하고, 이 를 입력받아 데이터 샘플 를 출력한다 ().
- 는 생성자 분포 로부터의 샘플이 된다.
- 는 알려진 분포 로부터의 샘플을 데이터 분포의 샘플로 변환하도록 훈련된다.
- 가 와 일치하게 되면, 를 샘플링하고 를 통과시켜 와 매우 유사한 새로운 데이터 샘플을 얻을 수 있다.
- 판별자 네트워크 :
- 가 와 일치하도록 강제하기 위해 도입된 또 다른 신경망이다.
- 이미지를 입력받아 해당 이미지가 가짜(fake)인지 진짜(real)인지를 분류하는 임무를 맡는다.
- 적대적 학습 (Adversarial Training):
- 생성자 는 판별자 를 속이려고 훈련된다.
- 판별자 는 진짜 데이터와 가짜 데이터를 정확하게 판별하도록 분류 모델로 훈련된다.
- 이 두 네트워크가 서로 경쟁하면서 (싸우면서), 이상적으로는 판별자가 진짜 데이터와 가짜 데이터의 특징을 구별하는 데 매우 능숙해지고, 생성자는 판별자를 속이기 위해 참 데이터와 점점 더 유사한 샘플을 생성해야 한다.
- 피드백: 생성자는 생성된 이미지를 통해 판별자로부터 그래디언트 형태의 피드백을 받으며 학습한다. 이 그래디언트는 판별자로부터 생성된 이미지를 거쳐 생성자로 역전파된다.
3) GAN의 수학적 형식화: Minimax Game
- GAN은 최소-최대 게임 (minimax game)을 통해 생성자 와 판별자 를 동시에 훈련한다.
- 판별자 는 데이터 를 입력받아 해당 데이터가 진짜일 확률을 출력하는 함수이다 ().
- : 판별자가 를 가짜로 분류했다.
- : 판별자가 를 진짜로 분류했다.
(1) GAN 목적 함수 (Minimax Value Function)
GAN의 목적 함수 는 다음과 같다:
- 이 수식에서 판별자 는 를 최대화(maximize)하려고 하고, 생성자 는 를 최소화(minimize)하려고 한다.
(2) 판별자의 관점 (Maximize D)
- 는 를 최대화하려고 한다.
- 첫 번째 항 ():
- 분포에서 데이터 를 샘플링할 때, 가 1에 가깝도록 (즉, 진짜 데이터를 진짜로 분류하도록) 를 최대화한다.
- 두 번째 항 ():
- 분포에서 잠재 변수 를 샘플링하고 를 거쳐 생성된 가짜 데이터 를 판별자에 입력한다.
- 가 0에 가깝도록 (즉, 가짜 데이터를 가짜로 분류하도록) 를 최대화한다.

(3) 생성자의 관점 (Minimize G)
- 는 를 최소화하려고 한다.
- 첫 번째 항은 에 의존하지 않으므로, 는 두 번째 항에만 관심을 갖는다.
- 두 번째 항 ():
- 는 생성된 샘플에 대해 가 1에 가깝도록 (즉, 판별자를 속여 가짜 데이터를 진짜로 분류하도록) 이 항을 최소화하기를 원한다.

- 는 생성된 샘플에 대해 가 1에 가깝도록 (즉, 판별자를 속여 가짜 데이터를 진짜로 분류하도록) 이 항을 최소화하기를 원한다.
4) GAN 훈련 및 불안정성
(1) 최적화 과정
- 훈련은 경사 하강법 루프를 번갈아 수행하며 진행된다.
- 판별자 업데이트: 의 가중치에 대해 를 최대화하기 위해 경사 상승(gradient ascent) 단계를 수행한다 (최적화 방향: ).
- 생성자 업데이트: 의 가중치에 대해 를 최소화하기 위해 경사 하강(gradient descent) 단계를 수행한다 (최적화 방향: ).

(2) 훈련의 어려움 및 한계 (심화)
- 는 손실 함수가 아니다: 의 절대값은 생성자와 판별자가 문제를 얼마나 잘 해결하고 있는지 또는 가 와 얼마나 잘 일치하는지에 대해 아무것도 알려주지 않는다.
- 가 정말 나쁘면 가 낮은 값을 쉽게 얻을 수 있고, 가 정말 좋으면 도 정말 좋아야 한다. 와 의 다른 설정이 에 대해 동일한 값을 초래할 수 있다.
- 근본적인 불안정성: GAN은 본질적으로 불안정한 최적화 문제를 가진다. 같은 양을 다른 매개변수 집합에 대해 동시에 최대화하고 최소화하려고 시도하기 때문이다.
- 훈련 초기 문제 (Vanishing Gradient):
- 훈련 초기에 는 완전히 무작위의 노이즈를 생성하며, 는 진짜 이미지와 가짜 이미지(노이즈)를 매우 쉽게 구별한다.
- 가 가짜 샘플을 '가짜'로 분류하는 데 매우 능숙해지면, 생성자 의 관점에서 손실 함수( )는 가 최적화하려는 지점에서 평평해져서(flat) 그래디언트가 사라지는(vanishing gradient) 문제가 발생한다. 이로 인해 는 학습하는 데 어려움을 겪는다.
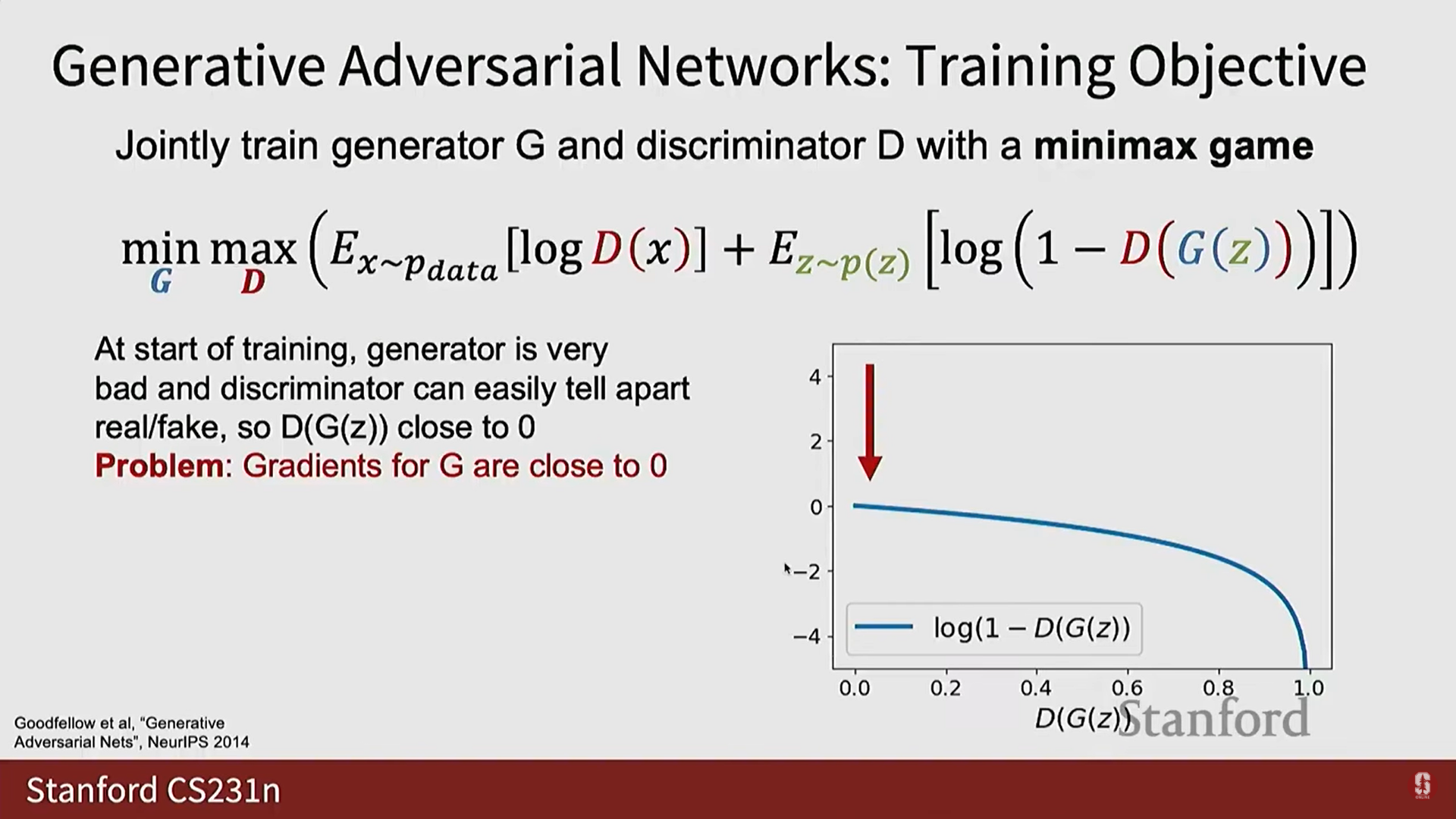

(3) 생성자를 위한 수정된 손실 함수 (Modified Loss)
- 이러한 초기 훈련 문제를 해결하기 위한 '꼼수'가 있다.
- 를 최소화하는 대신, 를 최소화하도록 수정할 수 있다.
- 이 수정된 손실 함수는 훈련 초기에 생성자에게 더 나은 그래디언트를 제공하며, 실제로 GAN을 처음부터 훈련할 때 이 수정된 손실을 사용하는 것이 매우 중요하다. (이 경우 생성자가 계산하는 와 판별자가 계산하는 는 엄밀히 같지 않다).
(4) GAN의 이론적 정당성 및 실제적 한계
- GAN의 목적 함수는 이론적으로 정당성이 있다.
- 이는 내재된 최적화 문제( 후 )이므로, 수학적으로 최적의 판별자 를 도출할 수 있다.
- 최적의 판별자를 목적 함수에 대입한 후, 외부 목표 함수를 최소화할 때, 일 때만 최소값이 발생함을 보일 수 있다.
- 주의 사항: 이 이론적 결과는 다음을 가정한다:
- 와 의 잠재적 용량이 무한대여서 어떤 함수든 원칙적으로 표현할 수 있다. (실제로는 불가능).
- 경사 하강/상승을 통해 이 최적점에 도달할 수 있는지, 유한한 데이터 샘플로 도달할 수 있는지에 대해서는 아무것도 알려주지 않는다.

(5) GAN의 발전 및 특징 (심화)
-
초기 GAN은 신경망으로 매개변수화되었으며, 주로 CNN을 사용했다.
-
DC GAN: 처음으로 비자명(non-trivial)한 결과를 보여준 GAN으로, 5계층 콘볼루션 아키텍처를 가졌다.
- DC GAN의 첫 번째 저자인 Alec Radford는 이후 GPT-1 및 GPT-2를 포함한 OpenAI의 중요한 작업을 수행하며 이미지 생성 모델링에서 이산 텍스트 생성 모델링으로 넘어갔다.

- DC GAN의 첫 번째 저자인 Alec Radford는 이후 GPT-1 및 GPT-2를 포함한 OpenAI의 중요한 작업을 수행하며 이미지 생성 모델링에서 이산 텍스트 생성 모델링으로 넘어갔다.
-
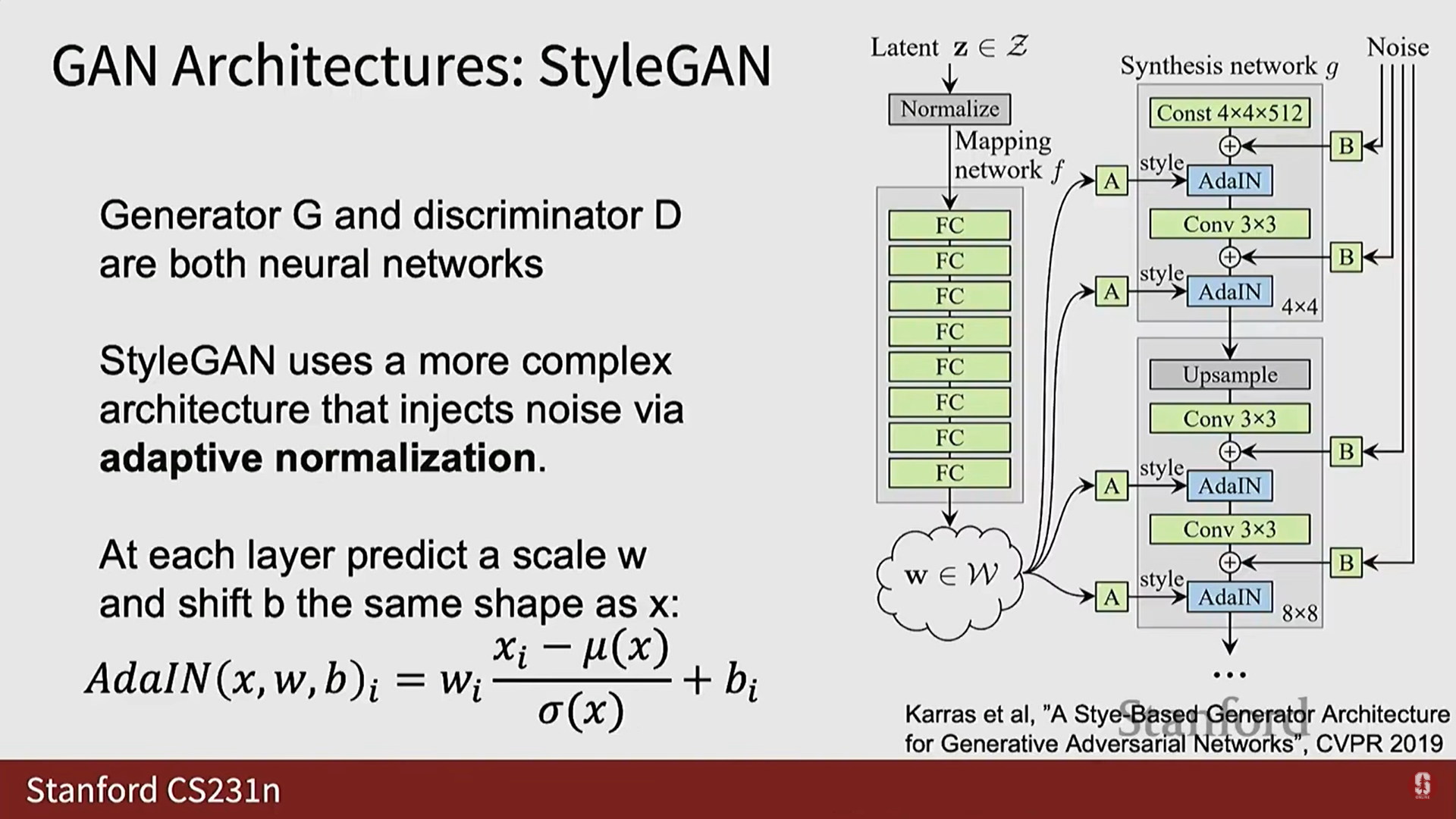
Style GAN: 더 복잡한 아키텍처를 사용하여 매우 좋은 결과를 얻었으며, GAN의 모범 사례를 알고 싶다면 읽어볼 만한 논문이다.
-
잠재 공간의 부드러움 (Smooth Latent Space): GAN의 좋은 특징 중 하나는 잠재 공간을 부드럽게 학습하는 경향이 있다는 것이다.
- 두 잠재 벡터 와 사이를 보간(interpolate)하여 에 통과시키면, 생성된 샘플들이 부드럽게 서로 변형되는 것을 관찰할 수 있다.
- 이는 모델이 잠재 공간에 유용한 구조를 발견했음을 의미한다.

-
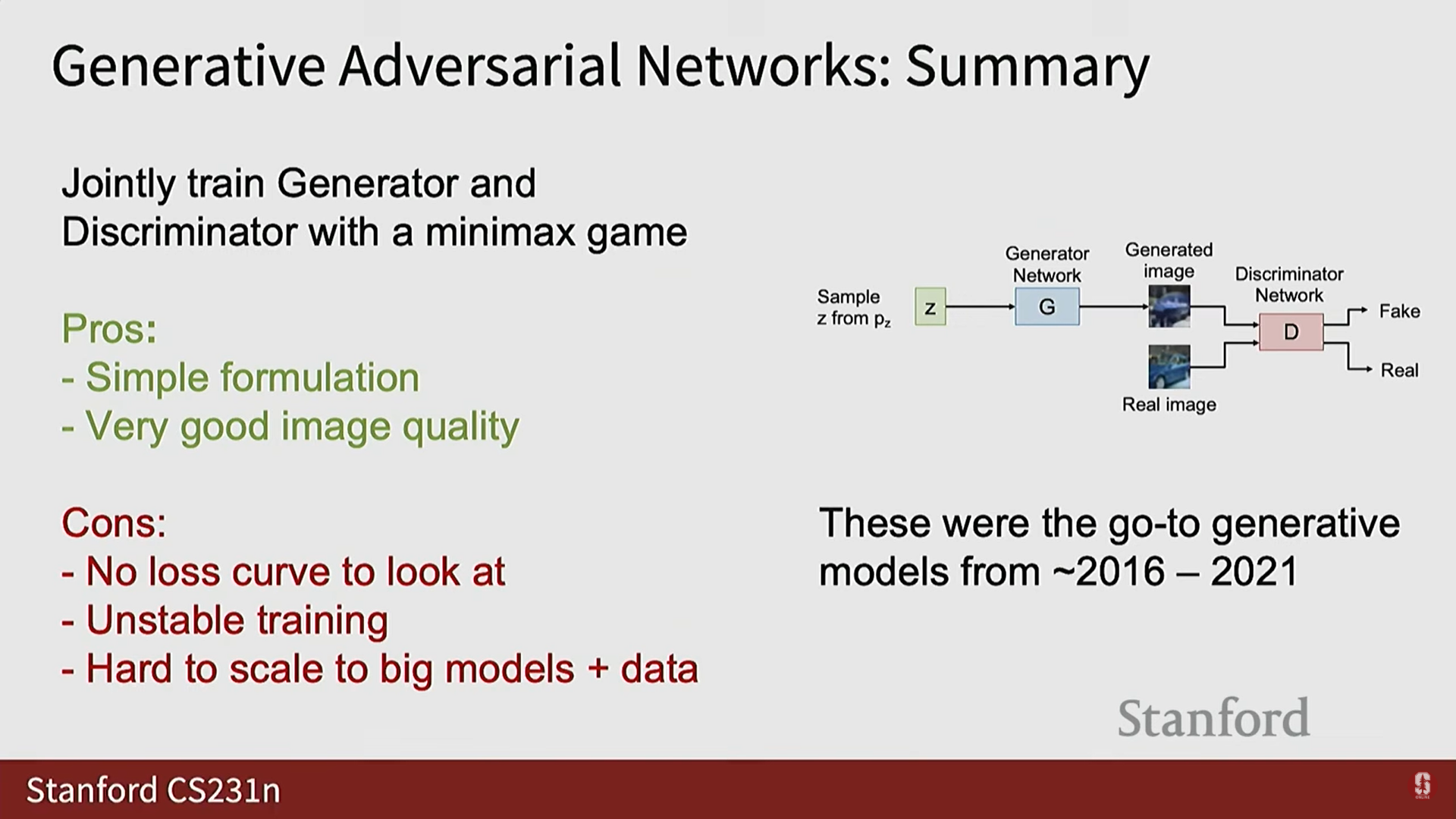
GAN의 장점과 단점:
- 장점: 정식화가 비교적 간단하고, 잘 튜닝하면 Style GAN처럼 매우 깔끔하고 고해상도의 아름다운 이미지를 생성할 수 있다.
- 단점:
- 훈련이 매우 불안정하다.
- 볼 수 있는 손실 곡선이 없다.
- 모드 붕괴 (Mode Collapse)와 같은 문제로 인해 훈련이 쉽게 폭발할 수 있다.
- 대규모 데이터와 대규모 모델로 확장하기 어려웠다.
-
X와 Z의 관계 (Mapping): GAN은 잠재 공간에서 데이터 공간으로의 매핑 ()을 제공하지만, 일반적으로 에서 로 되돌아가는 매핑을 학습할 방법이 없다.
- VAE는 명시적인 매핑을 학습하지만, GAN에서는 판별자가 명시적인 지도 없이 분포 일치를 강제하려고 시도한다.
-
GAN의 가치: VAE는 일반적으로 이미지가 흐릿(blurry)하고 선명하지 않은 반면, GAN은 매우 선명하고 깨끗한 샘플을 제공할 수 있다. 이것이 GAN이 얻은 가장 큰 이점이다.
-
추론 시간: 추론 시에는 판별자를 버리고 생성자만 사용하여, 에서 를 샘플링한 후 를 통과시켜 데이터를 얻으므로 매우 효율적이다.
3. 확산 모델 (Diffusion Models): 새로운 패러다임
확산 모델의 직관적 개요
- GAN이 5~6년 동안 생성 모델링의 대세였지만, 이후 확산 모델 (Diffusion Models)이라는 완전히 다른 범주의 모델이 등장하여 대세가 되었다.
- 확산 모델 문헌은 복잡하며, 다양한 수학적 정식화(SDE, Score Matching 등)와 용어가 혼재되어 있다.
- GAN과의 차이: GAN은 잠재 변수 에서 데이터 로의 결정론적 매핑을 학습하지만, 확산 모델은 더 간접적인 방식을 사용한다.
- 기본 제약 조건: 확산 모델에서 노이즈 분포 는 항상 데이터의 모양(shape)과 정확히 같아야 한다 (예: 이미지 H x W x 3).
노이즈 수준과 점진적 디노이징
- 노이즈 수준 : 0부터 1까지의 범위를 가지며, 데이터에 추가되는 노이즈의 수준을 나타낸다.
- : 노이즈 없음 (완전히 깨끗한 데이터 샘플).
- : 완전한 노이즈 (노이즈 분포에서 직접 샘플링).
- 확산 모델은 데이터 분포와 노이즈 분포 사이를 매개변수를 통해 부드럽게 보간한다. 노이즈 분포는 보통 가우시안이다.
- 훈련 목표: 신경망은 중간 수준의 노이즈가 손상된 데이터 샘플을 입력받아, 노이즈를 조금씩 점진적으로 제거하도록 훈련된다 (incremental denoising).
- 추론 과정: 반복적인 절차를 사용한다.
- 먼저 에서 완전한 노이즈 샘플을 추출한다.
- 이 샘플을 신경망에 반복적으로 적용하여 노이즈를 단계적으로 제거한다.
- 네트워크는 처음에는 완전한 노이즈에서 데이터 구조의 아주 작은 부분을 '환각'(hallucinate)하도록 강제된다.
- 이 과정이 반복되면서 샘플은 점점 덜 노이즈가 섞인 형태로 바뀌고, 결국 모든 노이즈가 제거되어 생성된 샘플을 얻는다.

4. Rectified Flow 모델 (구체적인 확산 모델 구현)
- Rectified Flow는 확산 모델의 한 특정 범주이며, 확산 모델의 개념을 구체화하는 데 유용하다.
- Rectified Flow의 핵심은 (우리가 이해하기 쉬운 단순 분포)와 (우주가 사용하는 복잡한 분포) 사이에 기하학적인 직관을 적용하는 것이다.
1) Rectified Flow의 기하학적 직관
- 훈련 데이터 준비:
- 알려진 사전 분포에서 노이즈 샘플 를 샘플링한다 ().
- 학습 데이터셋에서 데이터 샘플 를 샘플링한다 ().
- 노이즈 수준 를 에서 사이에서 균일하게 선택한다.
- 속도 벡터 : 데이터 샘플 에서 노이즈 샘플 로 직접 향하는 선(line)을 긋고, 이 선을 따라가는 벡터를 (흐름장(flow field)의 속도)라고 정의한다.
- 노이즈 섞인 데이터 : 와 사이를 선형 보간한 지점 를 설정한다.
- 수식: .
- 는 Rectified Flow 모델에서 '노이즈가 섞인 데이터'를 의미하며, 이는 데이터 샘플과 노이즈 샘플 사이의 선형 보간이다.
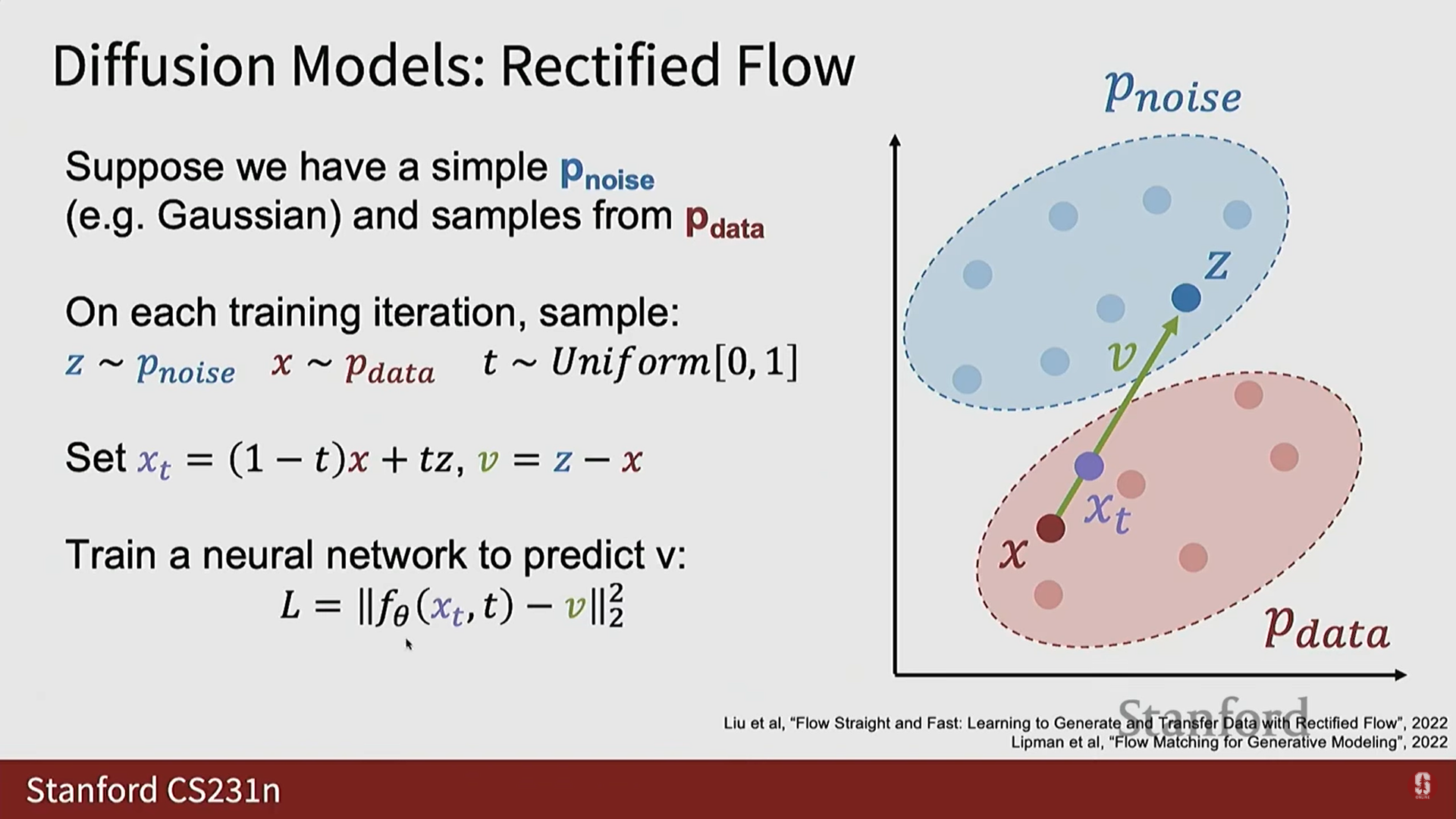
2) Rectified Flow 훈련 목표와 수식
- 신경망 훈련:
- 신경망 는 노이즈가 섞인 샘플 와 노이즈 수준 를 입력받는다.
- 는 녹색 벡터 를 예측하도록 훈련된다.
- 는 에서 로 향하는 지상 진실(Ground Truth) 속도 벡터 이다.
- 수식: .
- 손실 함수 (Loss Function):
- Rectified Flow의 훈련 루프는 매우 간단하다.
- 손실은 지상 진실 속도 와 모델 예측 사이의 평균 제곱 오차(Mean Squared Error, MSE)이다.
- 훈련의 장점: GAN과 달리, Rectified Flow 모델을 훈련할 때 손실 곡선을 볼 수 있다. 손실이 감소하면 모델이 일반적으로 더 좋아진다는 것을 의미한다.

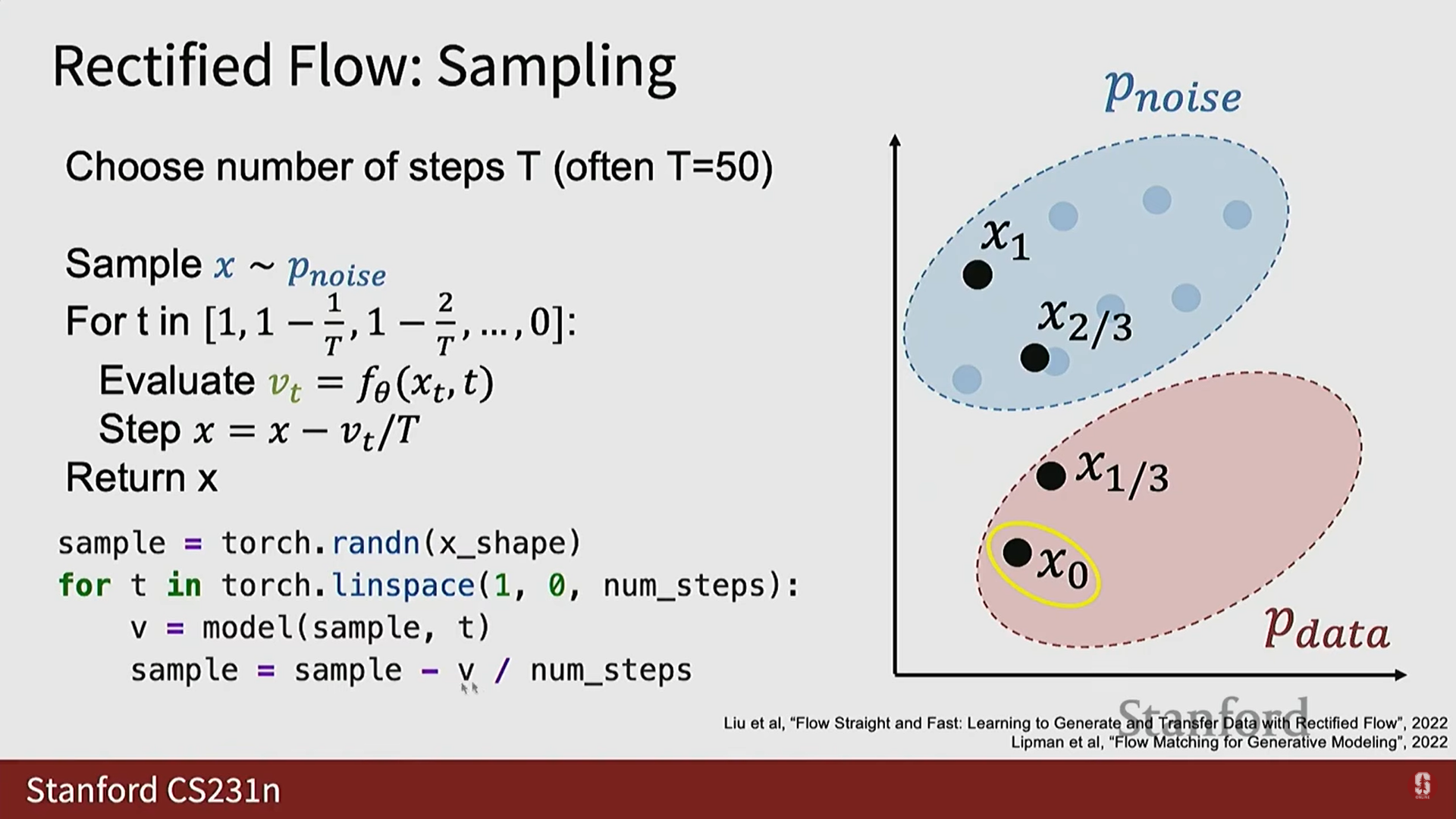
3) Rectified Flow 추론 (Sampling) 과정
- 추론 시에는 모델의 출력 가 데이터 샘플을 직접적으로 주지 않으므로 과정이 GAN보다 복잡해진다.
- 절차:
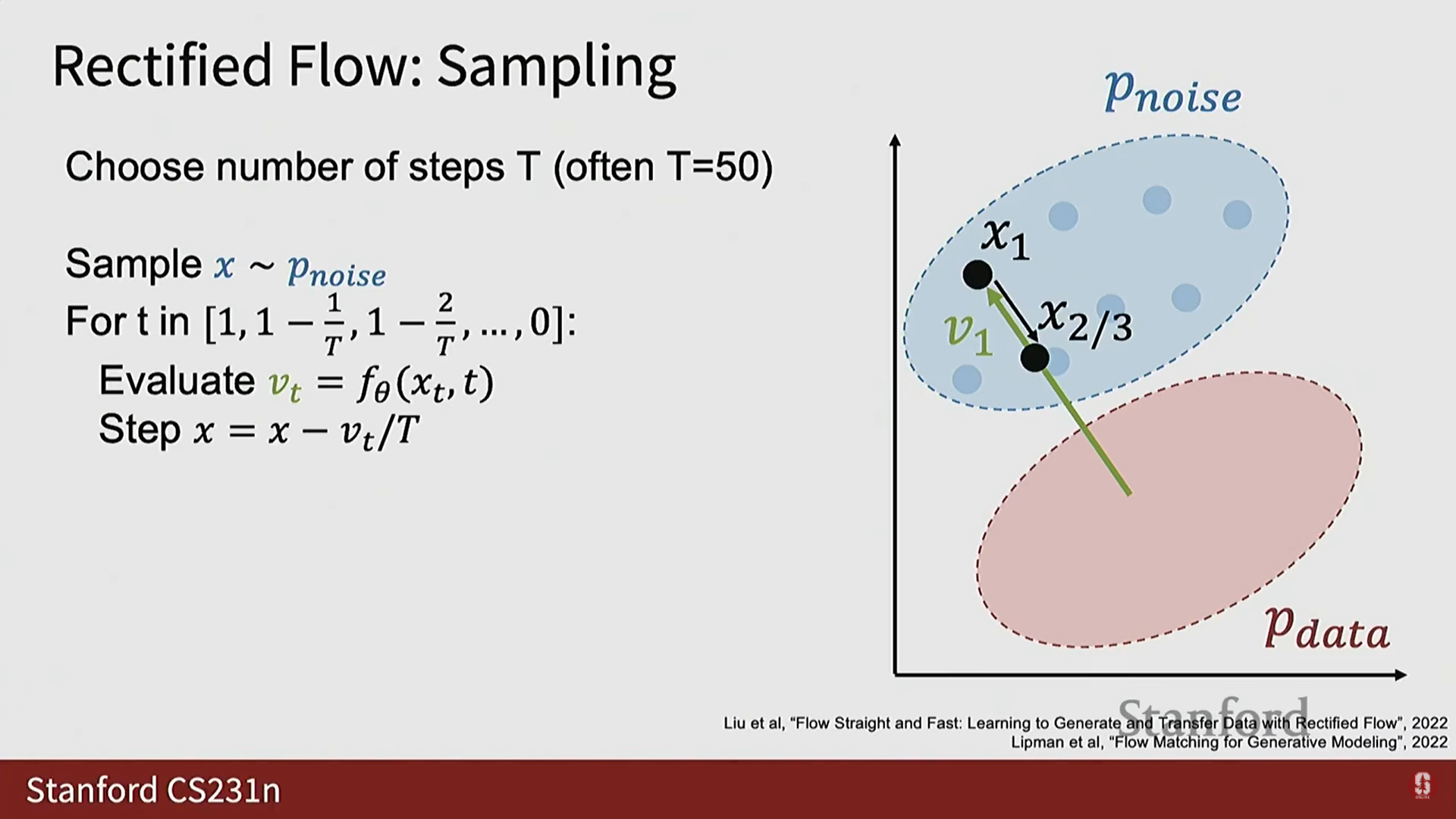
- 추론 단계 수 를 미리 정한다 (일반적으로 정도가 적절하다).
- 노이즈 분포에서 순수한 노이즈 를 샘플링한다 (가장 높은 노이즈 수준 에 해당).
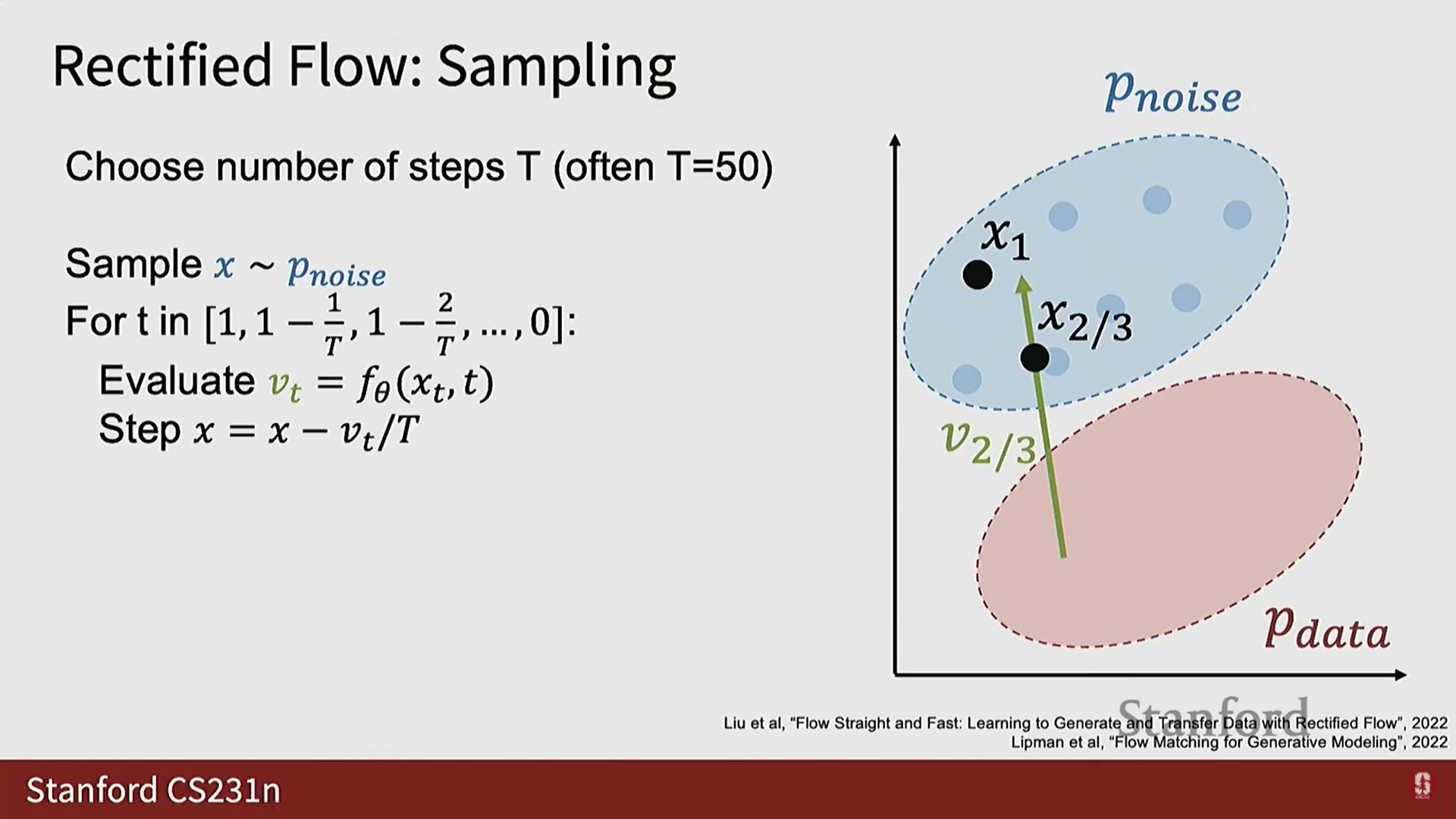
- 에서 까지 (노이즈 수준 1에서 0까지) 반복적으로 마르쉐(march)하며 진행한다.
- 각 반복에서 현재 와 노이즈 수준 를 모델에 전달하여 예측된 를 얻는다.
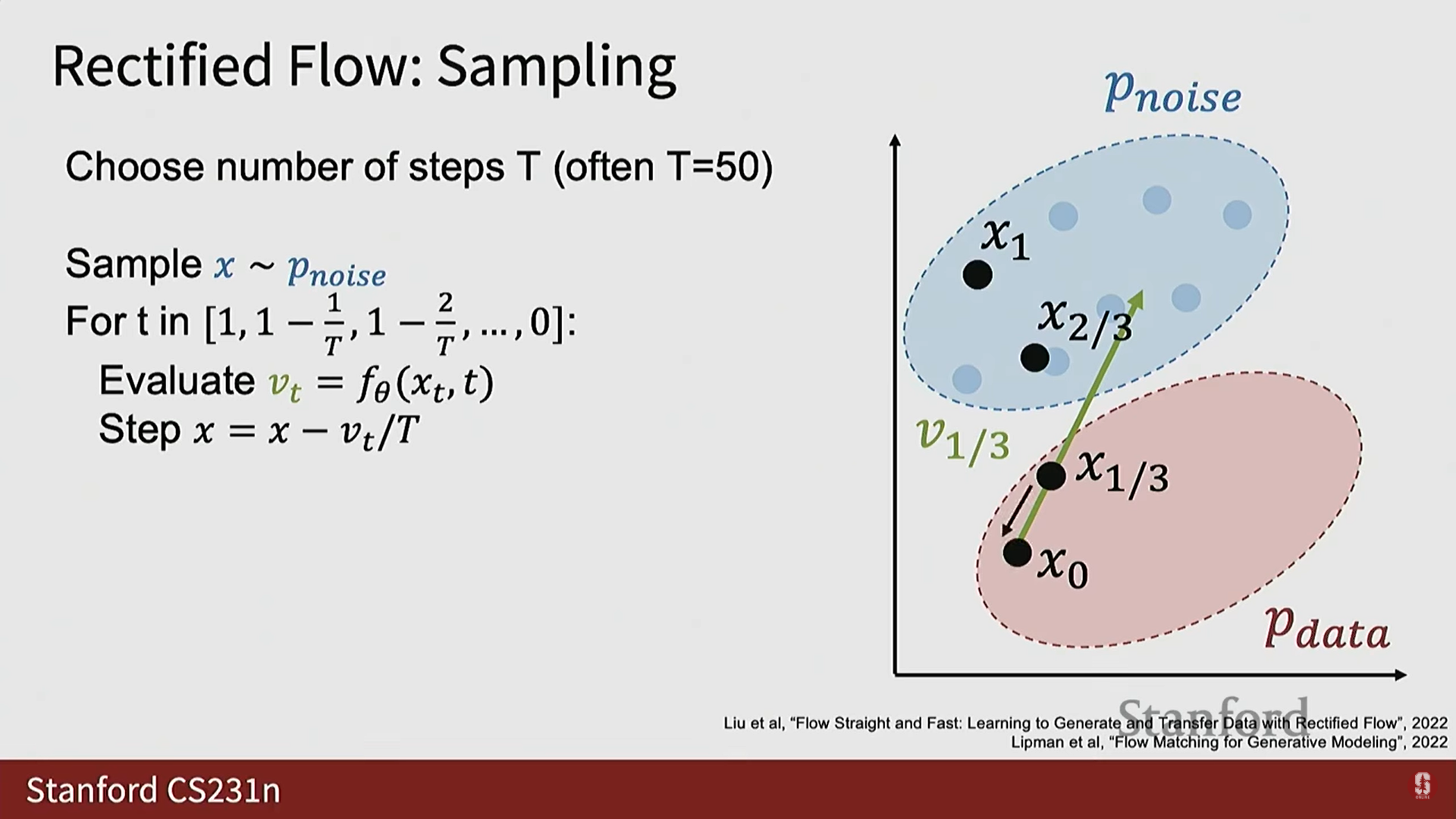
- 이동 (Step): 예측된 벡터를 따라 작은 단계(step)를 밟아 새로운 (노이즈가 약간 제거된 버전)를 얻는다.
- 는 깨끗한 샘플에서 노이즈 샘플로 향해야 하므로, 이 벡터를 따라 단계적으로 이동하면 깨끗한 샘플 궤적을 따라가는 것과 유사하다.
- 이 과정을 반복하여 결국 노이즈가 제거된 예측 를 얻는다.
- 효율성: 추론 절차는 GAN에 비해 더 복잡하지만, 훈련할 때 안정성과 품질을 되찾았다. 확산 모델은 더 나은 샘플을 제공하고 대규모 데이터셋과 모델에 잘 확장되는 경향이 있다.

5. 심화: 조건부 생성 모델링 및 최신 트렌드
1) 잠재 변수와 데이터 샘플의 연결 문제
- 생성 모델링의 핵심 문제는 사전 분포 의 샘플과 데이터 분포 의 샘플을 어떻게 짝지을(pair up) 것인가를 알아내는 것이다.
- VAE는 모델이 를 예측하고 를 예측하도록 하여 를 샘플링 가능한 것으로 강제하며, GAN은 판별자를 통해 분포 일치를 강제하여 매핑을 찾아낸다.
- 확산 모델은 곡선을 통합하는 방식으로 이를 해결한다. 모든 생성 모델링 형태는 훈련 시 와 의 연관성이 없더라도 에서 로의 연관성을 학습하는 방법을 찾는 방식이다.
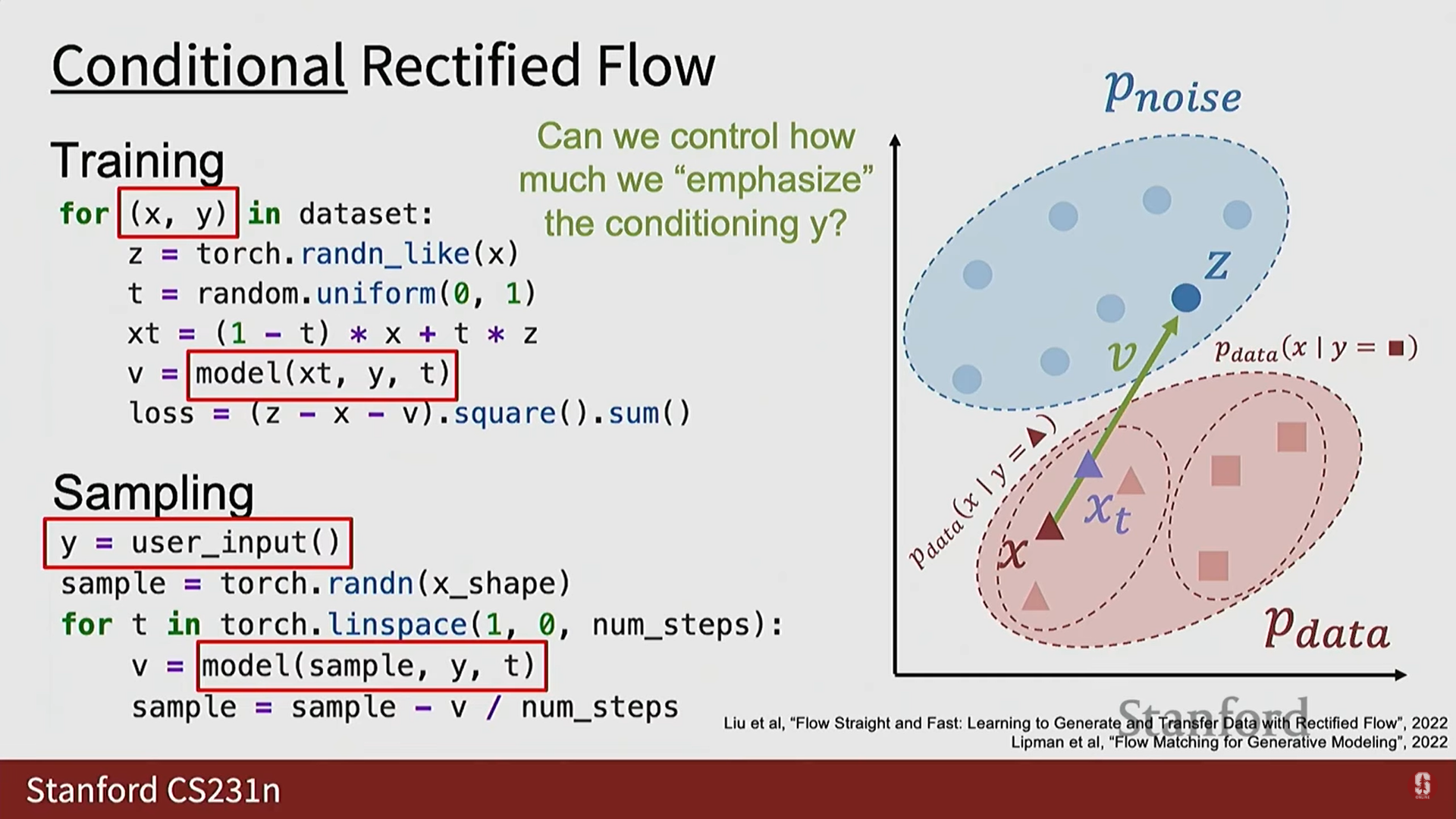
2) 조건부 Rectified Flow 및 Classifier Free Guidance (CFG)
- 비조건부 생성 모델링은 실용적이지 않으므로, 우리는 조건부 생성 모델링에 관심이 있다 ().
- 조건부 Rectified Flow:
- 데이터셋이 쌍을 가지며, 모델이 를 추가적인 보조 입력으로 받는다.
- 추론 시 는 사용자 입력(텍스트 프롬프트, 입력 이미지 등)이 될 수 있으며, 모델을 제어 가능하고 유용하게 만든다.
Classifier Free Guidance (CFG, 분류기 자유 안내) (심화)
- 훈련 시 모델이 조건 신호에 충분히 주의를 기울이지 않는 경우가 많다. CFG는 이를 조정하는 기법이다.
- 훈련 트릭: 조건부 확산 모델을 훈련할 때, 매 훈련 반복마다 동전을 던져 50%의 확률로 조건 정보 를 삭제(null 값으로 설정)한다.
- 결과: 모델은 개념적으로 두 가지 다른 속도 벡터를 학습하도록 강제된다.
- 무조건부 속도 벡터 (): 가 삭제되었을 때, 전체 데이터 분포 의 중심으로 향한다.
- 조건부 속도 벡터 (): 실제 조건부 입력 가 주어졌을 때, 조건부 데이터 분포 의 중심으로 향한다.
- 안내 (Guidance) 적용: 스칼라 하이퍼파라미터 를 사용하여 두 벡터를 선형 결합한다.
- 값이 높을수록 조건부 신호에 더 강조를 두어 조건부 분포 쪽으로 더 많이 밀어내는 효과를 얻는다.
- 추론 시: 매 반복마다 모델을 두 번 평가하여 와 을 모두 얻은 다음, 이 선형 결합 를 따라 단계를 밟아 샘플링한다.
- 이름 유래: 초기에 분류기(classifier)를 사용한 안내(guidance) 방법이 있었으나, 이 방법은 분류기를 제거했기 때문에 '분류기 자유 안내'라는 이름이 붙었다.
- 비용: CFG는 추론 시 모델을 매번 두 번 호출해야 하므로 샘플링 비용을 두 배로 만든다.



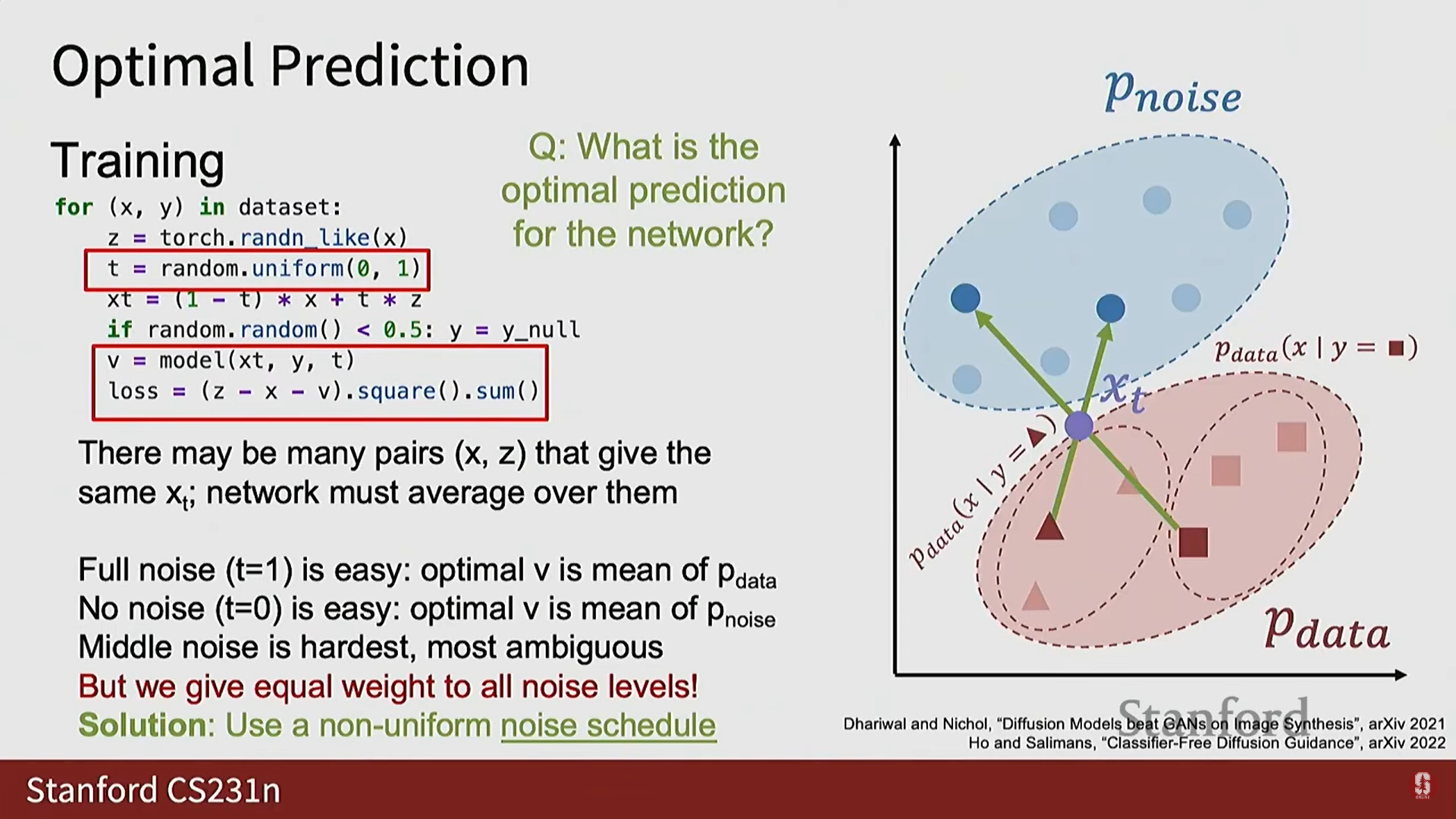
3) 노이즈 스케줄 (Noise Schedules)의 중요성
- 훈련 시 를 균일 분포에서 샘플링하면 모든 노이즈 수준에 동일한 중요도를 부여하게 된다.
- 문제: 완전한 노이즈()나 노이즈 없음() 상태에서는 모델의 최적 예측이 데이터 분포의 평균을 향하는 등 문제가 비교적 쉽다. 그러나 중간 단계에서는 동일한 를 생성했을 수 있는 여러 와 쌍이 존재할 수 있어 문제가 훨씬 어렵다.
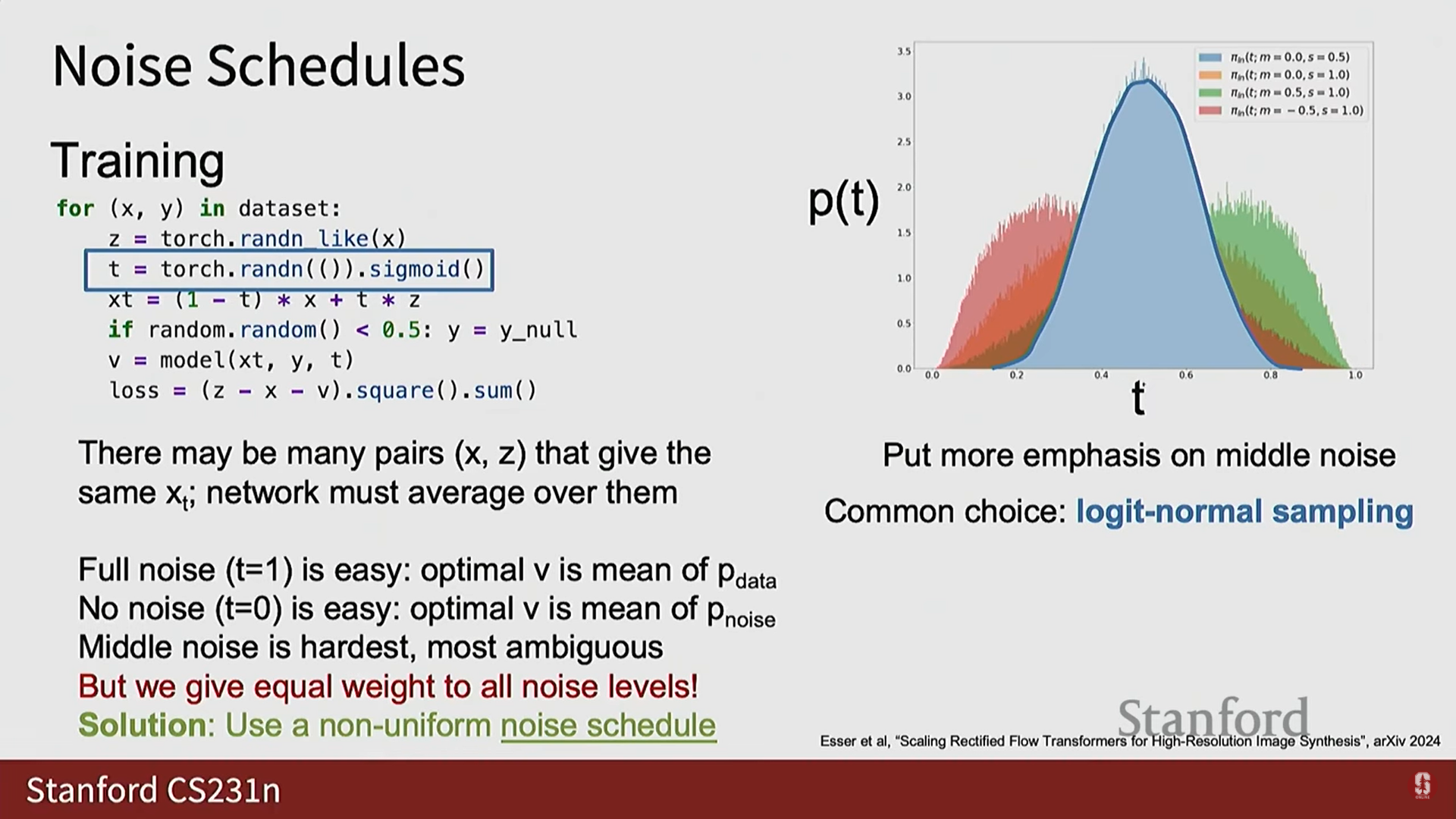
- 해결책: 이러한 직관과 일치시키기 위해 실제로는 균일 분포가 아닌 다른 노이즈 스케줄(noise schedules)에서 를 샘플링하는 경우가 많다.
- Logit Normal Sampling: 0과 1에 상대적으로 적은 가중치를 두고 중간에 더 많은 가중치를 두는 가우시안 형태의 스케줄이다.
- 고해상도 데이터로 확장할 때, 데이터의 픽셀 간 상관관계 정도에 따라 적절한 노이즈 수준이 필요하기 때문에 비대칭적인 Shifted Noise Schedules도 사용된다.



4) 잠재 확산 모델 (Latent Diffusion Models, LDM) (심화)
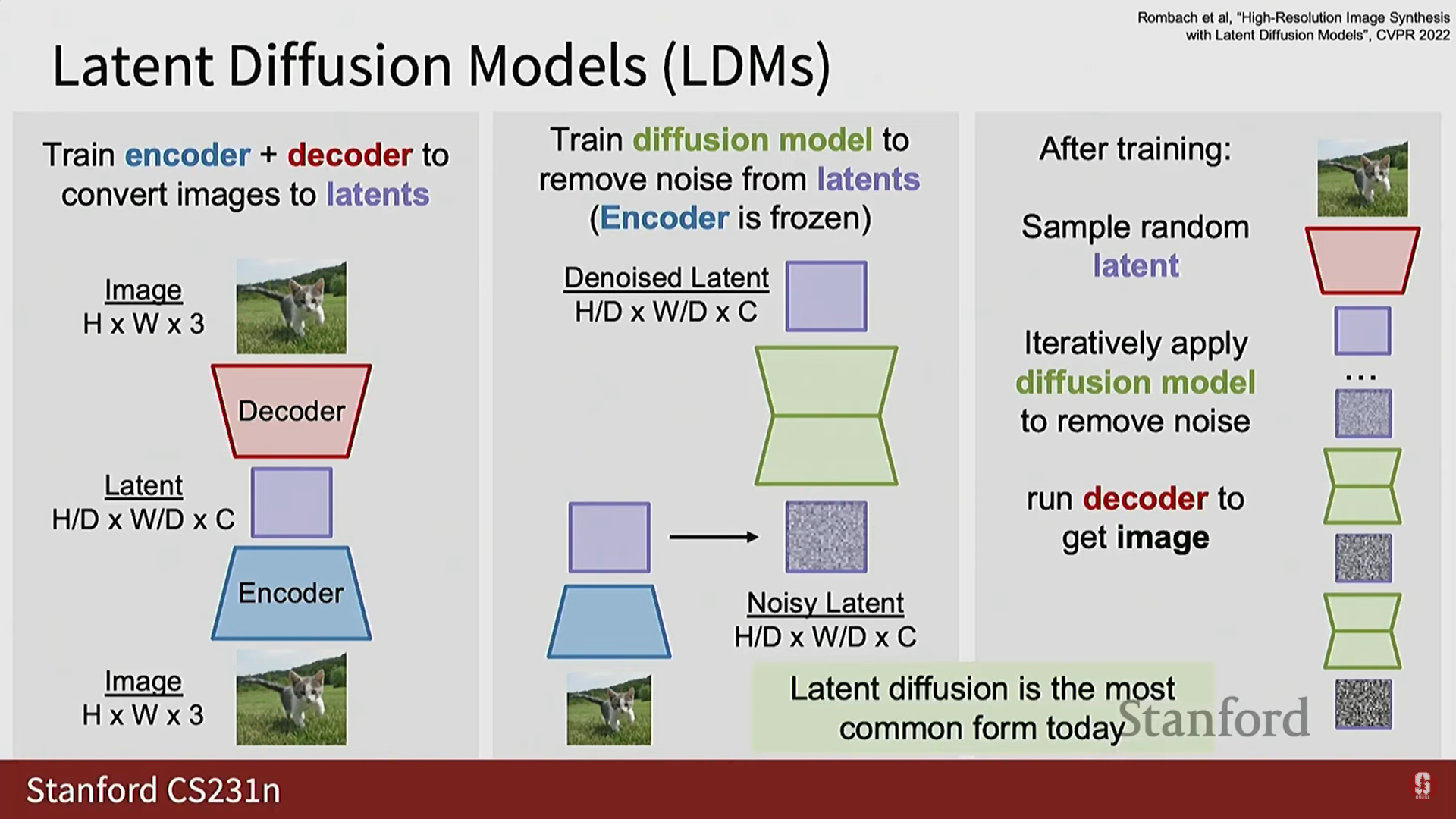
- 확산 모델을 고해상도 데이터에 순수하게 적용하기 어렵다는 문제 때문에 등장했다.
- LDM 파이프라인: 다단계 절차를 사용한다.
- 인코더/디코더 훈련:
- 먼저 인코더 네트워크를 훈련하여 이미지를 잠재 공간(latent space)으로 매핑한다.
- 잠재 공간은 일반적으로 이미지의 공간 해상도를 만큼 다운샘플링하고 채널 수를 만큼 증가시킨다 (예: 8x8 다운샘플링, 16채널).
- 이 인코더/디코더 구조는 종종 변이형 자기부호화기 (VAE)를 사용하여 훈련된다.
- 확산 모델 훈련:
- 원본 픽셀 공간이 아닌, 인코더가 발견한 잠재 공간에서 확산 모델을 훈련한다.
- 이미지를 인코더에 통과시켜 잠재 코드를 얻고, 이 잠재 코드에 노이즈를 추가한 후, 확산 모델이 노이즈가 추가된 잠재 코드를 디노이징하도록 훈련한다.
- 중요: 인코더를 고정(freeze)하고, 그래디언트를 인코더로 역전파하지 않는다.
- 추론:
- 무작위 잠재 코드를 샘플링하고, 확산 모델을 여러 번 반복하여 노이즈를 제거한 깨끗한 잠재 코드를 얻는다.
- 이 깨끗한 잠재 코드를 디코더를 통해 깨끗한 이미지로 변환한다.
- 인코더/디코더 훈련:
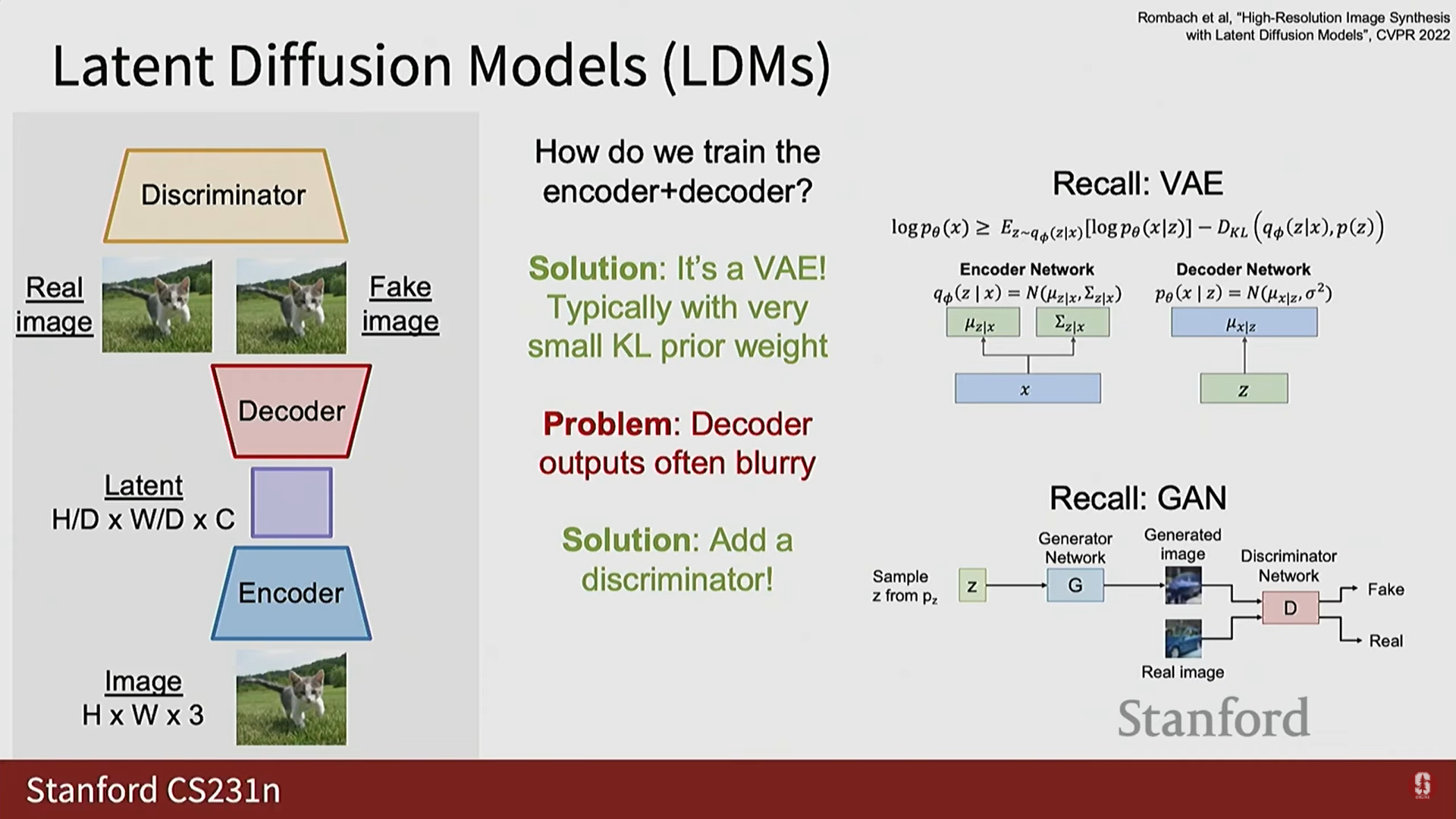
- LDM의 구성 (VAE와 GAN의 통합):
- VAE는 출력이 흐릿하다는 큰 문제가 있다. 만약 인코더/디코더가 흐릿한 재구성을 제공한다면, 이는 다운스트림 확산 모델의 생성 품질에 병목 현상을 일으킨다.
- 따라서 실제로 LDM의 인코더-디코더는 VAE와 GAN의 조합으로 훈련되는 경향이 있다. 즉, 디코더 다음에 판별자를 두어 재구성 품질을 높인다.
- 현대 생성 모델링 파이프라인은 VAE, GAN, 확산 모델을 모두 훈련하는 복잡한 구조를 포함한다.
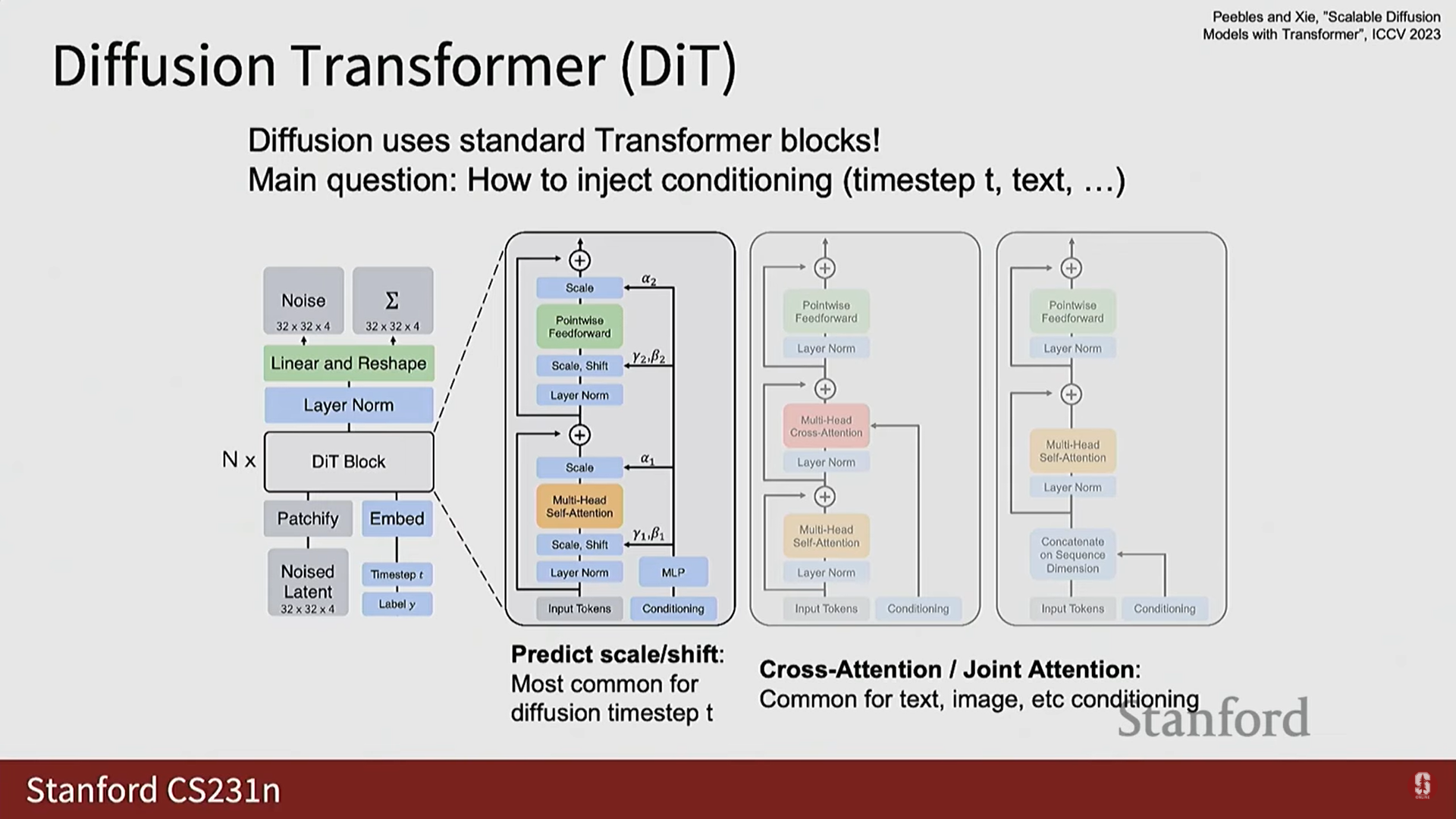
5) 확산 트랜스포머 (Diffusion Transformers, DiTs)
- 최근 몇 년간 비교적 간단한 트랜스포머(Transformers) 구조가 확산 모델에 적용되어 매우 잘 작동함이 밝혀졌다 (Diffusion Transformers, DiTs).
- 조건 정보 주입: DiTs의 핵심 건축 문제는 노이즈가 섞인 이미지, 타임스탬프 , 조건부 신호(예: 텍스트)의 세 가지 입력을 어떻게 주입할 것인가이다.
- 타임스탬프 주입: 일반적으로 스케일 및 시프트(scale and shift)를 예측하여 확산 블록의 중간 활성화(intermediate activations)를 변조하는 방식으로 주입된다.
- 텍스트/기타 조건 주입: 모든 것을 시퀀스에 넣고 트랜스포머가 전체 데이터 시퀀스를 모델링하게 할 수 있다. 이는 일반적으로 교차 어텐션(cross attention) 또는 결합 어텐션(joint attention)을 통해 수행된다.
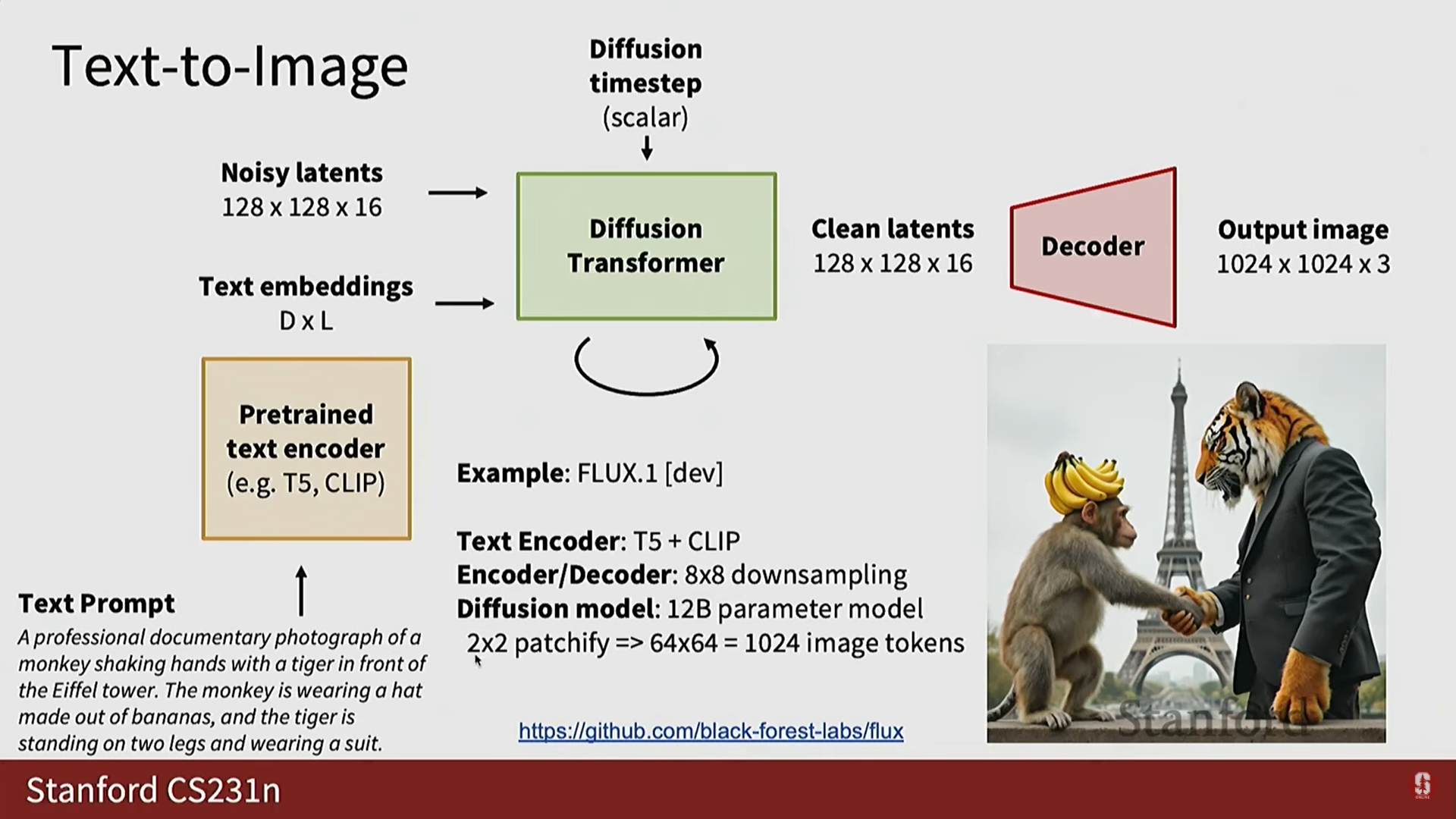
6) 텍스트-이미지 및 텍스트-비디오 생성
(1) 텍스트-이미지 생성
- 파이프라인: 텍스트 프롬프트를 사전 훈련된 텍스트 인코더 (T5, CLIP 등, 보통 고정됨)에 통과시켜 텍스트 임베딩을 얻는다.
- 이 텍스트 임베딩을 노이즈가 섞인 잠재 코드 및 확산 타임스텝과 함께 확산 트랜스포머에 입력한다.
- 디노이징 과정을 거쳐 깨끗한 잠재 코드를 얻고, VAE 디코더를 통해 최종 이미지를 생성한다.
- 예시 (Flux One Dev): T5 및 CLIP 인코더를 사용하며, VAE가 8배 다운샘플링을 하고, 그 위에 120억 개의 매개변수를 가진 트랜스포머를 훈련하여 1024개의 이미지 토큰 시퀀스를 처리한다.
(2) 텍스트-비디오 생성 (최신 동향)
- 파이프라인: 텍스트-이미지 파이프라인과 유사하다. 유일한 주요 차이점은 잠재 코드에 시간(time)을 위한 추가 차원이 생긴다는 것이다.
- 디코더는 이제 공간-시간적 자기부호화기(spatial-temporal auto-encoder)가 되어 공간적 및 시간적 다운샘플링을 모두 수행한다.
- 문제점 (명확한 한계점): 비디오 생성 모델은 높은 프레임 속도와 고해상도를 생성하려면 매우 긴 시퀀스 길이가 필요하므로 훈련 비용이 매우 비싸다.
- 텍스트-이미지 모델이 1024개의 이미지 토큰을 처리하는 반면, 최신 텍스트-비디오 모델은 고해상도 비디오를 위해 76,000개의 비디오 토큰을 처리해야 할 수 있다.
- 최신 동향: 지난 1년 반 동안 비디오 확산 모델은 매우 뜨거운 주제였다.
- OpenAI Sora (2024년 3월): 비디오 확산 모델에서 '4분 마일'과 같은 순간을 제공한, 정말 좋은 결과를 보여준 최초의 모델이었다.
- Google Veo 3 (최신 발표): 강의 당일 발표되었으며, 현존하는 최고의 비디오 생성 모델일 가능성이 높다. 비디오 프레임과 함께 오디오도 공동으로 모델링할 수 있다.

(3) 추론 속도 문제 및 증류 (Distillation)
- 느린 추론 속도: 확산 모델은 샘플링 시 반복적인 절차(iterative procedure)가 필요하기 때문에 추론 시간이 매우 느리다. Rectified Flow에서도 좋은 샘플을 얻으려면 수십 번의 반복(30~50회)이 필요하며, 모델이 수십억 개의 매개변수를 가질 수 있기 때문에 문제가 된다.
- 해결책: 증류 (Distillation):
- 증류 알고리즘은 추론 시 적은 횟수의 반복만으로도 좋은 샘플을 얻을 수 있도록 모델을 수정하는 방법이다.
- 이 기술의 핵심은 샘플 품질을 최대한 유지하면서 추론 단계 수를 줄이는 것이다.
- 일부 증류 방법은 단일 단계 샘플링(single-step sampling)까지 가능하게 하지만, 이 경우 생성 품질은 다소 희생될 수 있다. 이는 현재 매우 활발한 연구 영역이다.

7) 확산 모델의 다양한 수학적 공식화 (심화)
- Rectified Flow는 기하학적 직관을 제공했지만, 확산 모델에는 다양한 수학적 정식화가 존재한다.
- 일반화된 확산 모델에서는 다음 네 가지 기능적 하이퍼파라미터가 변경될 수 있다:
- 분포 (노이즈 수준 를 샘플링하는 분포).
- 노이즈 섞인 를 계산하는 방법 (일반적으로 와 의 선형 결합의 함수).
- 모델이 예측하도록 요청받는 지상 진실 목표 (일반적으로 와 의 선형 결합).

- Rectified Flow: 와 가 모두 간단한 선형 형태를 취한다.
- Variance Preserving (분산 보존) / Variance Exploding (분산 폭발): 이들은 를 계산하는 선형 결합 가중치를 와 같은 하나의 스칼라 하이퍼파라미터로 통합하는 다른 정식화이다.


- 모델 예측 목표: 모델은 때로는 깨끗한 데이터 자체를 예측하거나, 추가된 노이즈를 예측하거나, 두 가지의 선형 결합을 예측하도록 요청받을 수 있다.

확산 모델을 바라보는 세 가지 수학적 관점
- 이러한 기능적 하이퍼파라미터를 설정하려면 수학적 지침이 필요하며, 확산 모델을 훈련할 때 사람들이 생각하는 세 가지 주요 수학적 관점이 있다:
- 잠재 변수 모델 (Latent Variable Model):
- 깨끗한 데이터 와 연관된 일련의 손상된 샘플들이 잠재 변수처럼 존재한다고 본다.
- VAE와 매우 유사한 수학적 트릭을 사용하여 데이터의 우도에 대한 변이적 하한을 최대화함으로써 해석된다.
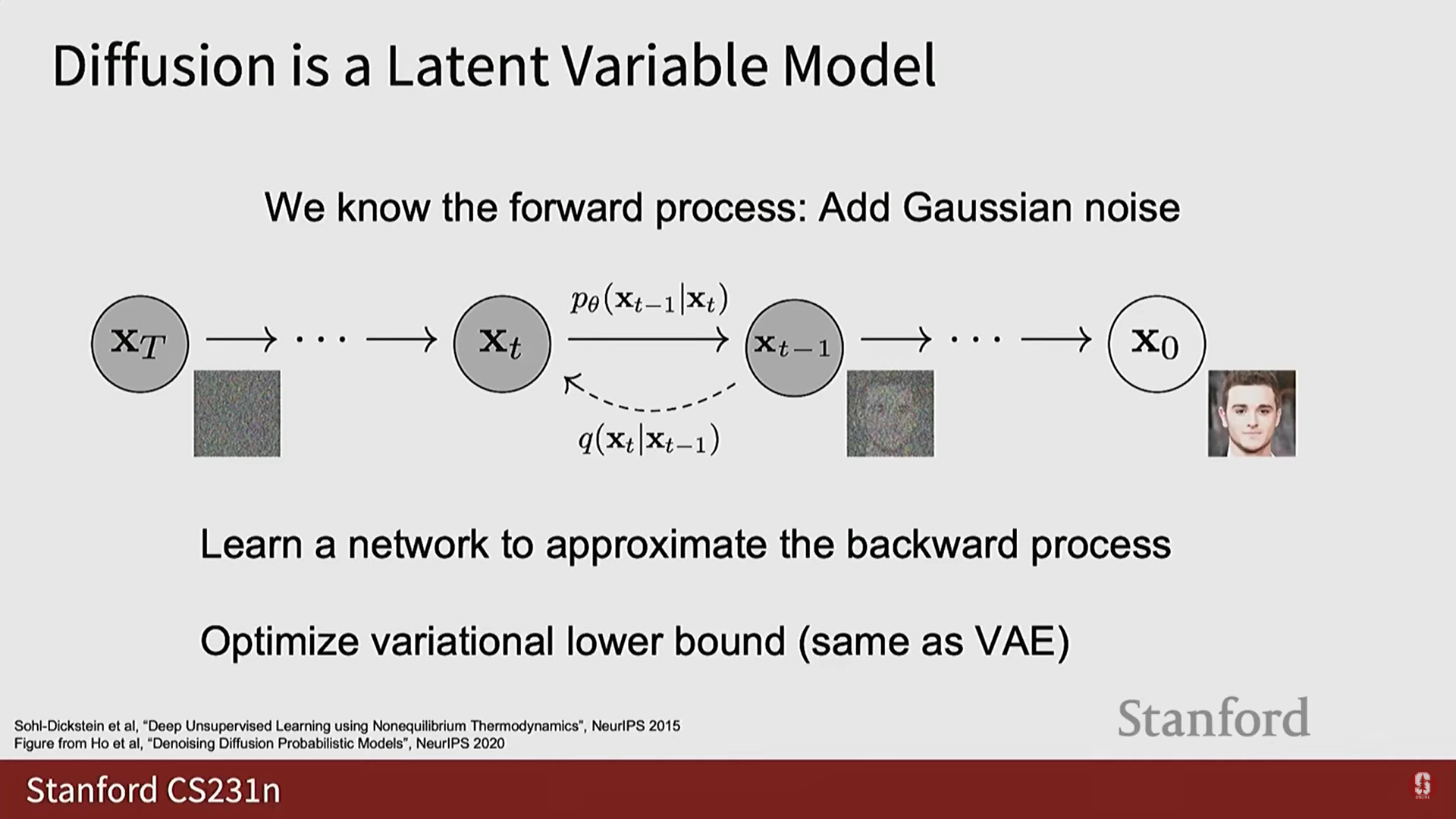
- 점수 함수 (Score Function):
- 분포 의 점수 함수는 로 정의되며, 직관적으로 높은 확률 밀도 영역을 향하는 벡터 필드이다.
- 이 해석에서 확산 모델은 데이터 분포의 점수 함수를 학습하고 있으며, 특히 데이터 분포에 다양한 수준의 노이즈가 섞인 분포에 해당하는 점수 함수 세트를 학습한다.

- 확률 미분 방정식 (Stochastic Differential Equations, SDE):
- 노이즈 분포의 샘플을 데이터 분포의 샘플로 변환하는 무한소(infinitesimal) 방법을 기술하는 미분 방정식을 설정하려고 한다.
- 추론 시 신경망은 우리가 설정한 이 확률 미분 방정식에 대한 수치 적분기(numeric integrator) 역할을 한다.
- Rectified Flow에서 본 단순한 경사 하강 유형 접근 방식은 SDE에 대한 순방향 오일러(forward Euler) 유형 적분기에 해당한다.

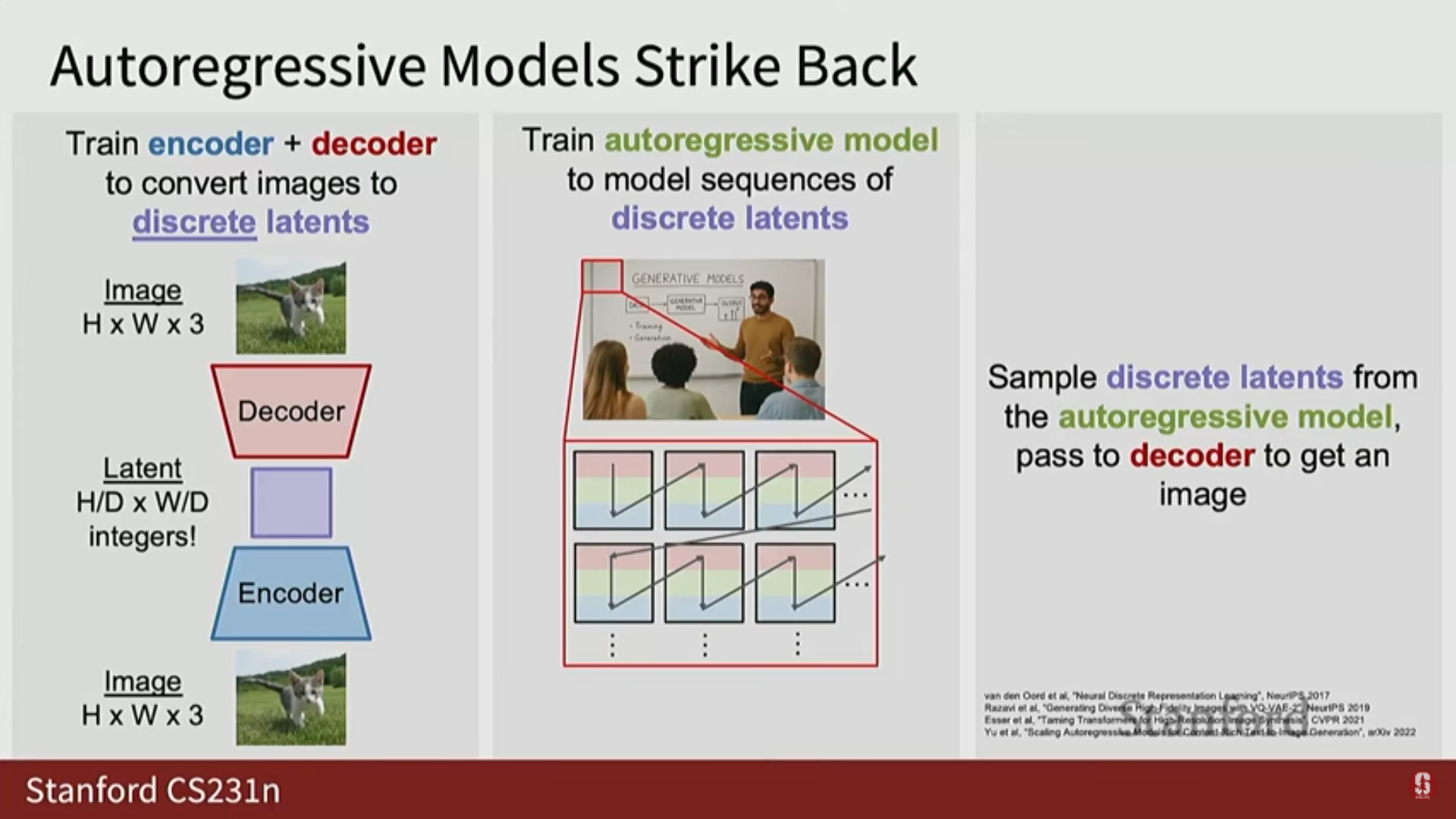
8) 자기회귀 모델의 복귀
- 확산 모델 외에도, 또 다른 현대적인 생성 모델링 레시피는 이산 변이형 자기부호화기 (Discrete VAE)에 의해 계산된 이산 잠재 코드에 대해 자기회귀 모델을 훈련하는 것이다.
- 이는 현대 머신러닝 파이프라인에서 GAN, VAE, 자기회귀 모델, 확산 모델이 모두 사용되고 있음을 보여준다.
6. Q & A (질의응답)
- Q: 생성자 네트워크가 판별자로부터 피드백을 받나요?
- A: 예, 이는 전체 과정의 작동에 매우 중요하며, 받는 피드백 유형은 그래디언트이다. 생성된 이미지를 통해 판별자에서 생성자로 그래디언트가 역전파된다. 생성자의 매개변수에 대한 그래디언트를 얻는 유일한 방법은 판별자를 통하는 것이다.
- Q: 데이터셋을 어떻게 구성하나요? 예를 들어 유니콘 사진이 없는데 어떻게 유니콘 사진을 생성할 수 있나요?
- A: 모델이 샘플을 생성할 수 있는 유일한 방법은 훈련 데이터셋에 그것과 유사한 무언가가 있어야 한다는 것이다. 모든 생성 모델과 신경망은 약간의 일반화 능력을 가지고 있다. 예를 들어, 실제와 같은 유니콘 이미지를 본 적이 없더라도 말 사진, 산타클로스 모자 사진, 유니콘 그림 등을 보았다면 모델은 이러한 속성들의 구성을 일반화하여 새로운 것을 생성할 수 있다.
- Q: 판별자가 유니콘이 실제로 존재하지 않는다는 것을 알 만큼 똑똑한가요?
- A: 판별자가 정말 똑똑하다면 유니콘이 실제로 존재하지 않는다는 것을 알 수도 있지만, 이는 매우 어려운 의미론적 문제이다. 실제로 판별자는 샘플 자체의 질감, 조명, 그림자 등 내부적인 증거만을 보고 판단하는 경향이 있다.
- Q: 판별자 손실 곡선과 생성자 손실 곡선을 따로 보면 안 되나요?
- A: 시도할 수 있지만, 일반적으로는 쓸모가 없다. GAN 목표 함수를 해석 가능하게 만들려는 수백 편의 연구 논문이 있었지만, 5년 동안 수천 명의 사람들이 노력했음에도 불구하고 좋은 해결책은 나오지 않았다고 본다.
- Q: 훈련 초기에 판별자가 너무 빨리 좋아지는 것이 중요한가요?
- A: 그렇지 않다. GAN 훈련은 우리가 이전에 본 어떤 분류 문제와도 다르다. 이는 비정지 분포(non-stationary distribution) 문제이다. 훈련 과정에서 생성자가 더 나아짐에 따라 판별자가 분류하려고 하는 데이터셋 자체가 지속적으로 변화하기 때문이다.
- Q: GAN이 지역 최소점(local minima)에 갇히나요?
- A: 수백 편의 논문과 수많은 경험적 휴리스틱(heuristics)이 있었지만, 갇히지 않게 하는 확실한 방법은 없는 것으로 보인다.
- Q: 분포는 훈련 내내 고정되어 있나요?
- A: 네, 분포는 훈련 과정 내내 고정되어 있다.
- Q: VAE로 돌아갈 때 잠재 벡터를 얻었지만 밀도를 포기했고, GAN에서는 잠재 벡터 제어를 포기했는데, 무엇을 얻었나요?
- A: 훨씬 더 좋은 샘플을 얻었다. VAE는 특성상 흐릿한 경향이 있으며 깨끗하고 선명한 샘플을 제공하지 못하지만, GAN은 매우 선명하고 좋은 품질의 샘플을 얻을 수 있다.
- Q: 확산 모델의 단계 수 는 고정된 하이퍼파라미터인가요?
- A: 확산 모델의 다양한 정식화(formalisms)에 따라 다르다. 이 강의 슬라이드에서는 노이즈 정의, 노이즈 제거 방식, 반복적 적용 방식 등 모든 것이 의도적으로 모호하게 언급되었다. 구체적인 확산 모델 구현에 따라 이러한 용어의 구체적인 선택이 달라진다.
- Q: 훈련 데이터셋과 잠재 코드 의 관계는 무엇인가요?
- A: GAN은 생성자()를 통해 잠재 공간에서 데이터 공간으로의 매핑을 제공하지만, 일반적으로 에서 로 되돌아가는 매핑을 학습할 방법이 없다. 와 사이에 명시적으로 강제된 관계는 없으며, 판별자는 명시적 지도 없이 분포 일치를 강제하려고 시도한다.
