[CV] CS231N 15강 정리 [3D Vision]

김성윤(Jack)·2025년 10월 6일

CV

목록 보기

15/36

1. 개요

강의 소개 및 개요

본 강의는 Stanford 컴퓨터 과학과 조교수인 Jajun Wu 교수가 진행하며, 3D 비전(3D understanding)을 주제로 다룬다.
Wu 교수는 장면 이해(Scene Understanding), 멀티모달 지각(Multimodal Perception), 로보틱스(Robotics), Embodied AI, 시각 생성 및 추론(Visual Generation and Reasoning) 분야를 연구하고 있다.
이번 강의는 컨볼루션 신경망(CNN), 트랜스포머(Transformer), 비전 언어 모델, 생성 모델 등 지난 몇 주간 다룬 2D 기반의 내용들과는 다소 다른, 3D 표현 및 딥러닝 통합 방식을 다룬다.
주요 내용은 3D 표현 방식, 딥러닝이 3D 비전을 어떻게 변화시켰는지, 그리고 3D 생성 및 재구성과 같은 다양한 응용 분야이다.

2. 3D 객체 표현 방식 (3D Representations)

1) 2D와 3D 표현의 차이점

2D 이미지 표현은 픽셀(pixels)로 매우 직관적이고 간단하다 (예: PNG 또는 JPEG 파일의 200x200 행렬).
반면, 3D 객체는 규모가 다양하고(대형 건물부터 미세 구조까지), 기하학(Geometry), 텍스처(Textures), 재질(Materials) 등 다양한 요소를 포함하며, 이를 표현하는 방식이 통일되어 있지 않다.

2) 3D 표현 선택 기준

3D 표현 방식을 선택할 때는 저장 방식, 새로운 형태 생성 지원 여부, 다양한 연산(편집, 단순화, 스무딩, 복구), 렌더링 (3D를 2D 픽셀로 변환), 역 렌더링 (2D 이미지로부터 3D 재구성), 애니메이션 지원, 그리고 딥러닝 방법론과의 통합 등 여러 요소를 고려해야 한다.

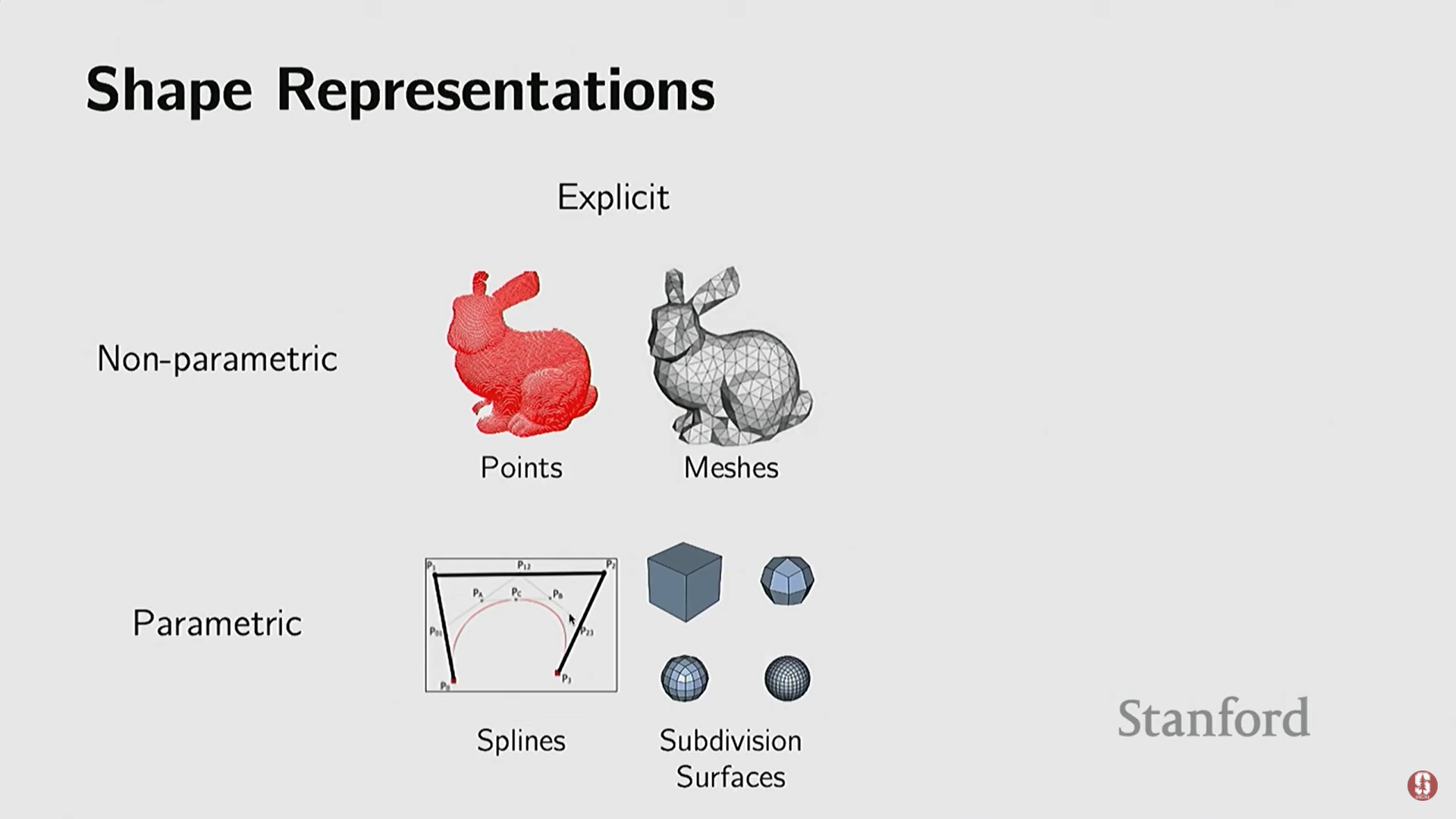
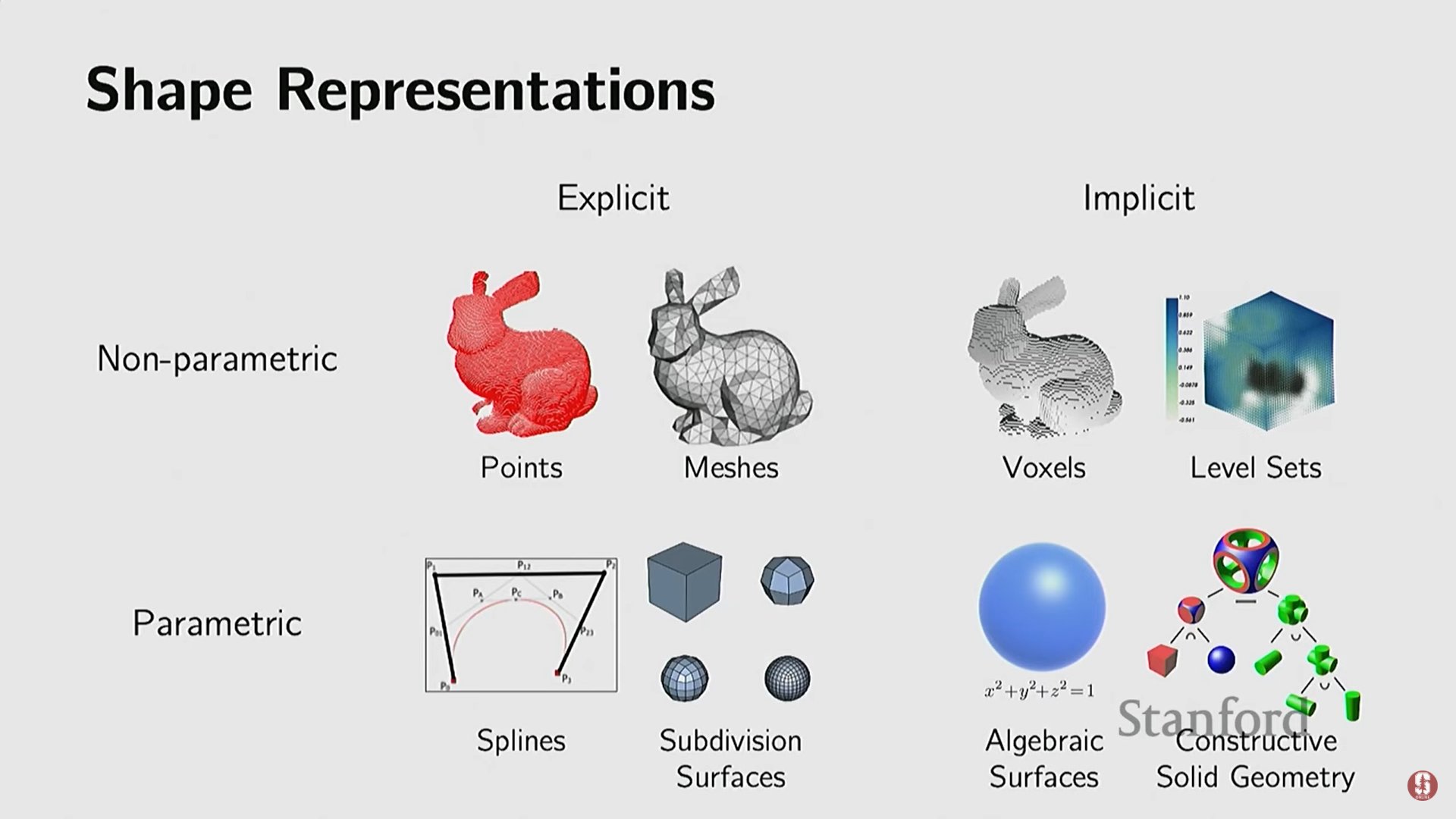
3) 명시적 표현 (Explicit Representations)

객체의 일부를 직접적이고 명시적으로 나타내는 방식이다.
장점: 객체 표면 위의 점들을 직접적으로 얻기 쉽기 때문에, 샘플링이 매우 쉽다.
단점: 특정 점이 객체 내부에 있는지 외부에 있는지 (Inside/Outside 테스트) 판단하기 어렵다. 이는 최근의 뉴럴 렌더링(Neural Rendering) 방식에서 문제가 될 수 있다.

(1) 포인트 클라우드 (Point Clouds)

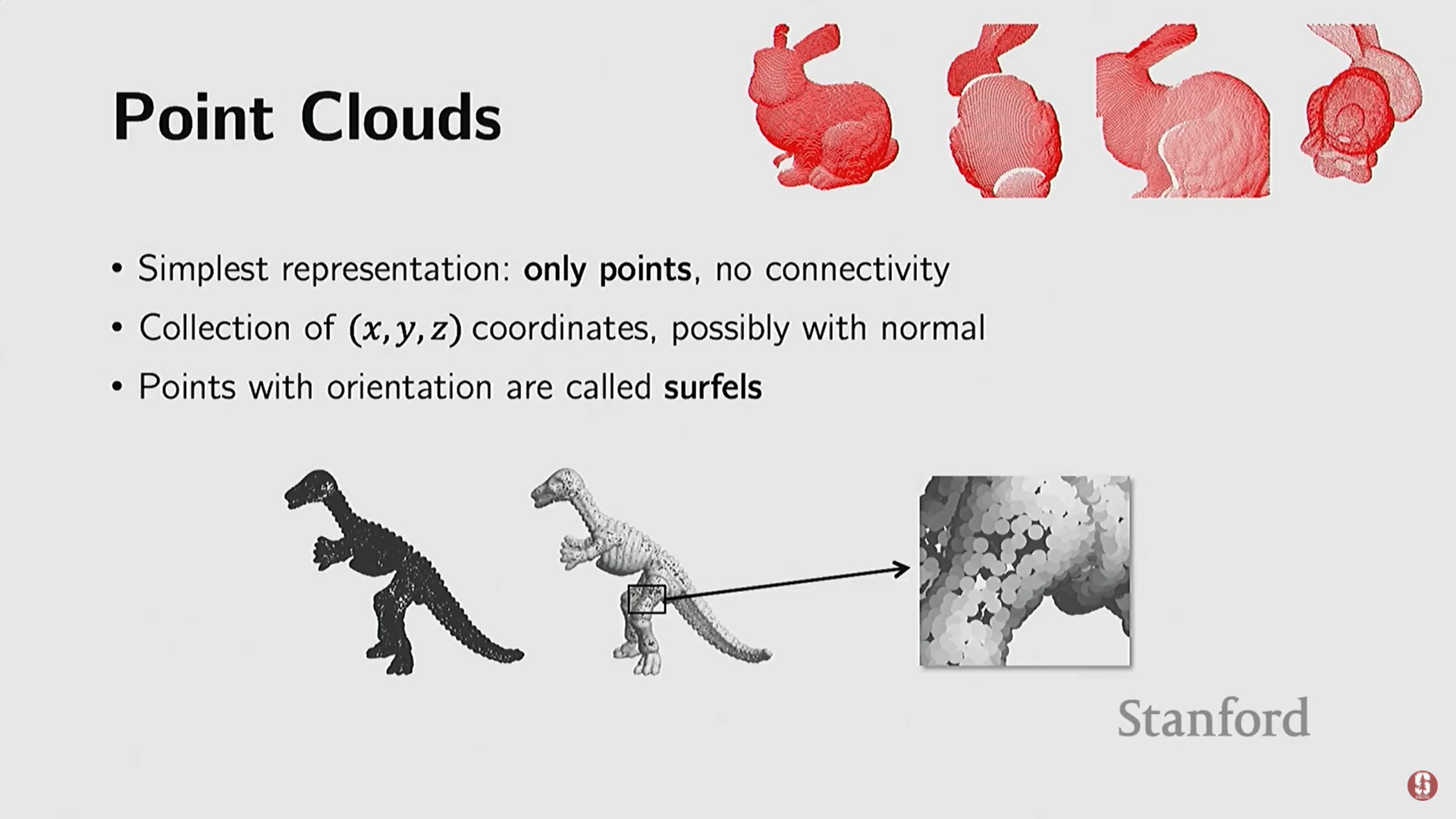
가장 단순한 표현 방식이며, 3D 공간의 점들만으로 구성된다.
특징: 점들 간의 연결성(connectivity) 정보가 없다.
저장: 픽셀처럼 행렬이 아닌, 각 점의 XYZ 좌표를 담은 $3 \times N$ 행렬로 저장된다 (N은 점의 개수).
추가 정보: 때로는 점의 표면 법선(surface normals) 정보를 포함하여 점이 향하는 방향을 나타내기도 한다 (이를 Surf라고 부른다). 법선은 렌더링 시 광원과의 상호작용을 고려하여 사실적으로 보이게 하는 데 필수적이다.
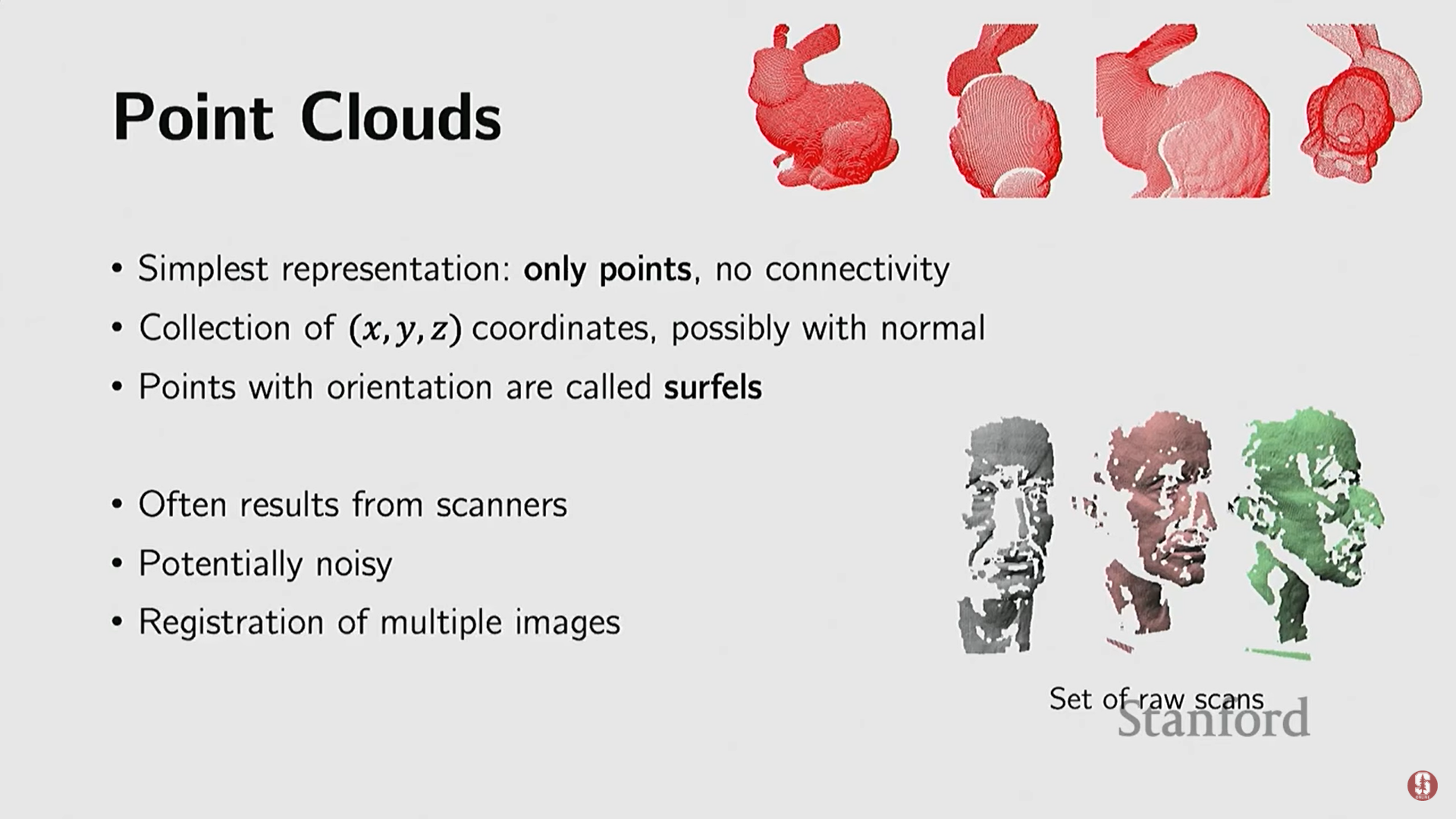
수집: 3D 스캐너나 깊이 센서, 심지어 iPhone의 AR Kit 같은 소프트웨어의 원시 출력(raw format) 형태로 자주 얻어진다.
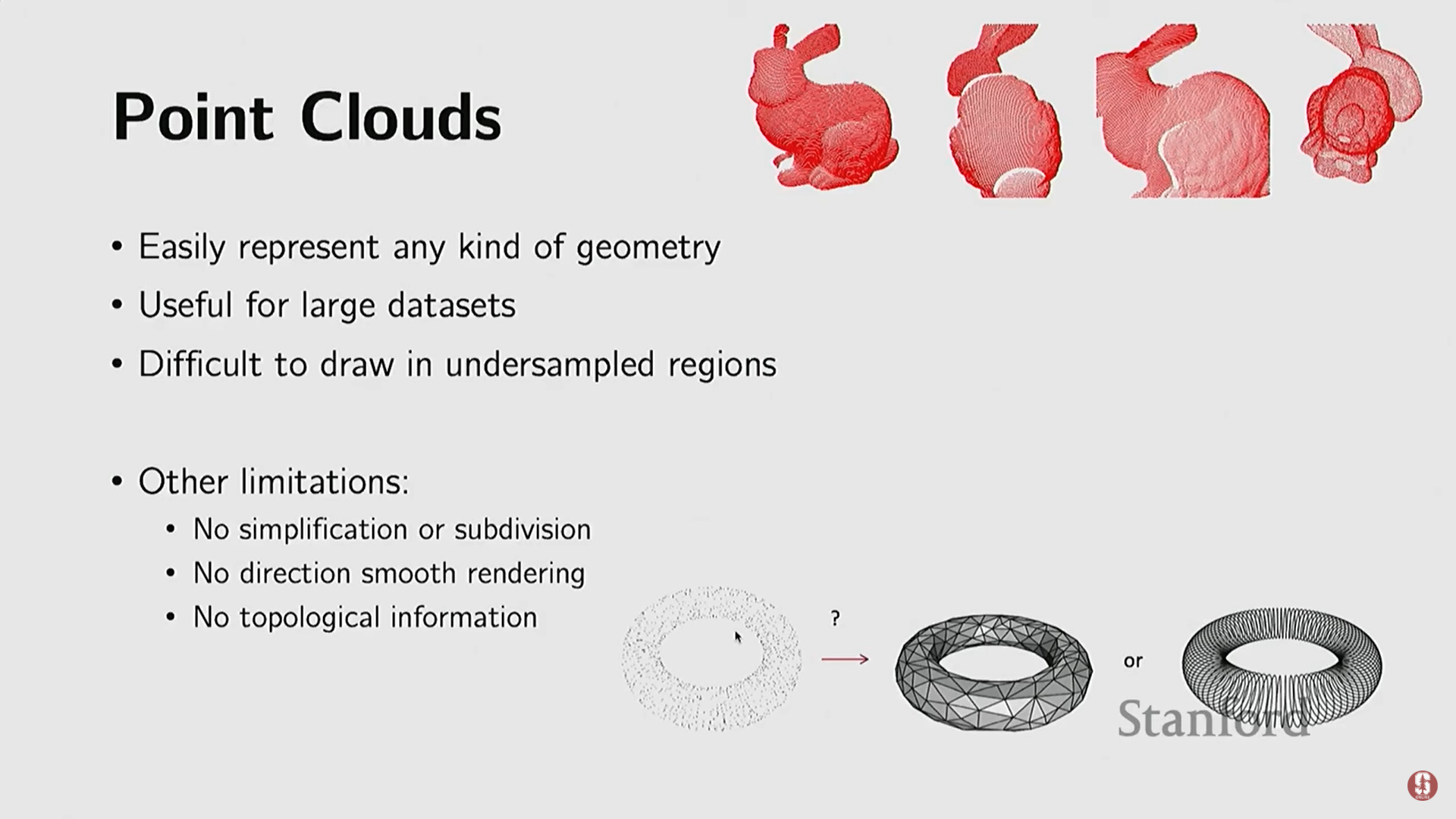
유연성: 위상(topology)에 제약을 받지 않아 어떤 객체 기하학도 표현할 수 있으며, 대규모 데이터셋에 유용하다.
한계점:
- 불규칙성: 점들이 균일하지 않게 샘플링될 경우 문제가 발생한다 (예: 토끼 머리는 많고 꼬리는 적은 경우).
- 연산의 어려움: 단순화(simplification)나 세분화(subdivisions) 같은 유용한 연산을 직접 수행하기 어렵다.
- 위상 정보 부족: 점들이 어떻게 연결되어 있는지 모르기 때문에, 토러스(Taurus)와 같은 링 모양 객체를 구별하기 어렵다.

(2) 폴리곤 메시 (Polygonal Meshes)

점들의 집합과 더불어 점들 간의 연결성(connectivity)을 포함하여 면(faces)과 표면(surfaces)을 표현한다.
활용: 그래픽 엔진 및 컴퓨터 게임에서 3D 객체를 표현하는 가장 널리 사용되는 방식이다.
복잡성: raw 메쉬의 경우 면마다 포함하는 점의 개수가 다를 수 있어 (3점, 4점 등), 특히 초기 신경망과의 통합에 큰 도전이었다.
규모: 수백만 개의 삼각형으로 조각상 디테일을 캡처하거나 (예: 5,600만 개의 삼각형), Google Earth처럼 수조 개의 삼각형으로 지구상의 모든 건물을 표현할 수 있다.
지원 연산:
- 세분화 (Subdivisions): 더 많은 메시를 사용하여 세부 정보를 추가한다.
- 단순화 (Simplification): 메시의 수를 줄여 빠르게 처리한다.
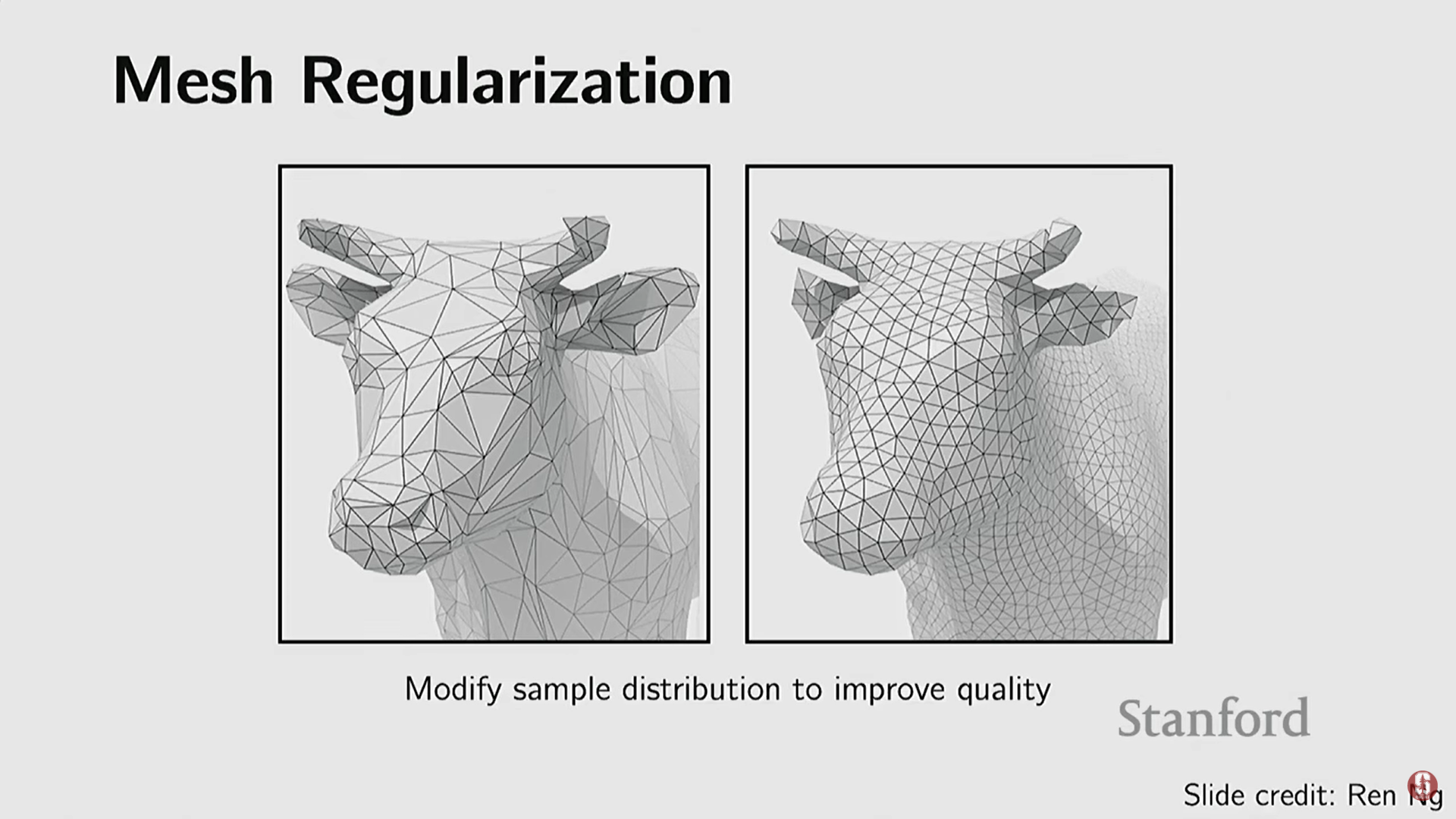
- 정규화 (Regularization): 불규칙한 메시를 처리하기 쉽도록 균일하게 만든다 (예: 모든 면을 삼각형으로 만들고 크기를 비슷하게 유지).

(3) 매개 변수적 표현 (Parametric Representations)

3D 객체를 함수로 표현하는 방식이다.
개념: 객체의 본질적인 내재된 차원(intrinsic dimensionality, 곡선의 경우 1D, 표면의 경우 2D)을 3D 공간으로 매핑하는 함수를 사용한다.
예시 (2D 곡선): 원을 점들의 집합 대신 하나의 함수로 표현할 수 있다. 변수 $t$ (각도) 하나를 변화시켜 원 위의 모든 점을 매핑한다.
$f(t) = (R \cos(t), R \sin(t))$
예시 (3D 구): 구는 두 개의 자유도( $U$ 와 $V$ )를 갖는 함수를 통해 3D 공간의 모든 점에 매핑될 수 있다.
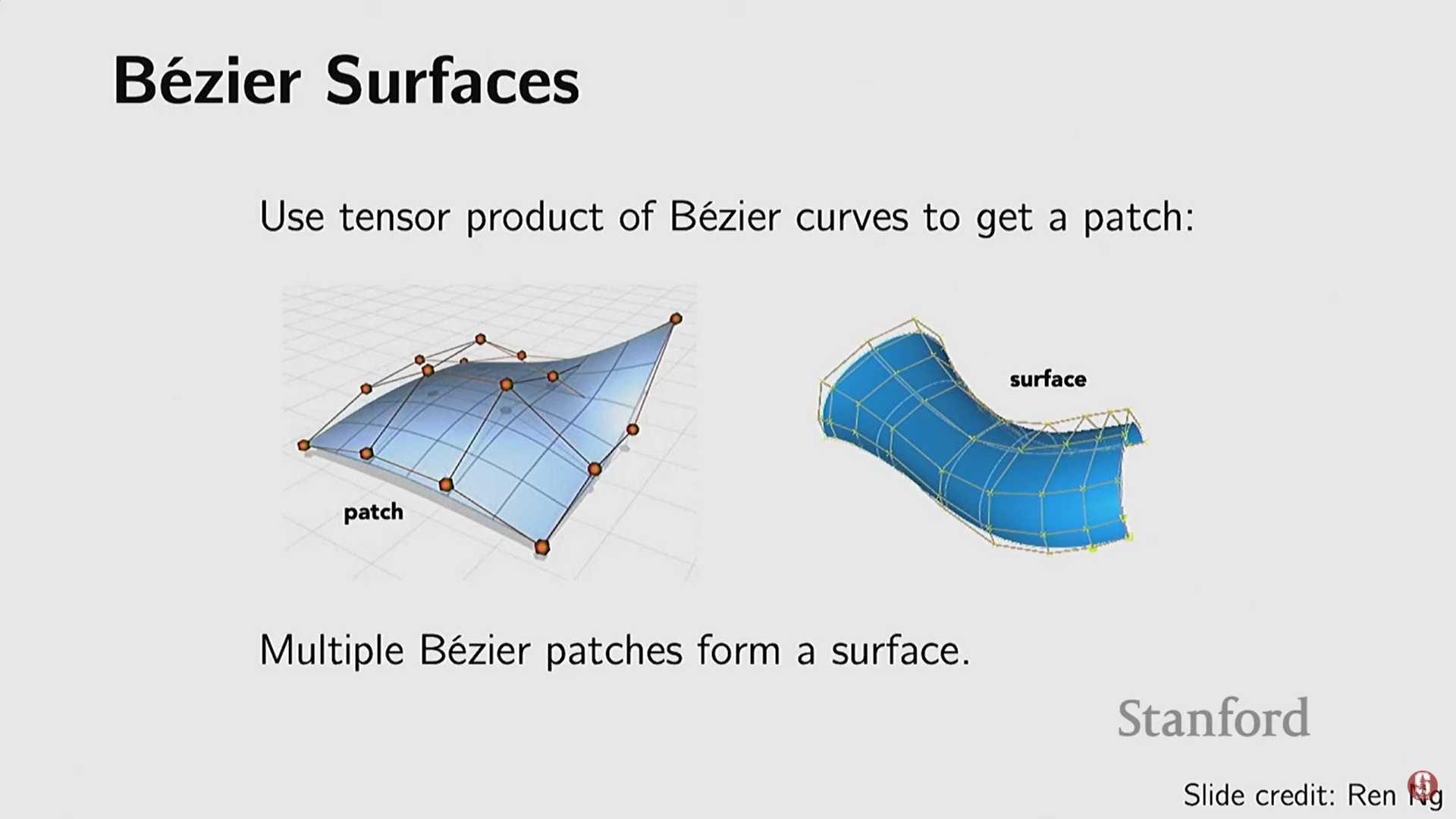
고급 방식: 몇 개의 제어점(control points)을 사용하여 유연하고 부드러운 표면을 표현할 수 있는 베지어 곡선(Bezier curves) 및 베지어 표면(Bezier surfaces)이 있다. 이는 세분화와 같은 연산을 지원한다.

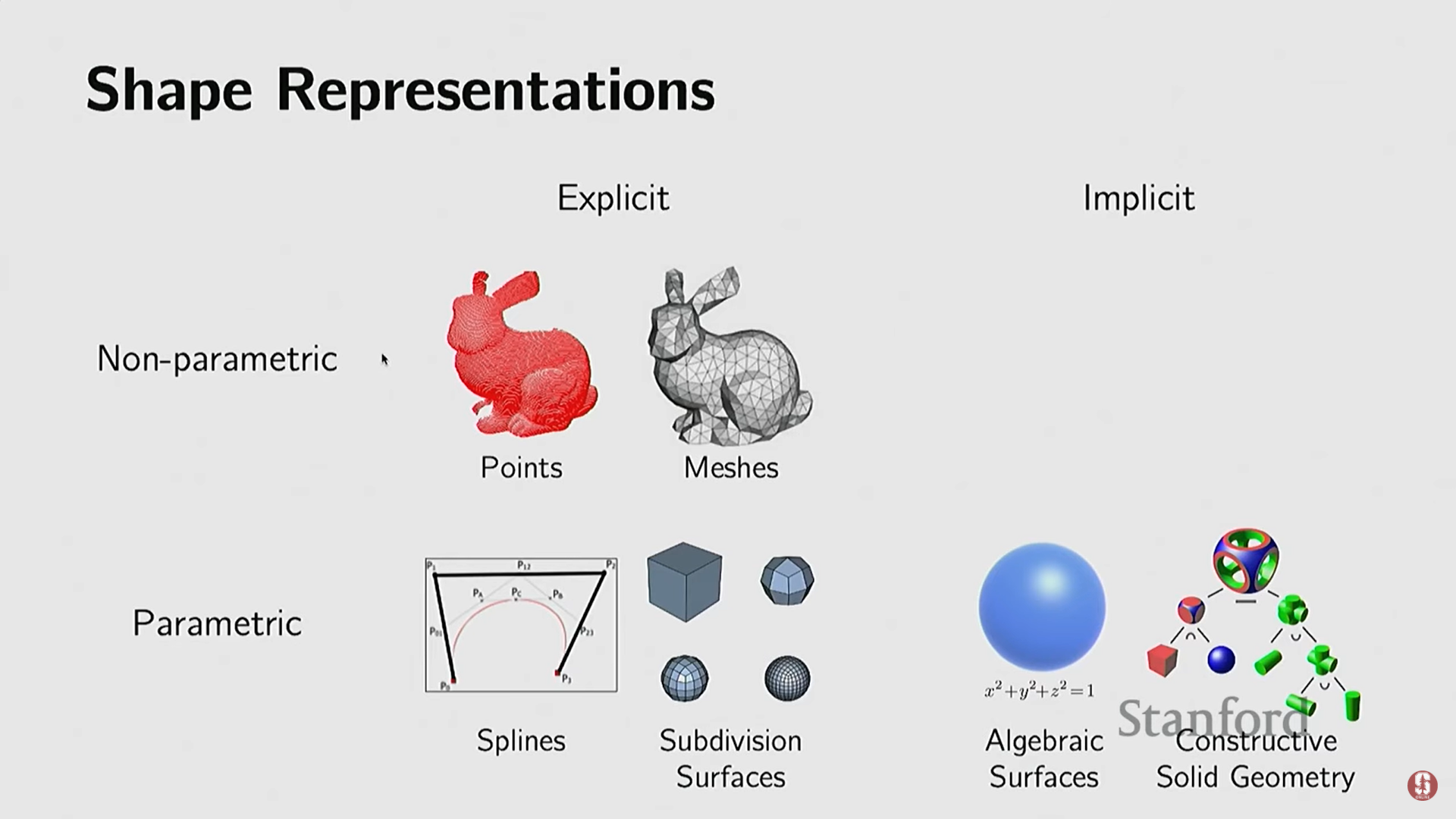
4) 암시적 표현 (Implicit Representations)

객체의 표면을 직접 정의하는 것이 아니라, 3D 공간의 점들이 특정 제약 조건(constraint)이나 함수를 만족하는지 여부로 객체를 정의하는 방식이다.
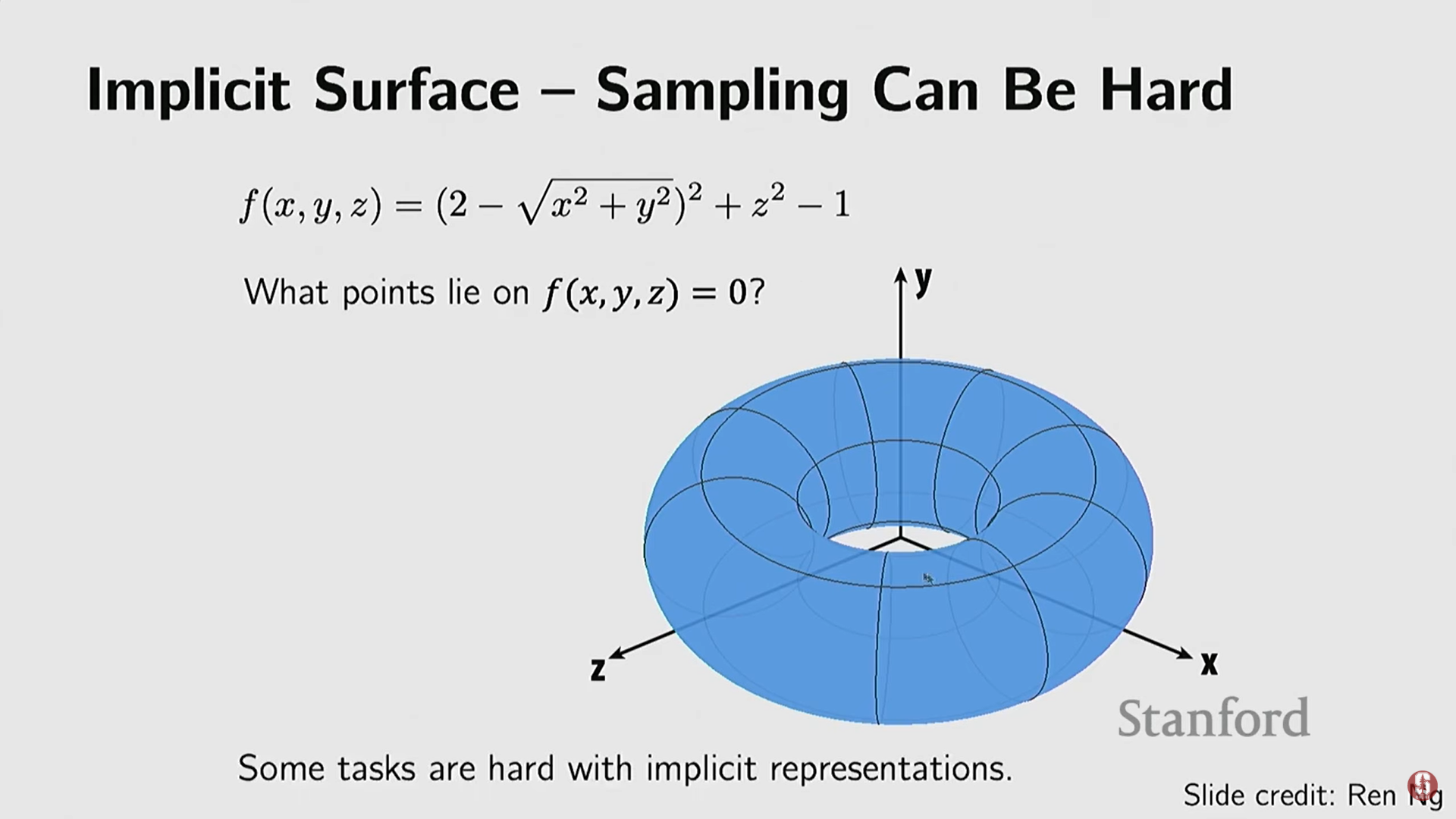
수학적 개념: 객체 표면 위의 점들은 $f(x, y, z) = 0$ 이라는 관계를 만족한다고 가정한다.
- 예시 (단위 구): 구 위의 모든 점은 다음 조건을 만족한다: $x^2 + y^2 + z^2 = 1 \quad \implies \quad f(x, y, z) = x^2 + y^2 + z^2 - 1 = 0$
구현: 복잡한 모양의 경우 폐쇄형(closed form) 함수를 작성하기 어렵기 때문에, 종종 뉴럴 네트워크(Neural Network)를 사용하여 이 함수 $f$ 를 표현한다.
적용 범위: 처음에는 기하학(Geometry) 표현에 사용되었으나, 나중에는 3D 객체의 색상, 외관(appearance), 재질 등까지 확장되었다.
장점:
- Inside/Outside 테스트의 용이성: 특정 쿼리 지점 $(x, y, z)$ 를 함수 $f$ 에 넣었을 때, 그 값의 부호로 내부/외부를 즉시 판단할 수 있다.
  - $f(x, y, z) < 0$ : 점은 객체 내부.
  - $f(x, y, z) > 0$ : 점은 객체 외부.
  - $f(x, y, z) = 0$ : 점은 객체 표면.
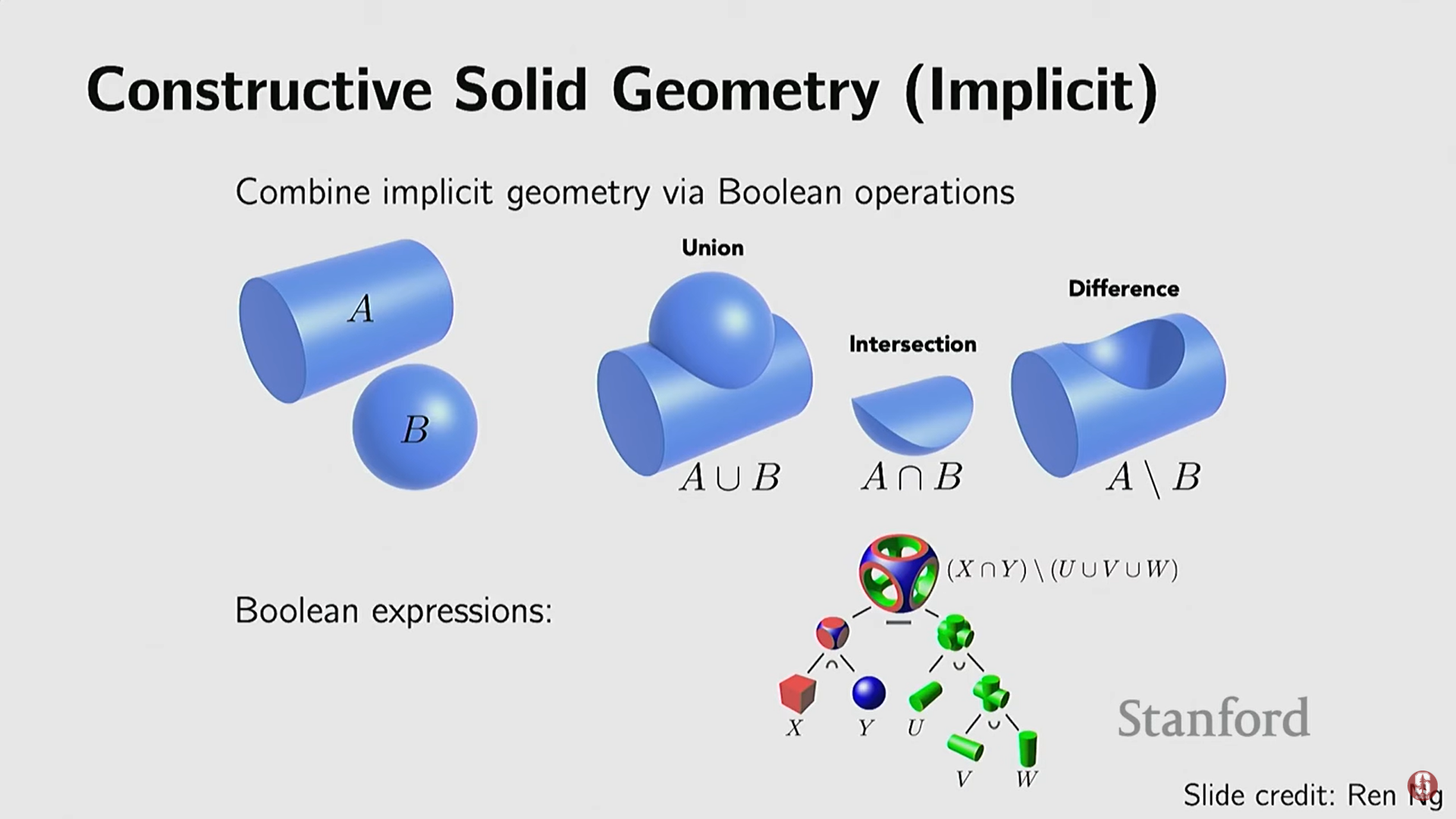
- 구성 및 결합 용이성: 논리 연산(합집합, 교집합, 차집합) 또는 산술 연산을 통해 여러 암시적 함수를 쉽게 결합하여 복잡한 모양을 만들 수 있다. 이는 산업 디자인(CAD 모델)에서 중요한 역할을 한다.
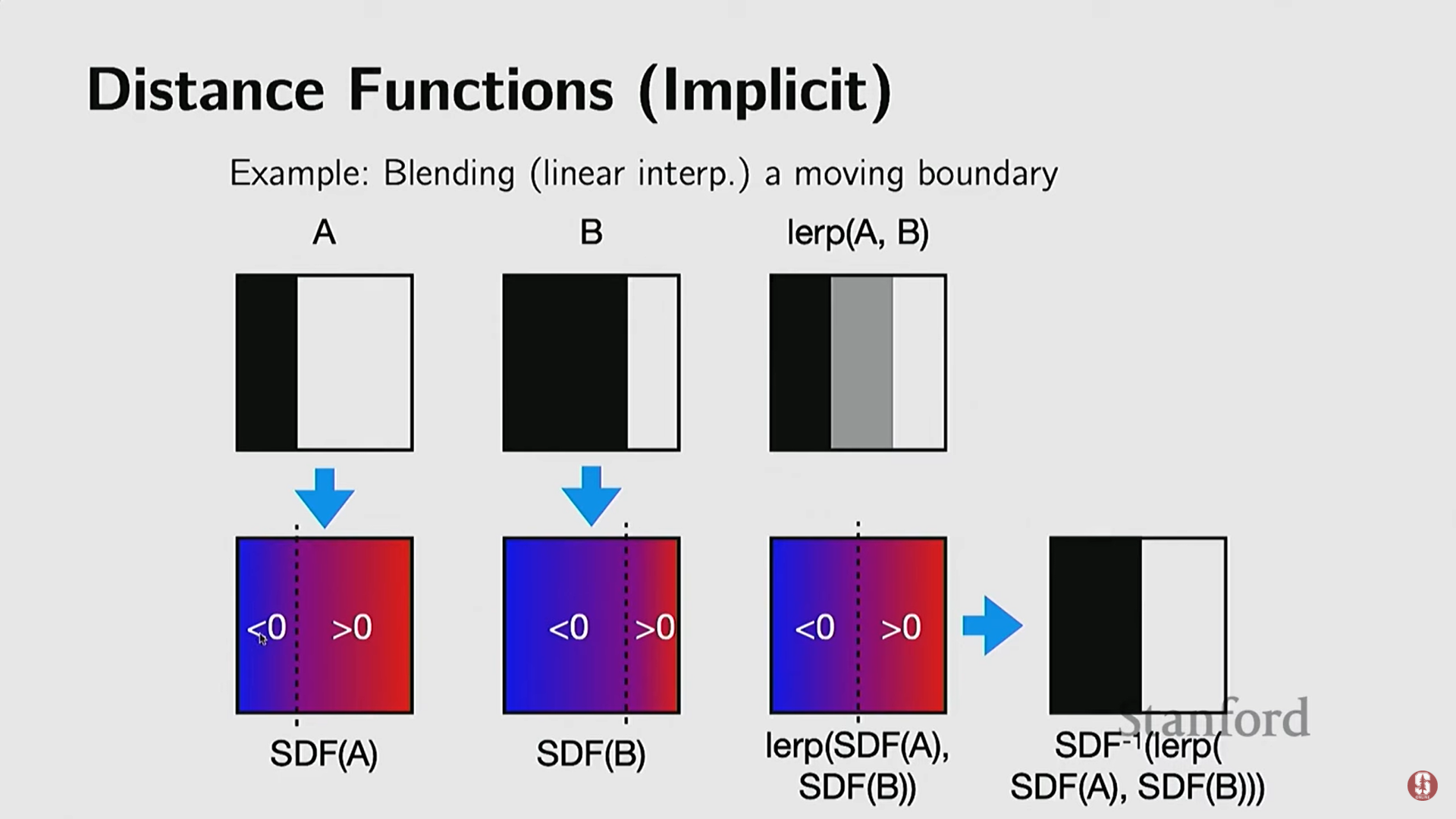
- 부드러운 블렌딩: 특히 거리 함수(Distance Function) (점과 표면 사이의 거리)를 사용할 경우, 이 함수들을 더함으로써 모양을 부드럽게 혼합할 수 있다.
단점:
- 샘플링의 어려움: 객체 표면 위의 점들을 $(x, y, z)$ 쌍으로 얻으려면 $f(x, y, z) = 0$ 방정식을 풀어야 하는데, 이 함수가 복잡할 경우 샘플링이 매우 어렵다.

5) 비매개 변수적 암시적 표현 (Nonparametric Implicit Representations)

암시적 함수를 사용하지만, 미리 쿼리하여 행렬에 값을 저장함으로써 비매개 변수적(nonparametric)이고 명시적인 제어를 가능하게 한다.

(1) 레벨 셋 (Level Sets)

복잡한 모양( $f(x, y, z)=0$ 의 폐쇄형이 없는 경우)의 경우, 3D 공간에 $100 \times 100 \times 100$ 과 같은 격자를 샘플링하고, 각 격자점에서 객체 표면까지의 거리 함수 값을 미리 계산하여 저장한다.
이 3D 행렬을 통해 경계(boundary, 값이 양수에서 음수로 바뀌는 지점)를 찾음으로써 객체 표면을 확인할 수 있다.
CT, MRI와 같은 의료 데이터에서 많이 사용된다.

(2) 복셀 (Voxels)

레벨 셋에서 거리 함수 값(예: +5, -5) 대신, 해당 점이 객체 내부에 있는지 외부에 있는지만을 이진화(binarize)하여 1 또는 0으로 저장한 3D 행렬이다.
특징: 픽셀(2D 행렬)의 3D 버전으로, 개념적으로 가장 이해하기 쉬운 표현이다.
딥러닝과의 연결: 딥러닝 초기(2012년 이후)에 컴퓨터 비전 연구자들은 2D CNN을 3D 데이터에 적용하기 위해 3D 행렬인 복셀을 가장 먼저 선택했다. 이는 2D 컨볼루션을 3D 컨볼루션으로 간단히 변경할 수 있다는 아날로지 때문이다.
한계점: 그래픽스 전문가들은 복셀이 계산이 느리고(미리 샘플링해야 함) 메쉬나 포인트 클라우드에 비해 품질이 낮다고 지적했다.

3. 딥러닝과 3D 비전의 통합

1) 초기 데이터셋과 발전 배경

초기 데이터셋: 딥러닝 이전에는 Princeton Data Shape Benchmark가 주로 사용되었으나, 180개 카테고리에 1,800개 모델로 매우 작았다.
ImageNet 효과: ImageNet처럼 대규모 3D 데이터셋의 필요성이 대두되었다.
- ShapeNet: Stanford 주도로 개발된 대규모 합성 데이터셋. 300만 개의 모델을 포함하며, 코어 데이터셋은 55개 카테고리, 5만 개의 모델로 구성된다. 이 데이터셋 덕분에 의자(Chairs)와 자동차(Cars)처럼 모델 수가 많은 카테고리에 대한 딥 네트워크 학습이 가능해졌다.
- Objaverse / Objaverse XL: 최근 AI2에서 수집된 더 크고 고품질이며 텍스처를 포함한 100만~1,000만 개의 3D 에셋 데이터셋.
실제 데이터셋의 도전:
- 3D 스캔 데이터셋 (Redwood, 2016).
- Meta/Oxford 등의 노력으로 iPhone 스캔을 통한 실제 객체 비디오 데이터셋 (약 19,000개 객체).
- 명확한 한계점: 3D 데이터셋의 규모(최대 10만 개 모델)는 2D 이미지 데이터셋(50억 개 이상)에 비해 여전히 엄청난 격차를 보인다.
구조화된 데이터셋: 객체의 부분(PartNet: 부품, 의미론, 이동성 정보) 및 3D 장면 데이터셋 (ScanNet: 1,500~3,000개 방)도 구축되었으나, 규모가 매우 작다.

2) 3D 비전의 주요 과제 (Tasks)

생성 모델링 (Generative Modeling): 3D 모양이나 장면 생성, 조건부 생성(언어/이미지 조건), 모양 사전 학습, 형상 복원(completion).
분류 모델링 (Discriminative Modeling): 3D 모양 분류 (의자, 테이블). 때로는 3D 객체를 2D 픽셀로 렌더링한 뒤 GPT와 같은 2D 모델을 활용하여 분류하기도 한다.
2D와 3D의 결합 모델링: 2D 파운데이션 모델(Foundation Models)의 현실성(realism) 사전 지식을 3D 재구성 작업에 활용하는 것이 중요해지고 있다.
뉴럴/차등 렌더링 (Neural/Differential Rendering): 3D 모델을 2D 픽셀로 변환하는 과정을 미분 가능하게(differentiable) 만들어 2D 데이터의 지식을 3D 세계로 전달할 수 있게 한다.

3) 딥러닝 초기 방법론

(1) 2D 뷰 기반 방법 (View-based Methods)

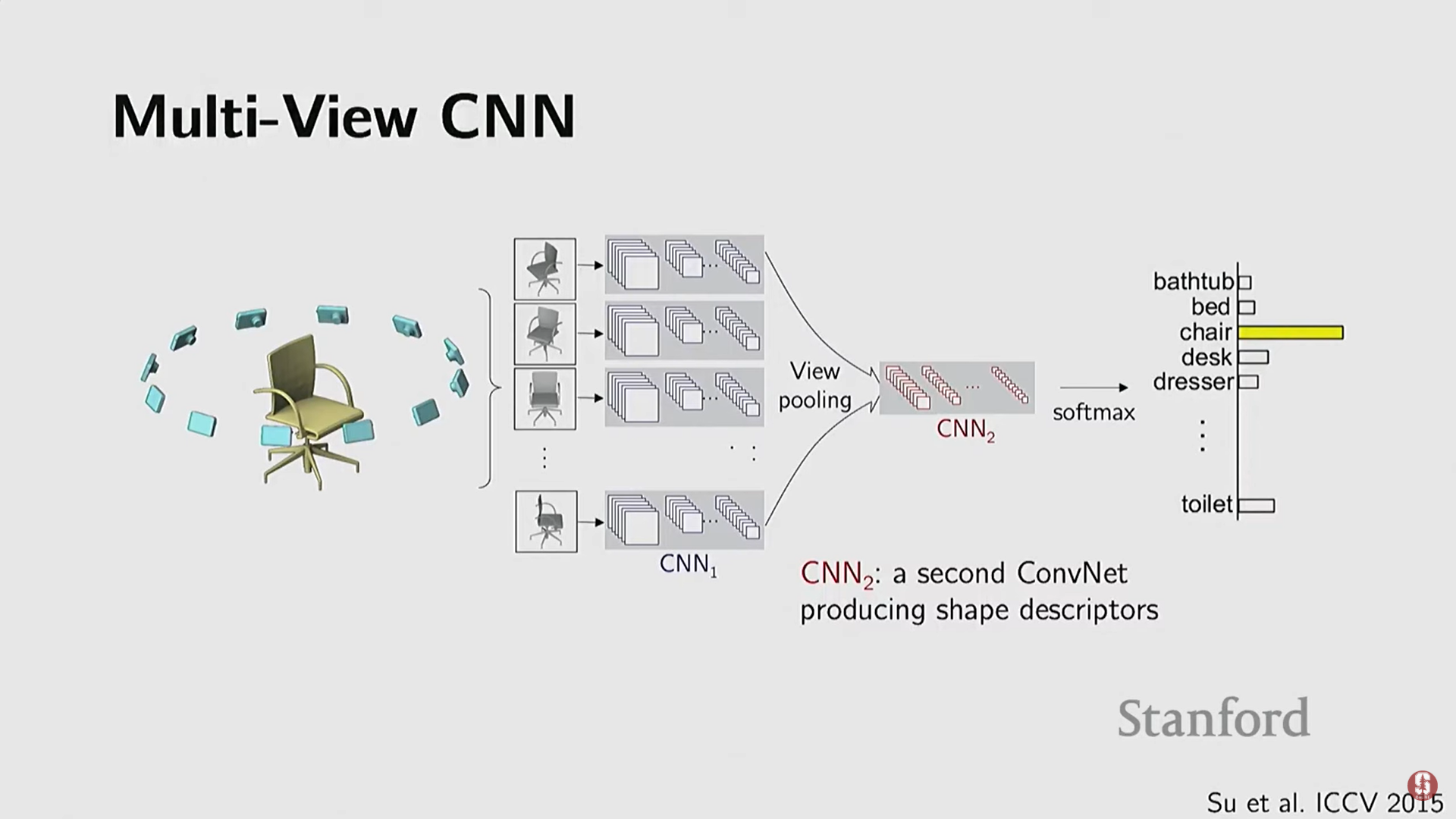
기술적 배경: 3D 네이티브 딥러닝 방법이 부재하던 초기(2012년 ImageNet 성공 후)에 시도된 아이디어.
작동 방식: 3D 객체를 여러 시점에서 2D 이미지로 렌더링하고, 이미 학습이 잘 된 2D CNN을 각 뷰에 적용한 뒤, 결과를 통합(Pooling 등)하여 분류한다.
장점: ImageNet으로 사전 학습된 2D 모델의 강력한 성능을 활용할 수 있다.
한계점: 노이즈가 많은 3D 입력의 경우 렌더링 품질이 떨어질 수 있으며, 3D 데이터를 2D로 투영하는 과정이 필요하다.

(2) 3D 네이티브 방법 (Volumetric CNNs)

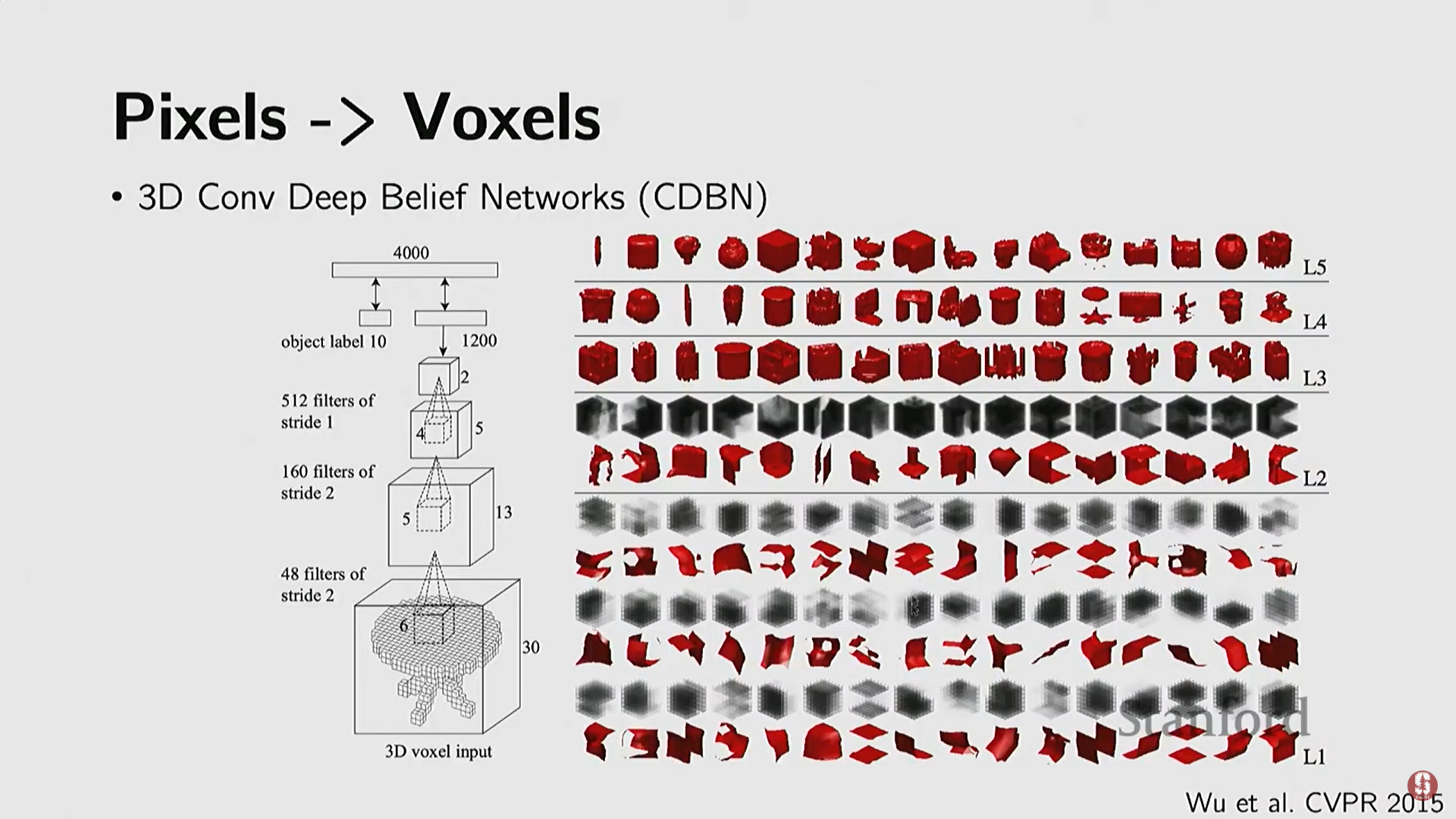
배경: 2D CNN의 성공을 3D 복셀로 확장하려는 시도.
3D 컨볼루션 (2015): Princeton 연구진은 3D 복셀 형태로 3D 모양을 합성할 수 있는 생성 모델(Deep Belief Network)을 학습시켰다.
3D 복셀 GANs (2016): 3D 복셀에 GAN(Generative Adversarial Networks)을 적용하여 3D 객체를 생성했다.
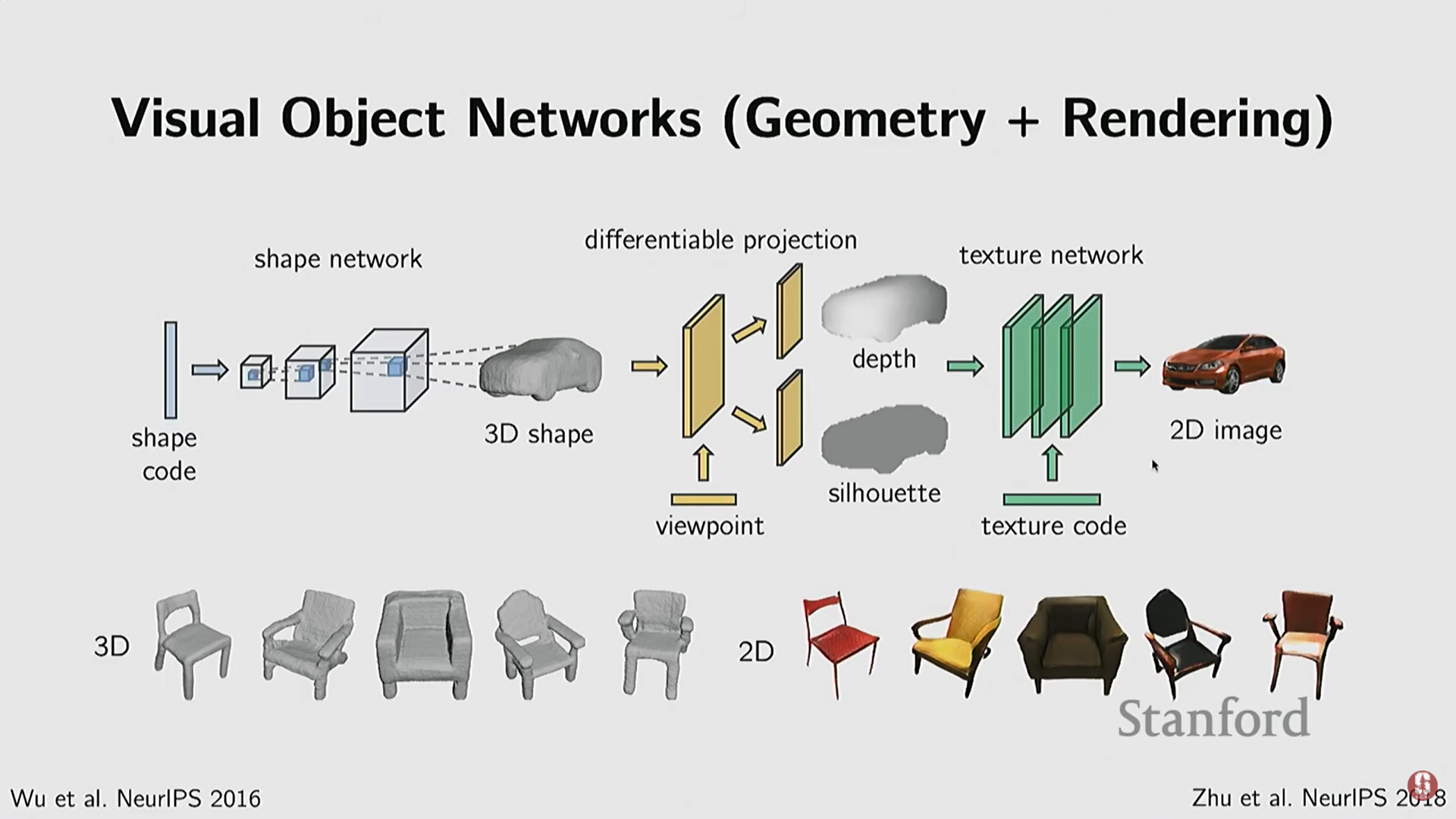
CycleGAN 확장 (2018): 3D 복셀 GAN의 결과를 2D 깊이 맵(depth map)으로 투영하고, CycleGAN을 이용해 이를 컬러 이미지로 변환하여 3D 모양과 2D 이미지 모두에서 적대적 손실(adversary losses)을 적용했다. 이를 통해 현실적인 3D 생성과 2D 렌더링을 동시에 수행하고 시점, 텍스처 등 제어 가능성을 확보했다.
옥트리 (OctTrees): 복셀의 비효율성을 개선하기 위한 방식. 공간을 재귀적으로 분할하며, 객체 표면에 가까운 영역은 더 미세한 해상도로, 빈 공간은 더 큰 복셀로 표현하여 공간 표현의 효율성을 높였다. 이를 통해 GPU 메모리에 더 높은 해상도( $256 \times 256$ vs $64 \times 64$ )의 객체를 담을 수 있게 되었다.

4) 불규칙 데이터 구조를 위한 딥러닝

(1) PointNet (포인트 클라우드)

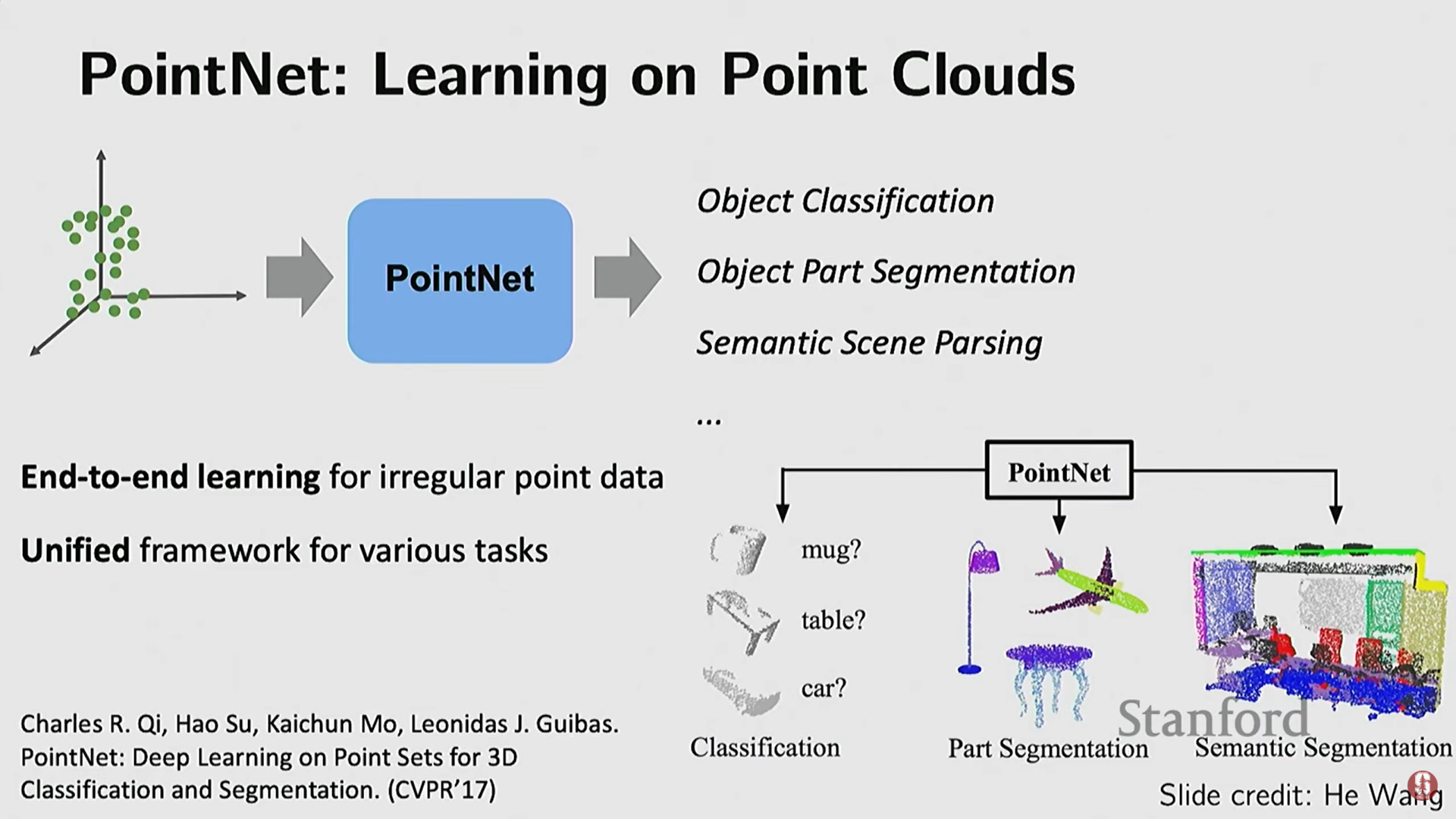
기술적 배경: 복셀의 비효율성과 낮은 품질 문제를 해결하고, 그래픽스에서 선호되는 포인트 클라우드를 직접 처리하기 위해 개발되었다.
핵심 요구사항:
- 순열 불변성 (Permutation Invariance): 점들의 입력 순서(예: $P_1, P_2$ vs $P_2, P_1$ )가 바뀌어도 네트워크의 결과는 같아야 한다. 포인트 클라우드는 순서가 없는(unordered) 데이터이기 때문이다.
- 샘플링 불변성 (Sampling Invariance): 객체의 다른 부분에서 샘플링된 점의 밀도가 달라져도 성능에 큰 영향을 받지 않아야 한다.
기술: 각 점의 임베딩을 계산한 후, 이를 결합하기 위해 대칭 함수(symmetric function)를 적용한다. 예: Max Pooling (각 차원별 최대값을 취함) 또는 합산(sum function). 이 단순한 아이디어가 순열 불변성을 보장하며 강력한 성능을 보였다.
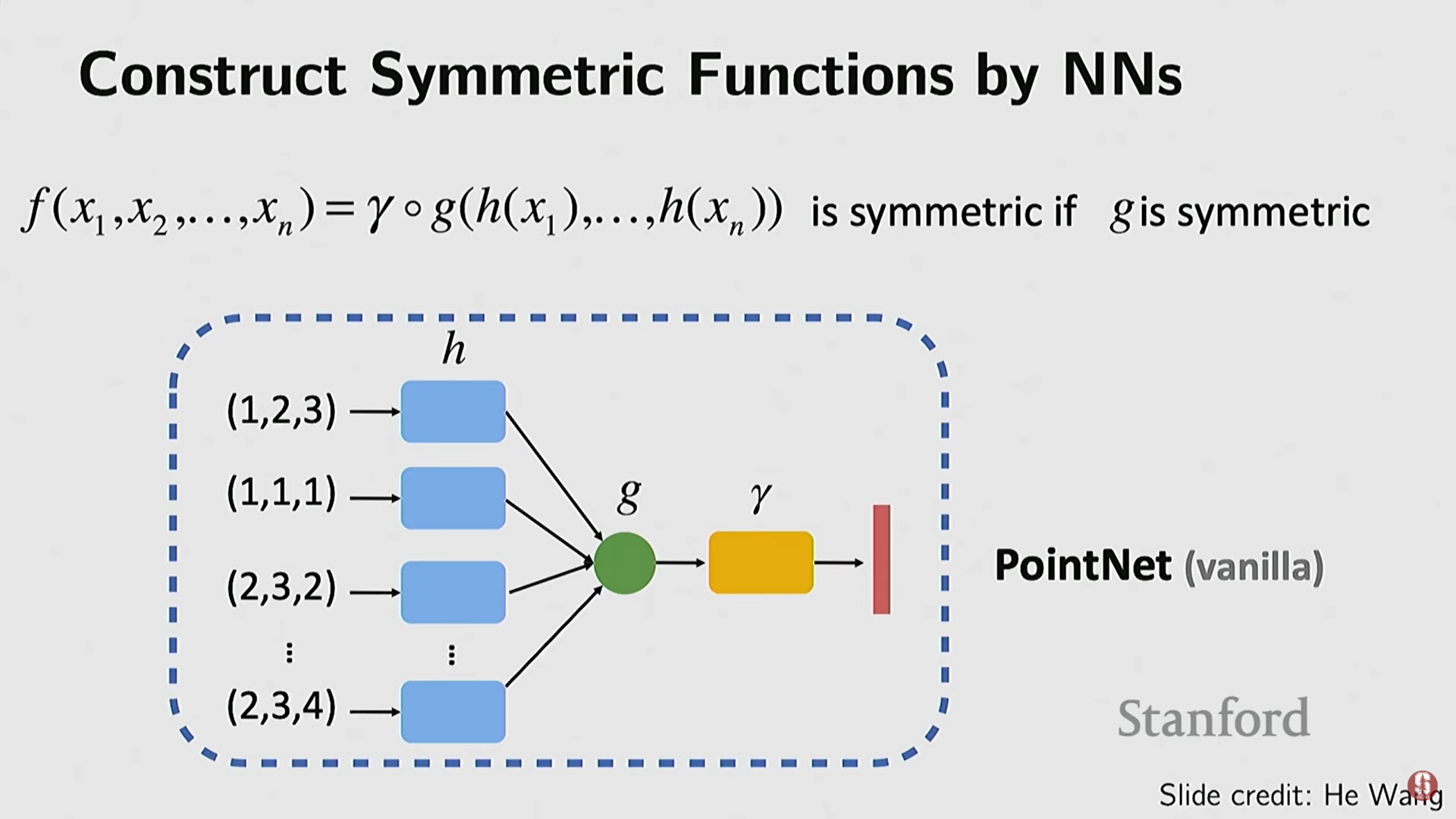
관련 발전: 포인트 클라우드를 그래프의 노드로 보고, 인접성을 엣지로 연결하는 그래프 신경망(Graph Neural Networks, GNNs) 방식도 개발되었다.
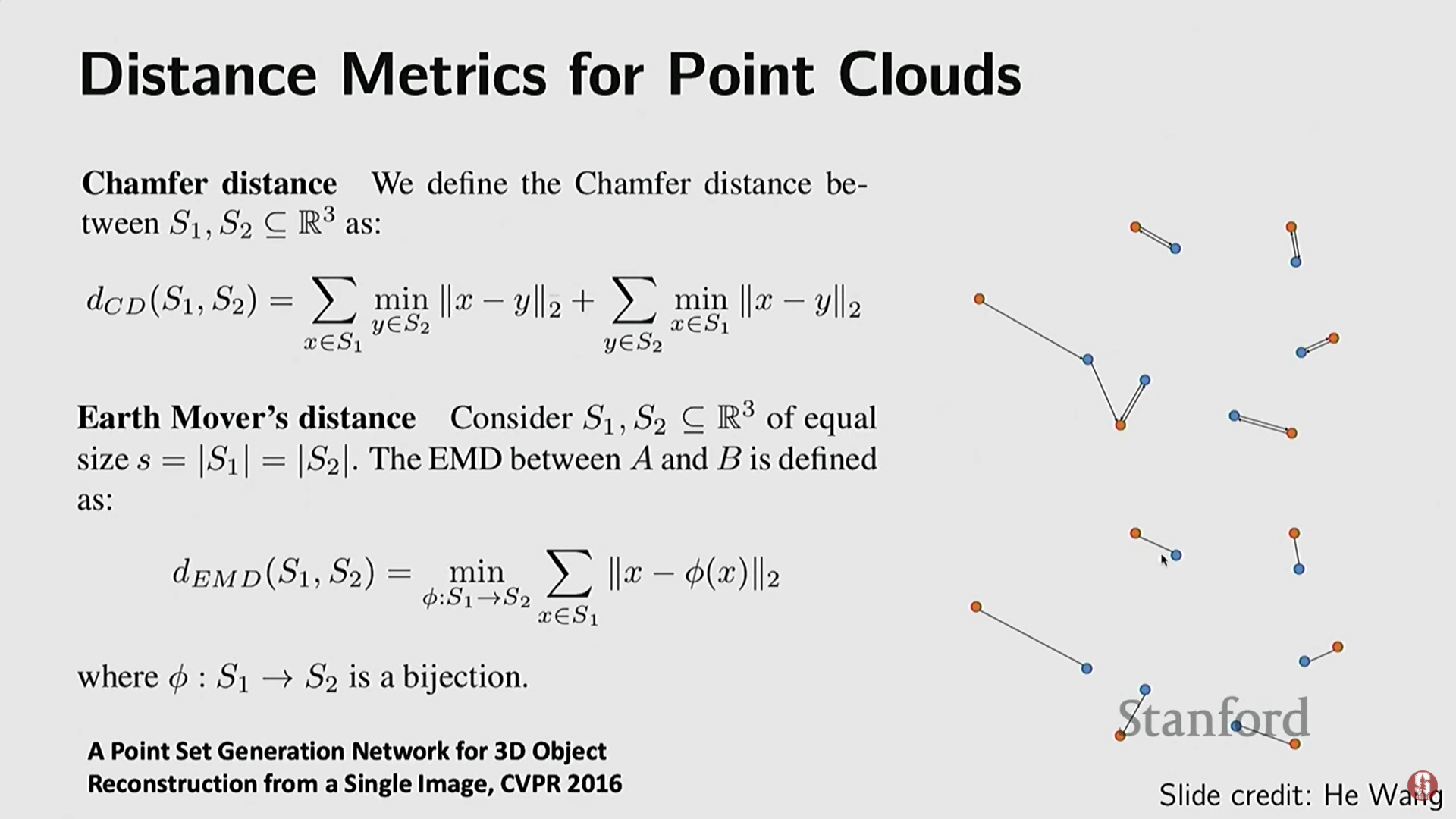
평가 지표 (손실 함수): 포인트 클라우드 생성 작업에서 출력된 점과 정답 점을 비교하기 위해 특별한 거리 측정 방식이 필요하다.
- 챔퍼 거리 (Chamfer Distance): 두 점 집합(빨간색, 파란색)이 있을 때, 각 집합의 점들이 상대편 집합에서 가장 가까운 이웃 점까지의 거리를 찾아 이를 최소화한다.
- 지구 이동 거리 (Earth Mover's Distance, EMD): 두 점 집합 사이에 일대일 이분 매칭(bipartite matching)을 수행하여 쌍으로 묶인 점들 간의 거리를 최소화한다. 이 지표들은 미분 가능하게 만들어져 신경망 최적화에 사용될 수 있다.

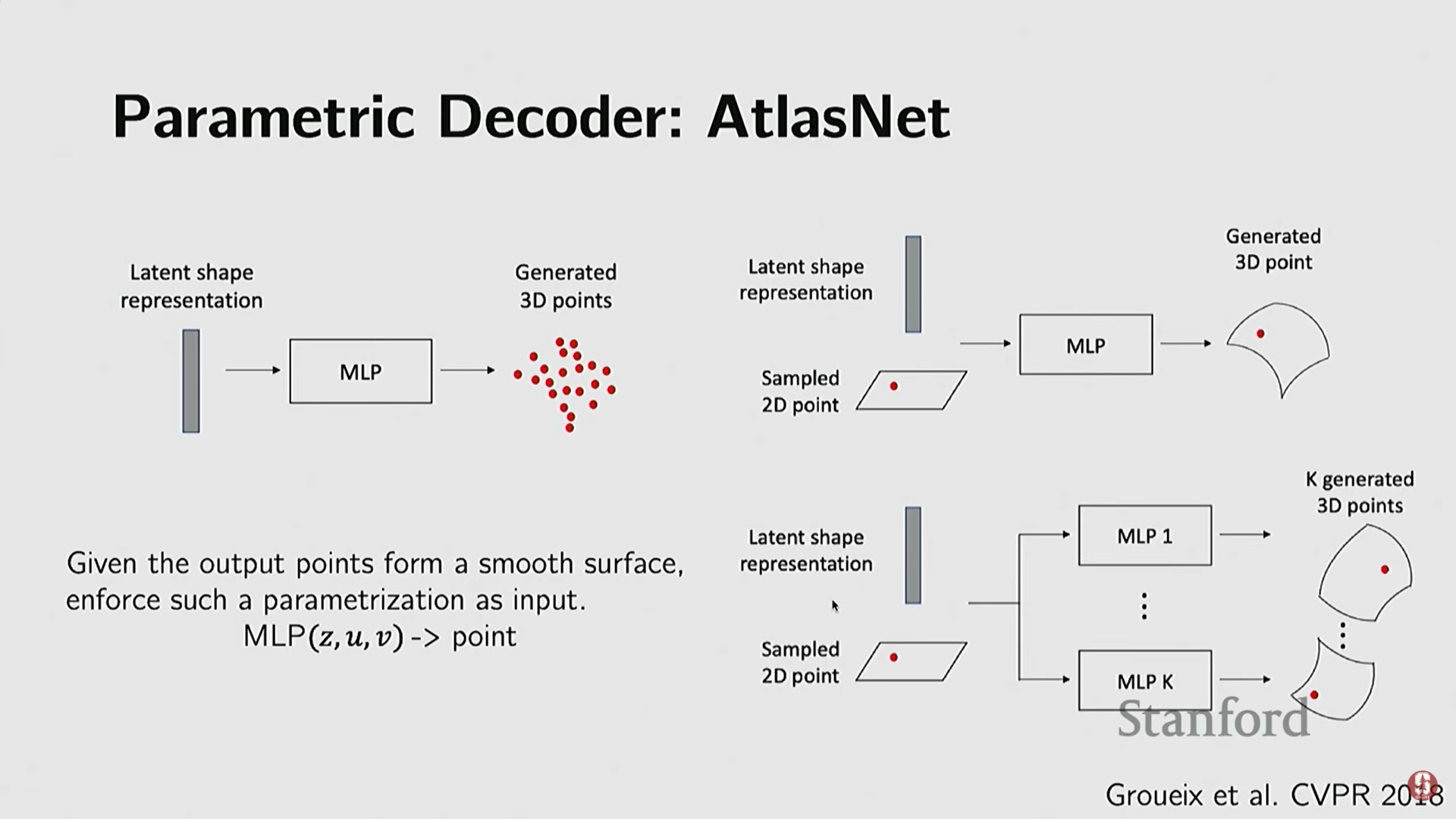
(2) AtlasNet (매개 변수적 곡면)

기술적 배경: 복셀이나 포인트 클라우드가 생성하는 표면의 매끄럽지 않음(smoothness) 문제를 해결하고, 스플라인(splines)과 같은 아름다운 곡면을 표현하기 위해 개발되었다.
작동 방식: 저차원 공간(예: 2D $U, V$ 평면)을 3D 공간으로 변환하는 복잡한 함수 $F$ 를 MLP(다층 퍼셉트론)와 같은 뉴럴 네트워크로 학습한다.
복합 구조: 전체 객체를 하나의 변환 함수로 표현하기 어려우므로, 여러 개의 작은 뉴럴 네트워크(마치 종잇조각을 접는 것처럼)를 사용하여 객체의 여러 부분을 변환하고 이를 합쳐 최종 모양을 만든다.
결과: 복셀이나 포인트 클라우드보다 훨씬 부드러운 표면을 재구성할 수 있다.

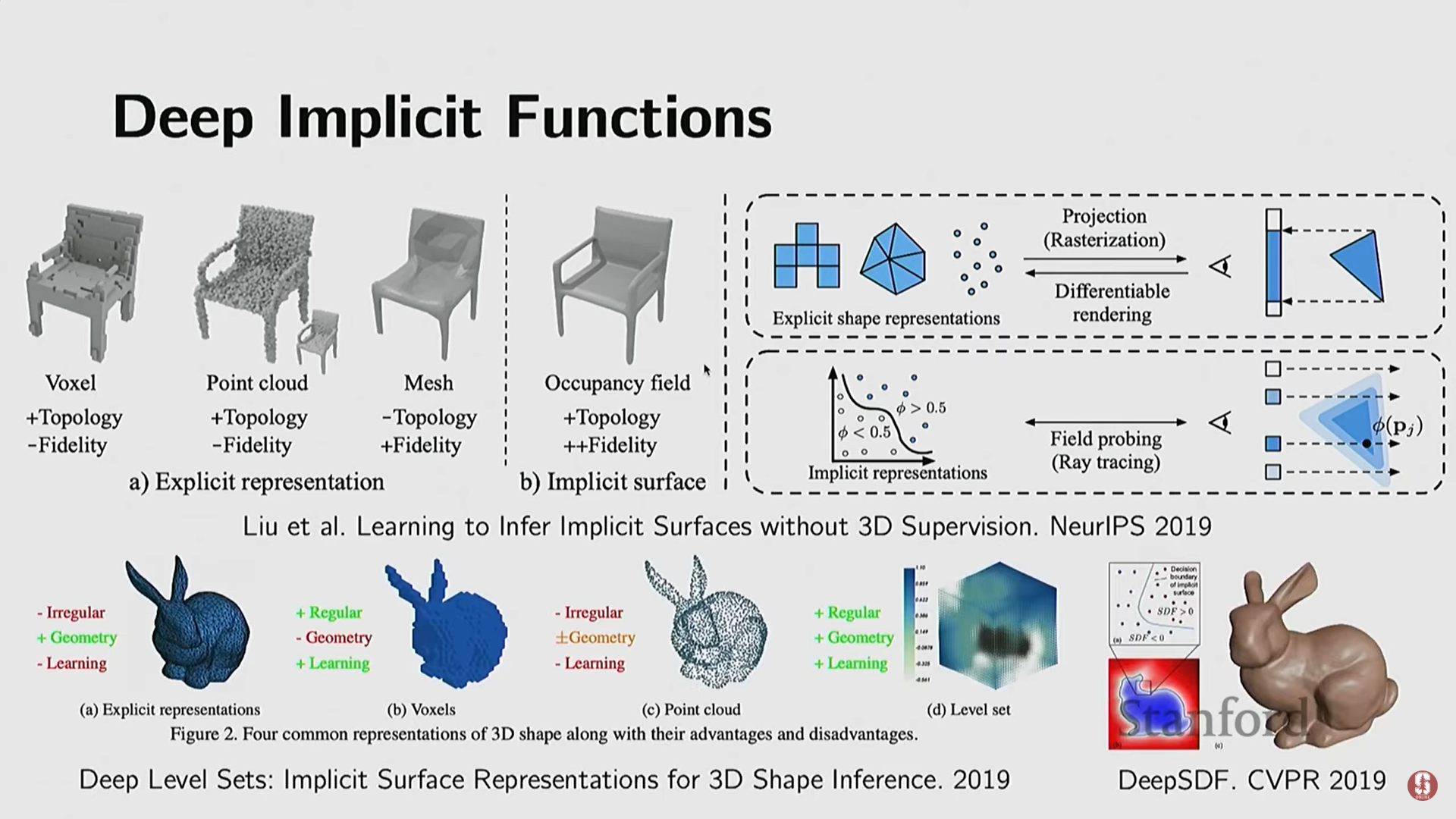
5) 암시적 함수 패러다임의 완성 (Implicit Functions)

새로운 패러다임 (2019): 딥 네트워크가 본질적으로 매우 복잡한 함수라는 점을 인식하고, 이를 3D 기하학을 표현하는 암시적 함수로 직접 사용하는 아이디어가 등장했다.
작동 방식: 3D 공간의 쿼리 지점(xyz 좌표)을 딥 네트워크에 입력하면, 네트워크는 해당 지점이 객체 내부에 있는지 외부에 있는지 (1차원 출력) 알려준다.
확장: 단순히 이진 분류(Inside/Outside)를 넘어, 점과 표면 사이의 부호 있는 거리 함수(Signed Distance Function, SDF) 값, 밀도(density) 값, 색상(color), 또는 복사 에너지(radiance) 값 등을 쿼리하도록 확장되었다.

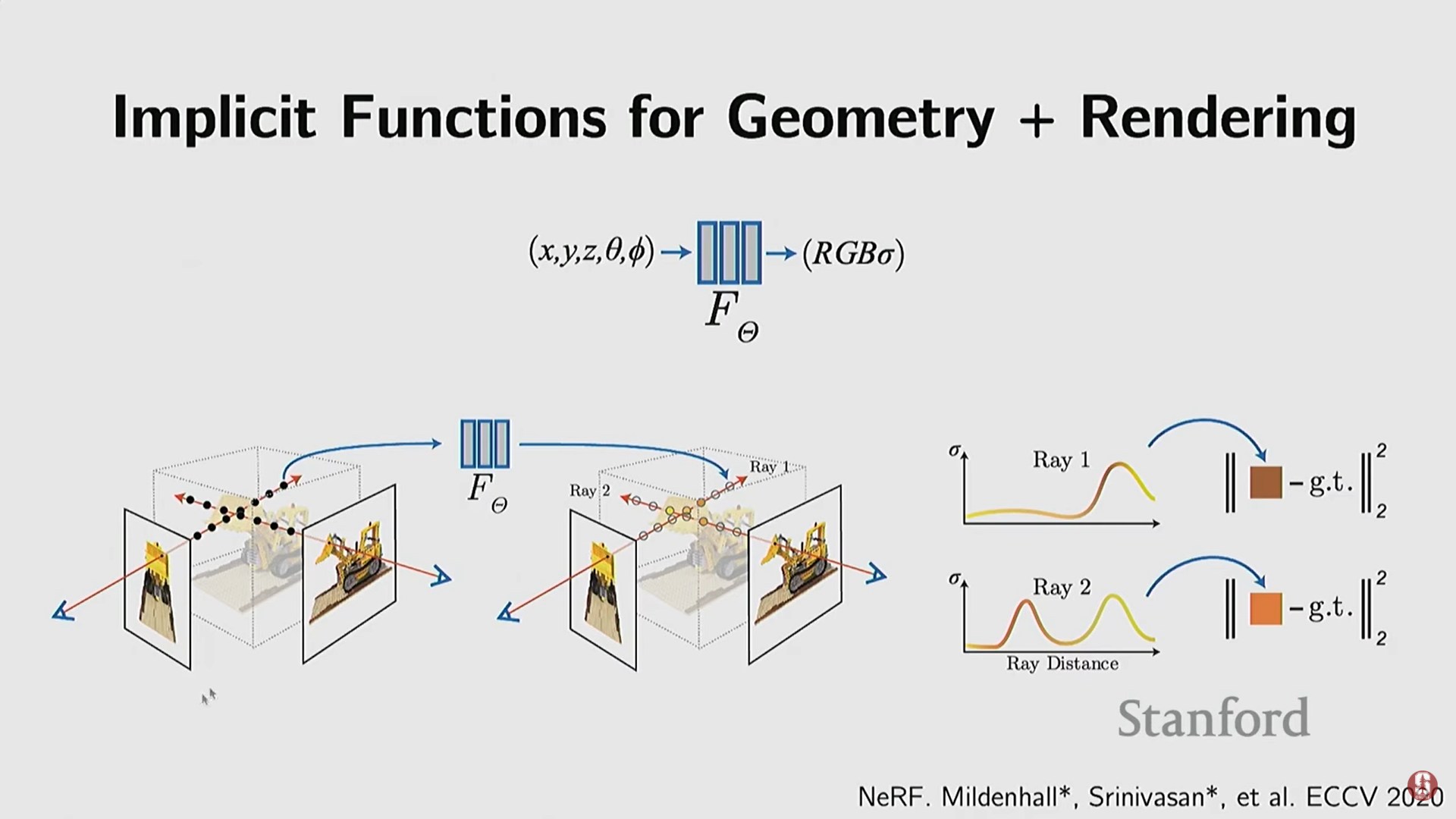
(1) NeRF (Neural Radiance Fields)

기술적 배경: 딥 암시적 함수(Deep SDF 등)에서 한 단계 발전하여, 기하학적 정보뿐만 아니라 외관(appearance) 정보까지 모델링했다.
입력 및 출력:
- 입력: 3D 공간 좌표 ( $x, y, z$ ) + 시야 방향(Viewing Directions).
- 출력: 해당 지점의 밀도(Density)와 색상/복사 에너지(Color/Radiance).
학습 방식 (핵심 변화):
- NeRF는 3D 기하학 정답(Supervision) 대신 2D 이미지로부터 직접 학습한다.
- 차등 볼륨 렌더링 (Differentiable Volume Rendering): NeRF는 컴퓨터 그래픽스의 볼륨 렌더링 공식을 사용하여 3D 필드(밀도 및 색상)를 2D 픽셀로 변환하는 과정을 미분 가능하게 구현했다. 이를 통해 신경망이 2D 이미지와 출력된 렌더링 이미지를 비교하여 역전파를 수행하며 3D 필드를 학습할 수 있다.
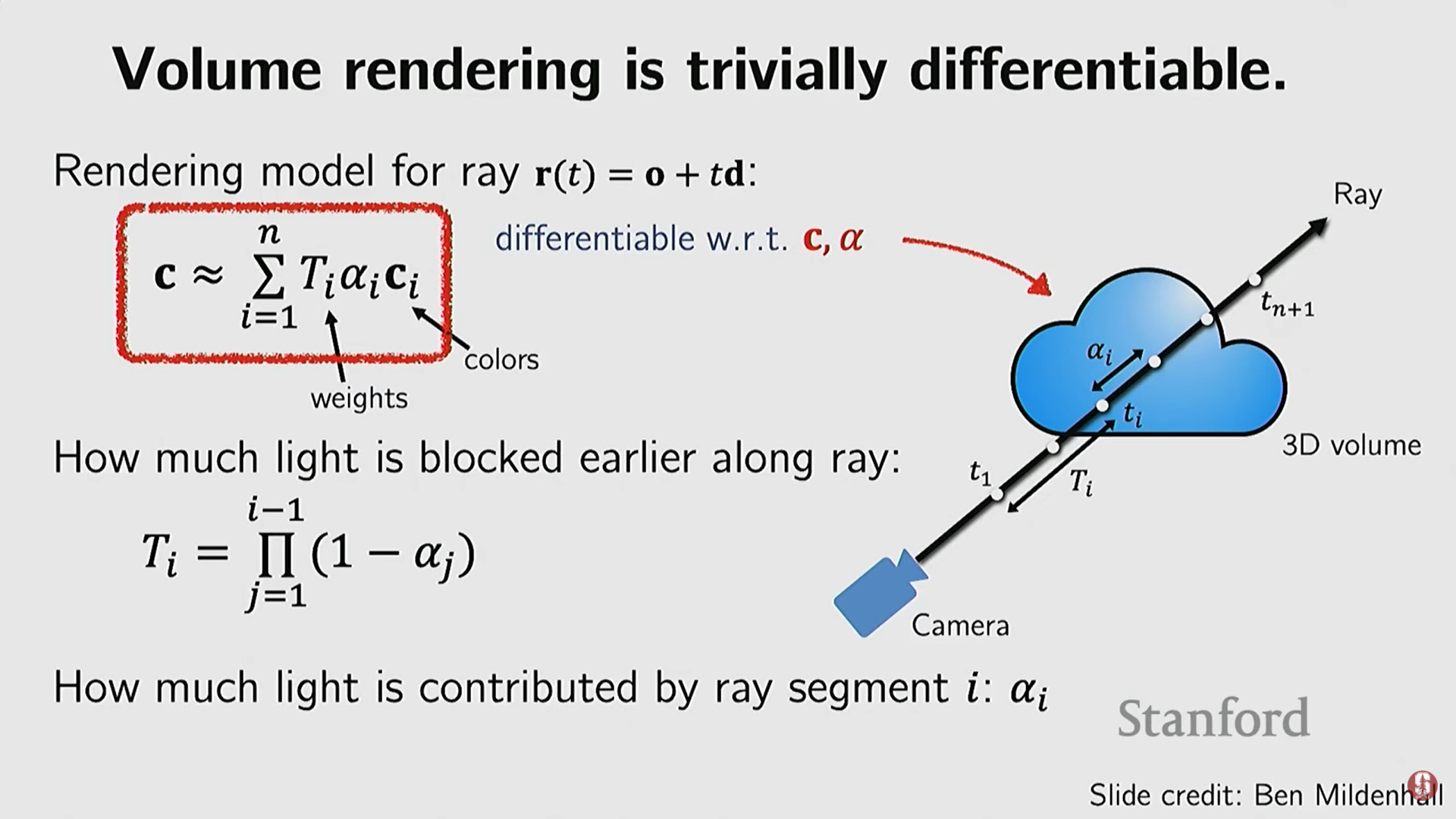
- 수학적 설명: 볼륨 렌더링 방정식을 통해 광선 경로를 따라 밀도(불투명도)와 색상 값이 어떻게 빛의 차단과 색상 기여에 영향을 미치는지 계산할 수 있다.
심화 내용:
- NeRF는 SDF 같은 초기 암시적 함수 연구에서 영감을 받았으나, 기하학과 외관을 결합하고 2D 이미지 학습을 가능하게 함으로써 큰 도약을 이루었다.
- PI-GAN: NeRF의 암시적 복사 필드를 생성 신경망(GAN) 프레임워크에 통합하여, 3D 객체와 2D 이미지를 동시에 사실적으로 생성하는 모델이다. 이미지로부터 직접 학습이 가능해 ShapeNet에 국한되지 않고 다양한 카테고리에서 사실적인 생성이 가능해졌다.

(2) NeRF의 한계점과 3D Gaussian Splatting

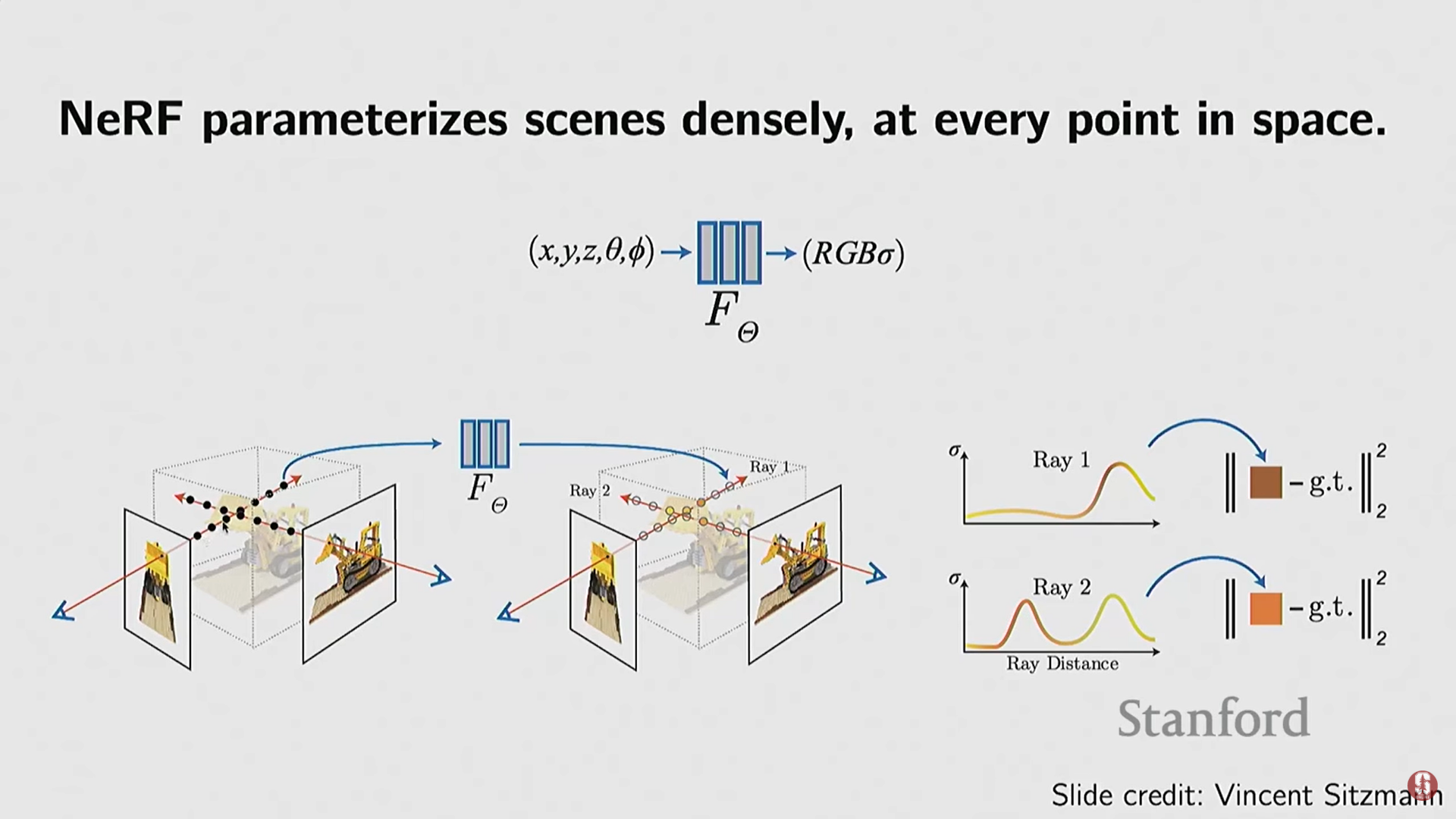
NeRF의 병목 현상: NeRF는 3D 공간을 매우 조밀하게(densely) 샘플링해야 하므로, 쿼리가 많아 계산 속도가 매우 느리다. 대부분의 샘플링은 빈 공간에 대한 쿼리이므로 컴퓨팅 파워가 낭비된다.
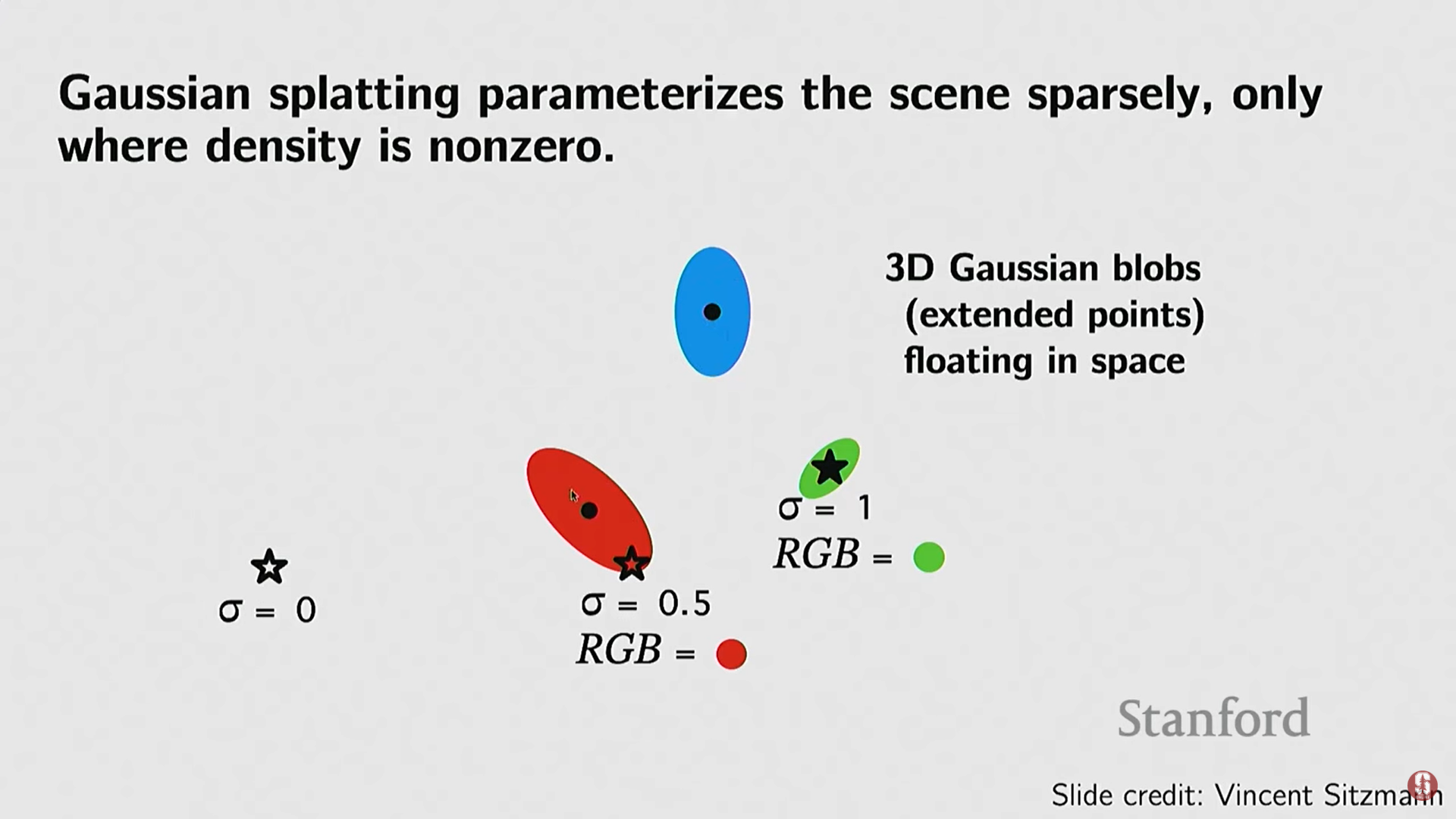
3D Gaussian Splatting (3DGS):
- 목표: 암시적 표현의 장점(고품질)과 명시적 표현의 효율성(희소성)을 결합하여 NeRF의 느린 속도를 개선한다.
- 기술: 장면을 조밀한 쿼리 대신, 3D 공간에 3D 가우시안 블롭(Gaussian blobs) (희소한 점 클라우드와 유사하지만 부피를 가짐)의 집합으로 표현한다.
- 효율성: 카메라 광선(ray)을 쏠 때, 블롭이 있는 영역에서만 샘플링을 수행하고 빈 공간의 쿼리를 피함으로써 렌더링 효율을 극대화한다.
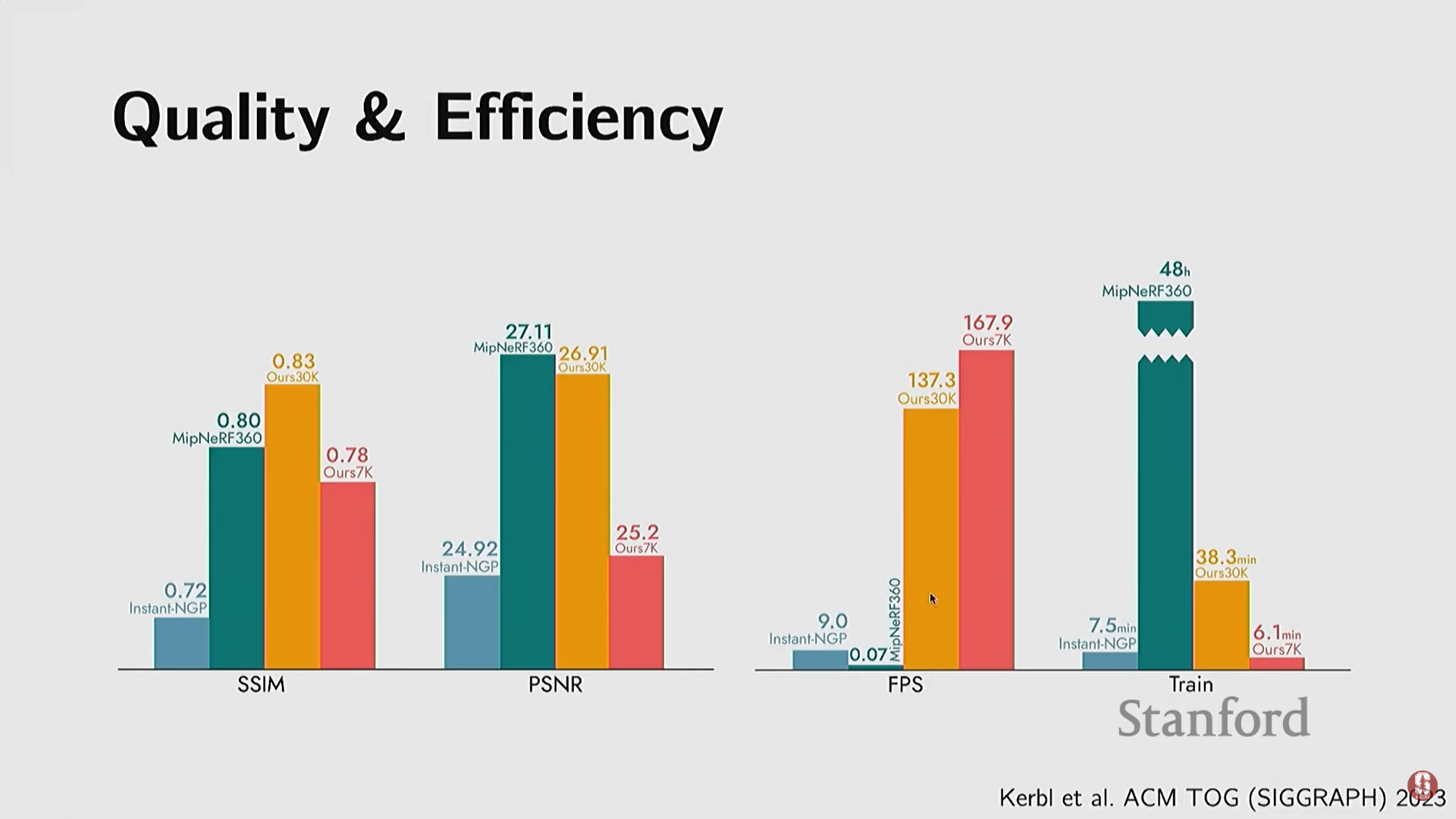
- 결과: 렌더링 품질은 NeRF와 유사하면서도, 렌더링 속도를 1,000배 이상 (예: 150 FPS vs. 단일 이미지 렌더링에 20초) 향상시켰다.

6) 구조적 및 프로그램적 표현 (Structural and Programmatic Representations)

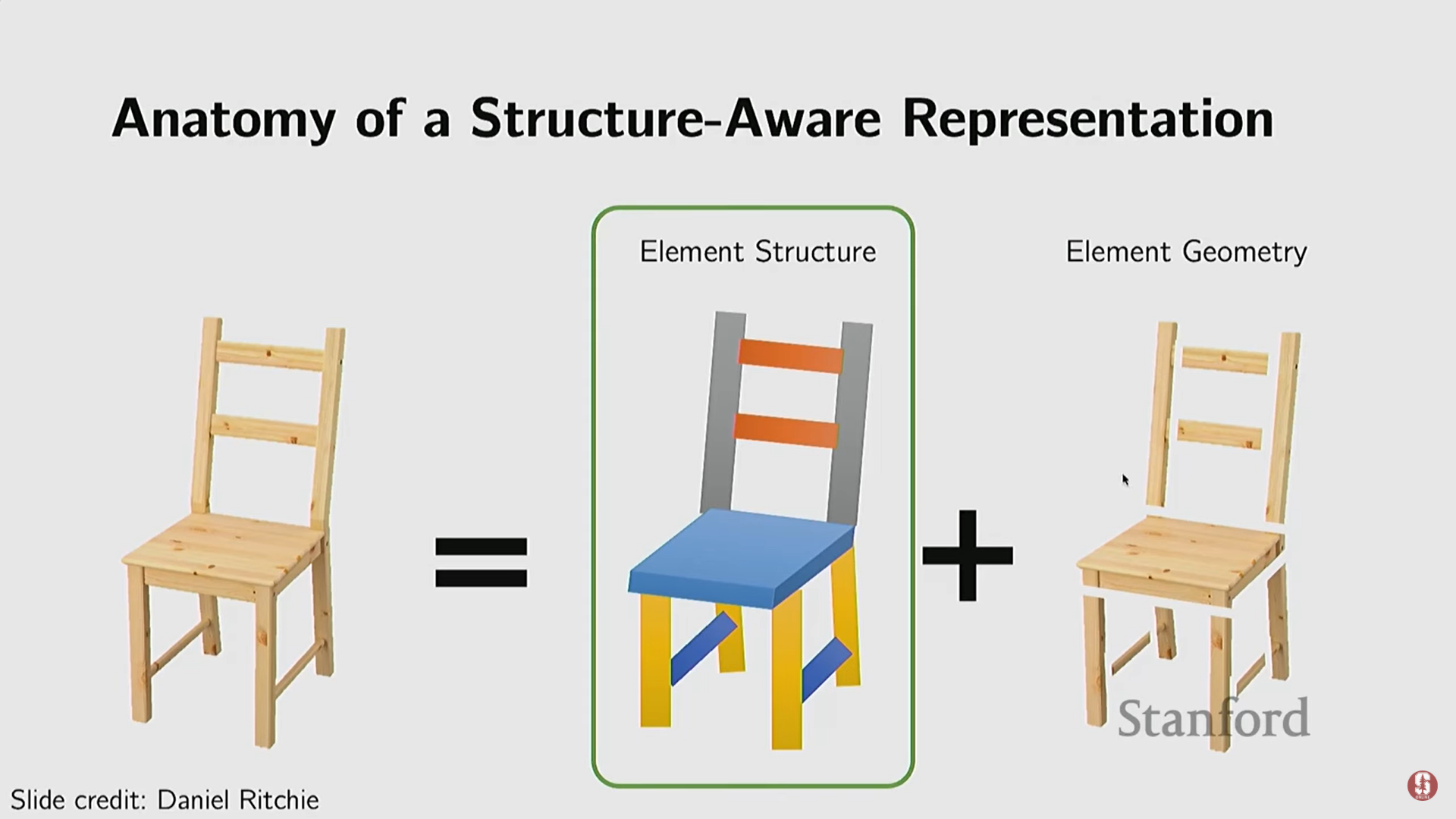
객체의 미세한 기하학적 형태를 넘어, 객체의 규칙성(regularities), 대칭성(symmetries), 그리고 부분 간의 구조(structure)를 포착하는 방법.
부분 기반 표현 (Part Set): 단순 기하학적 원시(primitives)를 사용하여 객체 부분을 표현하고 이를 합성한다.
관계 및 계층 모델링: 부품 간의 관계와 계층 구조(hierarchies)를 모델링한다 (예: 침대는 벽 옆에, 의자의 다리는 대칭이어야 함).
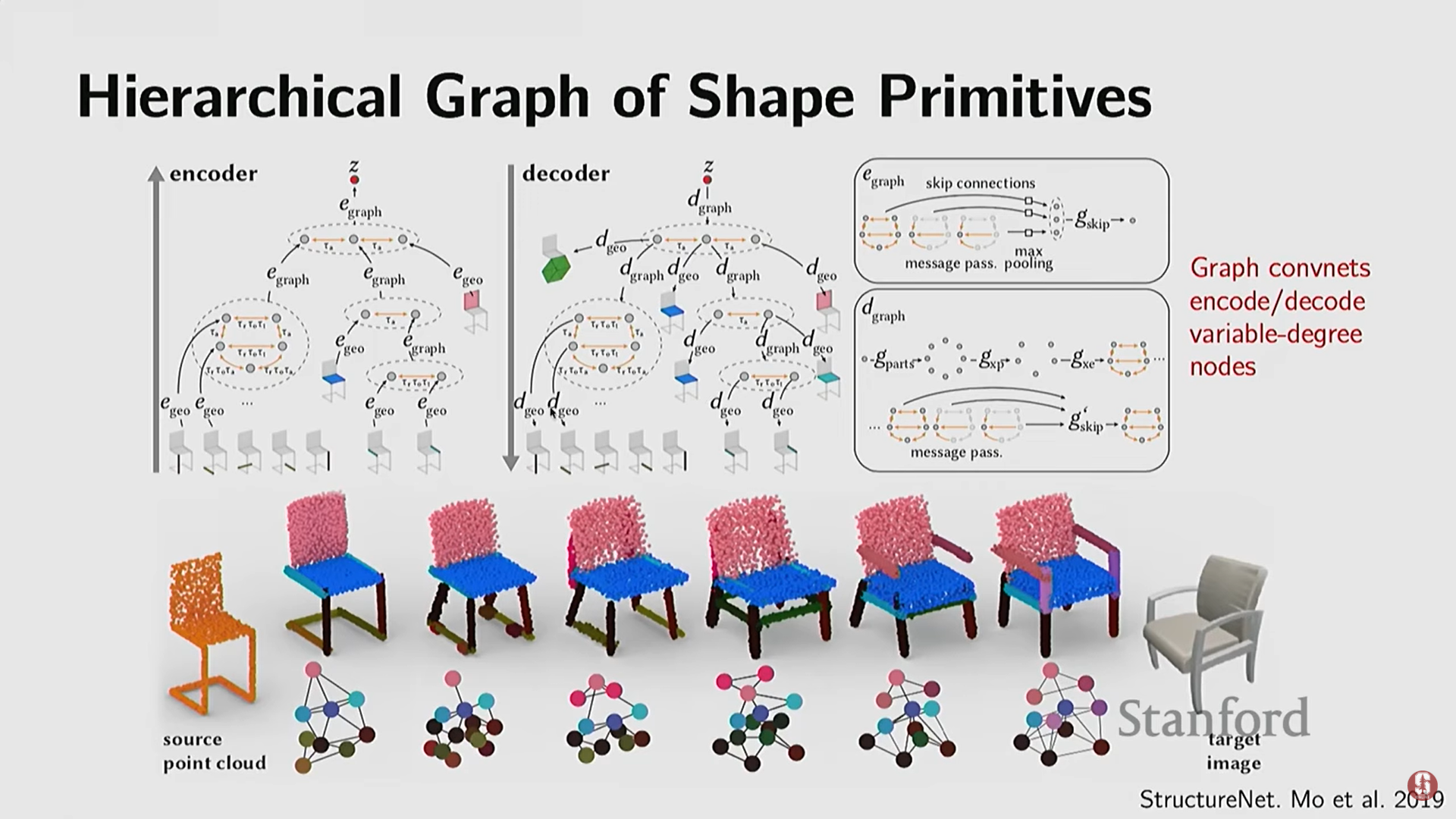
계층적 그래프 인코더/디코더: 딥러닝을 사용하여 이러한 계층적 제약 조건을 만족하는 3D 객체(예: 의자)를 생성하고 표현한다.
프로그램적 표현: 객체 구조의 반복성(repetitions)을 포착하기 위해 프로그램(programs) 형태를 사용하여 객체 모양과 부품 관계를 합성한다.
최신 동향: 대규모 언어 모델(LLMs, Large Language Models)이 의미론적 제약 조건을 잘 이해하므로, GPT와 같은 LLM을 사용하여 3D 객체의 구조를 정의하는 프로그램을 출력하고, 이후 암시적 함수를 사용하여 세부 기하학적 형태를 포착하는 연구가 진행 중이다.