[CV] CS236 11강 정리 [Energy Based Models]

김성윤(Jack)·2026년 1월 24일
CV

CV

목록 보기
29/32

1. 강의 개요 및 생성 모델의 설계 공간

오늘 강의에서는 에너지 기반 모델(Energy Based Models, EBM)에 대해 다룹니다. 이는 확산 모델(Diffusion Models)과 밀접하게 관련된 생성 모델의 한 종류입니다.

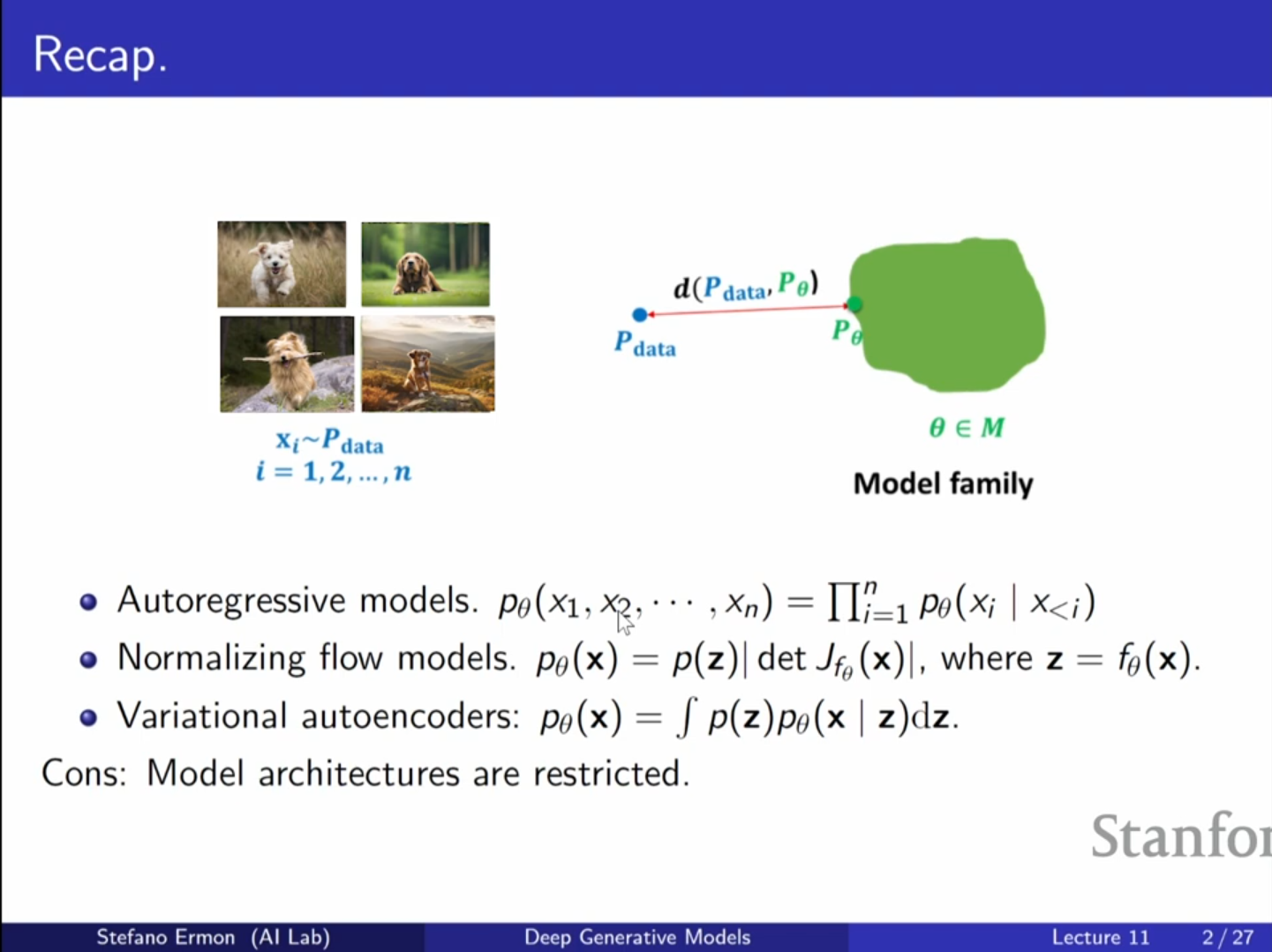
생성 모델을 구축할 때 우리는 알려지지 않은 데이터 분포에서 온 데이터를 가지고 모델 패밀리와 손실 함수(Loss function)를 정의해야 합니다. 지금까지 다룬 모델들은 다음과 같은 특징이 있습니다.

  • 자기회귀(Autoregressive) 모델, 노말라이징 플로우(Normalizing Flows): 우도(Likelihood)를 정확하게 계산할 수 있어 KL 발산(KL Divergence)을 최소화하는 방식(최대 우도 추정)이 자연스럽습니다.
  • VAE (Variational Autoencoders): 근사적으로 우도를 평가합니다.
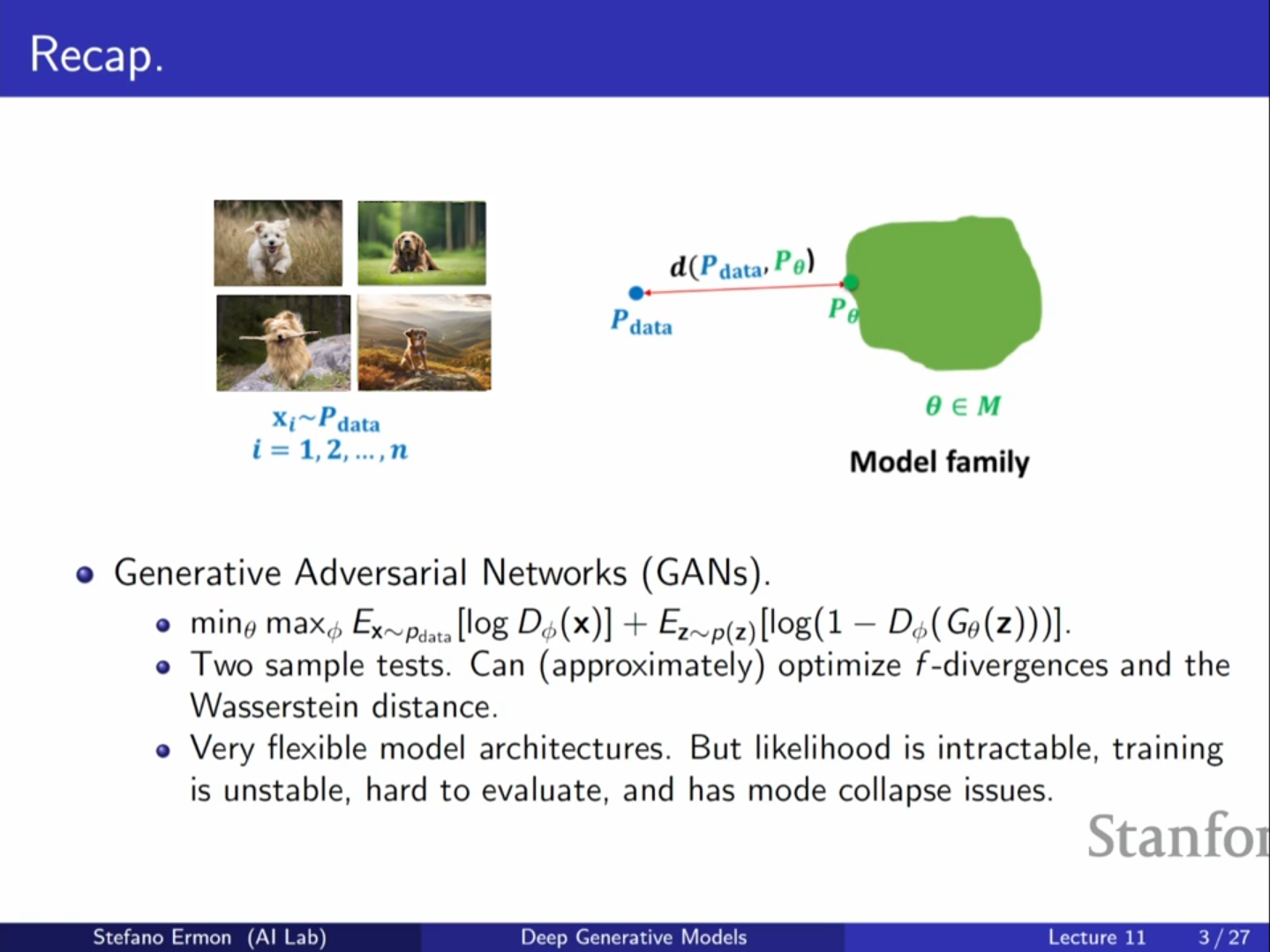
  • GAN (Generative Adversarial Networks): 확률 밀도를 명시적으로 정의하지 않고 샘플링 절차만 정의합니다. 이는 매우 유연하지만, 우도를 평가할 수 없어 Minimax 최적화라는 불안정한 학습 과정을 거쳐야 하며, 모드 붕괴(Mode collapse) 등의 문제가 발생합니다.

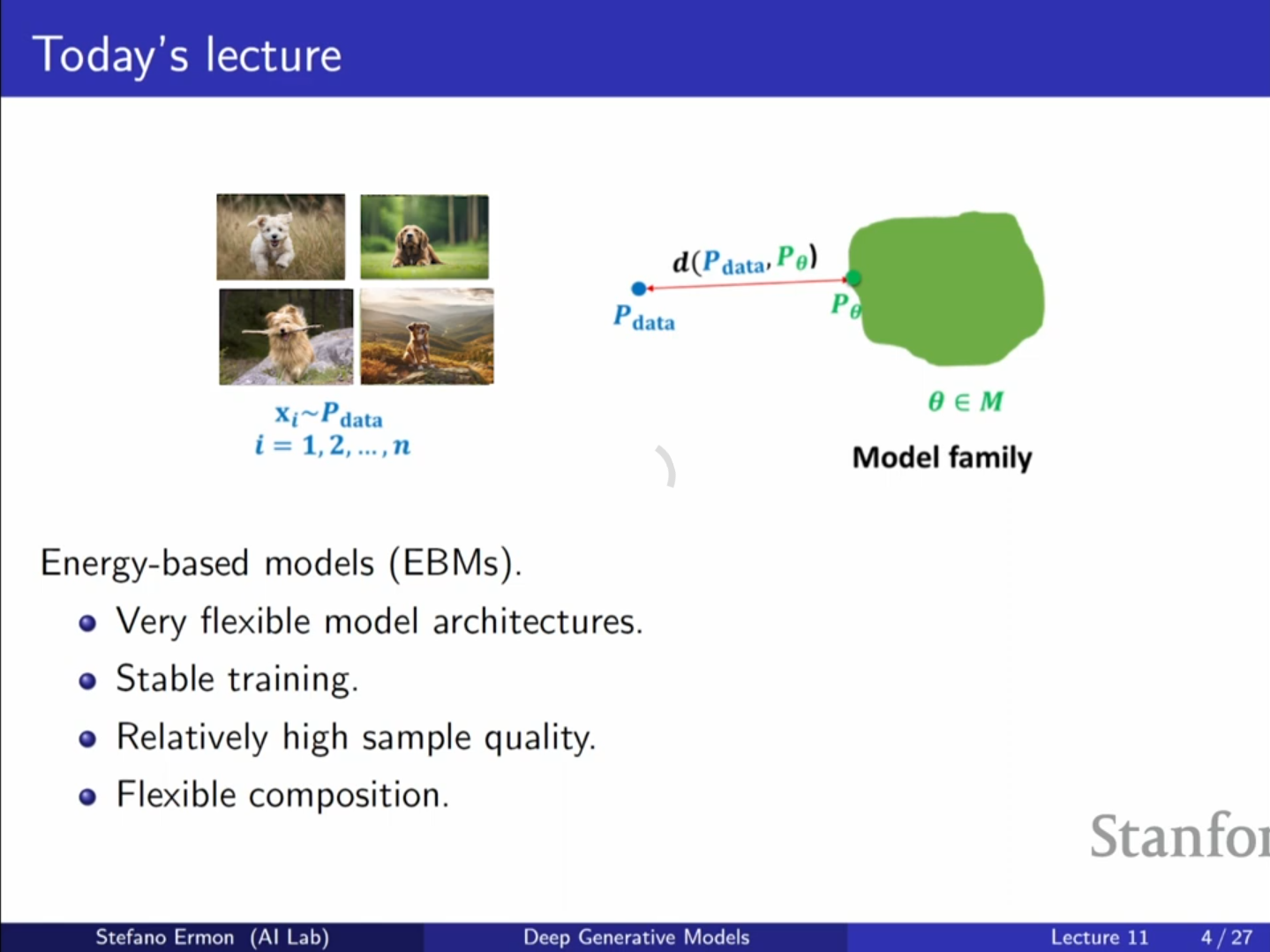
오늘 다룰 에너지 기반 모델은 신경망 구조에 대한 제약 없이 극도의 유연성을 제공하면서도, GAN과 달리 확률 모델의 특성을 활용하여 비교적 안정적인 학습 절차를 가집니다.

2. 확률 모델의 제약 조건과 EBM의 정의

확률 모델, 즉 확률 밀도 함수(PDF)나 확률 질량 함수(PMF)를 정의하기 위해서는 두 가지 제약 조건을 만족해야 합니다.

  1. 비음수성(Non-negativity): 모든 입력 xx에 대해 함수 값이 0보다 크거나 같아야 합니다. 이는 임의의 신경망 출력에 제곱을 하거나 지수(exponential)를 취함으로써 쉽게 달성할 수 있습니다.
  2. 정규화(Normalization): 가능한 모든 입력에 대한 확률의 합(또는 적분)이 1이어야 합니다.

2.1. 정규화의 어려움과 '케이크' 비유

정규화 제약은 만족시키기 매우 어렵습니다. 이를 '케이크'에 비유할 수 있습니다. 케이크의 전체 크기(총 확률 1)는 고정되어 있으므로, 한 조각(데이터 포인트의 확률)을 키우면 필연적으로 다른 조각은 줄어들어야 합니다.
자기회귀 모델이나 플로우 모델은 구조적으로 이 합이 1이 되도록 설계된 특수한 아키텍처를 사용합니다.

하지만 임의의 유연한 신경망을 사용할 경우, 파라미터 θ\theta에 따라 전체 적분 값(총 부피)이 변하게 됩니다.

2.2. 에너지 기반 모델의 해결책

EBM은 정규화되지 않은 함수를 허용하고, 이를 전체 적분 값으로 나누어 확률을 정의하는 방식을 취합니다.

Pθ(x)=exp⁡(fθ(x))Z(θ)P_\theta(x) = \frac{\exp(f_\theta(x))}{Z(\theta)}

여기서:

  • exp⁡(fθ(x))\exp(f_\theta(x)): 정규화되지 않은 확률(Unnormalized probability)입니다. 지수 함수를 사용하여 비음수성을 보장합니다.
  • Z(θ)Z(\theta): 분배 함수(Partition Function) 또는 정규화 상수입니다. 이는 Z(θ)=∫exp⁡(fθ(x))dxZ(\theta) = \int \exp(f_\theta(x)) dx 로 정의되며, 가능한 모든 입력에 대한 비정규화 확률의 합입니다.

이 방식을 통해 우리는 fθf_\theta에 대해 어떠한 구조적 제약도 받지 않는 임의의 신경망을 사용할 수 있습니다.

3. 지수족(Exponential Family)과 물리학적 배경


왜 fθ(x)f_\theta(x)를 그대로 쓰지 않고 지수 함수 exp⁡(fθ(x))\exp(f_\theta(x))를 사용할까요?

  1. 확률 변화의 폭: 지수 함수는 신경망 출력의 작은 변화로도 확률 값의 큰 차이를 만들어낼 수 있어, 잘 형성된 이미지와 노이즈 간의 확률 차이를 모델링하기 좋습니다.
  2. 통계학적 보편성: 가우시안, 포아송, 베르누이 등 많은 일반적인 분포들이 지수족(Exponential Family)에 속하며, 이들은 최대 엔트로피(Maximum Entropy) 가정 하에서 자연스럽게 도출됩니다.
  3. 물리학적 영감: 통계 물리학의 볼츠만 분포(Boltzmann distribution)에서 영감을 받았습니다. 여기서 −f(x)-f(x)는 에너지(Energy)로 해석됩니다. 에너지가 낮은 상태일수록 확률(exp⁡(−Energy)\exp(-Energy))이 높다는 개념을 따릅니다.

4. 정규화된 객체의 합성 vs EBM

기존 모델들(자기회귀, VAE 등)은 이미 정규화가 보장된 단순한 객체들을 결합하는 '트릭'으로 볼 수 있습니다.

  • 자기회귀 모델: 조건부 확률들의 곱으로 결합 확률을 정의하며, 각 조건부 확률이 정규화되어 있으므로 전체도 정규화됩니다.
  • 잠재 변수 모델(VAE): 정규화된 밀도들의 혼합(Mixture)으로 볼 수 있습니다.

반면, EBM은 이러한 구성적 제약을 깨고 분배 함수 Z(θ)Z(\theta)를 명시적으로 계산하거나 근사하는 방식을 택합니다.

5. EBM의 장단점 및 응용

장점: 유연성과 상대적 비교

  • 유연성: 아키텍처 선택에 제한이 없습니다.
  • 상대적 비교 용이성: 두 데이터 포인트 xx와 x′x' 중 어느 것이 더 그럴듯한지 비교할 때, Z(θ)Z(\theta)는 약분되어 사라지므로 계산할 필요가 없습니다. 즉, 비율 P(x)P(x′)\frac{P(x)}{P(x')}는 비정규화 확률만으로 계산 가능합니다.

단점: 계산 비용

  • 샘플링과 우도 평가의 어려움: 정확한 확률 P(x)P(x)를 알거나 새로운 샘플을 생성하려면 Z(θ)Z(\theta)를 알아야 하는데, 이는 고차원 공간에서 적분해야 하므로 계산이 불가능에 가깝습니다. 이를 차원의 저주(Curse of Dimensionality)라고 합니다.

응용 분야

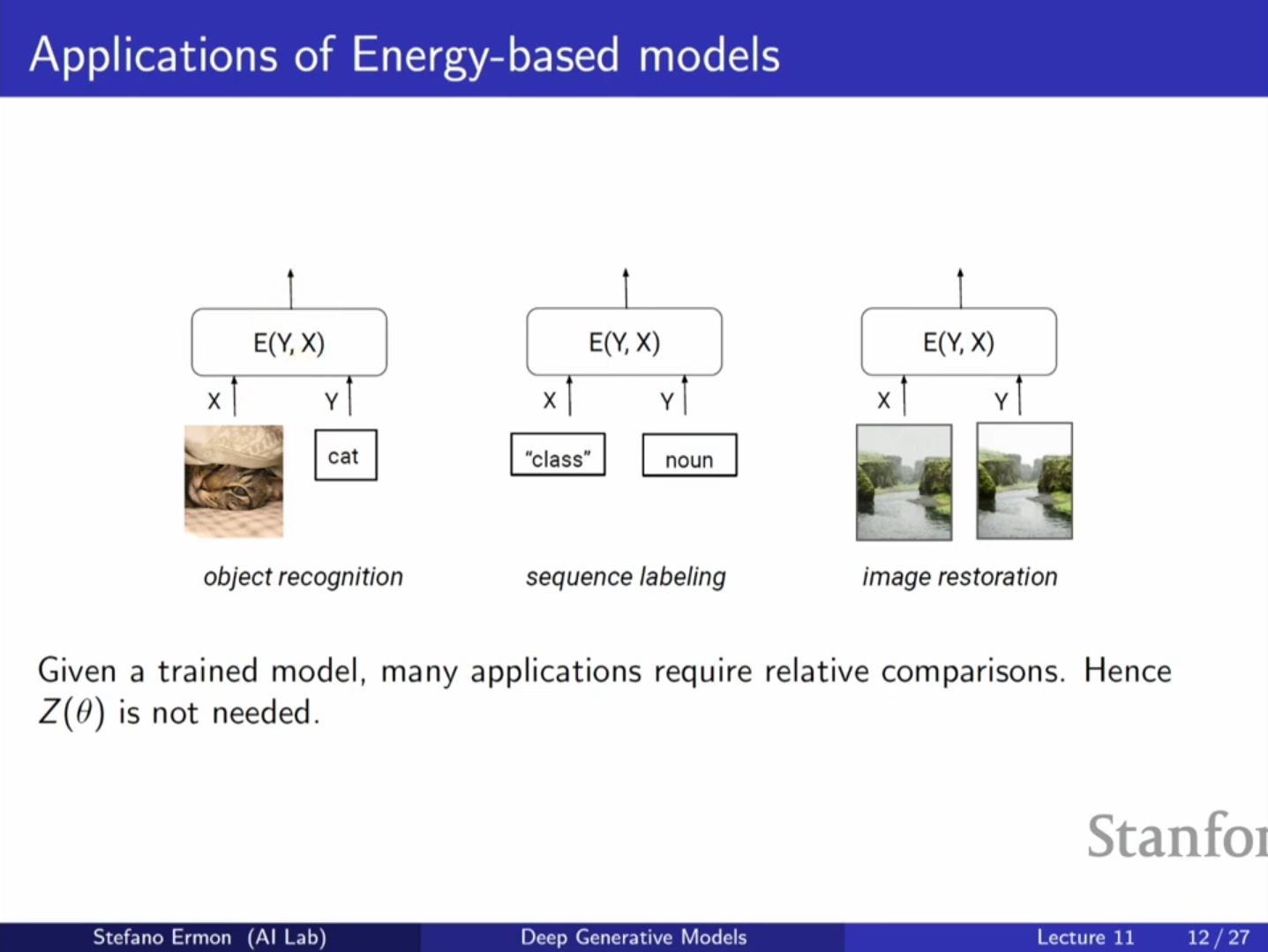
분배 함수 Z(θ)Z(\theta)를 몰라도 되는 작업들, 즉 상대적 비교만 필요한 작업에 유용합니다.

  • 이상치 탐지(Anomaly Detection)
  • Denoising: 손상된 이미지 XX에서 깨끗한 이미지 YY를 복원할 때, P(Y∣X)P(Y|X)를 최대화하는 YY를 찾는 과정에서 정규화 상수는 최적화 결과에 영향을 주지 않습니다.
  • 객체 인식 및 분류: 클래스 간의 상대적 점수만 비교하면 됩니다.

6. 전문가들의 곱 (Product of Experts)

EBM은 여러 모델을 결합하는 데에도 유용합니다. 여러 모델(전문가)의 확률을 곱하여 앙상블을 만들면, 이는 'AND' 연산처럼 동작합니다.

  • Product of Experts: 모든 모델이 동의해야 높은 확률을 가집니다. 하나라도 0을 출력하면 전체가 0이 됩니다. 이는 교집합(Intersection)의 개념과 유사합니다. 결과물은 다시 정규화가 필요하므로 EBM의 형태를 띱니다.
  • Mixture Models: 모델들의 합을 사용하며 'OR' 연산처럼 동작합니다. 하나만 높은 확률을 주어도 전체 확률이 존재합니다.

7. 제한된 볼츠만 머신 (Restricted Boltzmann Machine, RBM)

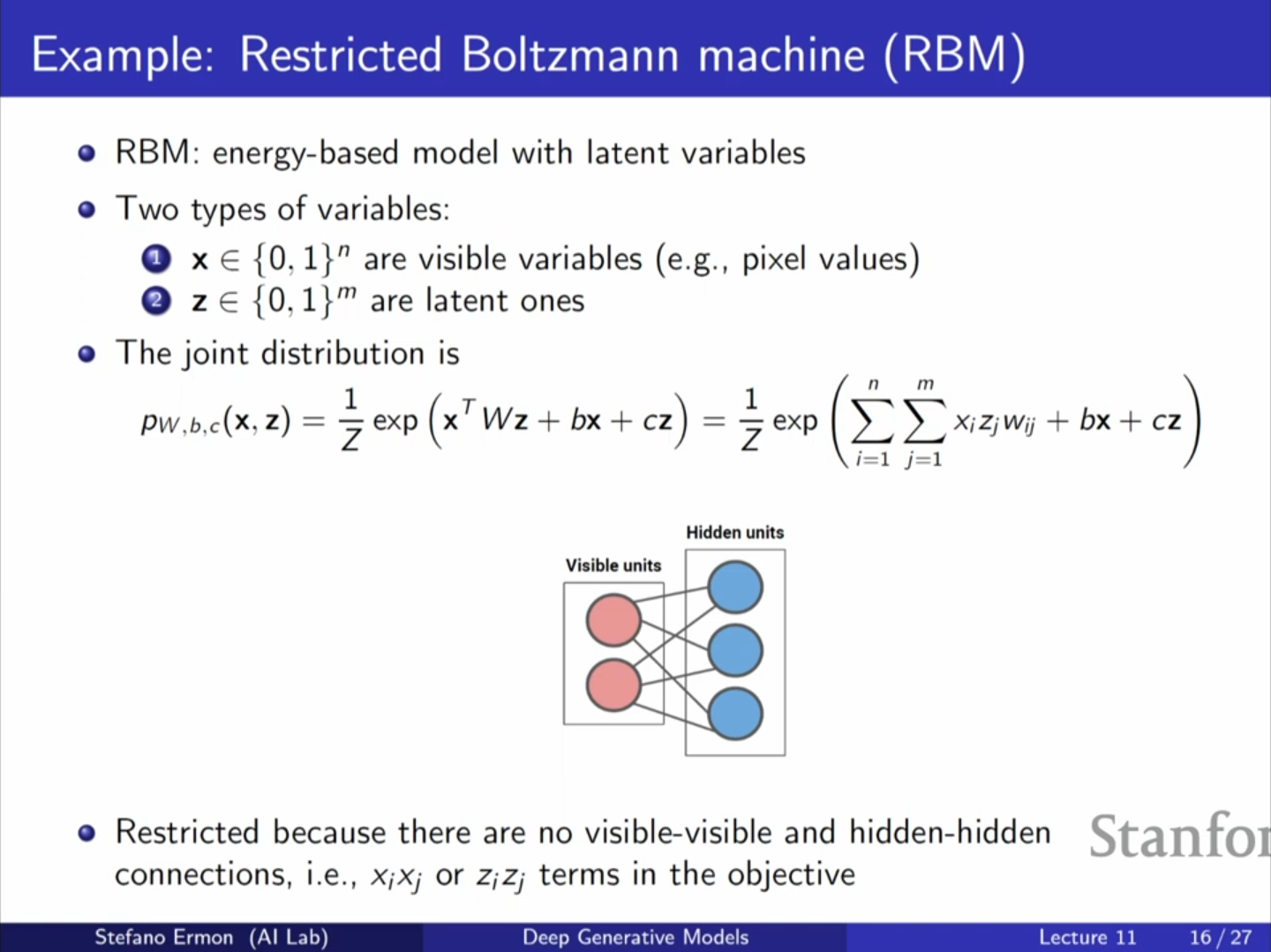
RBM은 가시적 유닛(Visible units) xx와 잠재 유닛(Hidden units) zz로 구성된 이산형 EBM입니다.

  • 에너지 함수: E(x,z)=−(xTWz+bTx+cTz)E(x, z) = - (x^T W z + b^T x + c^T z) 형태의 이차 형식을 가집니다.
  • 제약(Restricted): 같은 층의 유닛들(가시 유닛끼리 혹은 잠재 유닛끼리) 사이에는 연결이 없습니다.
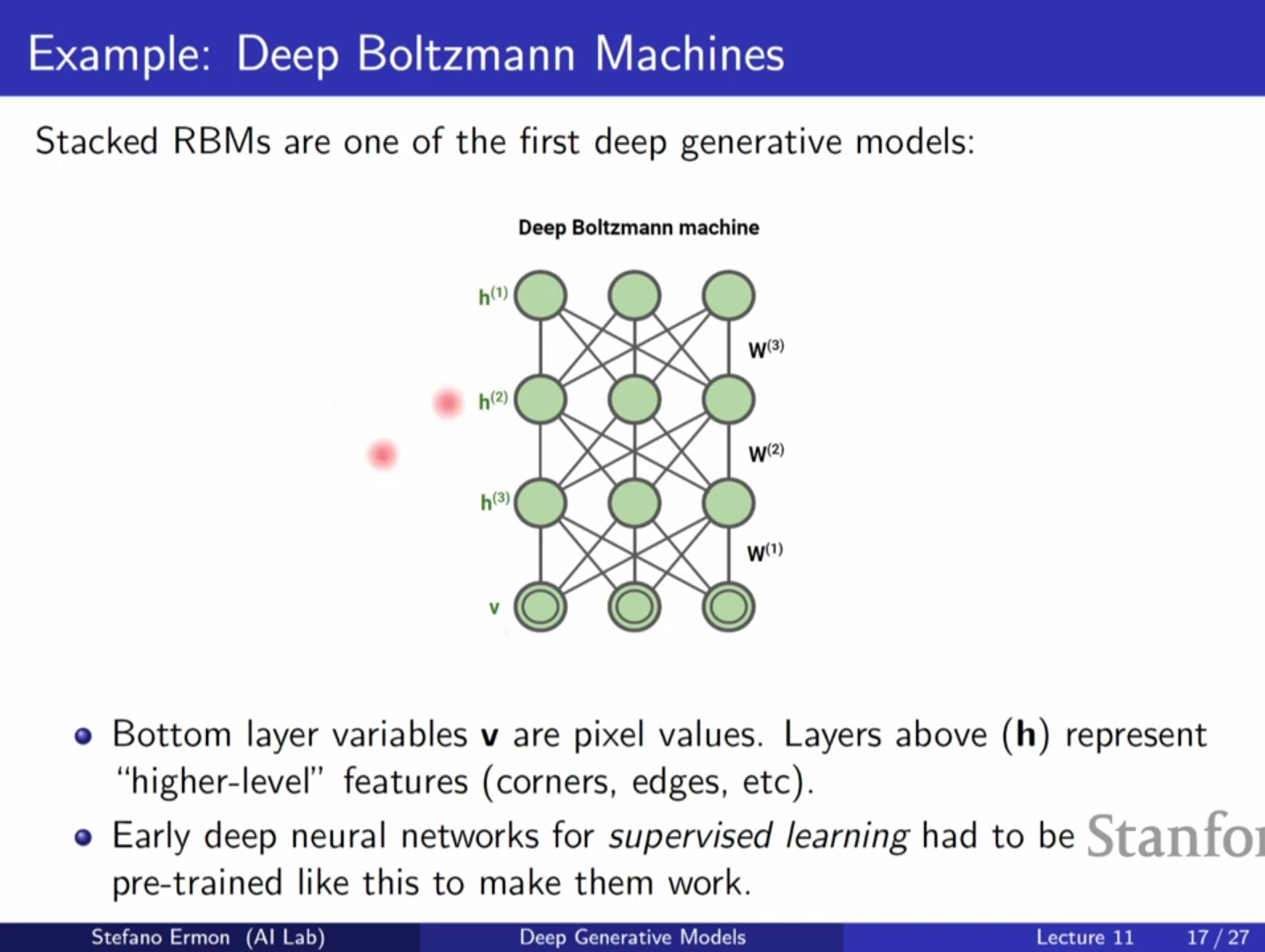
  • 의의: 딥러닝 초기(2009년경)에 심층 신경망을 학습시키기 위한 사전 학습(Pre-training) 용도로 사용되어 역사적으로 중요합니다.
  • 한계: 간단한 구조임에도 Z(θ)Z(\theta)를 계산하려면 2N+2M2^N + 2^M가지의 모든 경우의 수를 합해야 하므로 계산이 매우 비쌉니다.

8. EBM의 학습: 대조 발산 (Contrastive Divergence)

최대 우도 학습을 하려면 로그 우도의 기울기(Gradient)를 구해야 합니다.
∇θlog⁡Pθ(x)=∇θfθ(x)−∇θlog⁡Z(θ)\nabla_\theta \log P_\theta(x) = \nabla_\theta f_\theta(x) - \nabla_\theta \log Z(\theta)

이 수식의 의미는 다음과 같습니다:
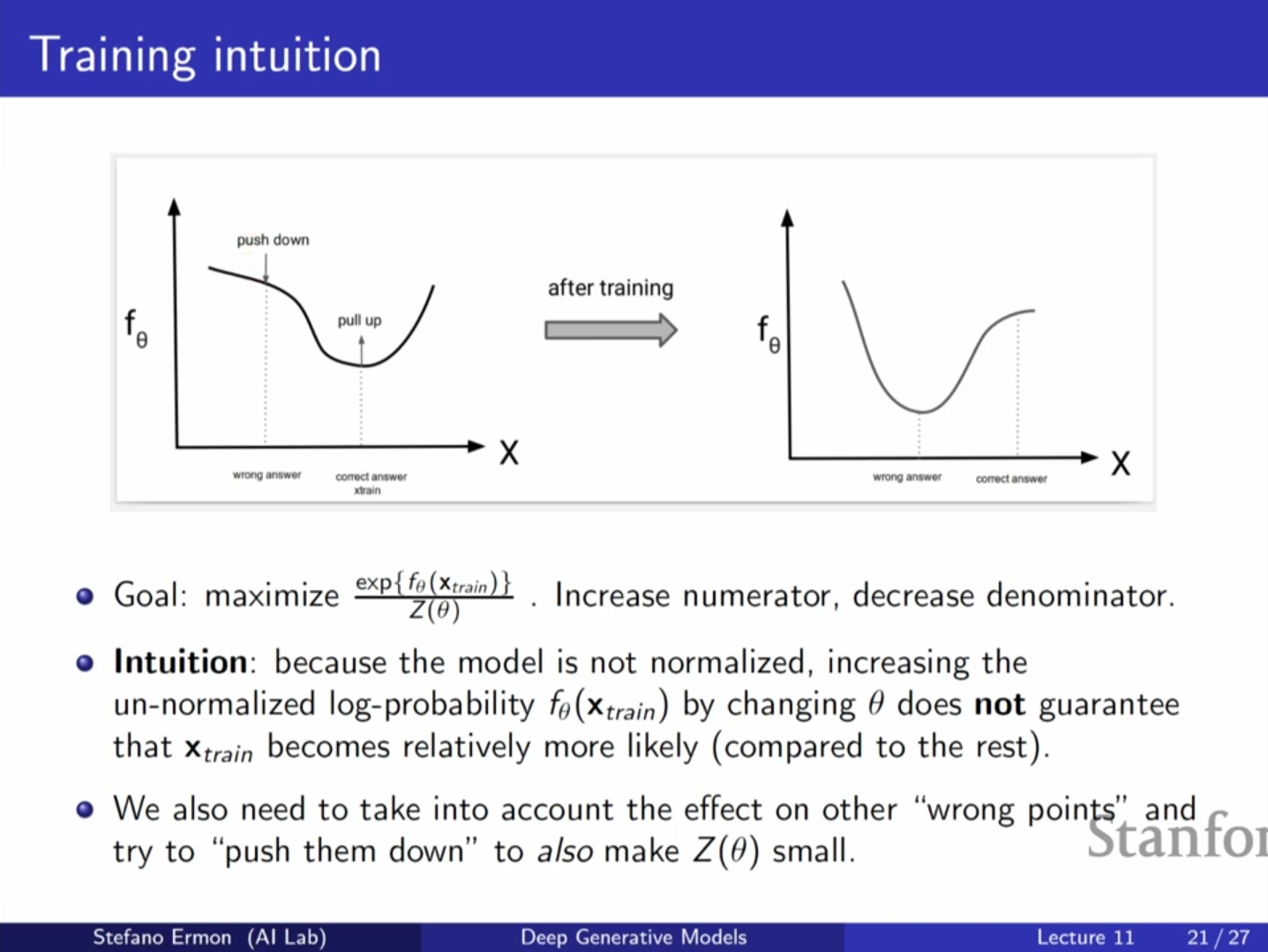
1. Positive Phase (∇θfθ(x)\nabla_\theta f_\theta(x)): 훈련 데이터 xx의 에너지를 낮춥니다(확률을 높임). 이는 계산하기 쉽습니다.
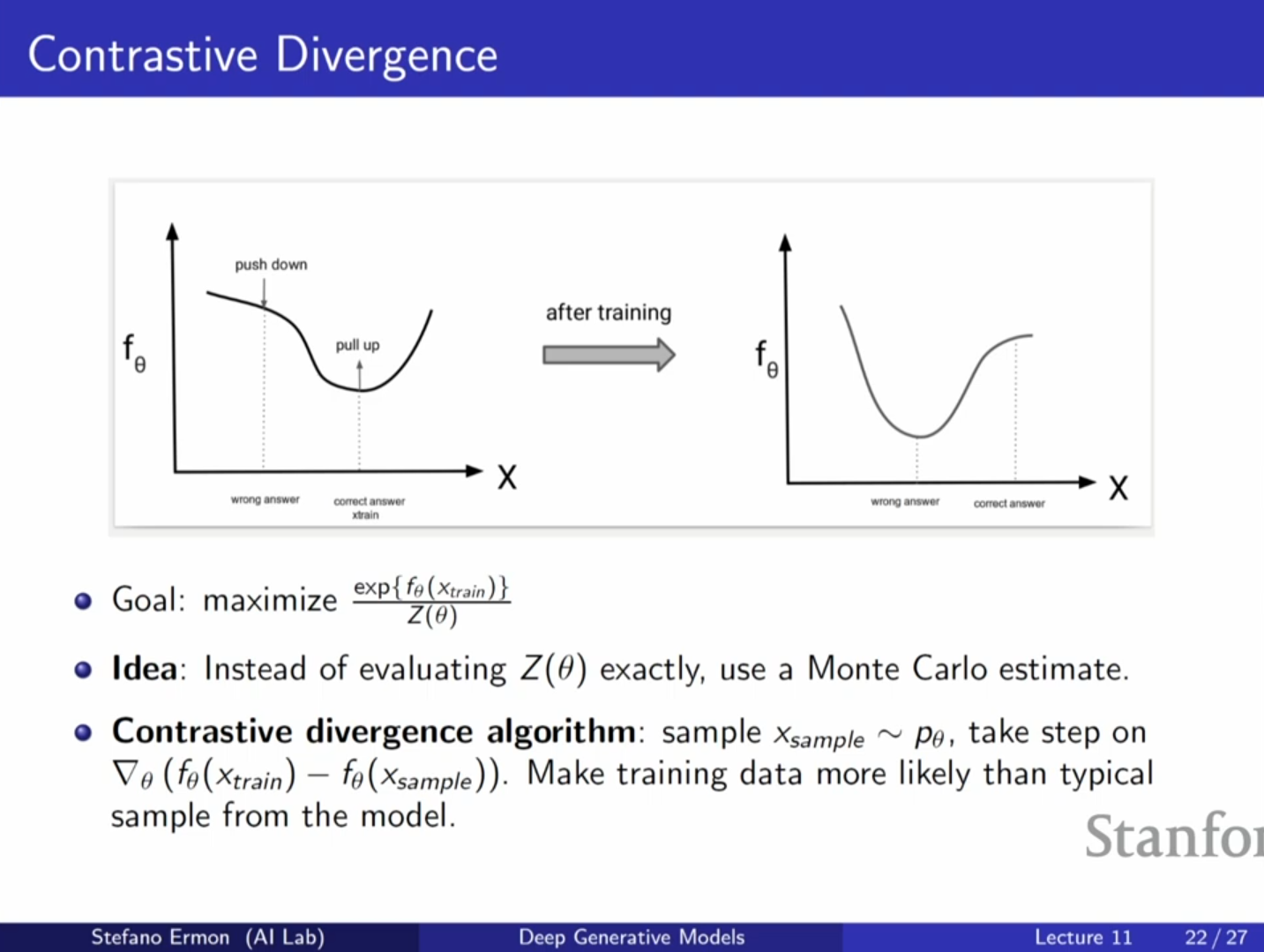
2. Negative Phase (∇θlog⁡Z(θ)\nabla_\theta \log Z(\theta)): 파라미터 변화가 전체 분배 함수(케이크의 전체 크기)를 얼마나 키우는지 보정해야 합니다. 수학적으로 이는 모델 분포에서 샘플링한 데이터 x′x'에 대한 기울기의 기댓값과 같습니다 (Ex′∼Pθ[∇θfθ(x′)]\mathbb{E}_{x' \sim P_\theta} [\nabla_\theta f_\theta(x')]).

즉, 학습의 목표는 훈련 데이터의 확률은 높이고, 모델이 생성한 샘플(Negative sample)의 확률은 낮추는 것입니다.

대조 발산(Contrastive Divergence) 알고리즘은 이 기댓값을 몬테카를로 방법으로 근사합니다. 즉, 모델에서 샘플 x′x'을 하나 뽑아서 그 샘플에 대한 기울기를 뺍니다.

∇θlog⁡Pθ(x)≈∇θfθ(xdata)−∇θfθ(xsample)\nabla_\theta \log P_\theta(x) \approx \nabla_\theta f_\theta(x_{data}) - \nabla_\theta f_\theta(x_{sample})

이 방식은 실제 기울기에 대한 불편 추정량(Unbiased estimator)을 제공합니다.

9. 샘플링 방법: MCMC (Markov Chain Monte Carlo)

EBM에서 샘플을 추출하는 것은 어렵지만, MCMC 방법을 사용하여 근사적으로 수행할 수 있습니다.

  1. 임의의 샘플 x0x_0에서 시작합니다.
  2. 노이즈를 추가하여 새로운 제안 x′x'을 만듭니다.
  3. 비교: 현재 샘플 xtx_t와 제안된 샘플 x′x'의 확률(에너지)을 비교합니다. ZZ를 몰라도 비율은 계산 가능합니다.
  4. 이동 규칙:
    • 확률이 높아지면(에너지가 낮아지면) 무조건 이동합니다.
    • 확률이 낮아지더라도, 확률적으로 이동을 허용합니다 (Metropolis-Hastings 알고리즘). 이는 지역 최적해(Local Optimum)에 갇히지 않고 전체 공간을 탐색하기 위함입니다.

이 과정을 충분히 반복하면 이론적으로 모델의 분포를 따르는 샘플을 얻을 수 있습니다.

10. QnA: 강의 중 주요 질문과 답변

Q1. Softmax도 EBM의 일종인가요?

  • A1: 네, 그렇습니다. Softmax는 신경망의 출력(Logits)을 확률로 변환하는 방식으로, 구조적으로 EBM과 같습니다. 다만 분류 문제에서는 클래스의 수(KK)가 적어서 분모(분배 함수)를 정확하게 계산할 수 있다는 점이 다릅니다. 오늘 다루는 EBM은 xx의 차원이 매우 커서 분모를 계산할 수 없는 경우에 초점을 맞춥니다.

Q2. VAE의 재구성 우도(Reconstruction likelihood)에서 Softmax를 쓰는데, VAE와 EBM은 어떻게 다른가요?

  • A2: EBM은 더 일반적인 용어입니다. VAE나 자기회귀 모델도 Z=1Z=1이 되도록 강제한 특수한 EBM으로 볼 수 있습니다. 하지만 좁은 의미의 EBM은 ZZ가 1이 아니며 이를 분석적으로 알 수 없는 경우를 지칭합니다.

Q3. Product of Experts에서 샘플링은 어떻게 하나요?

  • A3: 어렵습니다. 추론 시 많은 계산 비용을 지불해야 합니다. 이것이 EBM의 대가입니다. 하지만 가능은 하며 확산 모델(Diffusion Model) 등이 이와 관련되어 있습니다.

11. 핵심 내용 요약

  1. 유연성과 정규화의 트레이드오프: 에너지 기반 모델(EBM)은 정규화 제약(적분값이 1)을 포기하는 대신, 모델 아키텍처 설계에 있어 극도의 유연성을 확보합니다. 정규화는 분배 함수 Z(θ)Z(\theta)를 통해 사후적으로 처리됩니다.
  2. 분배 함수의 난제: Z(θ)Z(\theta)를 계산하는 것은 고차원 적분을 필요로 하여 매우 어렵습니다(차원의 저주). 따라서 EBM은 정확한 우도 계산이나 샘플링이 어렵지만, 상대적 비교가 필요한 작업에는 매우 효율적입니다.
  3. 학습 및 샘플링 전략: EBM은 대조 발산(Contrastive Divergence)을 통해 데이터의 에너지는 낮추고 모델 샘플의 에너지는 높이는 방식으로 학습합니다. 이때 샘플링을 위해 MCMC 같은 반복적인 근사 방법을 사용합니다.
profile
김성윤(Jack)
AI 공부합니다
이전 포스트

[CV] CS236 10강 정리 [GANs]

다음 포스트

[CV] CS236 12강 정리 [Energy Based Models]

0개의 댓글