[CV] CS236 12강 정리 [Energy Based Models]

김성윤(Jack)·2026년 1월 24일

CV

목록 보기

30/32

1. 에너지 기반 모델(EBM)과 샘플링의 한계

EBM의 복습 및 난제

에너지 기반 모델은 정규화되지 않은 확률 분포(unnormalized probability distribution)를 정의하는 매우 유연한 방법입니다.
모델의 확률 분포는 다음과 같이 정의됩니다.
$P_\theta(x) = \frac{\exp(-f_\theta(x))}{Z(\theta)}$
여기서 $f_\theta(x)$ 는 에너지 함수(신경망 등)이며, $Z(\theta)$ 는 파티션 함수(정규화 상수)입니다.
핵심 문제: $Z(\theta)$ 를 계산하는 것은 가능한 모든 $x$ 에 대해 적분하거나 합을 구해야 하므로 일반적으로 불가능(intractable)합니다. 따라서 데이터 포인트의 우도(likelihood)를 직접 평가하는 것이 어렵습니다.

대조 발산(Contrastive Divergence)의 한계

지난 강의에서 다룬 대조 발산(CD)은 모델로부터 샘플을 생성하여 로그 파티션 함수의 기울기를 근사하는 방법입니다.
하지만 훈련 과정의 내부 루프(inner loop)에서 샘플링을 반복해야 하므로 계산 비용이 매우 높다는 단점이 있습니다. 특히 MCMC(Markov Chain Monte Carlo)를 사용하여 샘플링할 경우 많은 스텝이 필요하여 학습 속도가 느려집니다.

2. 랑주뱅 다이내믹스 (Langevin Dynamics)

모델로부터 더 효율적으로 샘플링하기 위한 방법으로 랑주뱅 다이내믹스가 소개되었습니다.

작동 원리

개념: 기존의 무작위 섭동(random perturbation) 대신, 로그 우도의 기울기(gradient) 정보를 활용하여 확률이 높은 영역으로 샘플을 이동시키는 방법입니다.
업데이트 규칙:
$x_{t+1} = x_t + \epsilon \nabla_x \log p_\theta(x_t)|_{x=x^t}+ \sqrt{2\epsilon} \cdot z_t$
여기서 $z_t$ 는 가우시안 노이즈입니다.
기울기를 따라 이동(Gradient Ascent)하여 확률을 높이되, 노이즈를 추가하여 국소 최적해(local optima)에 갇히지 않고 탐색(exploration)을 수행합니다.

특징 및 한계

장점: 기울기 정보를 사용하므로 단순한 MCMC보다 수렴 속도가 빠르고 더 나은 제안(proposal)을 할 수 있습니다.
심화 내용: $\nabla_x \log p_\theta(x)$ 를 계산할 때, 파티션 함수 $Z(\theta)$ 는 $x$ 에 의존하지 않으므로 미분 시 사라집니다. 따라서 정규화 상수를 몰라도 에너지 함수 $f_\theta(x)$ 의 기울기만으로 샘플링이 가능합니다.
한계: 추론(Inference) 시에는 유용하지만, 학습 과정에서 매번 수행하기에는 여전히 비용이 많이 듭니다.

3. 스코어 매칭 (Score Matching)

샘플링 없이 EBM을 학습시키기 위한 첫 번째 대안으로 스코어 매칭이 제시됩니다.

스코어 함수 (Score Function)

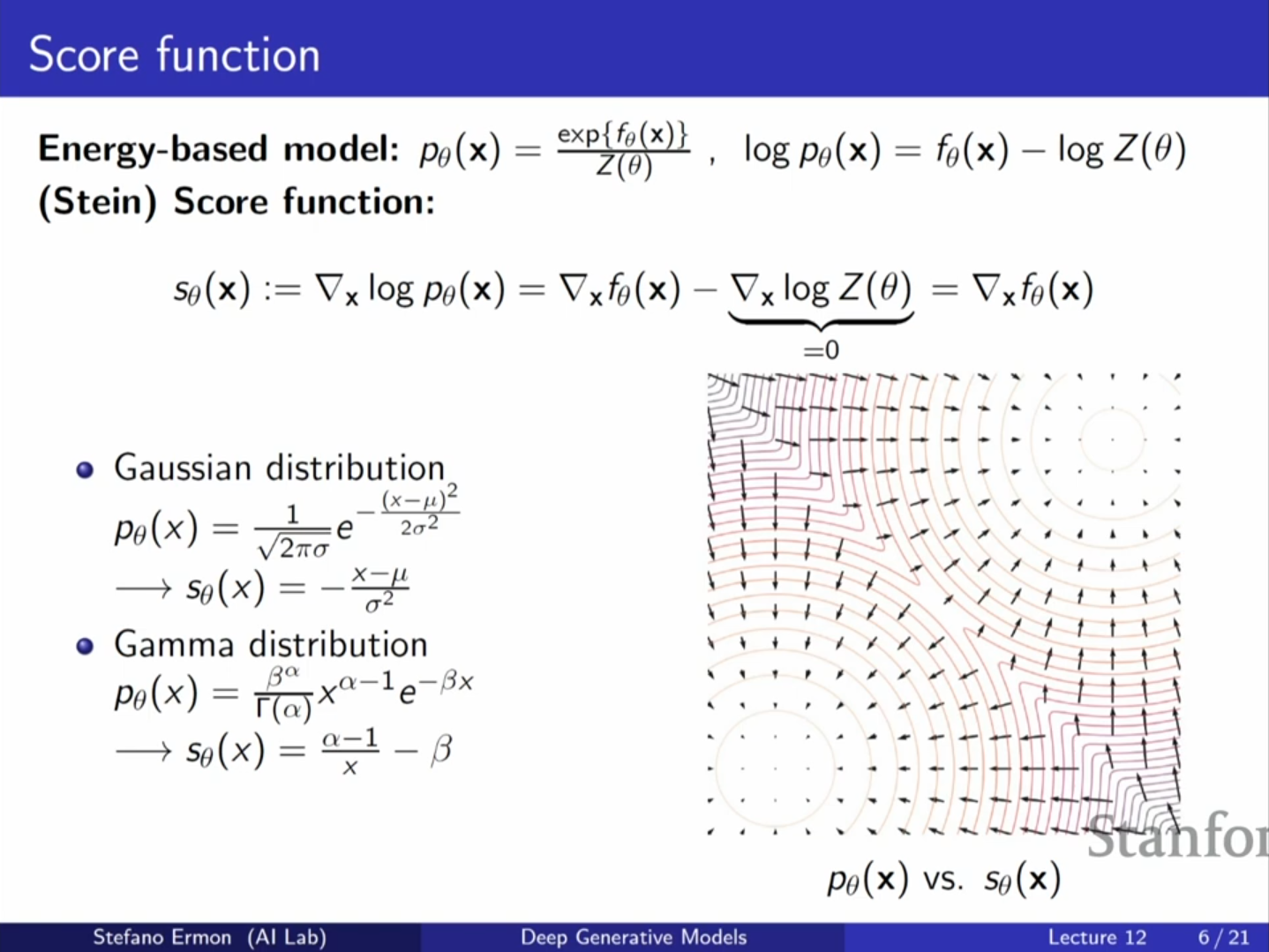
정의: 스코어 함수 $s_\theta(x)$ 는 로그 우도의 데이터 $x$ 에 대한 기울기로 정의됩니다.
$s_\theta(x) = \nabla_x \log p_\theta(x)$
핵심 성질: 앞서 언급했듯, 로그 우도를 미분하면 파티션 함수 항( $\log Z(\theta)$ )은 $x$ 와 무관하므로 사라집니다. 즉, 스코어 함수는 $Z(\theta)$ 에 의존하지 않습니다.
물리학적 비유: 에너지 함수 $f_\theta$ 를 전위(electric potential)로 본다면, 스코어 함수는 전기장(electric field, 벡터장)에 해당합니다.

피셔 발산 (Fisher Divergence)

두 확률 분포 $p$ 와 $q$ 를 비교하기 위해, 그들의 스코어(기울기 벡터장)가 얼마나 다른지를 측정합니다. 이를 피셔 발산이라고 합니다.
목적함수: 데이터 분포 $p_{data}$ 와 모델 분포 $p_\theta$ 사이의 차이를 최소화합니다.
$J(\theta) = \frac{1}{2} \mathbb{E}_{x \sim p_{data}} [ || \nabla_x \log p_{data}(x) - \nabla_x \log p_\theta(x) ||_2^2 ]$
난점: 이 식은 실제 데이터 분포의 스코어 $\nabla_x \log p_{data}(x)$ 를 알아야 계산할 수 있는데, 우리는 이를 알지 못합니다.

부분 적분을 통한 해결 (Integration by Parts)

심화 내용 (핵심 트릭): 부분 적분(다변수의 경우 발산 정리 등)을 사용하여 목적함수를 변형하면, 데이터의 스코어 항을 제거할 수 있습니다.
변형된 손실 함수는 다음과 같습니다(1차원 예시):
$J(\theta) \approx \mathbb{E}_{x \sim p_{data}} \left[ \frac{1}{2} \left( \frac{\partial^2 \log p_\theta(x)}{\partial x^2} \right)^2 + \frac{\partial^2 \log p_\theta(x)}{\partial x^2} \right]$
이 식은 모델의 스코어 제곱항과, 로그 우도의 2계 도함수(Hessian의 Trace) 항으로 구성됩니다.
의미:
1. 첫 번째 항: 데이터 포인트에서 기울기를 0에 가깝게 만듭니다 (데이터가 극점이 되도록 함).
2. 두 번째 항(Trace of Hessian): 데이터 포인트가 극소값이 아닌 극대값(local maxima)이 되도록 곡률을 조정합니다.

한계점

고차원 데이터에서 헤시안(Hessian) 행렬의 트레이스(Trace)를 계산하는 것은 계산 비용이 매우 높습니다. 이를 해결하기 위해 Sliced Score Matching 등의 근사법이 존재합니다.

4. 잡음 대조 추정 (Noise Contrastive Estimation, NCE)

샘플링을 피하는 두 번째 방법으로, 생성 문제를 분류 문제(Classification)로 치환하는 방법입니다.

기본 아이디어

데이터 분포 $P_{data}$ 와 우리가 선택한 잡음 분포(Noise Distribution) $P_n$ 을 구별하는 판별기(Discriminator)를 학습시킵니다.
판별기의 최적 형태: 데이터와 잡음을 구분하는 최적의 판별기 $D_{\theta*}(x)$ 는 밀도 비율(density ratio)로 나타납니다.
$D_{\theta*}(x) = \frac{P_{data}(x)}{P_{data}(x) + P_n(x)}$

EBM 학습에의 적용

판별기를 임의의 신경망으로 두는 대신, 우리의 EBM 모델 $P_\theta$ 를 사용하여 정의합니다.
$D_\theta(x) = \frac{P_\theta(x)}{P_\theta(x) + P_n(x)} = \frac{\frac{1}{Z} e^{-f_\theta(x)}}{\frac{1}{Z} e^{-f_\theta(x)} + P_n(x)}$
Z의 처리: 여기서 $Z$ 를 계산 불가능한 상수로 두지 않고, 학습 가능한 파라미터 $Z$ 로 취급하여 $\theta$ 와 함께 최적화합니다.
학습 과정: 실제 데이터는 'True', 잡음 샘플은 'False'로 레이블링하여 이진 교차 엔트로피(Binary Cross Entropy) 손실 함수로 학습합니다.

특징 및 GAN과의 차이

장점: 모델로부터 샘플링할 필요가 없습니다. 잡음 분포 $P_n$ 에서만 샘플링하면 되며, 이는 효율적입니다.
심화 내용: 데이터가 무한하고 최적화가 완벽하다면, 학습된 $P_\theta$ 는 $P_{data}$ 로 수렴하고, 학습 파라미터 $Z$ 는 실제 파티션 함수 값으로 수렴함이 증명되어 있습니다.
GAN과의 비교: GAN은 생성자(Generator)를 학습시켜 판별기를 속이려 하지만, NCE는 잡음 분포가 고정(fixed)되어 있고 판별기 내부의 밀도 모델을 학습시키는 데 집중합니다.

5. 플로우 대조 추정 (Flow Contrastive Estimation)

배경: NCE의 성능은 잡음 분포 $P_n$ 이 얼마나 데이터와 유사한지에 따라 달라집니다. 잡음이 너무 쉬우면 학습이 잘 되지 않습니다.
개선안: 잡음 분포 $P_n$ 을 고정하지 않고, Flow 모델 등을 사용하여 학습 가능한 분포로 설정합니다.
적대적 학습: Flow 모델은 판별기를 최대한 헷갈리게 하도록(데이터와 비슷하게) 학습하고, EBM 기반의 판별기는 이를 구분하도록 학습하는 Minimax 게임 형태를 취합니다.
이는 GAN과 유사한 구조를 가지며, 결과적으로 더 좋은 품질의 샘플을 얻을 수 있습니다.

6. Q&A (강의 중 질의응답)

Q1: 랑주뱅 다이내믹스에서 기울기를 더하는 것만으로 충분하지 않나요? 왜 노이즈를 추가하나요?
A1: 기울기만 따르면 우도(likelihood)를 최대화하는 방향으로만 이동하게 되어 국소 최적해(local maxima)에 갇힐 수 있습니다. 노이즈를 추가함으로써 공간을 탐색(explore)할 수 있게 되고, 이론적으로 충분한 시간이 지나면 진정한 모델 분포에서 샘플링한 것과 같아지게 됩니다.

Q2: 스코어 매칭에서 2번 식(데이터 스코어 항 제거 식)이 성립하는 이유가 무엇인가요?
A2: 부분 적분(Integration by Parts)을 사용했기 때문입니다. 데이터 밀도 함수가 $\pm \infty$ 에서 0으로 수렴한다는 가정 하에 경계 조건이 사라지면서, 데이터 분포의 스코어 항을 모델 스코어의 도함수 항으로 변환할 수 있습니다.

Q3: NCE에서 $Z$ 를 그냥 학습 가능한 파라미터로 두면, 이것이 실제 파티션 함수가 아닐 수도 있지 않나요?
A3: 맞습니다. 학습 중간에는 실제 파티션 함수와 다를 수 있어 유효한 확률 분포가 아닐 수 있습니다. 하지만 데이터가 충분하고 최적화가 잘 이루어진 극한(limit) 상황에서는, 최적의 $Z$ 값이 실제 파티션 함수 값으로 수렴하게 됩니다.

Q4: 헤시안(Hessian)의 트레이스(Trace)를 구하는 것은 어렵지 않나요?
A4: 맞습니다. 고차원에서는 매우 비용이 많이 듭니다. 그래서 실제로는 Hutchinson Trace Estimator나 Sliced Score Matching 같은 근사법을 사용하여 계산 효율성을 높입니다.

7. 핵심 내용

랑주뱅 다이내믹스(Langevin Dynamics)는 로그 우도의 기울기를 활용하여 EBM에서 샘플링하는 방법이지만, 학습 시 반복 사용하기에는 여전히 계산 비용이 높습니다.
스코어 매칭(Score Matching)은 샘플링 없이 데이터와 모델의 기울기 벡터장(Score)을 일치시키는 학습법으로, 부분 적분 트릭을 통해 파티션 함수 $Z(\theta)$ 없이 학습이 가능합니다. 단, 고차원에서는 2계 도함수 계산이 부담될 수 있습니다.
잡음 대조 추정(NCE)은 생성 모델 학습을 '데이터 vs 잡음'의 이진 분류 문제로 변환하여 $Z$ 를 학습 가능한 파라미터로 취급합니다. 이를 통해 우도 계산이나 모델 샘플링 없이 EBM을 효율적으로 학습할 수 있습니다.

김성윤(Jack)

AI 공부합니다

이전 포스트

[CV] CS236 11강 정리 [Energy Based Models]

다음 포스트