1. 자기회귀 모델(Auto-regressive Models) 복습 및 한계

• 자기회귀 모델의 특징: 연쇄 법칙(Chain Rule)을 사용하여 결합 확률 분포를 조건부 확률의 곱으로 표현합니다. RNN, CNN, Transformer 등의 신경망을 통해 이러한 조건부 확률을 근사합니다.
• 장점: 우도(Likelihood)에 직접 접근할 수 있어 데이터의 확률을 평가하기 쉽고, 이를 통해 최대 우도 추정(Maximum Likelihood Estimation, MLE) 및 이상치 탐지(Anomaly Detection)가 용이합니다.
• 단점:
  • 변수 간의 순서를 정해야 하며, 이는 때때로 까다로운 문제입니다.
  • 생성 속도가 느림: Transformer와 같은 병렬 구조를 사용하더라도, 샘플 생성 시에는 한 번에 하나의 변수씩 생성해야 하므로 비효율적입니다.
  • 무감독 특징 추출(Unsupervised Feature Extraction): 데이터로부터 유용한 특징을 추출하는 방법이 직관적이지 않습니다.

---

2. 잠재 변수 모델(Latent Variable Models, LVM)의 등장 배경

• 복잡한 데이터의 가변성: 사람의 얼굴 이미지 데이터셋을 모델링할 때, 나이, 포즈, 머리카락 색상, 눈 색상 등 수많은 가변 요소(Variability)가 존재합니다.
• 잠재 변수의 정의: 이러한 요소들은 데이터셋에 직접 주석(Annotation)이 달려 있지 않지만, 데이터의 픽셀 값에 영향을 미치는 숨겨진 구조입니다. 이를 잠재 변수(Latent Variables) 또는 숨겨진 변수(Hidden Variables) $z$라고 정의합니다.
• 잠재 변수 모델의 이점:
  • 모델의 유연성이 증대됩니다.
  • 관찰된 픽셀 값($x$)으로부터 잠재 변수($z$)를 역으로 추론함으로써 유용한 특징을 추출할 수 있습니다(표현 학습).
  • $P(x)$를 직접 모델링하는 것보다 $z$가 주어졌을 때의 조건부 확률 $P(x|z)$를 모델링하는 것이 훨씬 간단합니다.

---

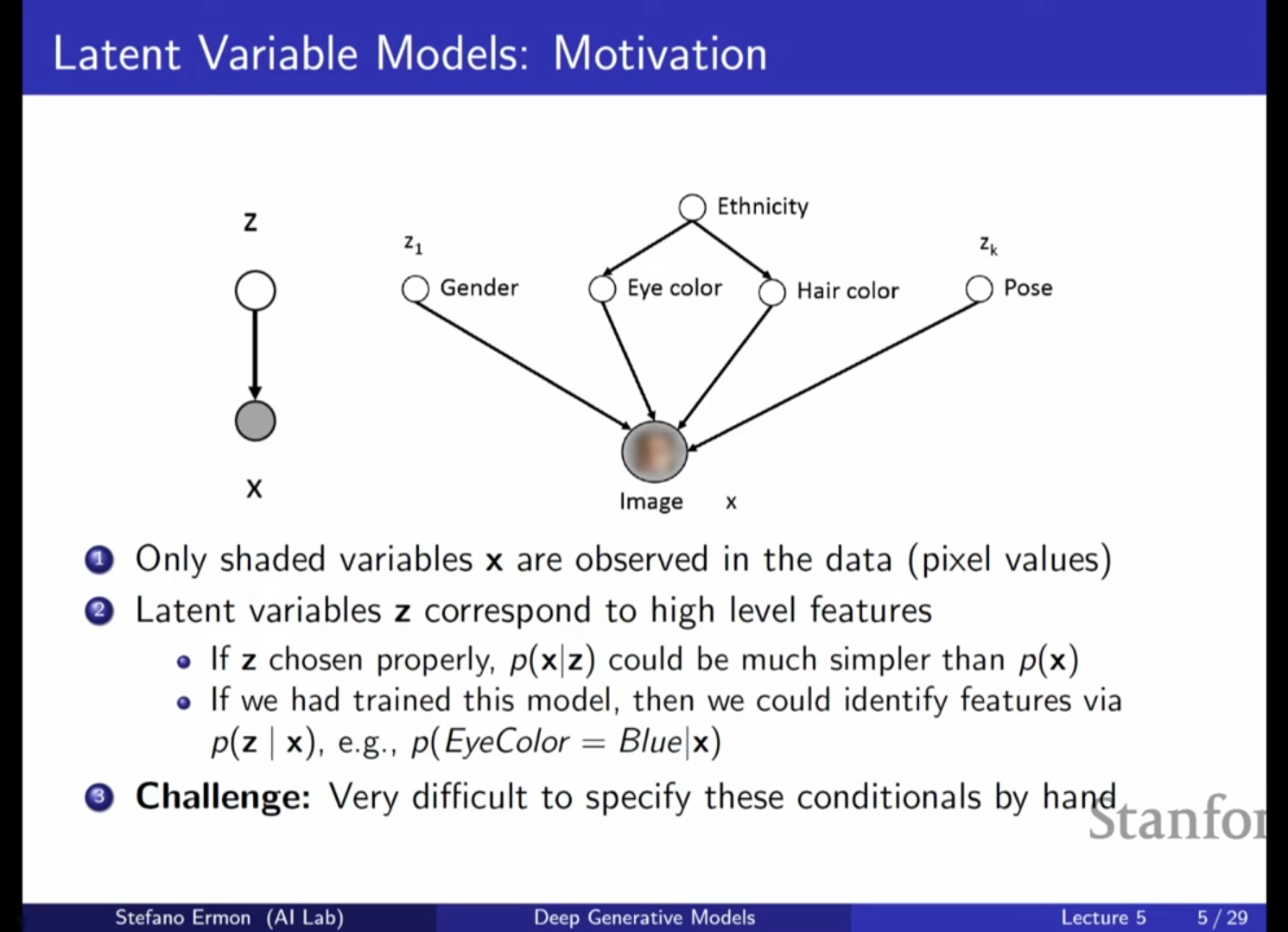
3. 심층 잠재 변수 모델 (Deep Latent Variable Models)

• 가우시안 가정: 잠재 변수 $z$가 단순한 가우시안 분포(Gaussian Distribution)를 따른다고 가정합니다.
• 신경망을 통한 모델링: $x$와 $z$ 사이의 복잡하고 해석 불가능한 관계를 심층 신경망(Deep Neural Networks)을 통해 학습합니다.
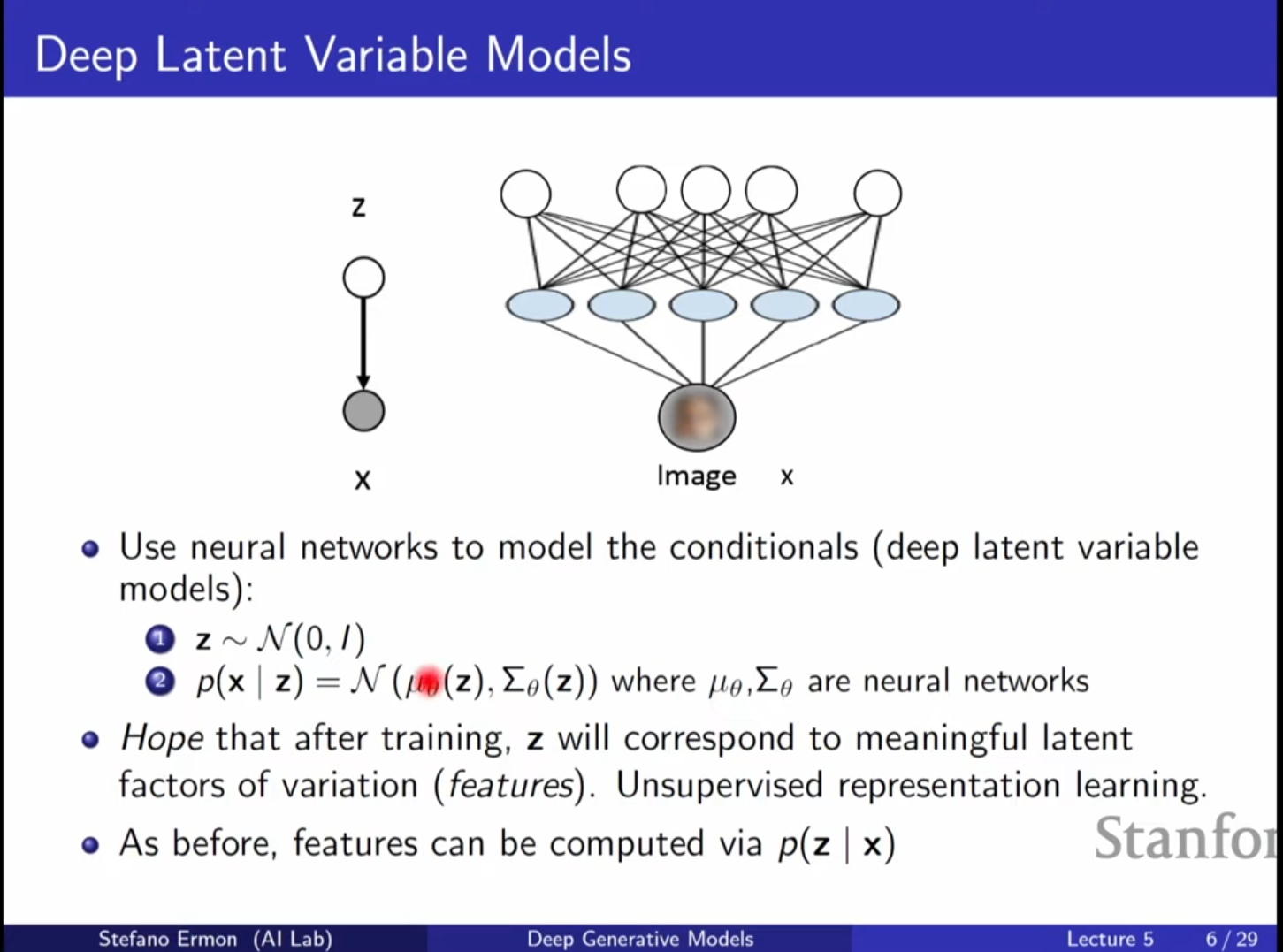
• 수학적 구성:
  • $P(z) = \mathcal{N}(0, I)$ (단순한 사전 분포)
  • $P(x|z) = \mathcal{N}(\mu_\theta(z), \Sigma_\theta(z))$
  • 여기서 $\mu_\theta(z)$와 $\Sigma_\theta(z)$는 $z$를 입력으로 받아 평균과 공분산을 출력하는 신경망입니다.
• 심화 내용: 기술적 배경 및 한계:
  • 기술적 배경: $P(x|z)$ 자체는 단순한 가우시안일지라도, 신경망을 통해 파라미터가 결정되므로 전체 모델은 매우 복잡한 데이터 분포를 근사할 수 있습니다.
  • 명확한 한계점: 무감독 학습의 특성상 학습된 잠재 변수 $z$가 반드시 인간이 이해할 수 있는 의미(예: 나이, 성별)를 가질 것이라는 보장은 없습니다.

---

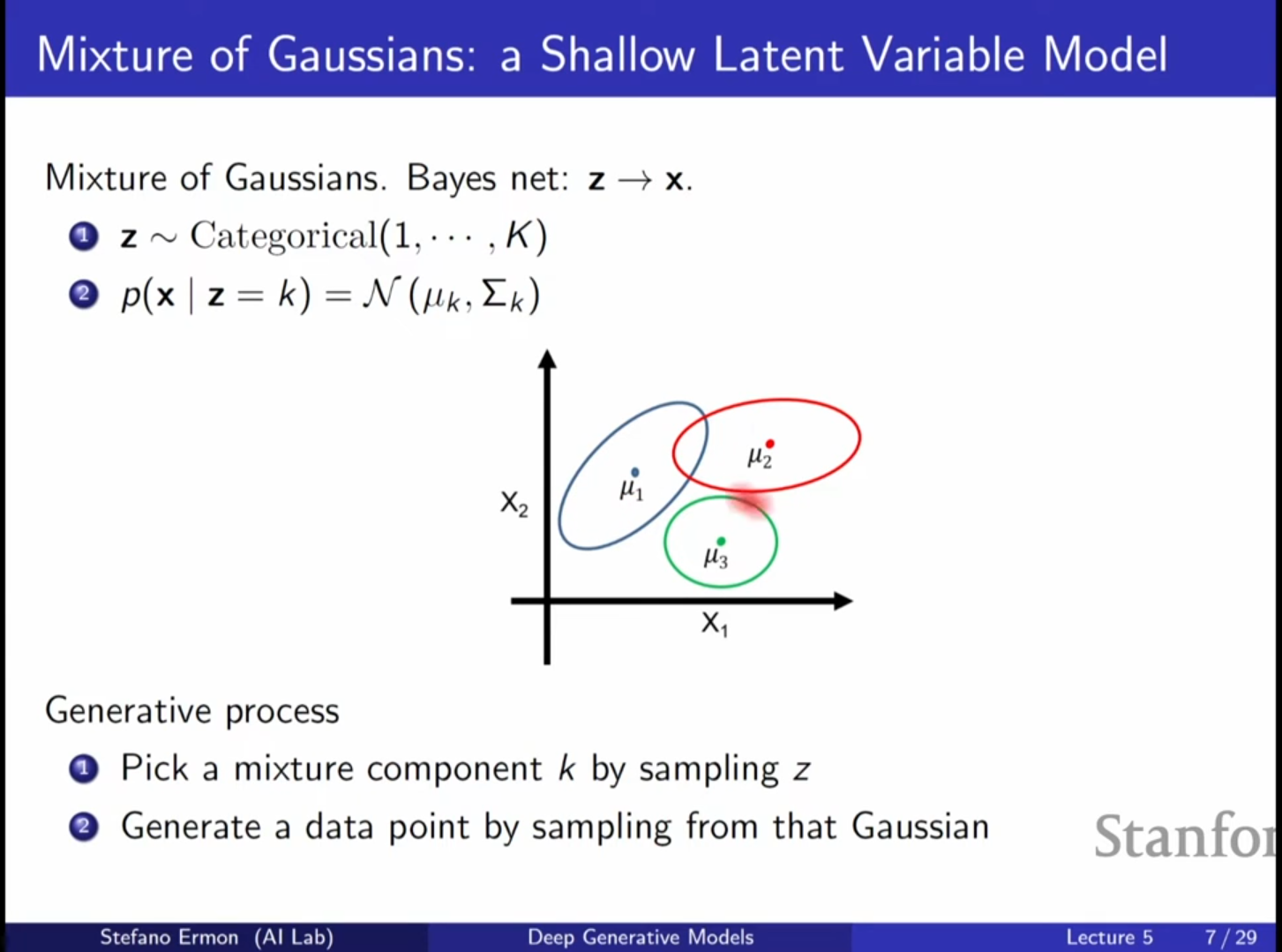
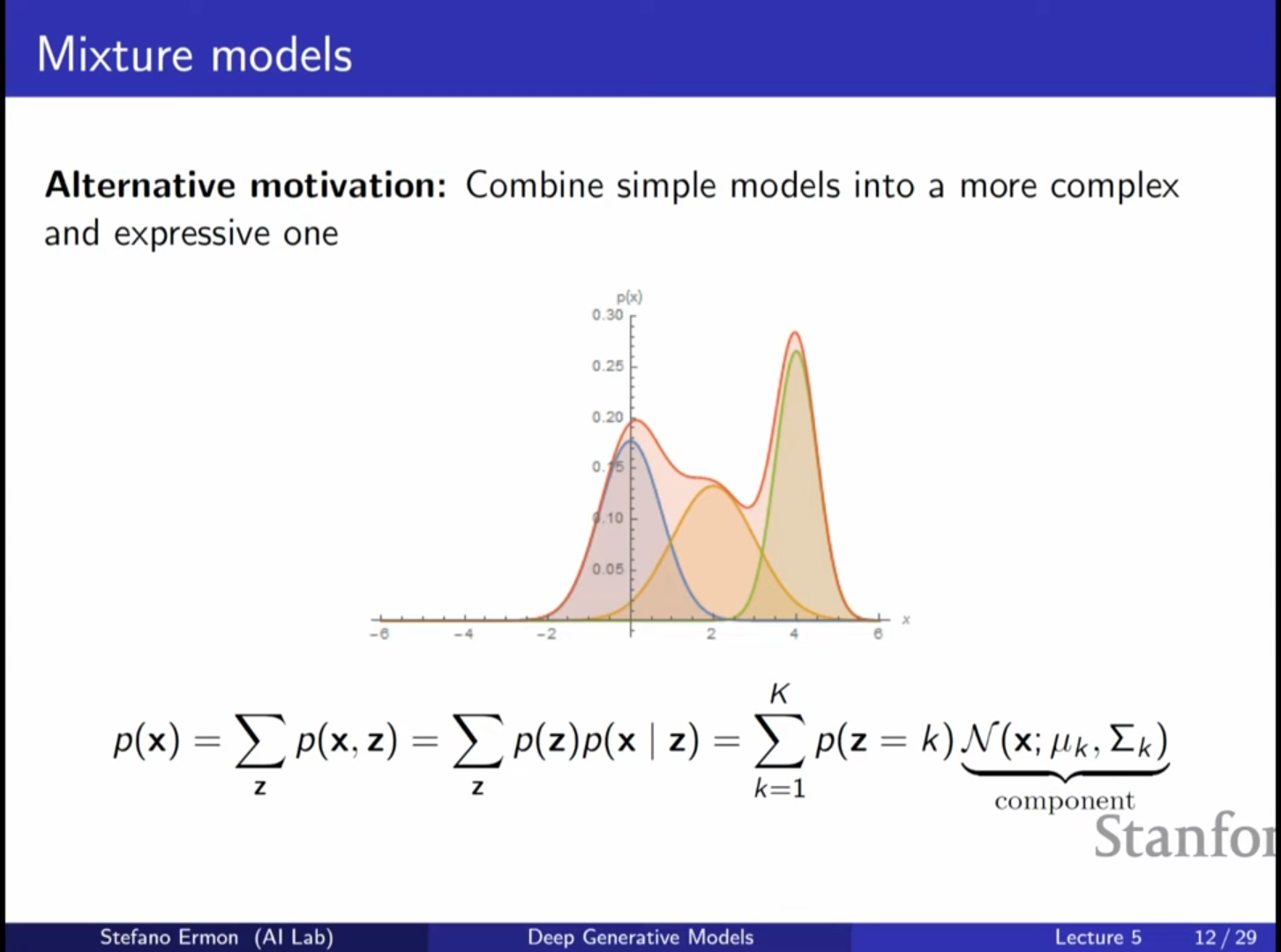
4. 얕은 모델의 예시: 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)

• 개념: $z$가 범주형 변수(Categorical Variable)인 가장 단순한 형태의 잠재 변수 모델입니다.
• 작동 방식: 먼저 어떤 혼합 성분(Component) $z$를 선택할지 결정하고, 해당 성분에 해당하는 가우시안 분포에서 $x$를 샘플링합니다.
• Yellowstone National Park 예시: 간헐천 분출 데이터(Old Faithful geyser)를 하나의 가우시안으로 모델링하면 데이터가 없는 영역에도 높은 확률을 부여하는 등 성능이 낮지만, 두 개의 가우시안 혼합으로 모델링하면 훨씬 정확하게 데이터의 구조를 캡처할 수 있습니다.

---

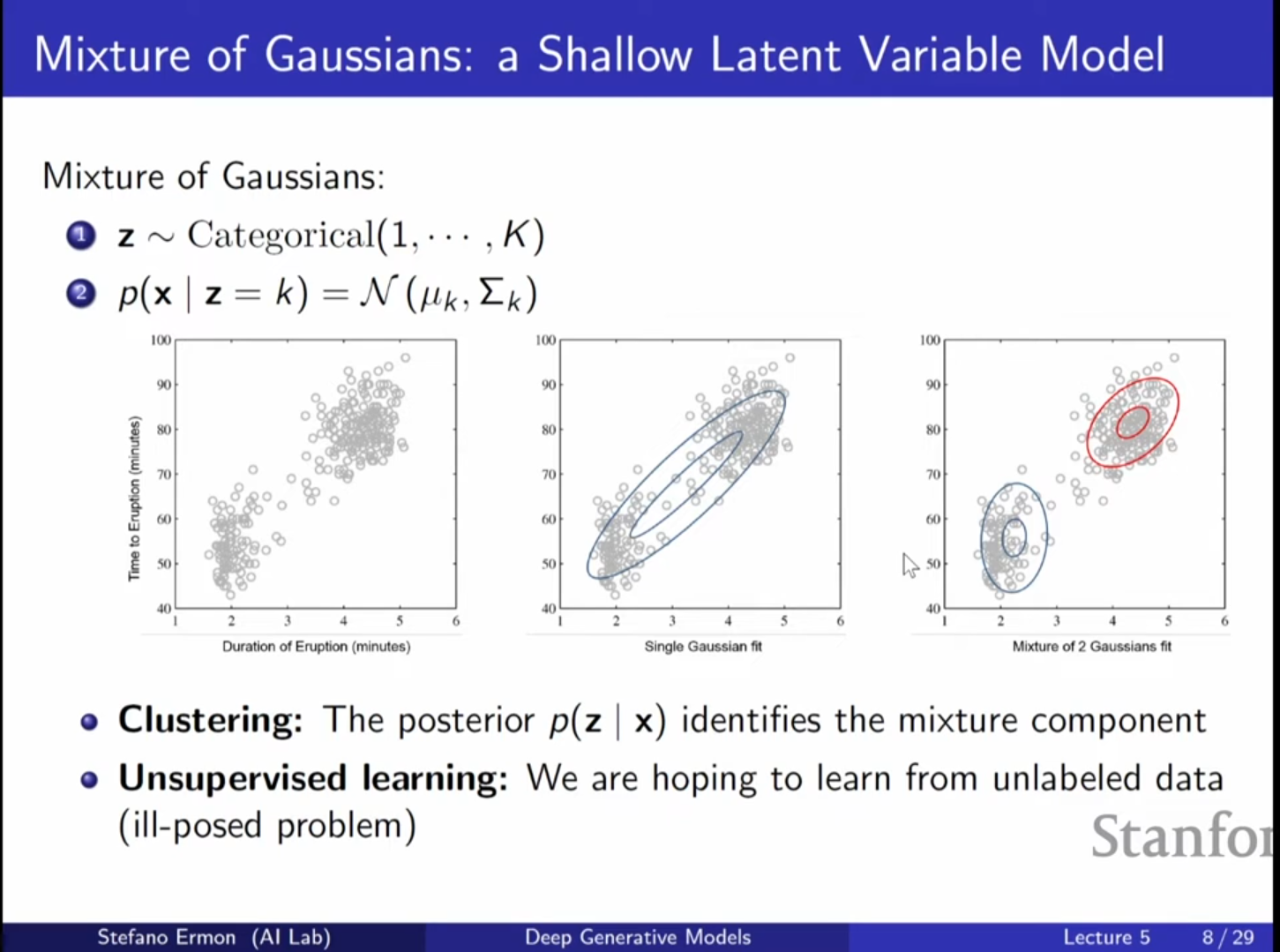
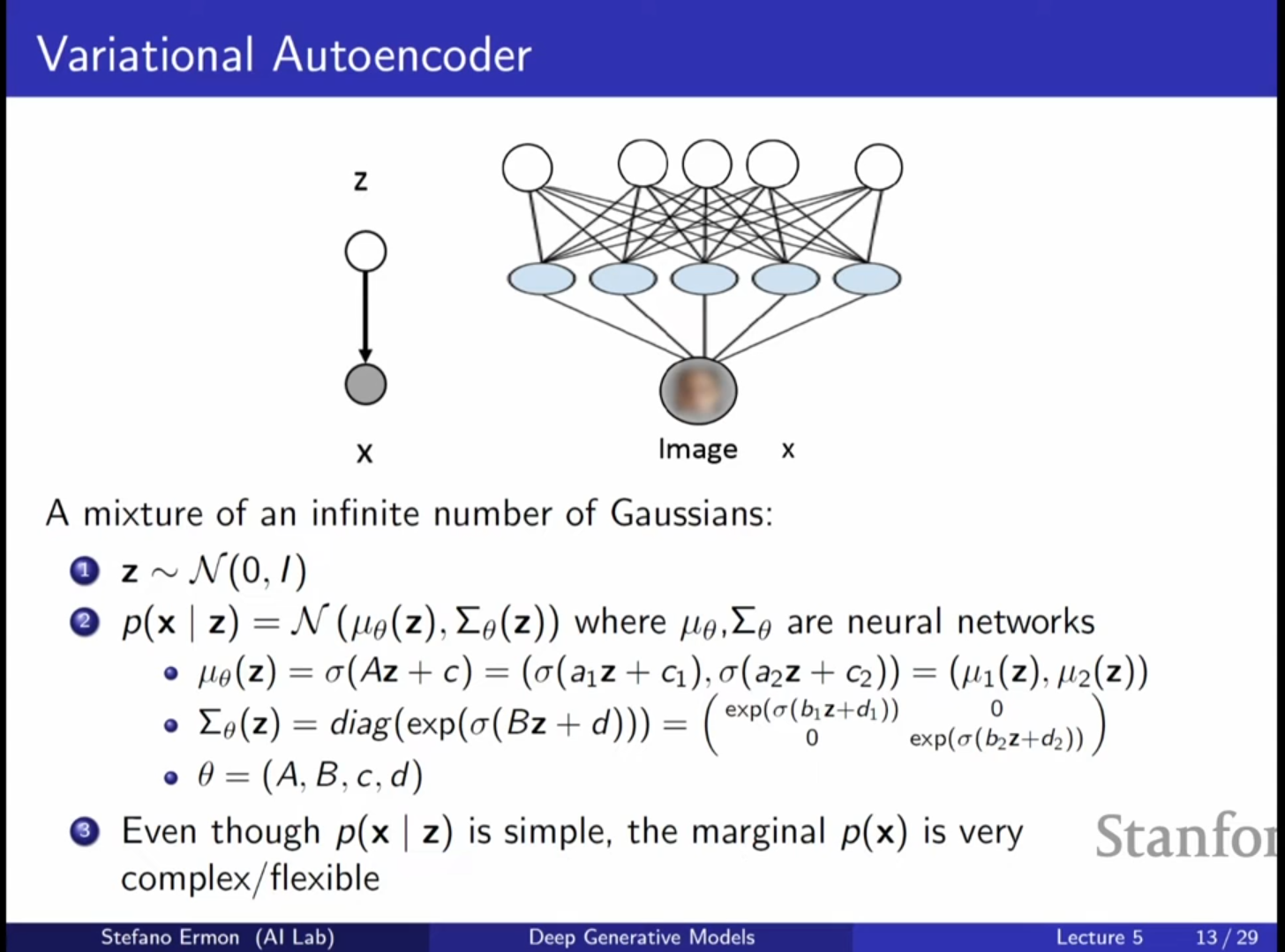
5. VAE: 무한한 혼합 모델 (Infinite Mixture Model)

• 연속적 잠재 공간: GMM이 유한한 $K$개의 혼합 성분을 갖는 것과 달리, VAE는 $z$를 연속적인 가우시안 분포에서 샘플링하므로 무한한 개수의 가우시안 혼합 모델로 해석할 수 있습니다.
• 샘플링 과정:
  1. 사전 분포 $P(z)$에서 $z$를 샘플링합니다.
  2. $z$를 신경망에 통과시켜 $\mu$와 $\sigma$를 얻습니다.
  3. $P(x|z)$ 가우시안 분포에서 $x$를 샘플링합니다.
  

---

6. 주변 우도($P(x)$) 계산의 난제와 해결 시도

• 왜 주변 우도 $P(x)$를 최대화하려는가?

  • 생성 모델의 목표는 관측 데이터 $x$가 모델로부터 얼마나 그럴듯하게 생성될 수 있는지를 평가하는 것입니다.
  • 잠재 변수 $z$는 관측되지 않으므로, 모든 가능한 $z$를 적분으로 제거한 주변 우도 $P(x)$를 기준으로 모델을 학습합니다.
  • 따라서 잠재 변수 모델에서도 학습 목표는 $\log P(x)$를 최대화하는 것입니다.

• 주변 우도(Marginal Likelihood) 계산의 어려움

  • 모델을 학습시키려면 $P(x)$를 계산해야 하며, 이는 모든 가능한 $z$에 대해 적분(Marginalization)해야 함을 의미합니다.
  • 수식:
    $P(x) = \int P(x, z)\,dz$
  • 잠재 변수 $z$가 고차원일 경우, 이 적분은 수치적으로 계산이 거의 불가능합니다.
  • 이는 고차원 공간에서 발생하는 차원의 저주(Curse of Dimensionality) 문제 때문입니다.

• Posterior와의 연결

  • Bayes Rule에 따르면 posterior는 다음과 같이 정의됩니다.
    $P(z|x) = \frac{P(x,z)}{P(x)}$
  • 즉, $x$를 생성했을 가능성이 높은 $z$를 알고 싶다면 $P(z|x)$가 필요합니다.
  • 그러나 $P(z|x)$를 계산하려면 분모에 $P(x)$가 필요하므로, 주변 우도 계산 문제는 곧 posterior 추론 문제로 이어집니다.

• 직관적 비유 (결측치 유추)

  • 이미지의 절반이 가려진 경우, 가능한 모든 픽셀 조합을 전부 시도해 보고 평균을 내는 것은 매우 비효율적입니다.
  • 주변 우도 계산 역시 이와 유사한 비효율을 가집니다.

6-1. 첫 번째 시도: 균등 분포 몬테카를로 샘플링 (실패)

• 방법: 모든 가능한 $z$의 집합에서 균등 분포(Uniform Distribution)로 $K$개의 샘플을 무작위로 뽑아 평균을 내는 방식입니다.
• 수식: $P(x) \approx \frac{|Z|}{K} \sum_{k=1}^K P(x, z^{(k)})$.
• 한계: 이론적으로는 편향되지 않았으나(Unbiased), 대부분의 무작위 $z$는 $x$를 생성할 확률이 0에 가깝습니다. 이로 인해 분산(Variance)이 너무 커서 실질적으로 학습이 불가능합니다.

6-2. 두 번째 시도: 중요도 샘플링 (Importance Sampling)

• 방법: $x$를 잘 설명할 수 있는 '중요한' $z$를 더 자주 뽑기 위해 임의의 제안 분포 $Q(z)$를 도입합니다.
• 수식: $P(x) = \int Q(z) \frac{P(x, z)}{Q(z)} dz = \mathbb{E}_{z \sim Q} [\frac{P(x, z)}{Q(z)}]$.
• 샘플 기반 근사: $P(x) \approx \frac{1}{K} \sum_{k=1}^K \frac{P(x, z^{(k)})}{Q(z^{(k)})}$ (단, $z^{(k)} \sim Q$).
• 문제: 우리가 원하는 것은 $\log P(x)$인데, 기댓값에 로그를 취하면($\log \mathbb{E}[\cdot]$) 편향이 발생하여 직접적인 최적화가 어렵습니다.

---

7. 변분 추론 및 ELBO (Evidence Lower Bound)

• 변분 추론의 핵심 아이디어

  • 직접 계산할 수 없는 posterior $P(z|x)$ 대신,
  • 이를 근사하는 분포 $Q(z|x)$를 도입하여 문제를 해결합니다.
  • 변분 추론은 $\log P(x)$의 계산 가능한 하한선을 최대화하는 방식입니다.

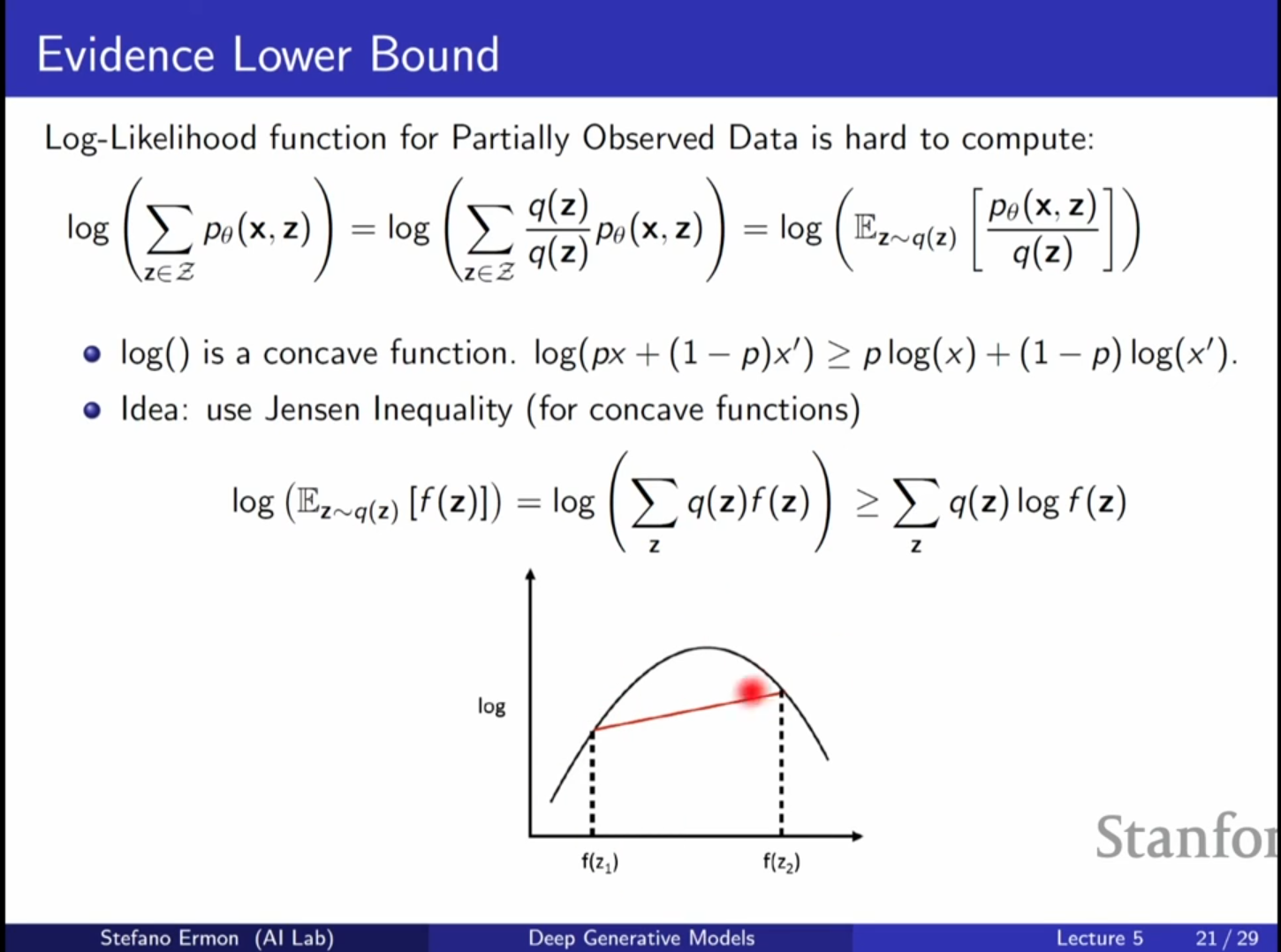
• 젠센의 부등식(Jensen’s Inequality) 적용

  • 로그 함수는 오목 함수이므로 다음이 성립합니다.
    $\log P(x) = \log \mathbb{E}_{z \sim Q}\left[\frac{P(x,z)}{Q(z)}\right] \geq \mathbb{E}_{z \sim Q}\left[\log \frac{P(x,z)}{Q(z)}\right]$

• ELBO (Evidence Lower Bound)

  • 위 식의 우변을 ELBO라고 부릅니다.
    $\text{ELBO} = \mathbb{E}_{z \sim Q}[\log P(x,z) - \log Q(z)]$
  • $\log P(x)$를 직접 계산하는 대신, 이 하한선을 최대화합니다.

• ELBO와 Posterior의 관계

  $\log P(x) = \text{ELBO} + \text{KL}(Q(z|x)\,\|\,P(z|x))$
  • KL Divergence는 항상 0 이상이므로 ELBO는 항상 로그 우도의 하한선이 됩니다.
  • $Q(z|x) = P(z|x)$일 때 ELBO와 $\log P(x)$는 동일해집니다.

• VAE로의 연결

  • VAE에서는 $Q(z|x)$를 인코더 신경망으로 모델링하고,
  • $P(x|z)$를 디코더 신경망으로 모델링하여 ELBO를 최대화합니다.

---

8. Q&A (강의 중 질의응답)

• Q: $z$의 차원은 어떻게 결정하나요?
  • A: $z$의 차원은 하이퍼파라미터이며, 일반적으로 관찰 데이터 $x$의 차원보다 훨씬 낮게 설정하여 핵심적인 가변 요소를 추출하도록 유도합니다.
• Q: 이 모델은 종단간 미분(End-to-end differentiable)이 가능한가요?
  • A: 샘플링 과정이 포함되어 있어 미분이 어렵지만, 다음 강의에서 다룰 재파라미터화 트릭(Reparameterization trick)을 통해 해결할 수 있습니다.
• Q: 사전 분포 $P(z)$를 학습 중에 업데이트할 수 있나요?
  • A: 가능합니다. 기본적으로는 고정된 가우시안을 사용하지만, 더 복잡한 사전 분포를 학습하는 모델도 존재합니다.
• Q: 잠재 변수가 독립적이라는 것을 어떻게 보장하나요?
  • A: 이를 위해 독립성을 강제하는 얽힘 해제 표현 학습(Disentangled representation learning) 분야가 활발히 연구되고 있지만, 이론적으로는 일반적인 경우에 불가능하다는 증명도 있습니다.

---

💡 비유를 통한 요약:
잠재 변수 모델을 만드는 것은 마치 '수많은 화풍(z)을 가진 화가(DNN)'를 고용하는 것과 같습니다. 우리는 화가가 어떤 화풍을 선택했는지($z$)는 모르지만, 완성된 그림($x$)들을 보고 "이 화가는 아마 이런 화풍들을 가지고 있겠구나"라고 추측하며 화가를 훈련시킵니다. 이때 모든 화풍을 일일이 확인하는 것은 불가능하므로, ELBO라는 최소한의 기준선을 설정해 화가를 효율적으로 교육하는 것입니다.