[CV] CS236 6강 정리 [VAEs]

1. Variational Autoencoder (VAE)의 기초와 생성 과정

• VAE의 정의: 단순한 잠재 변수(Latent Variable) 모델을 신경망을 통해 매우 유연한 생성 모델로 확장한 형태입니다.
• 데이터 생성 프로세스:
  1. 잠재 변수 $Z$ 샘플링: 단순한 분포(예: 평균이 0이고 공분산이 단위 행렬인 다변량 가우시안 분포, $P(Z)$)에서 $Z$를 추출합니다.
  2. 신경망 통과: 샘플링된 $Z$를 두 개의 신경망 $\mu_\theta(Z)$와 $\sigma_\theta(Z)$에 입력합니다.
  3. 데이터 샘플링: 신경망에서 나온 출력값(평균과 공분산)을 파라미터로 하는 또 다른 가우시안 분포 $P(X|Z)$에서 실제 데이터 $X$를 생성합니다.
• 유연성: 각각의 구성 요소(Prior, Conditional)는 단순한 가우시안이지만, 무한한 수의 가우시안을 혼합(Mixture)하는 효과를 내기 때문에 주변 확률 분포 $P(X)$는 매우 복잡하고 유연해질 수 있습니다.
• 비지도 학습: VAE는 $X$가 주어졌을 때 $Z$를 추론함으로써 데이터 내의 숨겨진 구조나 변화의 요인을 발견하는 데 사용됩니다.
• 심화 내용 - VAE의 기술적 배경: VAE는 K-means의 확장판으로 간주할 수 있습니다. K-means가 단순한 군집을 찾았다면, VAE는 더 복잡하고 유연한 잠재 변수를 통해 데이터의 변동성을 설명합니다. 다만, 유연함의 대가로 우도(Likelihood)를 평가하는 비용이 매우 비싸다는 한계가 존재합니다.

---

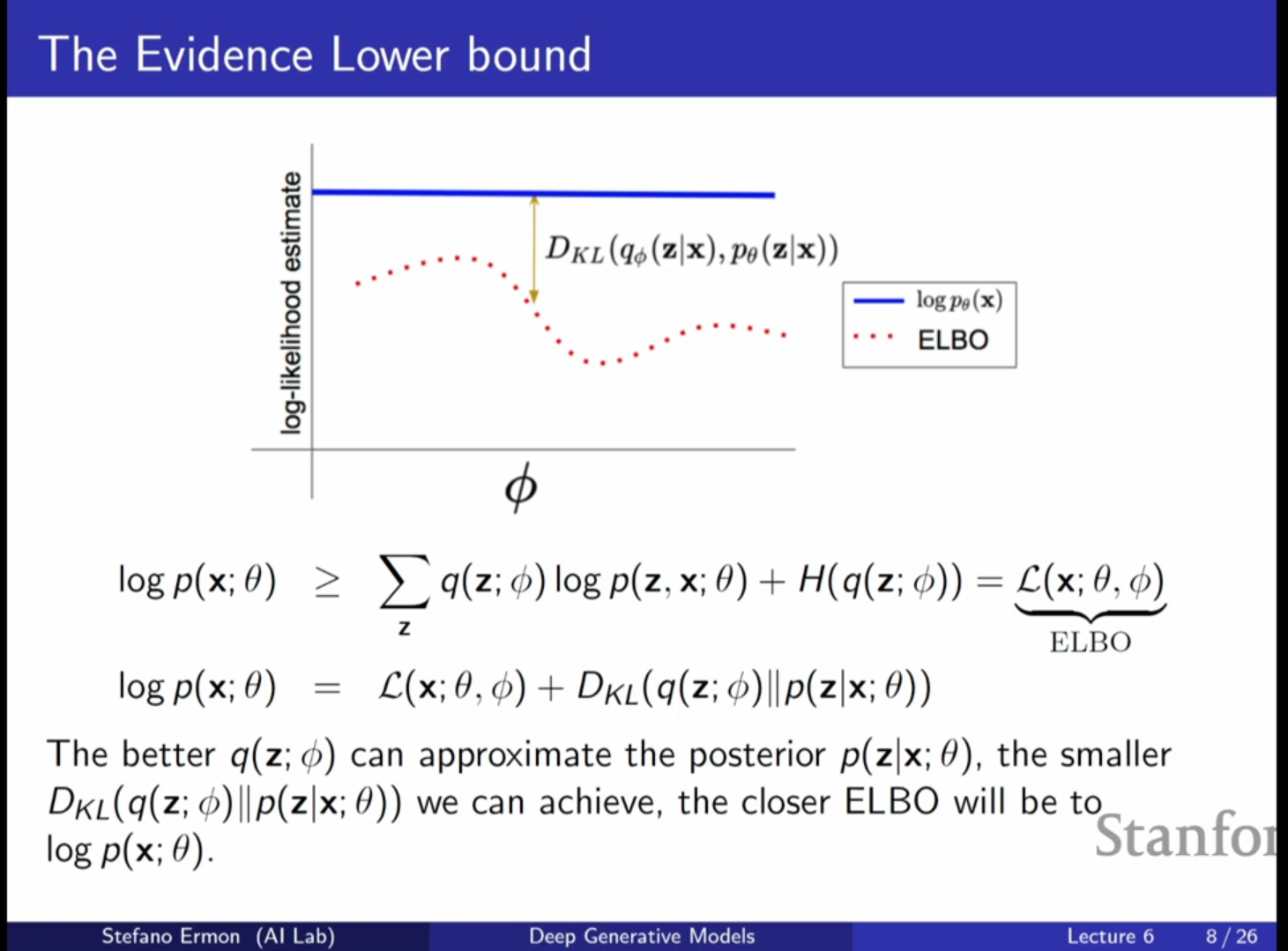
2. Evidence Lower Bound (ELBO)의 유도와 의미

• 학습의 난제: $P(X)$를 직접 최적화하려면 모든 $Z$에 대해 적분해야 하는데, 이는 계산적으로 불가능(Intractable)합니다.
• 변분 추론(Variational Inference): $P(Z|X)$를 직접 구할 수 없으므로, 이를 근사하는 보조 모델 $Q(Z|X)$를 도입합니다.
• ELBO의 수학적 유도:
  • Jensen's Inequality를 사용하여 로그 우도($\log P(X)$)의 하한선을 구합니다.
  • KL Divergence를 이용한 또 다른 유도 방식은 $KL(Q(Z|X) || P(Z|X))$가 항상 0 이상이라는 점을 이용하는 것입니다.
• ELBO의 두 가지 구성 요소:
  1. Reconstruction Term: $Q$를 통해 추론된 $Z$를 기반으로 데이터를 얼마나 잘 복원하는지를 나타내는 평균 로그 확률입니다.
  2. Entropy Term: $Q$ 분포가 얼마나 무작위한지를 나타내는 엔트로피입니다.
• 최적의 $Q$: $Q(Z|X)$가 실제 사후 분포인 $P(Z|X)$와 정확히 일치할 때 ELBO는 실제 로그 우도와 같아집니다(Tight bound).
• 심화 내용 - ELBO의 한계: 이상적으로는 $Q$를 실제 사후 분포로 선택하고자 하지만, 사후 분포를 계산하는 것 자체가 $P(X)$를 구하는 것만큼 어렵기 때문에 최적화를 통해 최대한 가까운 $Q$를 찾으려 노력하게 됩니다.
  

---

3. VAE의 최적화와 훈련 전략

• 공동 최적화(Joint Optimization): 생성 모델의 파라미터 $\theta$와 추론 모델의 파라미터 $\phi$를 동시에 최적화합니다.
  • $\theta$를 최적화하여 하한선 자체를 높입니다.
  • $\phi$를 최적화하여 하한선을 실제 값에 최대한 밀착시킵니다.
• 이미지 보정 예시: 이미지의 하단 절반($X$)만 보일 때 누락된 상단 절반($Z$)을 추론하는 상황에서, 단순히 무작위로 픽셀을 채우는 것보다 관찰된 데이터를 기반으로 일관성 있는 상단 데이터를 추측하는 것이 좋은 $Q$를 선택하는 과정이 됩니다.
• 훈련 알고리즘: 데이터 포인트를 샘플링하고, 해당 데이터에 대한 ELBO의 그래디언트를 계산한 뒤, $\theta$와 $\phi$를 업데이트하여 ELBO를 최대화합니다.

---

4. Reparameterization Trick (재매개변수화 트릭)

• 문제점: 샘플링은 확률적(무작위적)인 행위이므로(똑같은 평균과 표준편차를 주어도 다른 결과값(z)가 나오는 행위이므로, 즉, 함수가 아니므로) 수학적으로 미분 불가능합니다. 샘플링 과정 $Q_\phi$가 파라미터 $\phi$에 직접 의존하면, 샘플링 노드에서 그래디언트의 흐름이 끊겨 역전파를 통해 파라미터를 업데이트할 수 없게 됩니다.
• 해결책: 확률적인 노드를 미분 가능한 형태로 만들기 위해 무작위성을 파라미터와 분리합니다. 즉, 샘플링 과정을 결정론적인 함수와 외부 노이즈의 조합으로 재정의합니다. (샘플링의 무작위성을 $\epsilon$에게 부여해서 나머지를 함수로 정해지게 합니다.)
• 수식: $Z = \mu_\phi(X) + \sigma_\phi(X) \odot \epsilon$ (여기서 $\epsilon \sim N(0, I)$)
• 장점: 모든 무작위성이 파라미터 $\phi$와 무관한 외부 노이즈 $\epsilon$으로 옮겨집니다. 결과적으로 $Z$는 $\mu$와 $\sigma$에 대한 미분 가능한 함수가 되어, 신경망 전체에 대해 오차 역전파(Backpropagation)가 가능해집니다.
  

---

5. Amortized Inference (상각 추론)

• 개념: 데이터 포인트마다 개별적인 최적의 파라미터를 찾는 대신, 모든 데이터에 공통으로 적용되는 하나의 신경망(Encoder)을 학습시킵니다.
• 효과: 새로운 데이터가 들어왔을 때 별도의 최적화 과정 없이 피드포워드 한 번으로 즉시 추론이 가능해져 매우 효율적입니다.
• 정규화 효과: 인코더를 통해 $P(Z|X)$를 학습하는 과정은 모델이 추론하기 쉬운 형태로 데이터를 생성하도록 유도하는 효과를 줍니다.

---

6. Q&A (질문 및 답변 내용 요약)

• Q: $P(Z)$(Prior)도 학습할 수 있습니까?
  • A: 네, 고정된 가우시안 대신 파라미터화된 분포를 사용하거나 계층적 구조를 통해 학습할 수 있으며, 이는 Diffusion Model과도 연결되는 개념입니다.
• Q: 신경망의 층을 깊게 하는 것과 $Z$의 차원을 높이는 것 중 무엇이 더 유연합니까?
  • A: 둘 다 유연성을 높이지만, 층을 쌓거나 차원을 조절하는 것은 혼합 성분(Mixture components)을 추가하여 복잡한 분포를 표현하는 효과를 줍니다.
• Q: 추론 시에도 Encoder가 필요합니까?
  • A: 단순 생성 시에는 Decoder만 사용하지만, 데이터의 우도 평가나 이상 탐지 시에는 Encoder가 반드시 필요합니다.

---

핵심 내용: VAE의 3가지 핵심 포인트

1. 유연한 생성: 단순한 가우시안 분포의 결합을 통해 복잡한 데이터 분포 $P(X)$를 모델링합니다.
2. ELBO 최적화: 직접 계산이 불가능한 로그 우도 대신, 하한선인 ELBO를 최대화하는 방식으로 학습합니다.
3. 학습 가능성: Reparameterization Trick을 통해 확률적 샘플링 과정을 미분 가능한 형태로 바꾸어 신경망 학습을 가능하게 합니다.

---