[CV] CS236 7강 정리 [Normalizing Flows]

김성윤(Jack)·2026년 1월 19일

CV

목록 보기

25/30

1. 변분 오토인코더(VAE)의 오토인코더적 해석

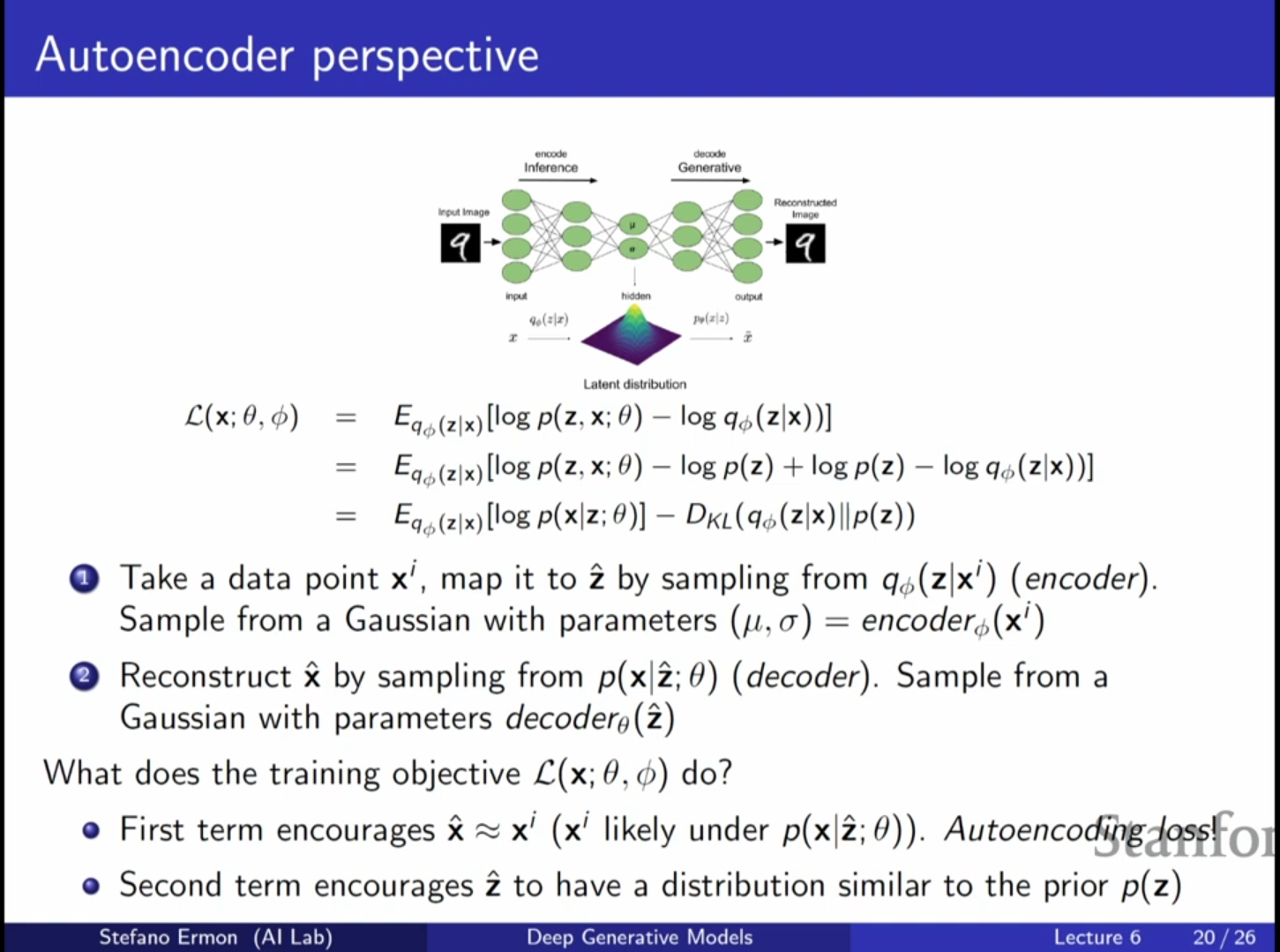
VAE의 훈련 목표와 오토인코더의 관계: 지난 강의에 이어 변분 오토인코더(VAE)를 오토인코더(Autoencoder)의 관점에서 해석하는 것으로 강의를 시작합니다. VAE의 목적 함수인 ELBO(Evidence Lower Bound)는 두 부분으로 나눌 수 있으며, 첫 번째 부분은 재구성(Reconstruction) 손실, 두 번째 부분은 정규화(Regularization) 항으로 해석됩니다.
첫 번째 항: 재구성 손실 (Autoencoding Loss):
- 이 항은 데이터 $x$ 를 인코더 $q$ 에 통과시켜 잠재 변수 $z$ 를 얻고, 이를 다시 디코더 $p$ 에 통과시켰을 때 원래 데이터 $x$ 가 얼마나 잘 복원되는지를 측정합니다.
- $p(x|z)$ 가 가우시안 분포라면, 이는 입력과 출력 사이의 L2 손실(Loss)과 유사하게 작동하며, 입력을 잠재 벡터로 매핑했다가 다시 입력으로 되돌리는 오토인코더의 특성을 가집니다.
- 일반적인 오토인코더가 결정론적(deterministic)인 것과 달리, VAE는 입력을 잠재 변수들의 분포로 매핑하는 확률적(stochastic) 오토인코더입니다.
두 번째 항: 정규화 (Regularization via KL Divergence):
- 인코더가 생성한 잠재 변수의 분포 $q(z|x)$ 와 사전 분포 $p(z)$ (주로 가우시안) 사이의 KL 발산(KL Divergence)을 최소화하는 항입니다.
- 이 항은 잠재 변수들이 사전 분포인 가우시안 형태를 띠도록 강제합니다.
- 만약 첫 번째 항만 최적화한다면 단순한 오토인코더가 되어 새로운 데이터를 생성할 수 없지만, 이 두 번째 항 덕분에 우리는 사전 분포에서 $z$ 를 샘플링하여 디코더를 속이고 그럴듯한 데이터를 생성할 수 있게 됩니다.

심화 내용: 생성 모델로서의 VAE: VAE가 일반적인 오토인코더와 다른 점은 생성 능력에 있습니다. 훈련 중에는 데이터에서 $z$ 를 얻지만, 생성 시(Inference time)에는 인코더를 무시하고 사전 분포 $p(z)$ 에서 직접 $z$ 를 샘플링합니다. KL 발산 항은 인코더가 생성하는 $z$ 의 분포가 사전 분포와 유사하도록 만들어주므로, 사전 분포에서 샘플링한 $z$ 도 디코더를 통과했을 때 유의미한 데이터를 생성하게 됩니다.

2. 정보 압축과 VAE의 직관적 예시 (앨리스와 밥)

우주비행사 앨리스의 통신 예시: VAE의 작동 원리를 설명하기 위해 우주에 있는 앨리스가 지구에 있는 밥에게 이미지를 전송하는 상황을 가정합니다.
- 앨리스 (인코더): 이미지를 전송하기에 대역폭이 부족하여 이미지를 압축된 표현 $z$ (예: 1비트 또는 하나의 실수)로 변환하여 보냅니다.
- 밥 (디코더): 받은 메시지 $z$ 를 통해 원래 이미지를 복원하려고 시도합니다.
손실 함수의 의미:
- 재구성 손실이 낮다는 것은 밥이 받은 메시지로 원래 이미지를 잘 복원했다는 의미입니다.
- $z$ 가 매우 제한적(예: 1비트)이라면 앨리스는 비슷한 이미지들을 클러스터링하여 같은 코드로 매핑해야 합니다(예: 개가 있는 사진은 0, 고양이는 1). 이는 모델이 데이터의 의미 있는 특징(Feature)을 발견하도록 유도합니다.
메시지 생성의 자율성: KL 발산 항이 작다는 것은 앨리스가 보내는 메시지의 분포가 사전 분포와 유사하다는 뜻입니다. 이는 밥이 앨리스로부터 메시지를 받지 않아도, 스스로 사전 분포에서 메시지를 샘플링하여 앨리스가 보냈을 법한 이미지를 생성할 수 있음을 의미합니다.

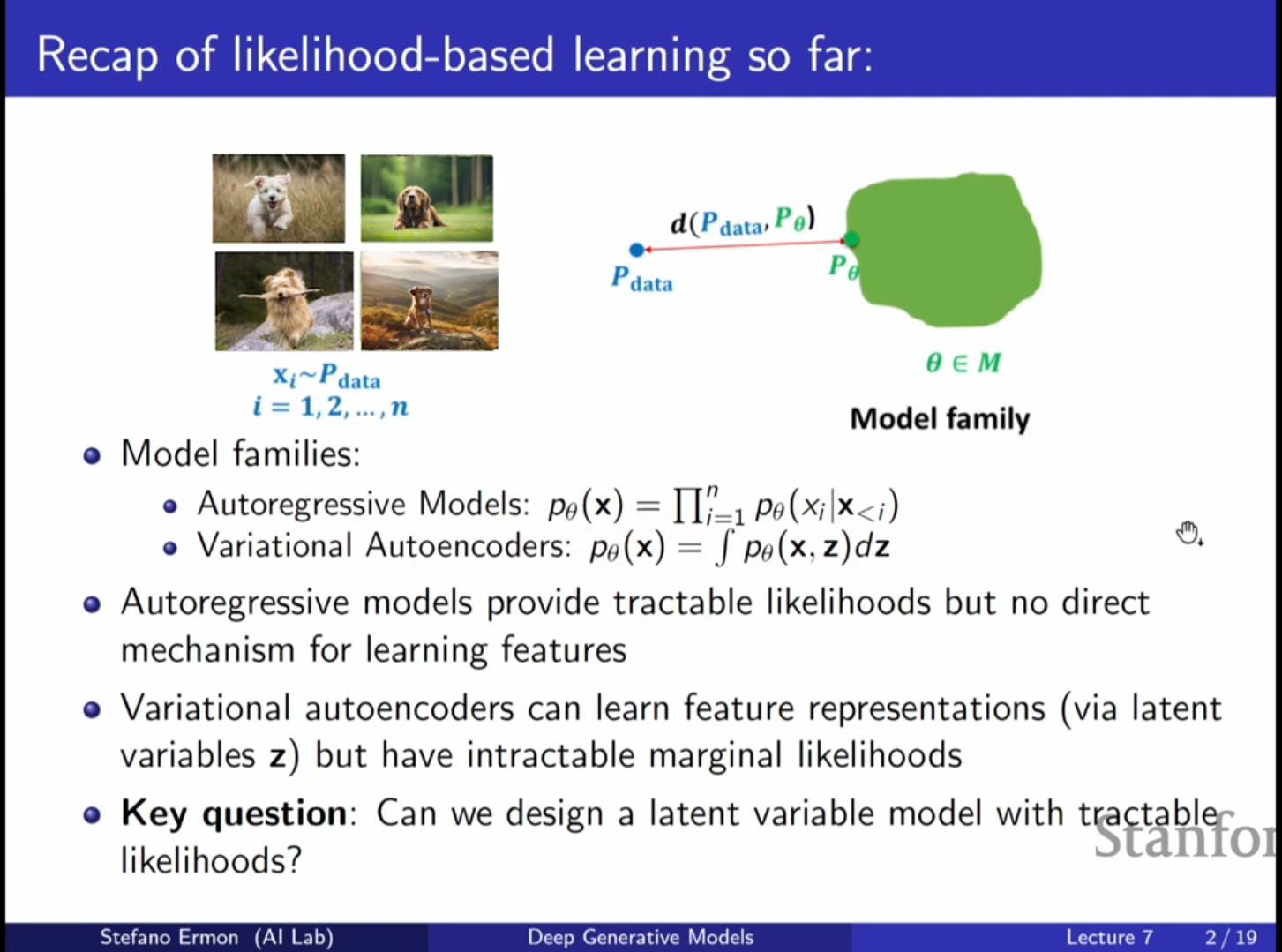
3. 노말라이징 플로우 (Normalizing Flows) 모델의 개요

플로우 모델의 등장 배경: VAE는 잠재 변수의 사후 분포를 다루기 위해 근사(Approximation)와 ELBO를 사용해야 했고, 주변부 우도(Marginal Probability)를 직접 계산하기 어려웠습니다. 플로우 모델(Flow Models)은 잠재 변수 모델이면서도 변분 추론 없이 우도를 직접 계산하고 최대 우도(Maximum Likelihood)로 훈련할 수 있는 모델입니다.
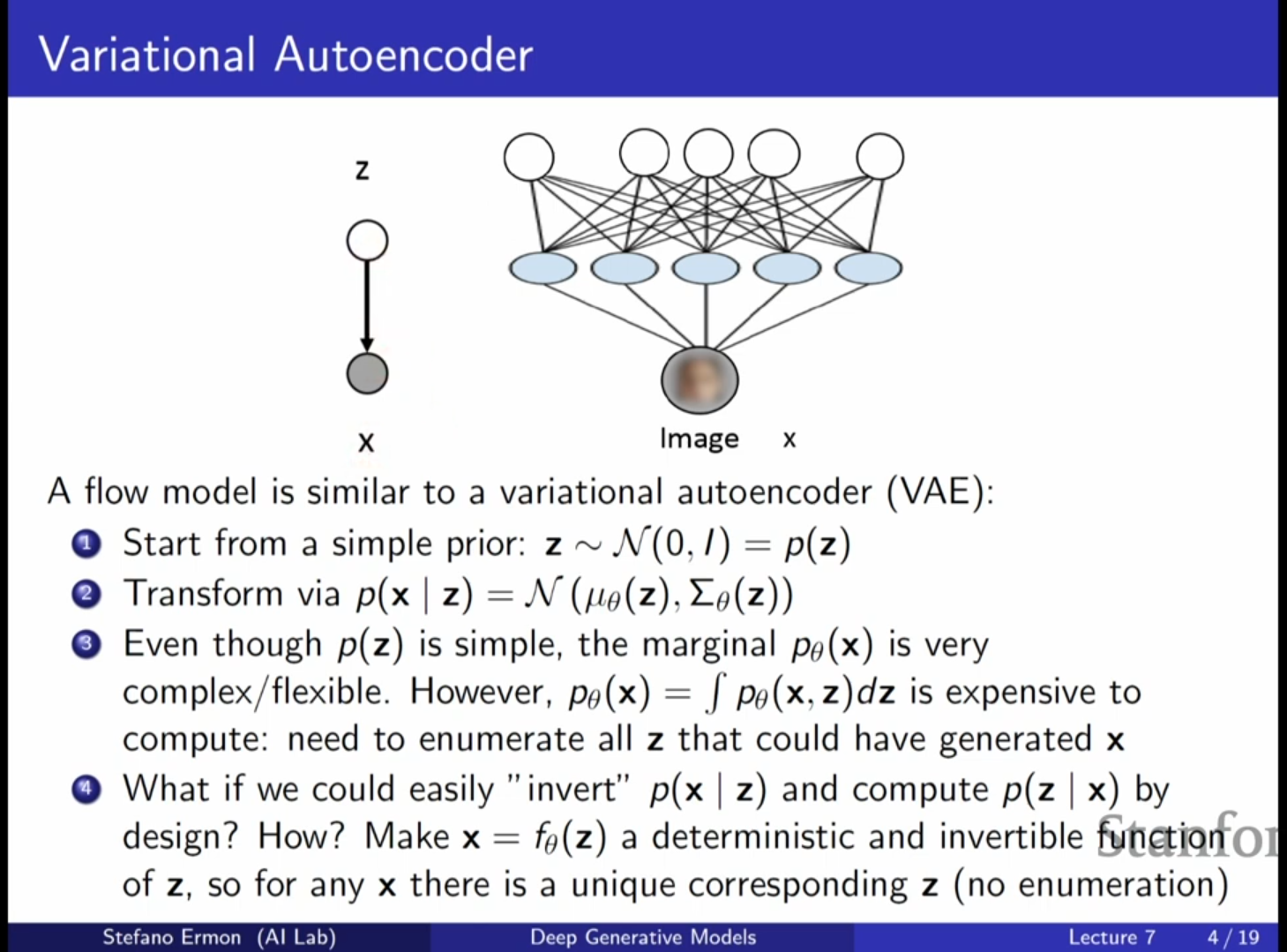
핵심 아이디어:
- 간단한 분포(가우시안, 균등 분포 등)에서 샘플링한 변수 $z$ 에 역변환 가능한(Invertible) 함수들을 연속적으로 적용하여 복잡한 데이터 분포 $p(x)$ 를 모델링합니다.
- VAE와 달리 $z$ 에서 $x$ 로 가는 매핑이 결정론적(deterministic)이고 역변환 가능합니다.
- 주어진 $x$ 에 대해 이를 생성한 $z$ 를 유일하게 찾을 수 있으므로 추론이 용이합니다.
제약 사항: 역변환이 가능해야 하므로 잠재 변수 $z$ 와 데이터 $x$ 는 동일한 차원을 가져야 합니다. 즉, VAE처럼 차원 축소를 통한 정보 압축의 개념은 적용되지 않습니다.

4. 변수 변환 (Change of Variables) 공식

4.1. 1차원 변수 변환

기본 개념: 확률 변수 $z$ 를 함수 $f$ 를 통해 $x = f(z)$ 로 변환할 때, $x$ 의 확률 밀도 함수(PDF)를 구하는 방법입니다.
잘못된 접근: 단순히 $p_x(x) = p_z(f^{-1}(x))$ 라고 계산하면 적분했을 때 1이 되지 않아 확률 분포의 정의를 만족하지 못합니다.
올바른 공식: 변환 시 공간이 늘어나거나 줄어드는 비율을 보정하기 위해 도함수의 절댓값을 곱해줘야 합니다.
$p_x(x) = p_z(z) \left| \frac{dz}{dx} \right| = p_z(f^{-1}(x)) \left| (f^{-1})'(x) \right|$
여기서 $h = f^{-1}$ 일 때, 도함수 term은 $|h'(x)|$ 가 됩니다.
예시: $z \sim U$ 이고 $x = \exp(z)$ 인 경우, 역함수는 $\log(x)$ 이며 도함수는 $1/x$ 입니다. 이를 통해 $x$ 의 분포를 정확히 계산할 수 있습니다.

4.2. 다변수 선형 변환 (Multivariate Linear)

선형 변환: 벡터 $z$ 에 행렬 $A$ 를 곱하여 $x = Az$ 를 만드는 경우입니다.
기하학적 해석: 단위 초입방체(Hypercube)가 선형 변환에 의해 평행다면체(Parallelotope)로 변환됩니다. 이때 공간의 부피 변화율은 행렬 $A$ 의 행렬식(Determinant)에 해당합니다.
공식:
$p_x(x) = p_z(f^{-1}(x)) |\det(A)|^{-1} = p_z(W x) |\det(W)|$
여기서 $W = A^{-1}$ 입니다. 이 공식은 변환된 공간에서의 정규화를 보장하므로 '노말라이징(Normalizing)' 플로우라고 불립니다.

4.3. 비선형 변환과 신경망 (Nonlinear Transformations)

비선형 확장: $f$ 가 비선형 신경망인 경우, 국소적으로 선형화(Linearization)하여 생각할 수 있습니다. 이때 선형 변환의 행렬 $A$ 역할을 하는 것이 자코비안(Jacobian) 행렬입니다.
일반화된 공식:
$p_x(x) = p_z(f^{-1}(x)) \left| \det \left( \frac{\partial f^{-1}}{\partial x} \right) \right|$
또는 역함수 정리(Inverse function theorem)를 이용하여 순방향 매핑 $f$ 의 자코비안으로 표현할 수도 있습니다.
$p_x(x) = p_z(z) \left| \det \left( \frac{\partial f}{\partial z} \right) \right|^{-1}$
심화 내용: 계산 효율성: 임의의 신경망을 사용하면 역변환을 구하거나 자코비안의 행렬식(Determinant)을 계산하는 비용( $O(N^3)$ )이 매우 비쌉니다. 따라서 플로우 모델 연구의 핵심은 역변환이 쉽고 자코비안 행렬식 계산이 효율적인 특별한 구조의 신경망을 설계하는 것입니다.

5. 강의 중 질의응답 (Q&A)

Q1: 오토인코더는 훈련 데이터와 비슷한 이미지만 복원할 수 있는데, 어떻게 새로운 데이터를 생성하나요?
A1: 일반적인 오토인코더는 데이터 생성 프로세스를 시작할 방법이 없습니다. 하지만 VAE는 훈련 시 잠재 변수들이 사전 분포(가우시안)와 유사하게 분포하도록 정규화(KL 항)합니다. 따라서 생성 시에는 사전 분포에서 $z$ 를 샘플링하여 디코더에 입력함으로써, 마치 인코더에서 나온 것과 유사한 $z$ 를 사용하여 새로운 데이터를 생성할 수 있습니다.

Q2: 훈련 시 $q(z|x)$ 에서 가장 확률이 높은 $z$ 하나만 샘플링해야 하나요?
A2: 아닙니다. 목적 함수가 기댓값(expectation) 형태이므로 분포에 따라 샘플링해야 합니다. 가장 가능성 높은 값만 선택하는 것은 전체 분포를 커버하지 못하게 합니다. 더 정확한 추정을 위해 여러 번 샘플링(Monte Carlo)하는 것이 좋지만 비용 문제로 보통 한 번만 수행합니다.

Q3: 플로우 모델에서 $z$ 와 $x$ 의 차원이 같아야 한다면, 이산적인(discrete) 이미지 데이터는 어떻게 처리하나요?
A3: 플로우 모델의 수학적 이론(미분, 자코비안 등)은 연속 공간을 가정합니다. 이미지 픽셀 값은 이산적이지만, 훈련 데이터에 노이즈를 더해 연속적인 것처럼 취급하거나(dequantization), 이산 공간에서의 변환(순열 등)을 연구하는 확장이 존재합니다.

Q4: 플로우 모델은 어떤 도메인에서 VAE보다 유리한가요?
A4: 플로우 모델은 데이터의 우도(Likelihood)를 정확하게 계산할 수 있다는 장점이 있습니다. 최근 확산 모델(Diffusion Models)도 일종의 아주 깊은 플로우 모델로 해석할 수 있으며, 우도 평가가 필요한 경우 플로우 관점에서 접근하는 것이 유용합니다.

핵심 내용

VAE의 이중적 해석: VAE는 입력 재구성을 위한 오토인코더 손실과 잠재 변수를 사전 분포와 일치시키기 위한 KL 발산 정규화의 결합으로 이해할 수 있습니다. 이를 통해 결정론적 압축이 아닌 확률적 생성 모델로 작동합니다.
노말라이징 플로우의 정의: 간단한 분포를 역변환 가능한(Invertible) 함수들의 합성을 통해 복잡한 데이터 분포로 변환하는 생성 모델입니다. VAE와 달리 잠재 변수의 차원이 데이터와 동일하며, 우도를 정확히 계산할 수 있습니다.
변수 변환 공식의 중요성: 플로우 모델의 학습은 변수 변환(Change of Variables) 공식에 기반합니다. 변환된 변수의 확률 밀도를 구할 때 함수 역변환의 자코비안 행렬식(Determinant of Jacobian)을 통해 부피 변화를 보정해 주어야 합니다.