[CV] CS236 8강 정리 [Normalizing Flows]

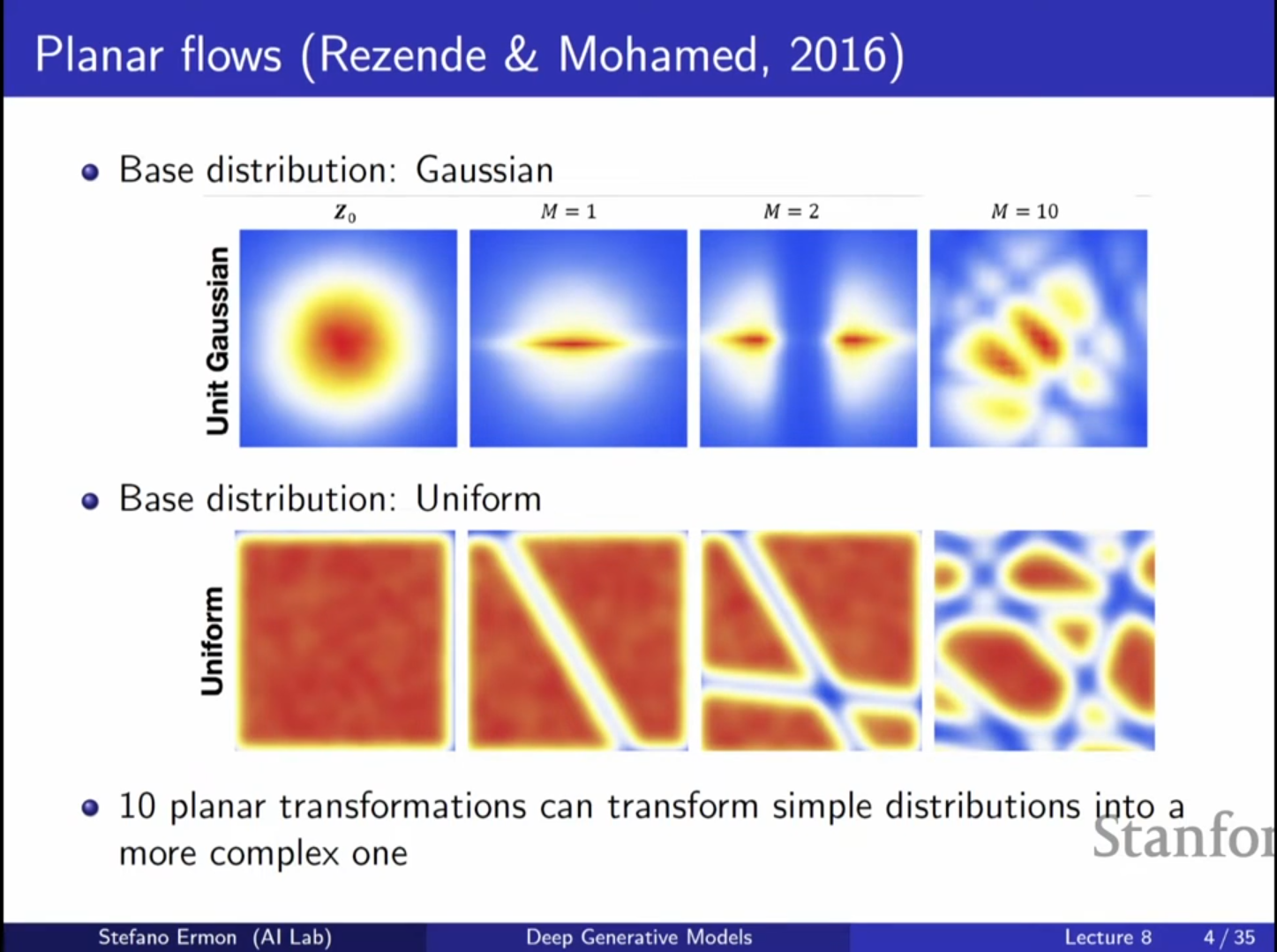
1. Normalizing Flow의 핵심 개념 복습 및 확장

기본 원리

• Normalizing Flow 모델은 잠재 변수(Latent Variable) 모델의 일종으로, 가변 추론(Variational Inference)에 의존하지 않고 정확한 우도(Exact Likelihood)를 계산할 수 있다는 장점이 있습니다.
• VAE(Variational Autoencoder)와 달리, 관측 변수 $x$와 잠재 변수 $z$ 사이의 관계가 결정론적(Deterministic)이고 가역적(Invertible)입니다.
• 따라서 $x$를 얻기 위해 $z$에 변환 함수 $f_\theta$를 적용하며, 반대로 $z$를 추론하려면 역함수를 계산하면 됩니다.

변수 변환 공식 (Change of Variable Formula)

• 데이터 $x$의 확률 $p_x(x)$를 계산하기 위해, $x$를 $z$로 역변환한 후 사전 분포(Prior) $p_z(z)$에서의 확률을 평가하고, 야코비안(Jacobian)의 행렬식(Determinant)을 통해 보정합니다.
• 수식은 다음과 같습니다:
  $\log p_x(x) = \log p_z(z) + \log \left| \det \left( \frac{\partial f^{-1}(x)}{\partial x} \right) \right|$
• 여기서 야코비안의 행렬식은 변환 과정에서 공간의 부피가 국소적으로 얼마나 확대되거나 축소되는지를 나타냅니다.

심화 내용: 차원의 제약

• Normalizing Flow의 중요한 제약 사항은 $x$와 $z$가 동일한 차원을 가져야 한다는 점입니다.
• 이는 $z$가 데이터의 압축된 표현(Compact Representation)을 학습할 수 있는 VAE와 대비되는 점으로, 가역성을 보장하기 위한 필수 조건입니다.

---

2. Deep Normalizing Flow의 구성

흐름(Flow)의 구성

• 복잡한 분포를 모델링하기 위해 딥러닝의 계층적 접근 방식을 사용합니다. 즉, 단순한 가역 함수들을 여러 번 합성하여 복잡한 변환 함수 $f_\theta$를 구성합니다.
• $z_0$에서 시작하여 $f_1, f_2, ..., f_M$을 거쳐 최종 샘플 $x$를 생성합니다.
  $x = f_M(f_{M-1}(...f_1(z_0)...))$
• 각 개별 층(Layer)이 가역적이라면, 이들의 합성은 자동으로 가역적입니다.

야코비안 행렬식의 연쇄 법칙

• 전체 변환의 야코비안 행렬식은 각 개별 변환의 야코비안 행렬식의 곱과 같습니다.
• 따라서 로그 공간에서는 각 층의 로그 행렬식의 합으로 표현되므로 계산이 용이해집니다.

---

3. 효율적인 연산을 위한 구조적 제약

계산 복잡도 문제

• 일반적인 $N \times N$ 행렬의 행렬식(Determinant)을 계산하는 데는 $O(N^3)$의 비용이 듭니다. 데이터 차원 $N$이 클 경우(예: 이미지 픽셀 수), 이는 매우 비효율적입니다.

삼각 행렬(Triangular Matrix) 전략

• 이 문제를 해결하기 위해 야코비안 행렬이 삼각 행렬(Triangular Matrix) 형태가 되도록 변환 함수를 설계합니다.
• 삼각 행렬의 행렬식은 대각 성분(Diagonal entries)의 곱만으로 간단히 계산할 수 있어 연산 비용을 $O(N)$으로 줄일 수 있습니다.
• 이를 위해 변수들 간의 순서(Ordering)를 정하고, $i$번째 출력이 이전 입력들 $x_{1:i-1}$에만 의존하도록 하는 자기회귀(Autoregressive) 구조를 활용합니다.

---

4. 주요 아키텍처: NICE와 RealNVP

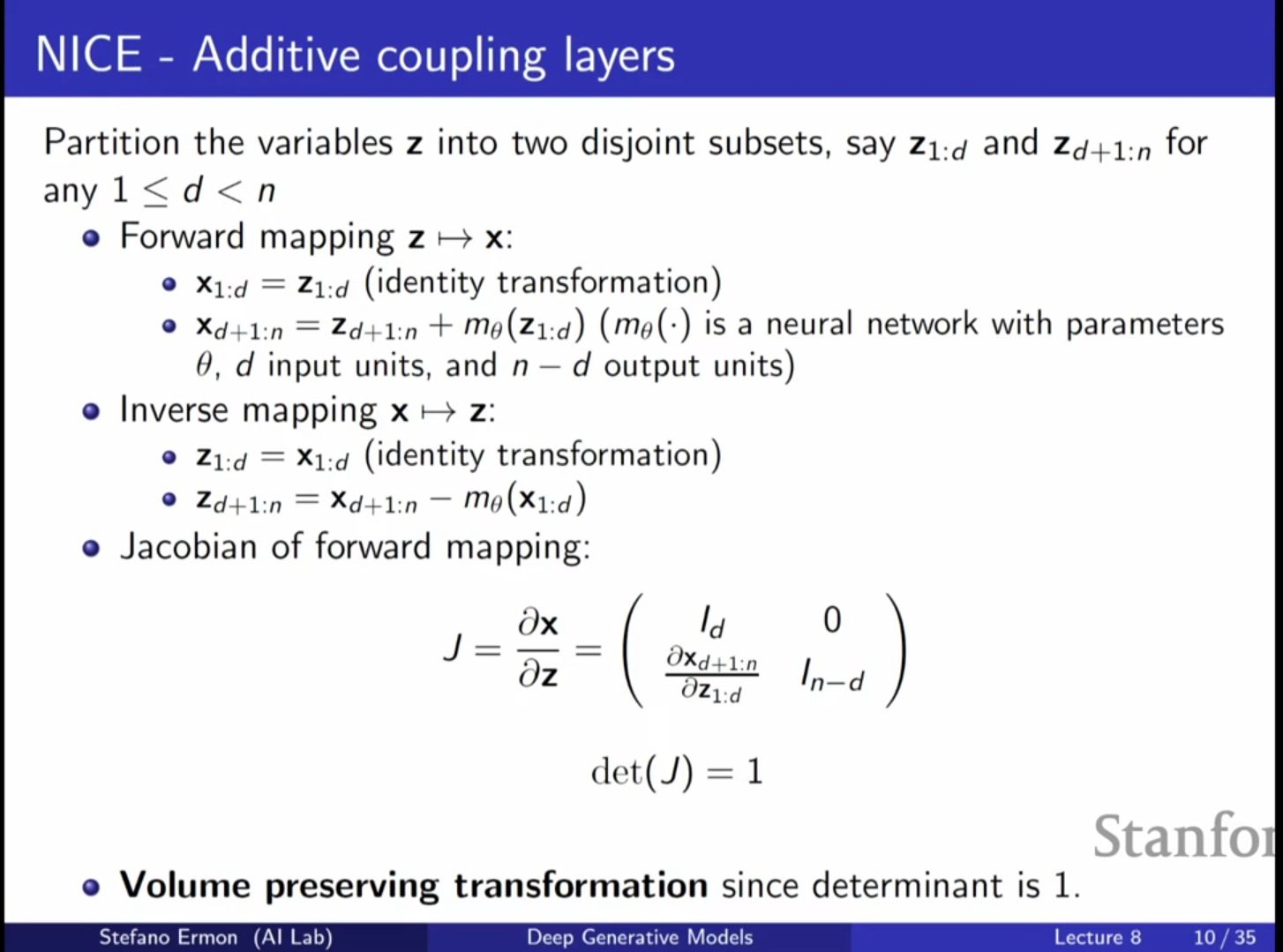
NICE (Non-linear Independent Components Estimation)

• 가장 간단한 형태의 Flow 모델로, Additive Coupling Layer를 사용합니다.
• 작동 원리:
  1. 변수 $z$를 두 그룹 $z_{1:d}$와 $z_{d+1:n}$으로 나눕니다.
  2. 첫 번째 그룹은 그대로 통과시킵니다: $x_{1:d} = z_{1:d}$.
  3. 두 번째 그룹은 첫 번째 그룹을 입력으로 하는 신경망 $m_\theta$의 출력을 더해서 이동(Shift)시킵니다: $x_{d+1:n} = z_{d+1:n} + m_\theta(z_{1:d})$.
• 역변환: 덧셈의 역연산인 뺄셈을 통해 쉽게 역변환이 가능합니다.
• 특징: 야코비안이 대각 성분이 모두 1인 삼각 행렬이 됩니다. 따라서 행렬식은 항상 1이며, 이를 부피 보존(Volume Preserving) 변환이라고 합니다.
• 한계 및 보완: 마지막 층에 간단한 스케일링(Rescaling) 레이어를 추가하여 표현력을 높입니다.

RealNVP (Real Non-Volume Preserving)

• NICE를 확장하여 이동(Shift)뿐만 아니라 스케일링(Scale)까지 수행하는 모델입니다.
• 작동 원리:
  1. 첫 번째 그룹은 그대로 통과시킵니다.
  2. 두 번째 그룹에 대해 신경망으로 계산된 이동 값 $\mu_\theta$와 스케일 값 $\alpha_\theta$를 적용합니다.
     $x_{d+1:n} = z_{d+1:n} \cdot \exp(\alpha_\theta(z_{1:d})) + \mu_\theta(z_{1:d})$
• 역변환: 역연산(뺄셈 및 나눗셈)을 통해 쉽게 계산 가능합니다.
• 특징: 야코비안 행렬식이 1이 아니며, 스케일링 팩터들의 곱으로 결정됩니다. 이는 데이터의 부피를 국소적으로 축소하거나 확대할 수 있어 더 유연한 분포 모델링이 가능합니다.

---

5. 자기회귀 흐름 (Autoregressive Flows)

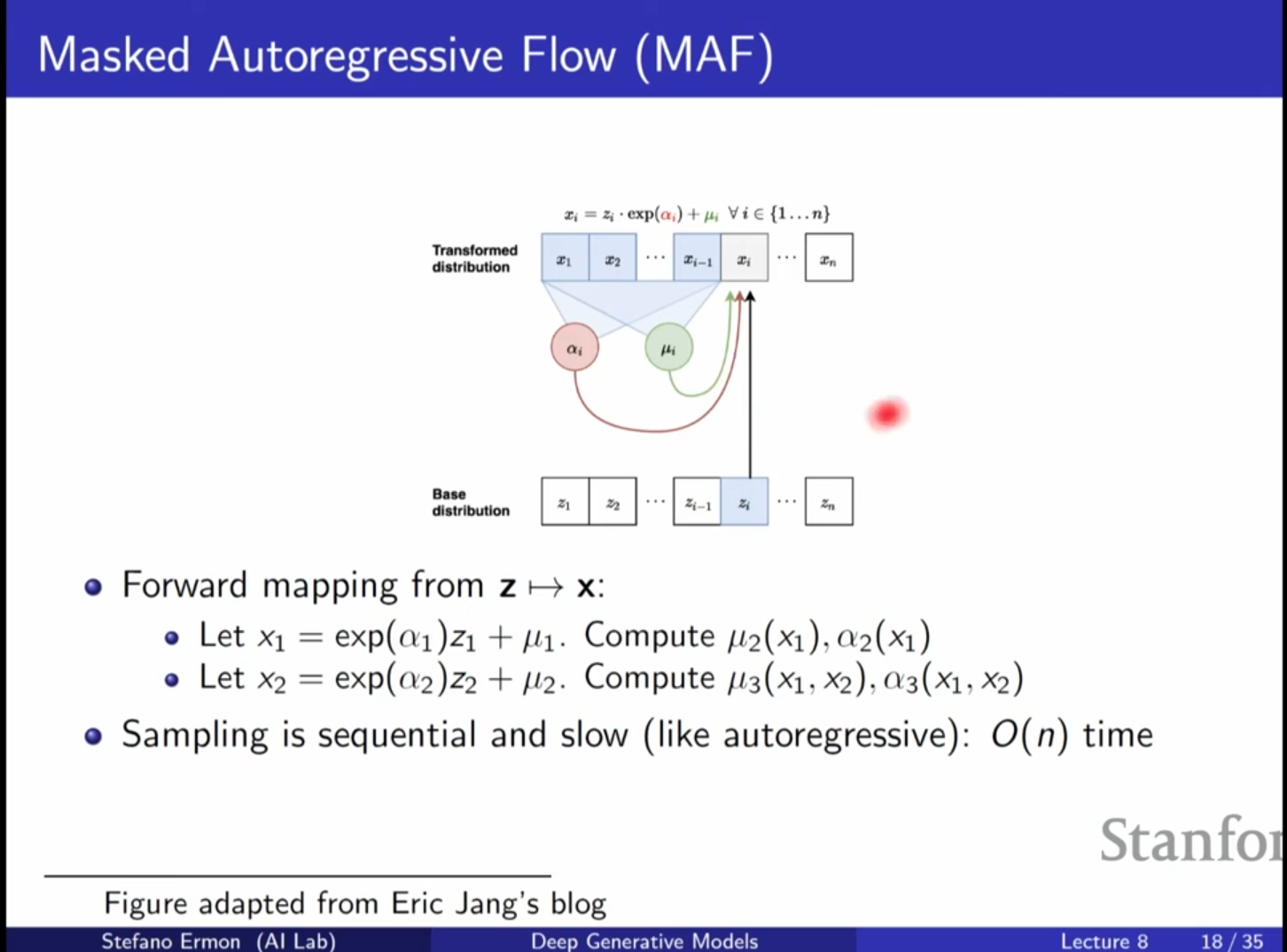
MAF (Masked Autoregressive Flow)

• 연속형 자기회귀(Autoregressive) 모델을 Normalizing Flow로 해석한 것입니다.
• 구조: 각 변수 $x_i$는 이전 변수들 $x_{1:i-1}$에 의존하는 가우시안 분포의 평균과 분산으로 모델링됩니다. 이를 $z_i$를 이동 및 스케일링하는 과정으로 볼 수 있습니다.
• 장점 (학습 시): 데이터 $x$가 주어졌을 때 $z$를 계산(역변환)하는 과정과 우도 계산을 병렬로 수행할 수 있어 학습 속도가 빠릅니다.
• 단점 (샘플링 시): $z$에서 $x$를 생성(순방향)할 때는 순차적으로 계산해야 하므로 샘플링 속도가 느립니다.

IAF (Inverse Autoregressive Flow)

• MAF의 입력과 출력을 뒤집은 형태의 모델입니다.
• 장점 (샘플링 시): $z$에서 $x$를 생성하는 과정이 병렬화되어 샘플링 속도가 매우 빠릅니다.
• 단점 (학습 시): 데이터 $x$의 우도를 계산하기 위해 $z$를 역추적하는 과정이 순차적이므로, 학습(MLE) 속도가 느립니다.

심화 내용: MAF와 IAF의 이중성(Duality)

• MAF와 IAF는 본질적으로 $x$와 $z$의 역할을 서로 바꾼 동일한 구조의 모델입니다. 어떤 방향을 병렬화할 수 있느냐에 따라 이름과 용도가 달라집니다.
• MAF는 학습(밀도 추정)에 유리하고, IAF는 추론(생성)에 유리합니다.

---

6. 지식 증류 (Knowledge Distillation): Parallel WaveNet

문제 상황

• 고품질의 음성 생성을 위해 WaveNet(자기회귀 모델, 즉 MAF 형태)을 사용하면 성능은 좋지만 샘플링 속도가 너무 느려 실제 서비스에 적용하기 어렵습니다.

해결책: Teacher-Student 학습

• Teacher 모델: 학습이 효율적인 MAF(WaveNet) 구조로 먼저 고성능 모델을 학습시킵니다.
• Student 모델: 샘플링이 효율적인 IAF 구조를 사용합니다.
• 증류(Distillation): Teacher 모델의 지식을 Student 모델로 전이합니다. 이때 손실 함수로 KL Divergence를 사용합니다.
  $D_{KL}(P_{Student} || P_{Teacher})$
• 핵심 트릭: Student 모델(IAF)은 자신의 샘플을 빠르게 생성할 수 있고, 생성된 샘플에 대한 확률 밀도도 빠르게 계산할 수 있습니다(자가 생성 샘플에 대해서는 $z$를 이미 알고 있으므로). Teacher 모델(MAF)은 주어진 샘플에 대한 확률 밀도를 빠르게 평가할 수 있습니다. 이 조합을 통해 효율적인 학습이 가능합니다.

---

7. 기타 Flow 아키텍처

Convolutional Flows

• 이미지 데이터의 공간적 특성을 살리기 위해 합성곱(Convolution) 연산을 사용합니다.
• 가역성을 보장하고 야코비안 계산을 쉽게 하기 위해 마스킹된 합성곱(Masked Convolution)을 사용하여 자기회귀적 구조를 강제합니다.

Gaussianization Flows

• 데이터의 분포를 가우시안으로 변환(Gaussianization)하는 관점에서 접근합니다.
• 데이터의 CDF(누적 분포 함수)를 이용해 균등 분포(Uniform)로 변환하고, 다시 가우시안의 역 CDF를 적용하여 가우시안 분포로 매핑하는 방식을 층마다 반복 적용합니다.

---

강의 Q&A

Q1: 신경망 $f_\theta$를 하나의 거대한 네트워크로 한 번에 표현하지 않고 여러 층으로 나누는 이유는 무엇입니까?

• A1: 이론적으로는 하나의 복잡한 함수로 표현 가능하지만, 딥러닝의 철학은 단순한 블록들을 쌓아서 유연성을 얻는 것입니다. 단순한 층(예: 선형 변환 + 비선형성)을 깊게 쌓음으로써, 개별 층은 역변환과 야코비안 계산이 쉬우면서도 전체적으로는 매우 복잡한 변환을 모델링할 수 있습니다.

Q2: Flow 모델의 잠재 변수 $z$는 VAE처럼 의미 있는 구조를 가집니까?

• A2: Flow 모델은 압축을 수행하지 않으므로(차원 동일) VAE만큼 컴팩트하지는 않을 수 있습니다. 하지만 학습된 모델의 잠재 공간에서 보간(Interpolation)을 수행해 보면, 이미지 간의 부드러운 전환이 일어나는 등 의미 있는 구조를 학습했음을 확인할 수 있습니다.

Q3: 언어 모델(텍스트)에도 이 방식을 적용할 수 있습니까?

• A3: 어렵습니다. Normalizing Flow는 연속 확률 변수에 대한 변수 변환 공식을 기반으로 하므로, 이산적인(Discrete) 텍스트 데이터에는 직접 적용할 수 없습니다. 이산 데이터를 연속 분포로 변환하는 과정이 미분 불가능하거나 가역적이지 않기 때문입니다.

---

## 핵심 내용

1. 가역성과 정확한 우도: Normalizing Flow는 결정론적이고 가역적인 변환을 통해 단순한 분포(가우시안)를 복잡한 데이터 분포로 매핑하며, 변수 변환 공식을 통해 정확한 우도(Exact Likelihood) 계산이 가능합니다.
2. 효율적인 구조 설계: 계산 비용이 높은 야코비안 행렬식 계산을 $O(N)$으로 줄이기 위해, 삼각 행렬 야코비안을 생성하는 구조(Coupling Layer, Autoregressive structure)를 사용하여 모델을 설계합니다 (예: NICE, RealNVP).
3. MAF와 IAF의 트레이드오프: 자기회귀 기반 Flow 모델에서 MAF는 학습(우도 계산)이 빠르고, IAF는 생성(샘플링)이 빠릅니다. Parallel WaveNet은 이 두 모델의 장점을 결합하여 지식 증류를 통해 고속 고품질 생성을 달성했습니다.