LassoNet: Neural Networks with Feature Sparsity

이번 논문은 2020년 스탠포드에서 쓴 XAI 관련 연구이다. 이 연구의 후속 연구인 FastCPH model 이 얼마전 1월에 나와서 읽는 중에 이 논문은 리뷰하면 재밌을 것 같았다. 지금까지 해석 가능한 AI 와 관련된 많은 연구가 이루어졌고, 하나의 접근 방식은, 네트워크가 중요한 feature 만 사용하도록 arrange 하는 것이다. 주로 Linear model 에서 Lasso (l1-penalty) regularization 은 가장 관련없는 feature 에 0 을 부여하는 방향으로 학습이 이루어지도록 하지만, linear model 에만 적용 가능했다. 이번 논문에서는 nonlinearity 를 머금고 있는 neural network 에 feature sparsity 를 수행하도록 강제하는 새로운 학습 방법 및 알고리즘을 제안한다. 해당 논문의 요약은 다음 영상에서 확인할 수 있다. https://www.youtube.com/watch?v=bbqpUfxA_OA

Introduction

• 예측 문제에서 much of information in features is irrelevant
• high dimensional data - speech, object recognition, protein data
• benefits of feature selection include, 1) reduce experimental cost, 2) enhance interpretability 3) speed up 4) memory
• motivating question: Are there redundant or unnecessary features?

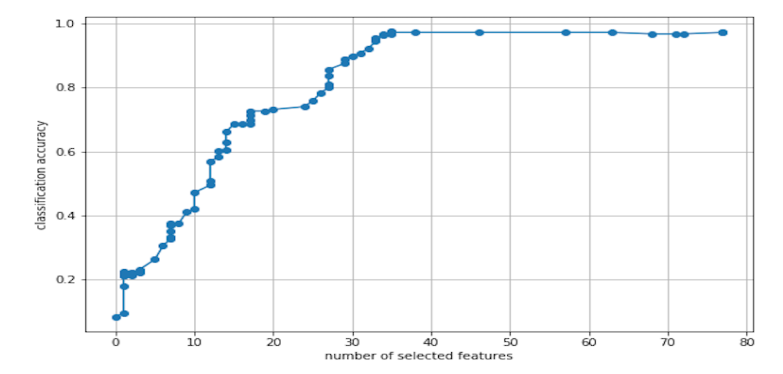
MICE protein dataset 에서 20%의 feature 만으로 70%의 signal 을 잡아냄. 절반 이하 35개의 feature 만으로 좋은 성능.

Proposed method

new approach LassoNet
: extends Lasso regression and its feature sparsity - to FeedForwardNeuralNetworks.
: input-to-output residual connection 을 활용하여, allow a feature to have non-zero weight in a hidden unit only if its linear connection is active
: linear-nonlinear components are optimized jointly, allowing to capture arbitrary nonlinearity
: outperforms state-of-the-art methods for feature selection and regression

Our proposal: LassoNet

Background and notation

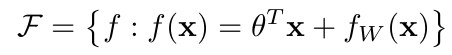
n: total number of training points
d: data dimension
$f_W$: fully connected feed-forward network with parameters W
K: the size of the first hidden lyaer
$W^{(1)}$: first hidden layer (dxK-dimensional)
$\theta$: residual layer (d-dimensional)
$S_{\lambda}(x)$: sign(x)max(|x|-$\lambda$, 0), soft thresholding operator

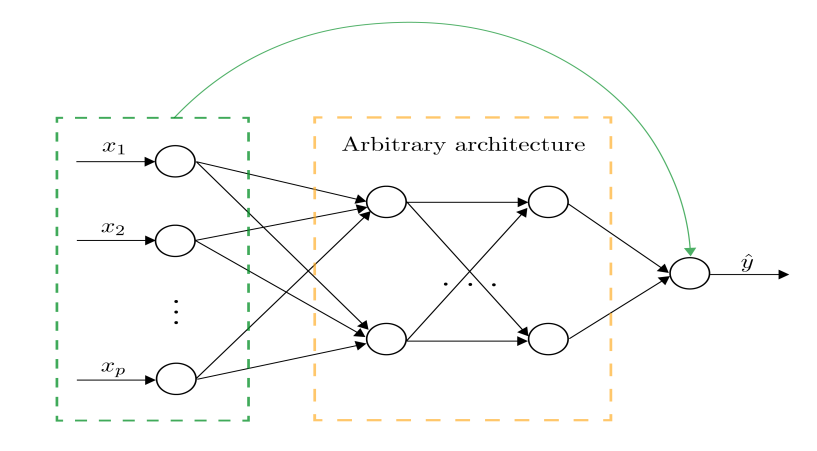
green: single residual connection, black: arbitrary feed-forward neural network.
The residual layer and the first hidden layer are jointly passed through a hierarchical soft-thresholding optimizer

1) penalty 는 기존 feature sparsity 로 이끄는 empirical risk minimization 을 따른다. combinatorial search 에서 continuous search by varying the level of the penalty.
2) proximal gradient algorithm 은 수학적으로 elegant way 로 적용되어, simple - efficient 적용이 가능하다.

Formulation

이 논문에서 가장 핵심이라 말할 수 있는 부분이 다음 식이다.

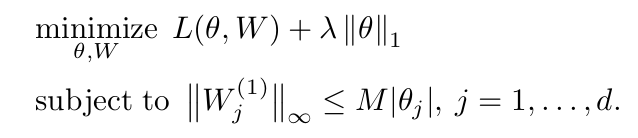
특히 아래 constraint 부분이 포인트라고 할 수 있다. M 이라는 constant 에 따라, non-linearity involving feature j according to the relative effect importnace of $X_j$ 의 양이 조절된다. 즉, M=0 일 때 formulation 은 linear model 에서의 LASSO 와 같아진다. 반대로 M->inf 로 가면 standard feed-forward network with $l_1$-penalty on first layer 가 된다.

이 formulation 은 몇가지 장점이 있는데, (의역 불가) linear component of the signal above the nonlinear one and 이를 feature sparsity로 이끈다. (이는 hierarchy priciple 이라는 통계학의 개념과 유사하다고 한다. 완전히 새로운 것은 아니라 함) 또한, linear and non-linear component 를 학습 과정 상 "simultaneously" 배우게 된다.

위 알고리즘은 LassoNet 의 training 과정이다. 먼저 모델 파라미터는 stochastic gradient descent 로 업데이트 된다. 이후 hierarchical proximal operator - optimization section 에 등장 - 가 input layer pair $(\theta, W^{(1)})$ 에 적용된다. elegant 하다는 표현이 참 적합하다 느껴졌다. 하지만 뒤에 무시무시한 증명 과정이 기다리고 있다.

Hyper-parameter

LassoNet 에는 두 가지 hyper-parameter 가 존재한다.

• the $l_1$-penalty coefficient $\lambda$ : controls complexity of the fitted model.
• the hierarchy coefficient $M$: controls the relative strength of the linear and nonlinear components

특히 hierarchy coefficient 는 domain knowledge 없이 설정하는 것이 어렵다고 한다. 미리 정해둔 hyperparameter set 에서 parallel 하게 tuning 했다고 한다.

Optimization

Warm starts: a path from dense to sparse

feature selection 과정을 생각해보면 forward selection, reverse selection 이 있다. 저자는 전자와 후자를 각각 실험했고, 다음과 같은 결과를 얻었다.

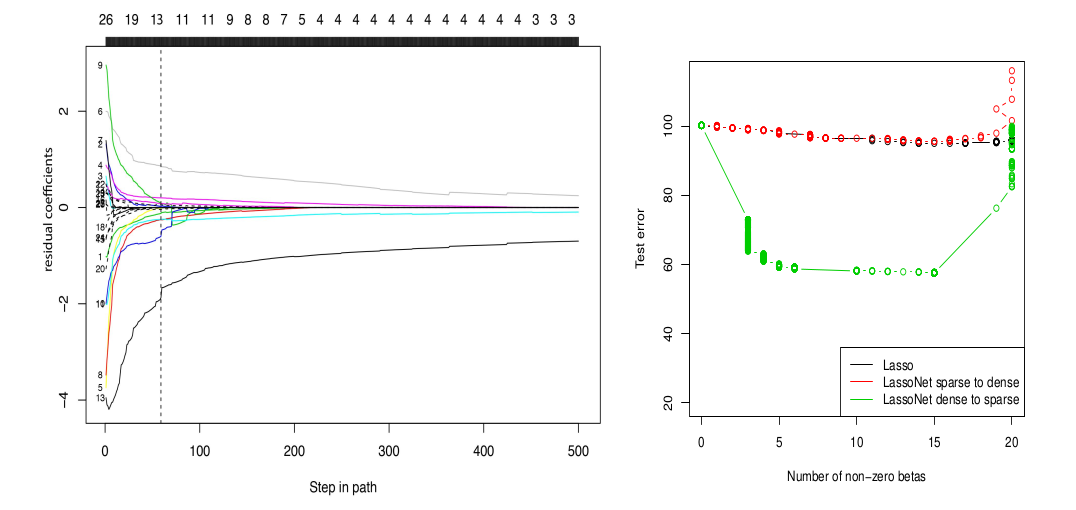
오른쪽 figure 를 보면, Lasso 와 LassoNet sparse to dense (red) 에 비해, LassoNet dense to sparse (green) 의 Test error 가 월등히 낮은 것을 확인할 수 있다.

Hierarchical proximal optimization

위 알고리즘에 등장했던 HIER-PROX() 라는 operator 에 대한 내용이다. 앞서도 간단히 설명했지만, 이는 numerically efficient "algorithm" 이다. (not DL model) 미리 그 존재와 유일성이 증명된 global minima 식을 통해 각 node 의 weight 들을 최적화 하는 과정이다. 필자는 다음과 같이 설명한다. Underlying its development is the derivation of equivalent optimality conditions that completely characterize the global solution of the no-convex minimization porblem defining the proximal operator.

해당 식에서 주목할 점은, inner loop 에서 각 input feature 마다 따로 계산이 가능하다는 점이다. 또한 ranking 을 정해서 하나의 m 을 잡고 이를 이용해서 update 한다는 점이다. 이것이 가능한 이유는 다음 proposition 이 증명되었기 때문이다.

증명과정을 간단히 요약하면, non-convex optimization problem - (KKT condition, strong duality) 을 두 가지 subproblem 으로 나눈다. 이 두 subproblem 은 각각 stochastic gradient descent 와 analytic한 관점에서 iterative 하게 문제를 해결한다.

Experiments

다음 데이터셋을 이용해 실험한다.

• ISOLET (617 dimension): speech data of people speaking the names of letter (alphabet)

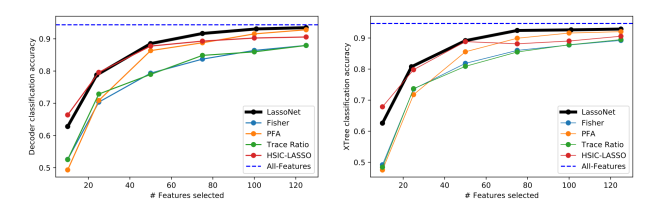
LassoNet 으로 유의마한 feature extraction 을 수행한 뒤, decoder classification acc 와 XTree classification acc 를 관찰하였다.

Application to Unsupervised Feature Selection

MNIST 데이터셋을 이용한 feature extraction 성능을 확인하기 위해, decoder 로 이미지를 복원했다.
특히, GROUP-LASSO 알고리즘을 사용하여, 모든 같은 set 의 selected feature 가 all reconstructed input 에 동일하게 적용되도록 하였다.

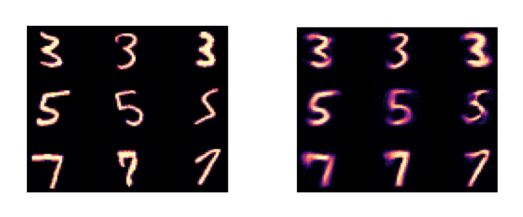
왼쪽은 test images, 오른쪽은 LassoNet 으로 복원한 결과이다.

Application to Matrix Completion

몇몇 biomedical data 등의 데이터는 종종 measurement 자체의 cost 가 높거나 데이터 수집 날짜 등의 다양한 요인에 의해 데이터 소실 문제에 부딪힌다. 즉 missing row 가 많은 편이다. 이를 해결하기 위해 matrix completion problem 이 연구되어 왔는데, 대표적으로 soft-impute algorithm 은 underlying data 가 low-rank 가정을 요한다. (singular value 이용)

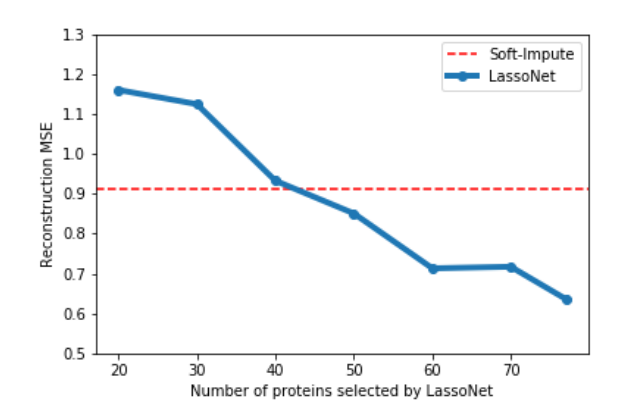
LassoNet 의 결과와 함께 기존 방식의 한계점을 지적한다.
1. low rank assumption 이 항상 모든 데이터에 적합하지 않다.
2. model 의 linear assumption 이 들어맞지 않을 때 성능이 크게 하락한다.

LassoNet 은 iterative 하게 적절한 feature 를 선택하며 feature 개수까지 tuning 가능하고, hyperparameter 를 통해 데이터의 linearity 뿐만 아니라 non-linearity 또한 포함할 수 있기에 성능이 더 잘 나올 수 있었다고 설명한다.