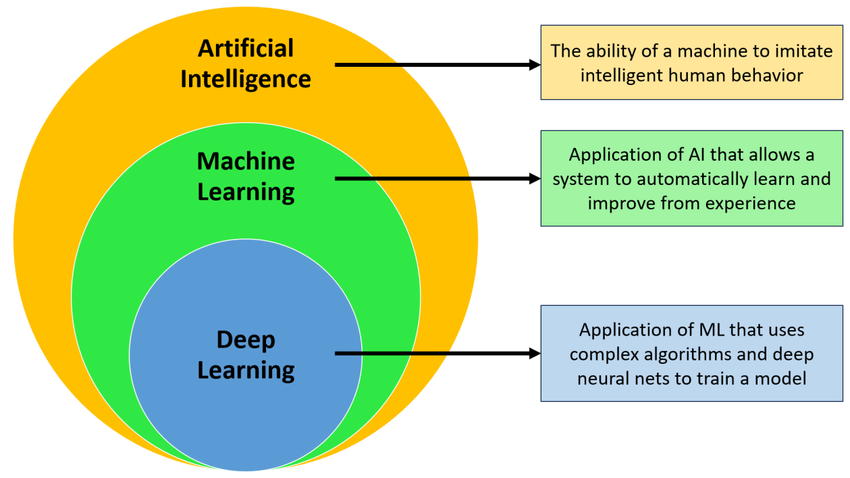
인공지능?
인공지능(AI)은 똑똑한 컴퓨터 또는 지능을 가진 컴퓨터로 이해할 수 있음. 정확한 사전적 정의는 없지만, 대표적인 예로 AI 스피커, Siri 같은 음성 인식, Google이나 Naver Papago와 같은 기계 번역, 자율주행차 등이 있음.
컴퓨터가 지능적인 태스크를 수행하는 방법
컴퓨터가 지능적인 태스크를 수행하는 방식에는 두 가지가 있음:
1. 규칙 기반: 2000년대 초반까지 많이 사용된 방법임. 사람이 문제 해결에 필요한 규칙을 직접 정의해줘야 함. 새로운 문제에 직면할 때마다 규칙을 수정하거나 추가해야 하는 불편함이 있음.
2. 학습 기반: 컴퓨터가 데이터를 학습해서 문제를 해결하는데 필요한 정보를 스스로 추출함. 이를 위해서는 학습 데이터가 필수적임.
기계 학습?
기계 학습은 기계가 학습을 통해 문제를 해결하는 것을 의미함. 여기서 사용되는 것이 기계 학습 알고리즘임. 크게 3가지 유형으로 나뉨:
| 유형 | 설명 | 예시 |
|---|---|---|
| 지도 학습 (Supervised Learning) | 학습 데이터에 정답이 포함되어 있음. 이를 통해 힌트와 정답 간의 관계를 파악하고 새로운 데이터에 적용 | 집값/주식 가격 예측, 스팸 메일 분류 등 |
| 비지도 학습 (Unsupervised Learning) | 정답 없이 데이터 속 패턴을 분석함 | 군집화 분석(옷 추천, 영화 추천 등) |
| 강화 학습 (Reinforcement Learning) | 행동에 따라 보상과 패널티를 받아 더 나은 결과를 유도함 | 컴퓨터 게임 (체스 AI) |
지도 학습의 원리
지도 학습에서 컴퓨터는 학습 데이터를 통해 독립변수(IV)와 종속변수(DV) 간의 관계를 학습함. 그 관계를 바탕으로 새로운 데이터에 대한 예측을 수행함.
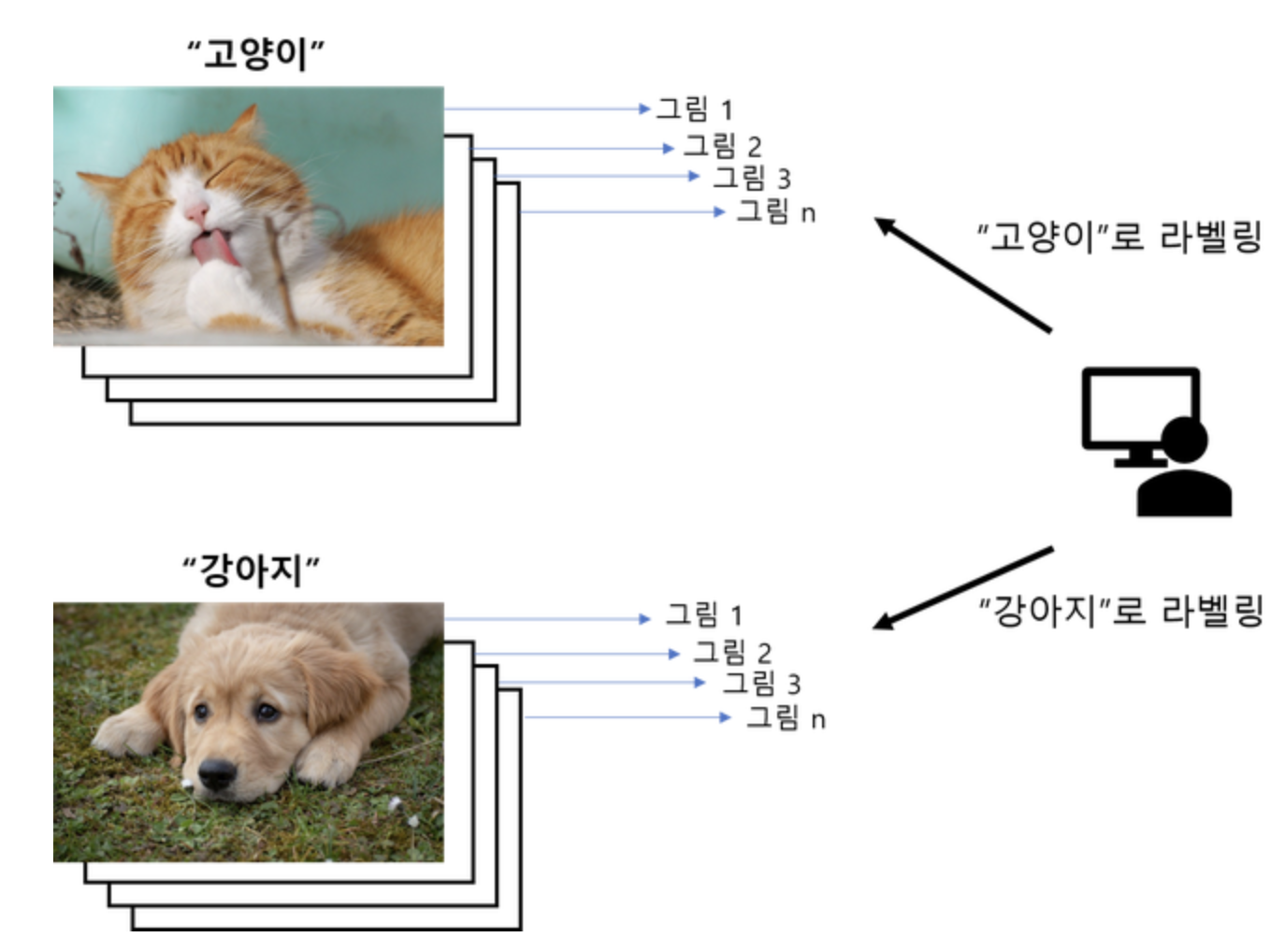
예시 1: 강아지와 고양이 분류
강아지 사진에 "Dogs", 고양이 사진에 "Cats" 라벨을 달아 학습시키면, 컴퓨터는 강아지와 고양이의 차이를 학습하고, 새로운 사진에서 어떤 동물인지 예측할 수 있게 됨.
예시 2: 아파트 가격 예측
아파트 평수를 독립변수로, 아파트 가격을 종속변수로 설정하여 학습 데이터를 기반으로 가격을 예측할 수 있음.
| 관측치 | 평수(IV) | 가격(DV) |
|---|---|---|
| 1 | 30평 | 3억 |
| 2 | 34평 | 4억 |
| 3 | 34평 | 3.8억 |
| 4 | 48평 | 6억 |
1차 함수 모형
기계 학습의 가장 기본적인 수학적 모형은 1차 함수임. y = ax + b로 표현되며, 학습을 통해 데이터에 가장 적합한 파라미터 값을 찾아냄.
지도 학습 모형을 이용한 문제의 종류
지도 학습 모형을 통해 풀 수 있는 문제는 크게 두 가지로 나뉨:
1. 회귀 문제(Regression Problem): 종속변수가 연속변수일 때.
2. 분류 문제(Classification Problem): 종속변수가 이산변수일 때.
문제를 구분할 때는 종속변수의 종류에 따라 회귀 문제인지, 분류 문제인지 구분하게 됨.
변수?
변수는 여러 개의 값 중 하나의 값을 취할 수 있는 것을 의미하며, 영어로는 Variable이라 부름. 대표적인 예로는 나이, 몸무게, 소득, 성별 등이 있음.
변수의 종류
- 연속변수(Continuous Variable): 나이, 몸무게, 소득과 같이 무한한 값 중 하나를 취할 수 있는 변수. 예를 들어, 나이는 정수뿐만 아니라 소수점 단위까지 고려하면 무한한 값 중 하나를 취할 수 있음.
- 이산변수(Discrete Variable): 성별과 같이 유한한 값 중 하나를 취할 수 있는 변수.
이산변수는 두 가지로 분류됨:
1. 명목변수(Nominal Variable): 유한한 값이 특정 그룹의 이름을 의미하는 변수. 예를 들어, 성별은 남성과 여성이라는 두 개의 값을 가질 수 있으며, 이는 각각의 값이 특정 그룹을 의미함.
- 범주형 변수(Categorical Variable): 명목 변수와 유사하게 값이 특정 그룹을 나타냄.
문제 유형에 따른 구분
-
종속변수가 연속변수일 경우: 회귀 문제로 분류됨. 예를 들어, 아파트의 가격 예측 문제는 아파트 가격이 연속변수이므로 회귀 문제에 해당됨.
-
종속변수가 이산변수일 경우: 분류 문제로 분류됨. 예를 들어, 환자가 폐암에 걸렸는지 여부를 예측하는 문제는 이산변수인 0(안 걸림)과 1(걸림)의 값을 가짐. 이 경우, 폐암 여부는 명목변수로서 분류 문제로 간주됨.
| 문제 유형 | 설명 | 예시 알고리즘 |
|---|---|---|
| 회귀 문제 | 종속변수가 연속변수인 문제 | Linear Regression, Feedforward Neural Network |
| 분류 문제 | 종속변수가 이산변수인 문제 | Logistic Regression, SVM, Decision Tree, CNN |
확률 문제도 분류 문제
각각의 값이 나올 확률을 예측하는 문제가 아닌, 0과 1을 예측하는 것 역시 분류 문제에 해당됨. 각각의 확률을 먼저 예측한 뒤, 0 혹은 1에 더 높은 확률에 해당하는 값으로 최종 예측을 하게 됨. 따라서 확률 계산 역시 분류 문제에서 많이 사용되는 방식임.
그러나 환자가 폐암에 걸릴 확률 자체를 알고 싶다면, 이는 연속변수로 간주될 수 있어 회귀 문제로 볼 수 있음. 종속변수가 확률 자체인 경우 회귀 문제로 분류되며, 최종적인 문제의 유형은 종속변수에 따라 달라짐.
학습 과정에서의 오차
오차(Error)는 실제 값과 예측 값의 차이를 의미하며, 학습 과정에서 이를 최소화하는 것이 목표임. 각 관측치의 오차는 아래와 같이 정의됨:
| 공식 | 설명 |
|---|---|
| e_i = y_i - y^ | e_i: i번째 관측치의 오차, y_i: 실제 값, y^: 예측 값 |
결국 학습을 통해 파라미터의 최적 값을 찾아 예측 성능을 높이는 것이 기계 학습의 목표임.
