트리

트리(Tree)란?

트리는 노드로 이루어진 자료구조로서 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조입니다.

트리에는 여러 종류가 있어서 해당 종류에 대해 각각 알아보기 전에 먼저 공통적인 특징과 용어에 대해서 설명하고 넘어가겠습니다.

특징

1. 트리는 하나의 루트 노드를 갖는다.
   => 루트 노드는 0개 이상의 자식 노드를 갖고 있다.
   => 그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.
   => 임의의 두 노드간의 경로는 유일하다.
   => 노드 N개인 트리는 항상 N-1개의 간선(Edge)을 가진다. (즉, 간선의 수 = 정점의 개수 - 1)

2. 노드(node)들과 노드들을 연결하는 간선(edge)들로 구성되어 있다.
   => 트리에는 사이클(cycle)이 존재할 수 없다.
   => 노드들은 특정 순서로 나열될 수 있고 그럴 수 없을 수도 있다.
   => 각 노드는 부모 노드로의 연결이 있을 수도 있고 없을 수도 있다.
   => 각 노드는 어떤 자료형으로도 표현 가능하다.

3. 비선형 자료구조로 계층적 관계를 표현한다.
   Ex) 디렉터리 구조, 조직도

4. 그래프의 한 종류이다. ‘최소 연결 트리’라도도 불린다.
   => 사이클(cycle)이 없는 하나의 연결 그래프(Connected Graph)
   => 또는 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한 종류 이다.

용어

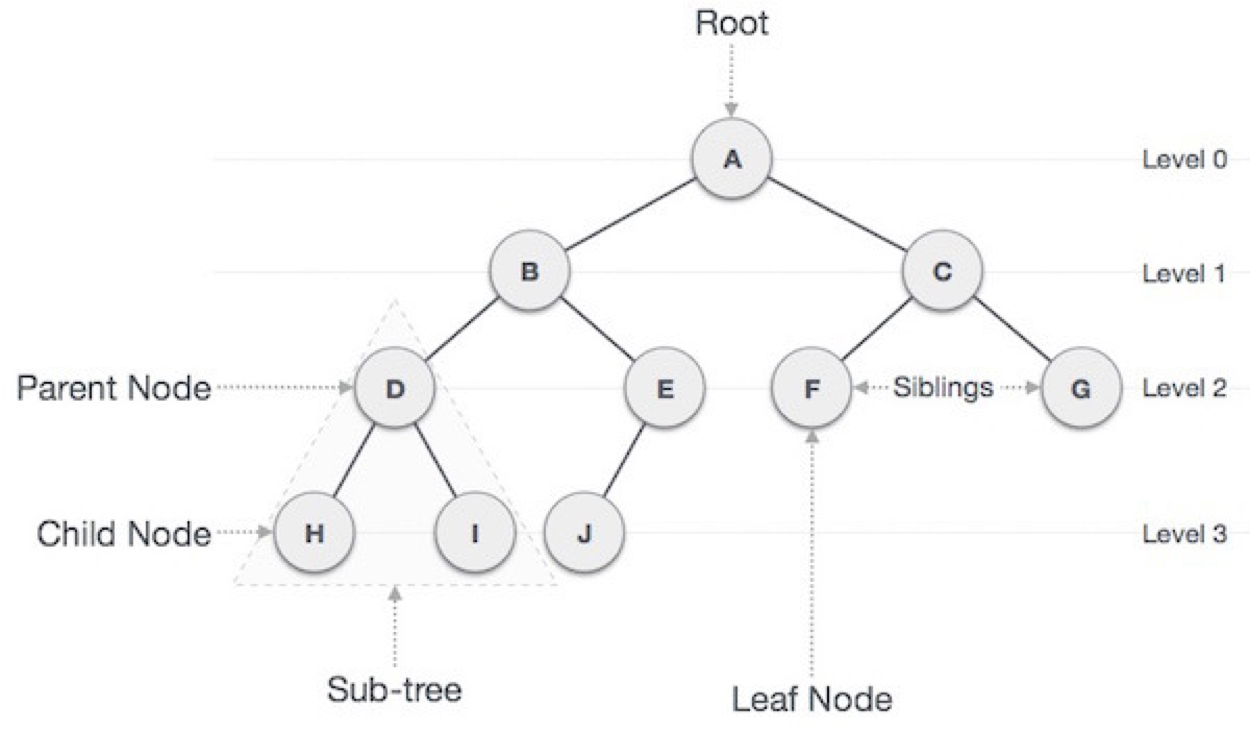
• 루트 노드(Root Node): 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
• 단말 노드(Leaf Node): 자식이 없는 노드, ‘말단 노드’ 또는 ‘리프 노드’라고도 부른다.
• 내부 노드(Internal Node): 단말 노드가 아닌 노드
• 간선(Edge): 노드를 연결하는 선 (Link, Branch라도도 부른다.)
• 형제(Sibling): 같은 부모를 가지는 노드
• 노드의 크기(Size): 자신을 포함한 모든 자손 노드의 개수
• 노드의 깊이(Depth): 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
• 노드의 차수(Degree): 하위 트리 개수 / 간선 수 = 간 노드가 지닌 가지의 수
• 트리의 차수(Degree of Tree): 트리의 최대 차수
• 트리의 높이(Height): 루트 노드에서 가장 깊숙히 있는 노드의 깊이

종류(알고리즘)

1. 이진 트리 + 이진 탐색 트리
2. 이진 힙(최대 힙, 최소 힙)
3. 세그먼트 트리(Segment Tree)
4. 느리게 갱신되는 세그먼트 트리(Segment Tree with Lazy Propagation)
5. LCA 알고리즘(Lowest Common Ancestor)
6. B-Tree
7. 균형 트리(AVL 트리, Red-Black 트리)

트리에는 여러 종류가 있는 것으로 알고 있고, 계속 학습하는 대로 정리를 할 예정입니다. 또한, 트리에서 사용되는 알고리즘도 정리하도록 하겠습니다.

각각 트리에 대해서는 다른 페이지에서 따로 정리를 해놓았고, 서로의 트리의 특징을 비교하는 것은 해당 페이지에서 정리할 예정입니다. 또한, 공통적인 부분 또한 여기에 정리를 할 예정입니다.

비교

대표적인 트리에 관해서만 비교를 해가며 알기 쉽게 정리해보도록 하겠습니다.

트리 VS 이진 트리

• 이진 트리(Binary Tree)
  • 각 노드가 최대 두 개의자식을 갖는 트리
  • 모든 트리가 이진 트리는 X
  • 이진 트리 순회
    • 중위 순회(In-Order traversal): left → root → right
    • 전위 순회(pre-Order traversal): root →left → right
    • 후위 순회(post-Order traversal): left → right → root

이진 트리 VS 이진 탐색 트리

• 이진 탐색 트리(Binary Search Tree)
  • 모든 노드가 특정 규칙(순서)을 따르는 속성이 있는 이진 트리
  • 모든 왼쪽 자식들 ≤ n ≤ 모든 오른쪽 자식들(모든 노드 n에 대해서 반드시 참)

균형 트리 VS 비균형 트리

• 균형 트리
  • 오른쪽 서브트리의 높이와 왼쪽 서브 트리의 높이 차이가 1 이하인 이진 탐색 트리를 말함.
  • O(logN) 시간에 Insert와 Find를 할 수 있을 정도로 균형이 잘 잡혀 있는 경우
  • Ex) Red-Black Tree, AVL트리

완전 이진 트리 VS 전 이진 트리 VS 포화 이진 트리

• 완전 이진 트리(Complete Binary Tree)

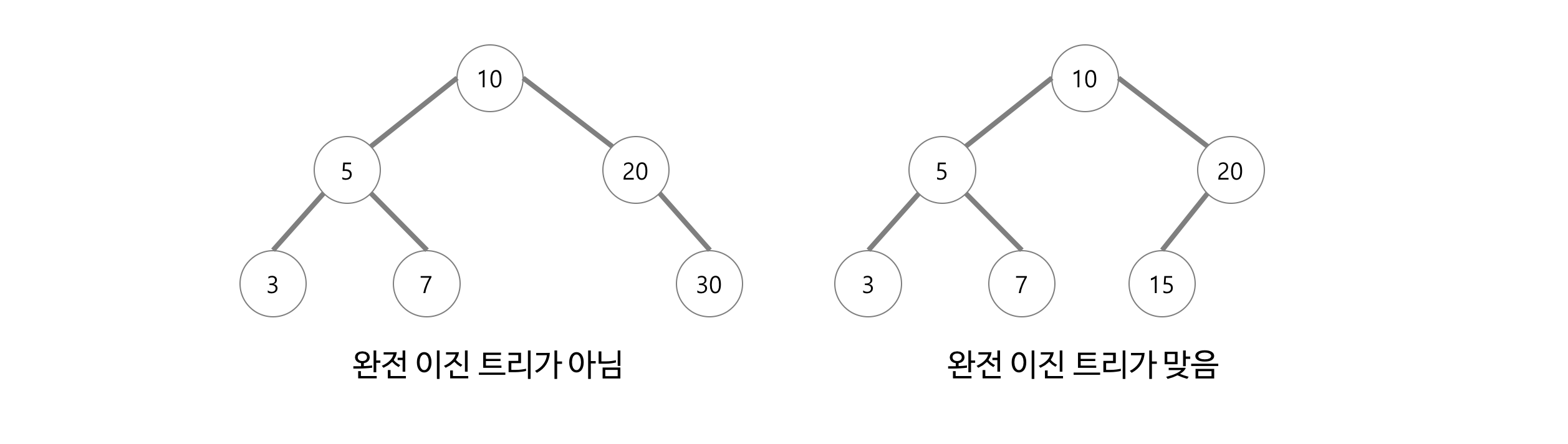
• 트리의 모든 높이에서 노드가 꽉 차 있는 이진 트리. 즉, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
• 마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
• 마지막 레벨 h에서 1 ~ 2(h - 1)개의 노드를 가질 수 있다.
• 완전 이진 트리는 배열을 사용해 효율적으로 표현 가능하다.
• 전 이진 트리(Full Binary Tree 또는 Strictly Binary Tree)

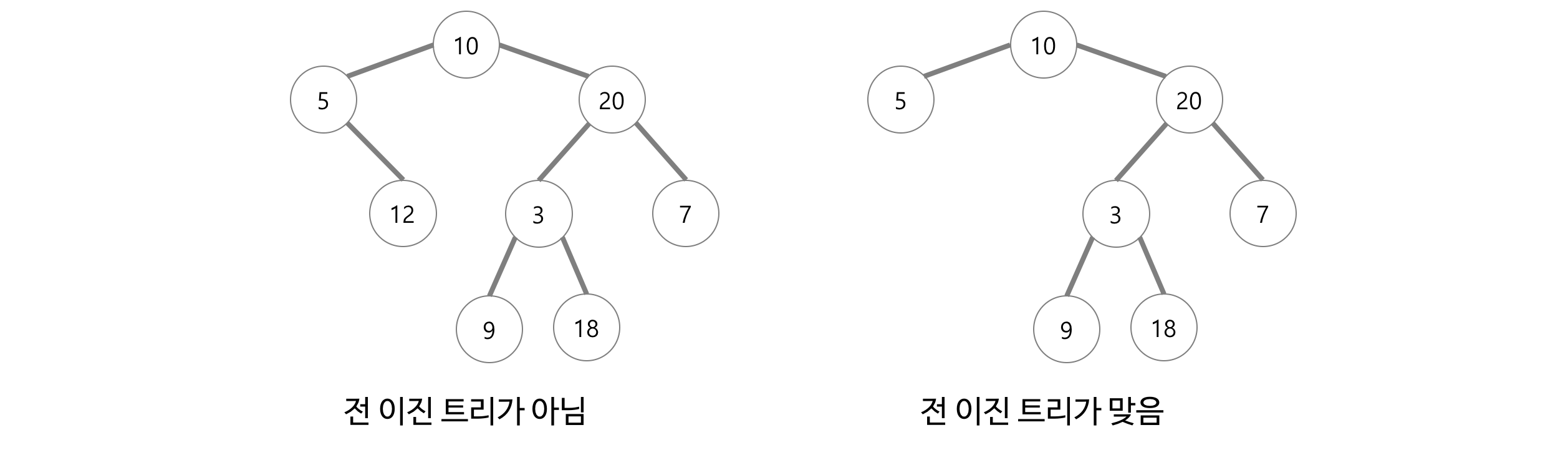
• 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
• 포화 이진 트리(Perfect Binary Tree)

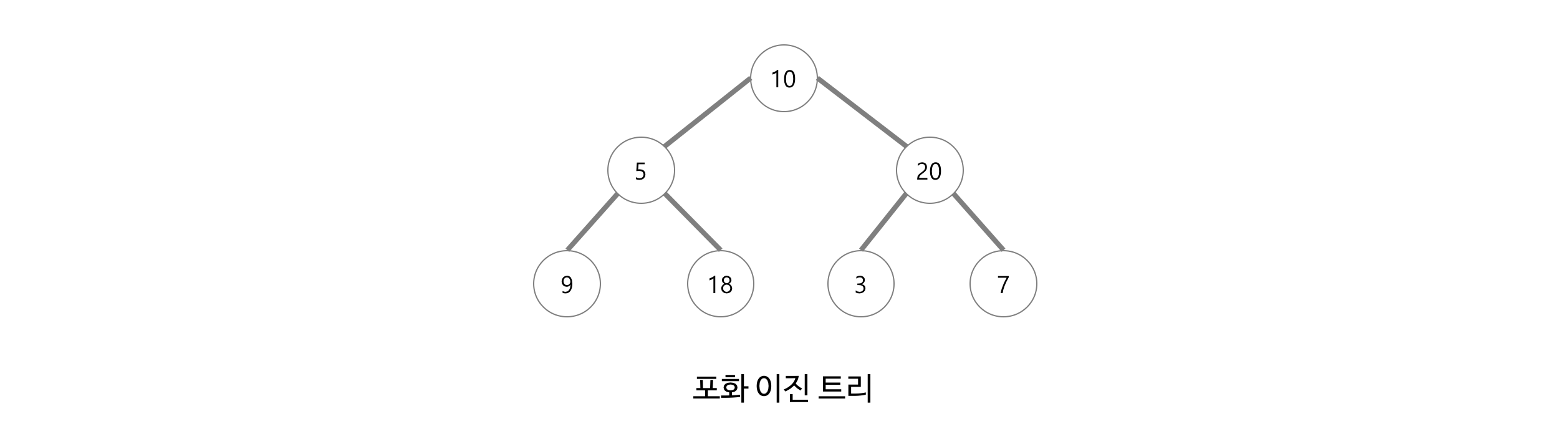
• 전 이진 트리이면서 완전 이진 트리인 경우
• 모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다.
• 모든 내부 노드가 두 개의 자식 노드를 가진다.
• 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다.
• 노드의 개수 = 2(k-1) (k: 트리의 높이)

이진 힙(최소 힙과 최대 힙)

• 최소 힙(Min Heap)
  • 모든 서브 트리에서 루트 노드가 자식 노드보다 작은 값을 가지는 완전 이진 트리를 의미합니다.
    • 가장 작은 값 = Root Node
• 최대 힙(Max Heap)
  • 모든 서브 트리에서 루트 노드가 자식 노드보다 큰 값을 가지는 완전 이진 트리를 의미합니다.
    • 가장 큰 값 = Root Node
• 최소 힙, 최대 힙 두 경우 모두 노드 N개가 힙에 들어가 있으면 높이는 log(N)입니다.

트리(Tree)의 구현 방법

기본적으로 트리는 그래프의 한 종류이므로 그래프의 구현 방법으로 구현 할 수 있습니다.

1. 인접 배열 이용
2. 인접 리스트 이용

인접 배열 이용

1. 1차원 배열에 자신의 부모 노드만 저장하는 방법
   a. 트리는 부모 노드를 0개 또는 1개를 가지기 때문
   b. 부모 노드를 0개: 루트 노드
2. 이진 트리의 경우, 2차원 배열에 자식 노드를 저장하는 방법
   a. 이진 트리는 각 노드가 최대 두개의 자식을 갖는 트리이기 때문
   b. Ex) A[i][0]: Left Child Node, A[i][1]: Right Child Node
   

인접 리스트 이용

1. 가중치가 없는 트리의 경우
   a. ArrayList<ArrayList> list = new ArrayList<>();
2. 가중치가 있는 트리의 경우
   a. class Node {int idx, int cost; //인접 노드 번호, 거리} 정의
   b. ArrayList[] list = new ArrayList[정점의 수 + 1];

마지막으로 그래프와 트리의 차이를 표로 확인해 봅시다.