합성곱 신경망을 사용한 이미지 분류

데이터 준비하기

패션 MNIST 데이터 불러온 후, 스케일링 후 Train, Validation Set으로 분할

from tensorflow import keras
from sklearn.model_selection import train_test_split

(train_input, train_target), (test_input, test_target) =\
keras.datasets.fashion_mnist.load_data()

train_scaled = train_input.reshape(-1, 28, 28, 1) #이미지에는 항상 깊이(채널)이 있어야 한다. 흑백의 이미지는 채널이 없는 2차원이지만, 다른 이미지는 채널이 RGB로 이루어짐.
train_scaled = train_input / 255.0
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)

첫 번째 합성곱-풀링 층 신경망

model = keras.Sequential()

#32개의 kernel, Same Padding, kernel_size = (3, 3)
model.add(keras.layers.Conv2D(32, kernel_size=3, activation='relu', padding='same', input_shape=(28, 28, 1)))

#풀링 층 추가. 전형적인 (2, 2) 크기의 풀링
#Pooling Layer을 통과하면 데이터는 (28, 28, 32)에서 (14, 14, 32)가 된다.
model.add(keras.layers.MaxPooling2D(2))

두 번째 합성곱-풀링 층 신경망

#64개의 kernel, 3종류의 kernel
model.add(keras.layers.Conv2D(64, kernel_size=3, activation='relu', padding='same'))
model.add(keras.layers.MaxPooling2D(2))

최종적으로 만들어지는 피처맵의 크기는 (7, 7, 64)

Flatten Layer, Dense Layer, Dropout 추가

#Flatten layer, Dense layer 추가, hidden layer와 output layer 사이의 Dropout 추가. 
#패션 MNIST  데이터셋은 클래스 10개를 분류하는 다중 분류이므로 마지막층 뉴런은 10개, 활성화함수는 softmax
model.add(keras.layers.Flatten())
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dropout(0.4))
model.add(keras.layers.Dense(10, activation='softmax')) #output layer, activate function은 softmax 

---

model.summary()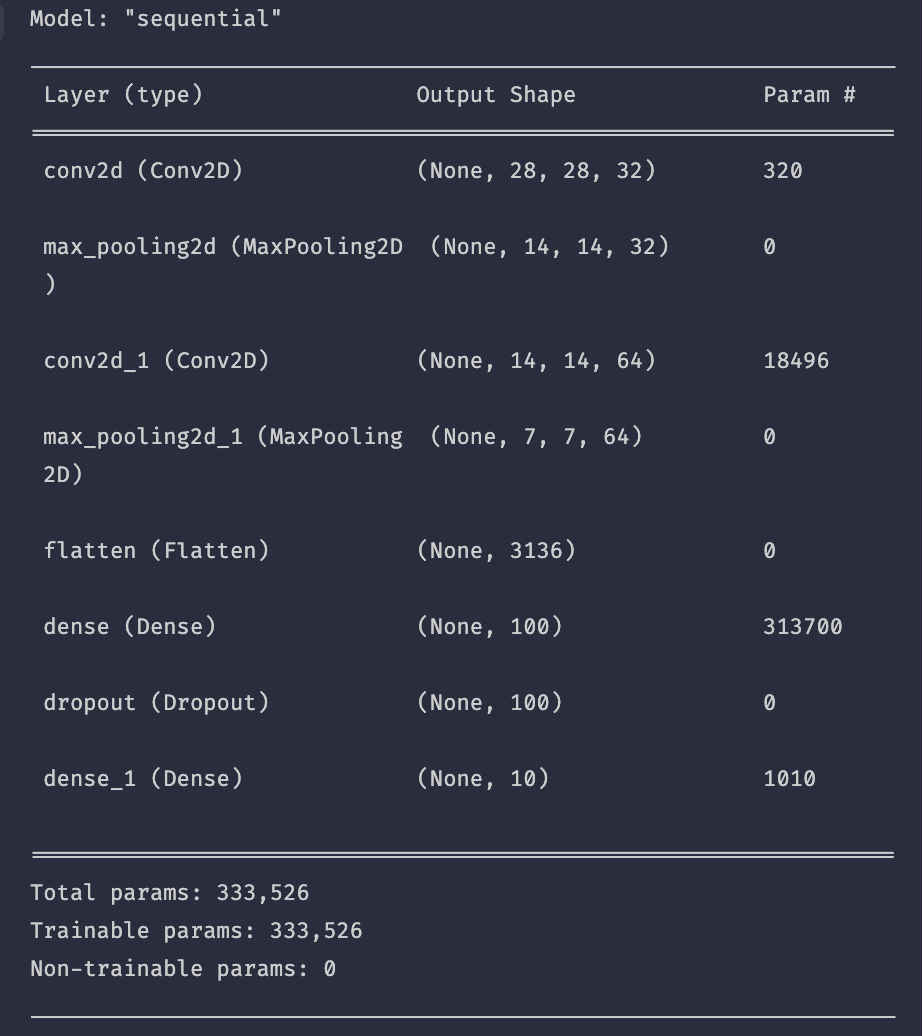

keras.utils.plot_model(model)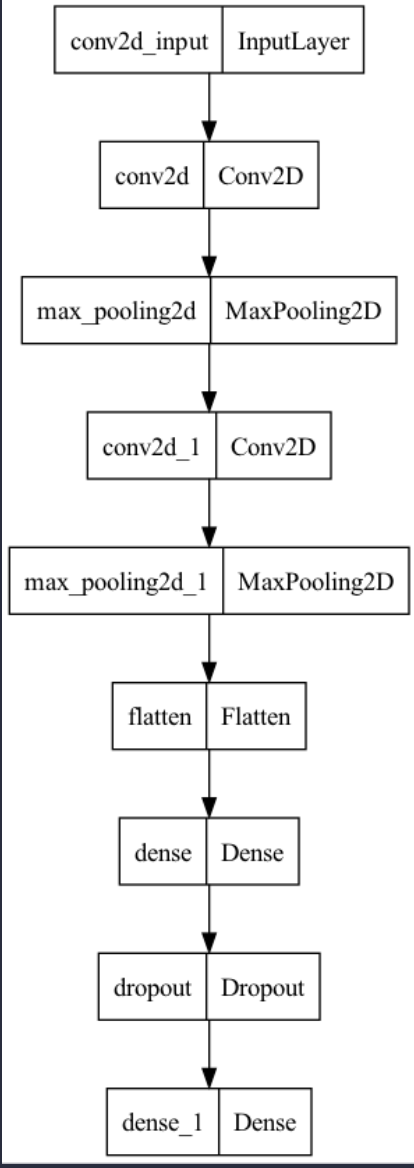

모델 컴파일과 훈련

model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics='accuracy')
checkpoint_cb = keras.callbacks.ModelCheckpoint('best_cnn-model.h5', save_best_only=True)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=2, restore_best_weights=True)
history = model.fit(train_scaled, train_target, epochs=20, validation_data=(val_scaled, val_target), callbacks=[checkpoint_cb, early_stopping_cb])

#출력
Epoch 1/20
1500/1500 [==============================] - 17s 11ms/step - loss: 0.5223 - accuracy: 0.8124 - val_loss: 0.3402 - val_accuracy: 0.8752
Epoch 2/20
1500/1500 [==============================] - 17s 11ms/step - loss: 0.3504 - accuracy: 0.8737 - val_loss: 0.3050 - val_accuracy: 0.8863
Epoch 3/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.2981 - accuracy: 0.8925 - val_loss: 0.2612 - val_accuracy: 0.9024
Epoch 4/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.2670 - accuracy: 0.9030 - val_loss: 0.2564 - val_accuracy: 0.9058
Epoch 5/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.2398 - accuracy: 0.9130 - val_loss: 0.2399 - val_accuracy: 0.9126
Epoch 6/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.2237 - accuracy: 0.9181 - val_loss: 0.2280 - val_accuracy: 0.9158
Epoch 7/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.2052 - accuracy: 0.9240 - val_loss: 0.2430 - val_accuracy: 0.9112
Epoch 8/20
1500/1500 [==============================] - 18s 12ms/step - loss: 0.1911 - accuracy: 0.9284 - val_loss: 0.2230 - val_accuracy: 0.9212
Epoch 9/20
1500/1500 [==============================] - 19s 13ms/step - loss: 0.1749 - accuracy: 0.9346 - val_loss: 0.2289 - val_accuracy: 0.9194
Epoch 10/20
1500/1500 [==============================] - 19s 12ms/step - loss: 0.1623 - accuracy: 0.9376 - val_loss: 0.2318 - val_accuracy: 0.9193

정확도는 90% 이상으로 상당히 높은 성능을 보여준다.

#검증
model.evaluate(val_scaled, val_target)

#출력
375/375 [==============================] - 2s 4ms/step - loss: 0.2230 - accuracy: 0.9212
[0.22298048436641693, 0.9212499856948853]

하나의 데이터 예측 후, 모든 케이스에 대한 확률 확인하기.

preds = model.predict(val_scaled[0:1])
print(preds)

#출력
1/1 [==============================] - 0s 45ms/step
[[2.8726700e-20 5.2744390e-30 1.1897561e-22 1.9612064e-25 1.8187563e-21
  2.3631663e-19 4.3168609e-22 1.1876107e-23 1.0000000e+00 1.5984584e-23]]

아홉 번째 확률은 1에 근사하지만, 나머지는 0에 근사한다. 시각화 후 확인하자.

import matplotlib.pyplot as plt

plt.bar(range(1, 11), preds[0])
plt.show()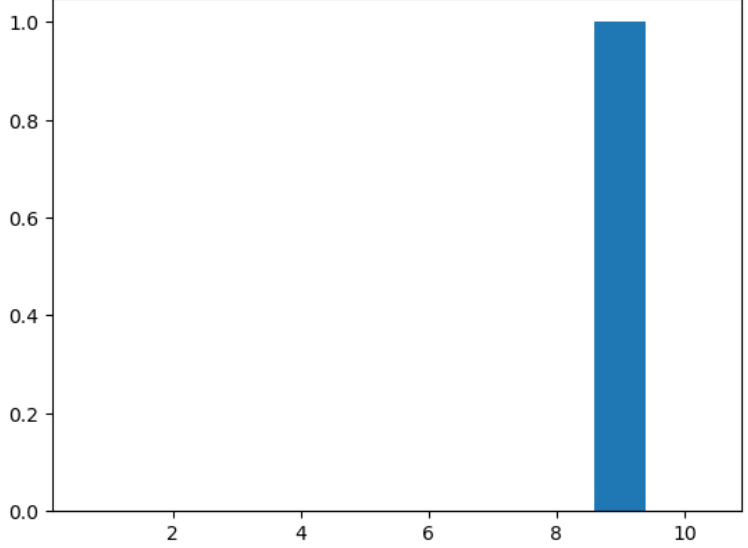

완벽하게 아홉 번째 클래스로 예측했다는 것을 알 수 있다.

#테스트
test_scaled = test_input.reshape(-1, 28, 28, 1) / 255.0
model.evaluate(test_scaled, test_target)

#출력
test_scaled = test_input.reshape(-1, 28, 28, 1) / 255.0
model.evaluate(test_scaled, test_target)

성능은 대부분 90%가 넘는 것으로 보인다.