이 포스트는 ⌜혼자 공부하는 머신러닝+딥러닝⌟ 도서를 참고하여 작성하였습니다.

1. 로지스틱 회귀

(1) 로지스틱 회귀

로지스틱 회귀 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는 데 사용되는 통계 기법이다. 분류 모델을 만드는데 사용되며, 선형 회귀로 동일하게 선형 방정식을 학습한다.

1) 시그모이드 함수(sigmoid function)

시그모이드 함수는 $y = (1+e^{-x})^{-1}$이며, 결과값 보정을 위해 사용한다. 음의 무한대로 가면 함숫값은 0에 수렴하고, 양의 무한대로 가면 함숫값은 1에 수렴한다.

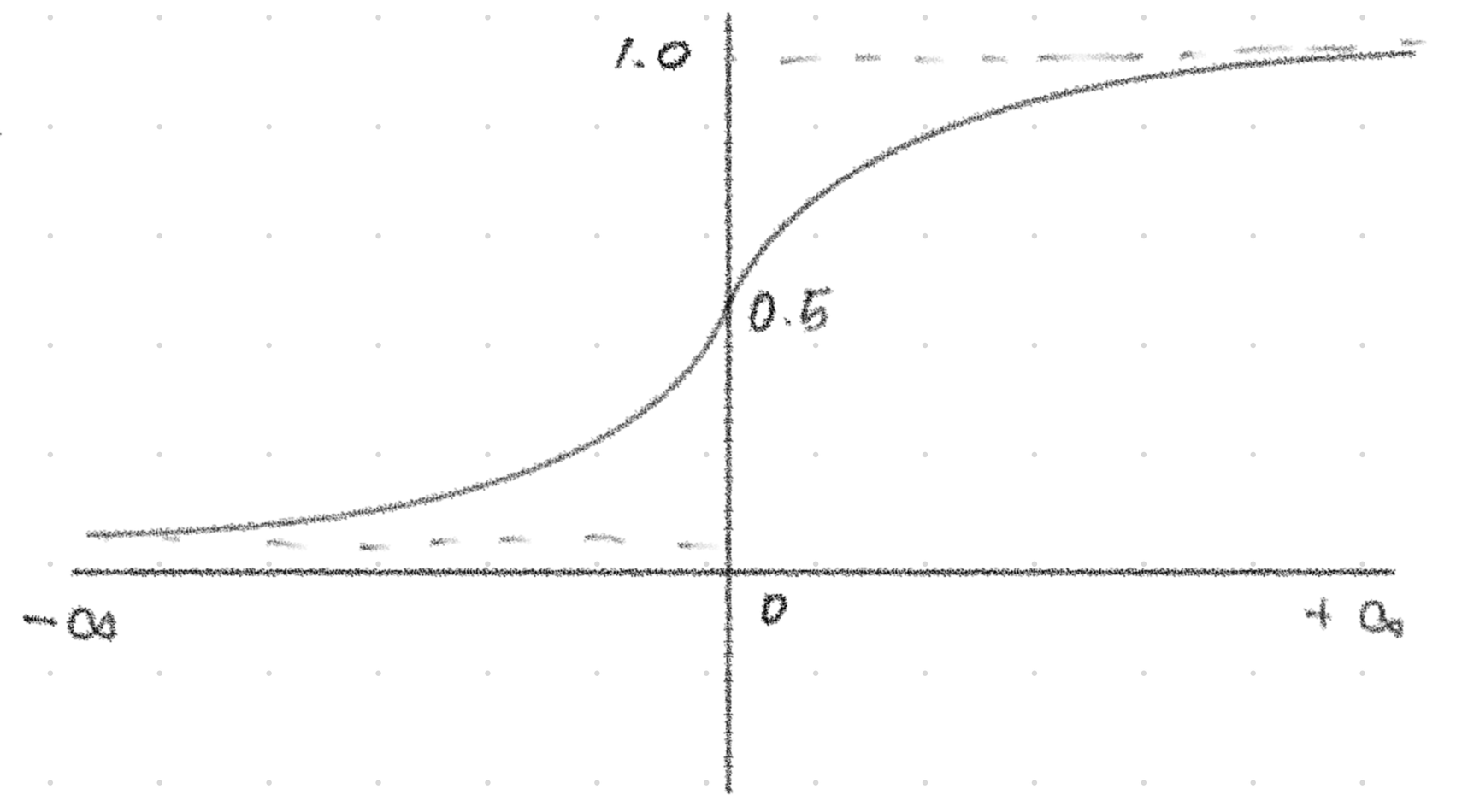
위 사진은 시그모이드 함수의 그래프를 나타낸 것이다. $x$가 아주 큰 음수일 때 0이 되고, $x$가 아주 큰 양수일 때 1이 된다.

2) 소프트맥스 함수(softmax function)

소프트맥스 함수는 세 개 이상으로 분류하는 다중 클래스 분류에서 사용되는 활성화함수이다. n차원의 벡터를 입력받아 각 클래스에 속할 확률을 추정한다. 시그모이드 함수와 다르게 확류르이 총합이 1이므도, 어떤 분류에 속할 확률에 대해 정확히 알 수 있다.

3) 하이퍼볼릭 탄젠트 함수(tanh)

하이퍼볼릭 탄젠트 함수는 시그모이드 함수과 비슷하다고 생각할 수 있지만, 엄연히 다르다. -1 ~ +1의 범위를 가지며, 미분 최댓값이 1이라는 특성으로 인해 기울기 소실에 대한 문제도 일부 해결할 수 있다.

위 사진은 하이퍼볼릭 탄젠트 함수의 그래프를 나타낸 것이다.

2. 확률적 경사 하강법

(1) 경사 하강법(Gradient Descent)

계속해서 가장 낮은 곳으로 가는 방법을 경사 하강법이라고 한다. 가장 빠른 길을 택하며, 직관적으로는 경사가 가장 가파른 길을 말한다. 하지만, 실제로 내려올 떄는 천천히/조금씩 내려오는 방법이다. 이는 경사 하강법 모델을 훈련하는 과정이다.

1) 경사 하강법의 치명적인 문제

극솟값(local minima) 문제

우리가 찾으려고 하는 것은 최솟값(global minimum)이다. 하지만, 어떤 이유로 인해서 극솟값(local minima)에 빠지는 경우 탈출하지 못하고 거기로 수렴할 수 있다.

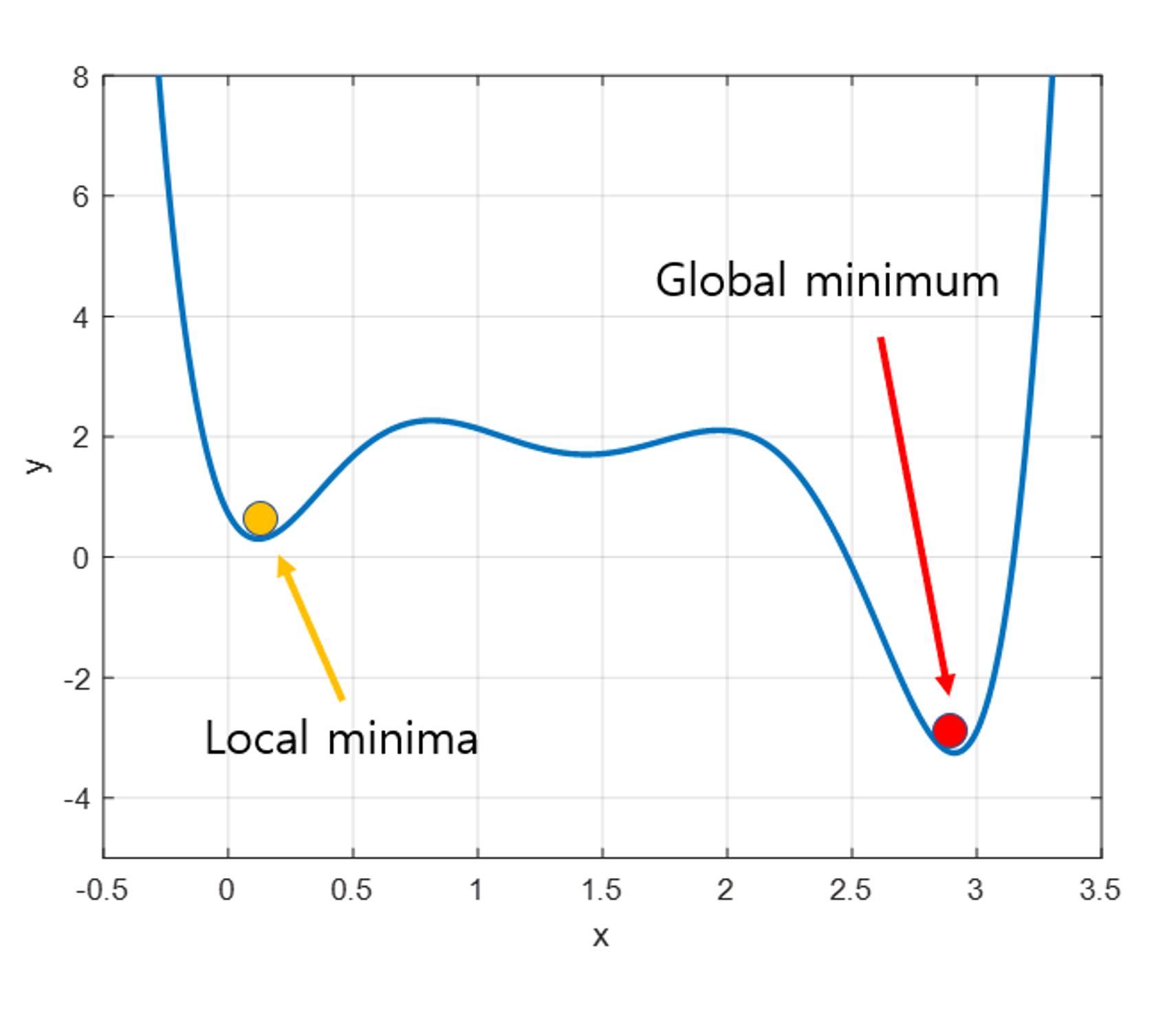
위 그림은 극솟값(local minima)와 최솟값(global minimum)을 나타낸 그림이다.

2) 확률적 경사 하강법

확률적 경사 하강법은 훈련 시 전체 샘플을 사용하지 않고 하나의 샘플을 랜덤하게 골라 가장 가파른 길을 찾는다.

3) 그 밖의 경사 하강법

• 미니배치 경사 하강법 : 여러 개씩 꺼냄
• 배치 경사 하강법 : 몽땅 한 번에 꺼냄

(2) 손실 함수(loss function)

손실 함수는 머신러닝 모델을 학습할 때 정답값과 예측값의 오차를 계산해주는 함수를 말한다. 머신러닝에서 모델이 나타내는 확률 분포와 데이터가 따르는 실제 확률 분포 사이의 차리를 나타내는 함수이다. 작을 수록 그 모델이 좋다는 것을 의미한다.

1) 크로스엔트로피 손실함수(crossentropy loss function)

엔트로피(entropy)는 불확실성의 척도로, 정보이론에서의 엔트로피는 불확실성을 나타내며, 엔트로피가 높다는 것은 정보가 많고 확률이 낮다는 것을 의미한다.