[자율주행] 3D LiDAR - camera calibration

이진호·2024년 11월 5일

자율주행

목록 보기

7/8

안녕하세요. 오랜만에 글을 작성하는 것 같습니다. 1학기엔 학교 수업, 방학때는 대학원 입시에 집중하느라 자율주행에 관한 공부를 하지 못하였습니다.

기존에 작성한 글들은 저 나름대로 공부와 스펙을 위해서 편하게 작성하였습니다. 그런데 생각보다 많은 관심과 조회수를 기록하니 더 이상 편하게 작성하지 못하겠네요. 하하. 그리고 기존에 썼던 글들을 보면서 읽기 너무 불편하다는 생각이 들었습니다. 앞으로는 최대한 쉽고 이해가 되게끔 작성해보겠습니다.

오늘 작성할 글은 camera lidar calibration에 대해서 작성하도록 하겠습니다. 지난번에 작성한 글은 2D lidar이기도 하고, solvePnP라는 방식을 사용하였습니다. 이번에는 3D lidar와 좌표계 변환 방식을 사용하여서 calibration을 사용하였습니다.

1. 사용한 방법

결론부터 말씀드리자면, 저는 이번에 cv::projectPoints() 함수를 사용하였습니다.(https://docs.opencv.org/3.4/d9/d0c/group__calib3d.html)
해당 함수에 대해서 알아보겠습니다.

Input
objectPoints: 실제 월드좌표인 lidar 좌표를 말합니다.
rvec: OpenCV에서는 3D 점들이 카메라 좌표계에서 어떻게 회전하는지를 계산합니다. 즉, 월드 좌표계를 돌려서 카메라 좌표계와 일치시키는 rotation matrix입니다.
tvec: 카메라와 라이다 좌표계의 이동 행렬을 말합니다.
cameraMatrix: 카메라의 내부(intrinsic) 파라미터를 말합니다.
distCoeffs: 왜곡 계수를 말하는데, 정확히 어떤 왜곡 계수인지는 잘 모르겠습니다. 아마 카메라 내부 파라미터의 왜곡 계수라기보단 어안 카메라와 같은 왜곡 계수를 말하는 것 같습니다. 저는 평범한 웹캠일 뿐만 아니라, 시뮬레이션 상에서 진행하였기 때문에 왜곡 계수를 0으로 설정하고 진행하였습니다.
Output
imagePoints: 위 input값들을 이용해서 projection을 진행한 이미지 좌표들이 해당 배열에 저장됩니다.

Input의 결과 값들을 넣으면 projection 된 output 값들이 자동으로 나옵니다. solvePnP보다 좀 더 정확한 값들이 나와서 해당 함수를 진행하게 되었습니다.

하지만 몇 가지 단점이 존재합니다.

첫 번째로 센서들의 정확한 원점을 구할 수 없습니다. 시뮬레이션은 원점의 좌표들이 정확하게 나와있어서 쉽게 구현할 수 있으나, 실생활에는 그렇지 않습니다. 실제 센서들의 내부를 볼 수 없으니 원점이 정확히 어디인지 계산할 수 없습니다. 미세한 오차가 존재한다는 말이죠.
두 번째로는 센서가 조금이라도 움직이면 쓸 수 없게 됩니다. 해당 함수는 회전 행렬과 이동 행렬을 사용합니다. 센서가 조금이라도 움직이게되면 회전 행렬과 이동 행렬 값 모두 변하게 됩니다. 그렇게 되면 결과 값도 엉망이 되겠죠.

해당 단점들을 모두 극복할 수 있는 환경인 시뮬레이션은 가장 적합한 환경입니다. 저는 Morai 시뮬레이션을 통한 대회를 진행하기 때문에 이러한 단점들은 고려하지 않았습니다.

실제 세계에서는 센서들을 단단하게 고정하거나 targetless 방법을 사용하면 좋을 것 같습니다. (저도 해본 적은 없습니다.)

그러면 해당 함수들을 이용한 Input들을 하나씩 보겠습니다.

2. objectPoints

말 그대로 라이다 좌표들의 배열입니다. x, y, z 값을 cv::Point3f로 저장한 vector 배열들을 사용하는 std::vector<cv::Point3f>의 자료형을 사용하였습니다. 라이다 값은 raw data를 바로 사용하는 것이 아닌 전 게시글인 '[자율주행] 자율주행을 위한 3D LiDAR Process'을 통해 전처리를 완료한 라이다 좌표 값들을 저장하였습니다.(ROI->Voxel->RANSAC->DBSCAN) 해당 방법을 사용하여도 좋고 딥러닝을 활용한 라이다 값을 사용하여도 좋습니다. 월드 좌표계에 해당하는 좌표만 있으면 됩니다.

원본 velodyne points
전처리를 완료한 lidar pre

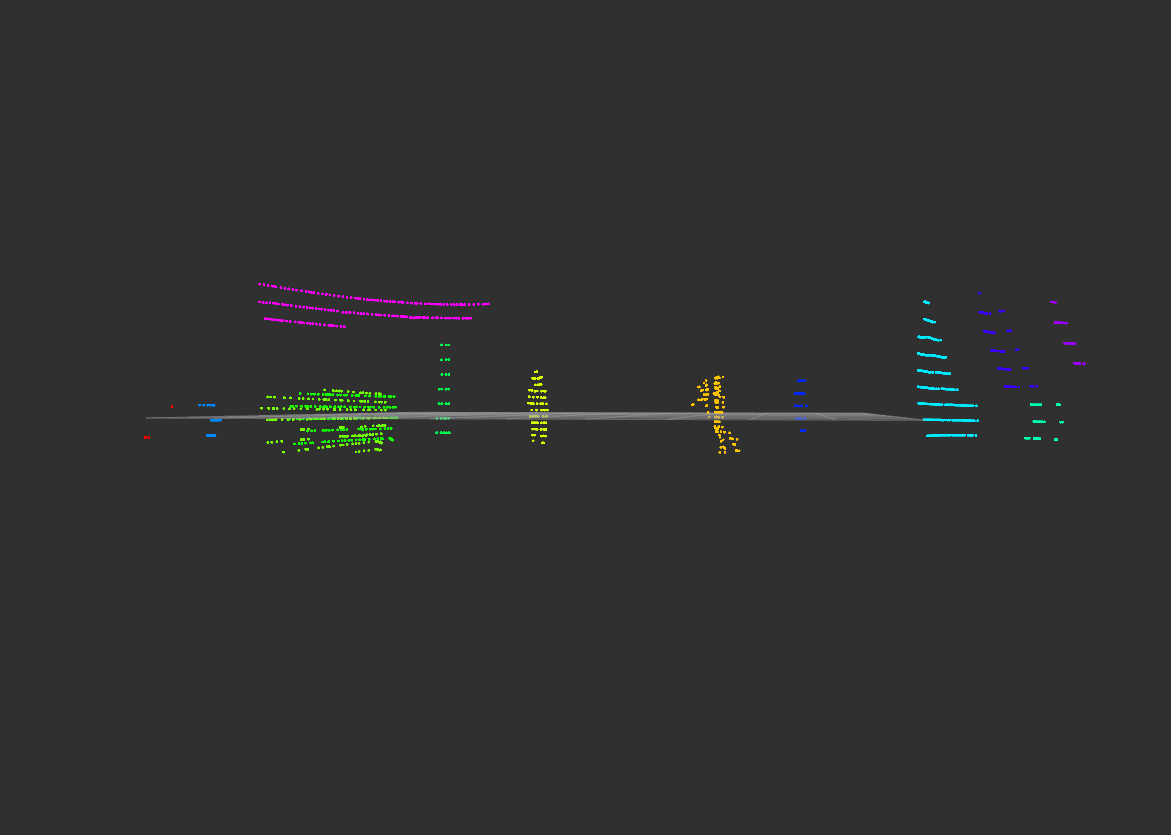
3. rvec

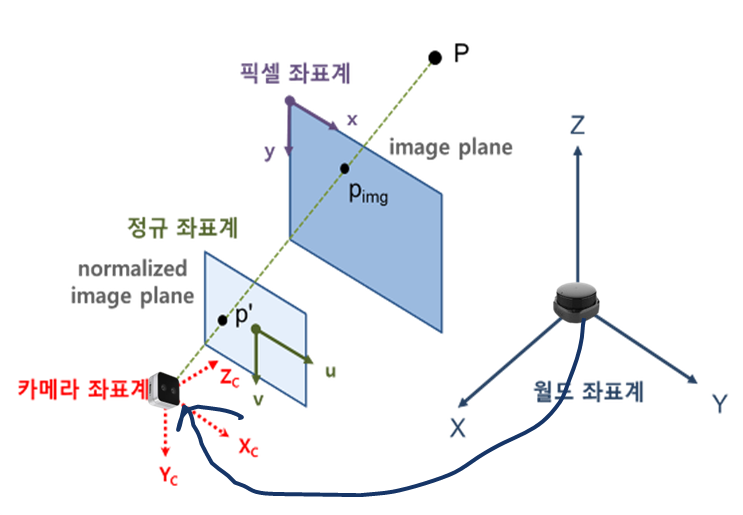
해당 과정은 위의 그림의 화살표와 같습니다.
rvec는 lidar좌표계와 camera좌표계 간의 회전(rotation)를 말합니다. Rotation matrix 공식을 통해서 구할 수 있습니다.(https://en.wikipedia.org/wiki/Rotation_matrix)

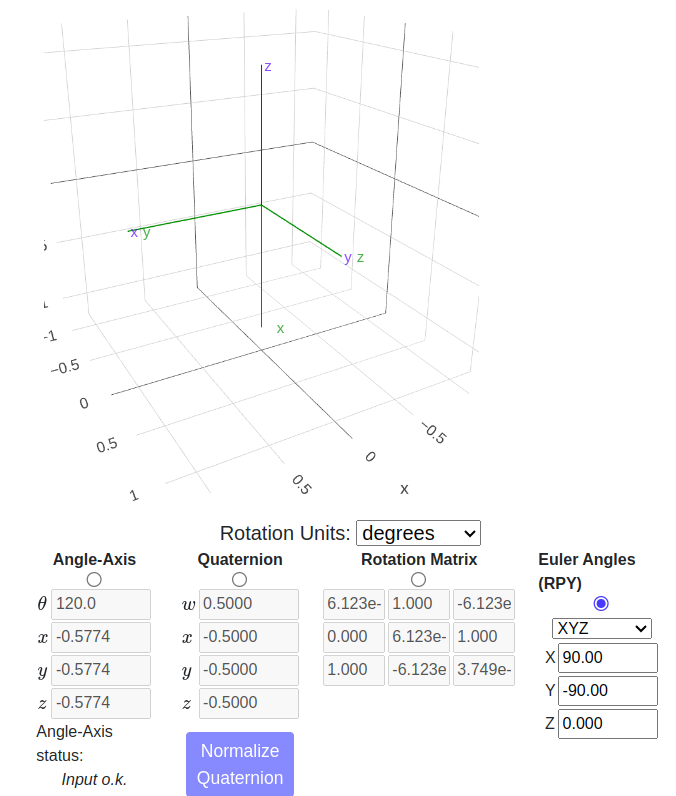
해당 그림은 파란색인 월드 좌표계를 roll 90도, pitch -90도 회전하여서 초록색인 카메라 좌표계로 만든 것 입니다. 카메라와 라이다가 같은 방향을 보고 있다면 해당 값이 끝입니다.
만약 카메라가 돌아가 있다면, 해당 값에서 rotation matrix 공식을 다시 곱하면 쉽게 구할 수 있습니다.

// 라이다 -> 카메라 좌표계로 일치시키는 행렬
rvec = (cv::Mat_<double>(3, 3) << 1, 0, 0,
                                  0, 1, 0,
                                  0, 0, 1);
rvec = rvec * this->computeRotationMatrix(90, -90, 0);
    
// 카메라의 yaw값이 15도 돌아가있는 rotation matrix
rvec = rvec * this->computeRotationMatrix(0, 0, 15);

4. tvec

이동 행렬 입니다. 라이다 좌표와 카메라 좌표가 얼만큼 떨어져 있는지에 대해 구하면 됩니다. 단순히 x, y, z 값을 이용하여 구할 수 있습니다. 즉, $tvec = lidar_{x, y, z} - camera_{x, y, z}$ 를 통해서 구할 수 있습니다.

tvec = (cv::Mat_<double>(3, 1) << lidar_x - camera_x, lidar_y - camera_y, lidar_z - camera_z);

5. cameraMatrix

카메라의 내부(Intrinsic)파라미터 값 입니다. openCV와 checkerboard를 통해서 쉽게 구할 수 있습니다.
저는 시뮬레이션을 사용하기 때문에 카메라 내부 파라미터 값이 제공되어 쉽게 이용할 수 있었습니다.
내부 파라미터의 값들을 하나씩 다시 보겠습니다.

$f_{x}, f_{y}$ : focal length인 초점 거리입니다. 단위는 거리이지만 pixel입니다. 이미지 pixel은 이미지 센서의 cell에 대응되기 때문에 거리를 구할 수 있습니다. 현대의 기술이 많이 발전하여서 $f = f_{x} = f_{y}$ 값으로 두어도 됩니다.
$c_{x}, c_{y}$ : Principal point인 주점입니다. 카메라 렌즈의 중심을 뜻 합니다. 이것 또한 현대 기술이 발전하여서 절반에 해당하는 값을 넣어주면 됩니다. 예를 들어, 640x480인 경우, $c_{x} = 320, c_{y} = 240$ 의 값에 해당합니다.
$skew_c$ : skew coefficient인 비대칭 계수입니다. 이미지 센서의 cell array의 y축으로 기울어진 정도를 뜻합니다. 이 역시도 현대 기술이 발전하여 0으로 설정하여도 무방합니다.

더 정확한 값을 원하시면 말씀드린대로 checkerboard를 통해서 구할 수 있습니다.

이런식으로 시뮬레이션에서 카메라의 내부 파라미터 값을 제공합니다. 이를 통해서 쉽게 구할 수 있습니다.

다만, 해당 값들은 문제가 있습니다. 바로 FOV(Field of View)에 따라서 focal length 값이 반영되지 않는다는 점입니다. 해당 값은 FOV가 90도인 값 입니다. FOV가 변한다면 FOV를 통해서 focal length를 직접 구해야 합니다.

FOV 공식은 다음과 같습니다.
$FOV = 2 \times tan^{-1}(\frac{h}{2f})$ , 여기서 h는 이미지의 높이(height)이고 f가 focal length입니다.

따라서 focal length 공식은 다음과 같습니다.
$f = \frac{h}{2 \times tan(\frac{FOV}{2})}$

// 각도를 라디안으로 변환하는 함수
double deg2rad(double degrees) {
    return degrees * (M_PI / 180.0);
}

double fov = 60.0; // Field of View
// focal length
double fx = 640.0 / (2 * std::tan(deg2rad(fov/2)));
double fy = fx;

// principal points
double cx = 320.0;
double cy = 240.0;

// skew coefficient
double skew_c = 0;
    
cameraMatrix = (cv::Mat_<double>(3, 3) << fx, 0, cx,
                                            0,fy, cy,
                                            0, 0, 1);

6. distCoeffs

왜곡 계수를 뜻합니다. 말씀드린대로 정확히 어떤 값인지는 모르겠습니다. 저는 시뮬레이션을 사용하여서 0으로 설정하였습니다. 이는 distCoeffs = cv::Mat::zeros(4, 1, CV_64F); 으로 값을 넣을 수 있습니다.

    distCoeffs = cv::Mat::zeros(4, 1, CV_64F); // 왜곡 없음

7. Output: imagePoints

해당 값들을 이용해서 이미지에 투영시킨 픽셀 값들 입니다. 이는 std::vector<cv::Point2f> imagePoints; 배열 값에 저장할 수 있습니다. 이를 cv::circle과 같은 함수를 이용하여 이미지에 나타낼 수 있습니다.

// 이미지 포인트를 저장할 벡터
std::vector<cv::Point2f> imagePoints;
            
// 3D 포인트를 2D 이미지 평면으로 투영
cv::projectPoints(lidar_points, rvec, tvec, cameraMatrix, distCoeffs, imagePoints);
            
for (size_t i=0; i < imagePoints.size(); i++)
{
    const auto& imagePoint = imagePoints[i];
    int x = static_cast<int>(imagePoint.x); // X 좌표
    int y = static_cast<int>(imagePoint.y); // Y 좌표

    cv::circle(copy_frame, cv::Point(x, y), 3, cv::Scalar(0, 0, 255), -1); // 점 찍기
}

투영 결과

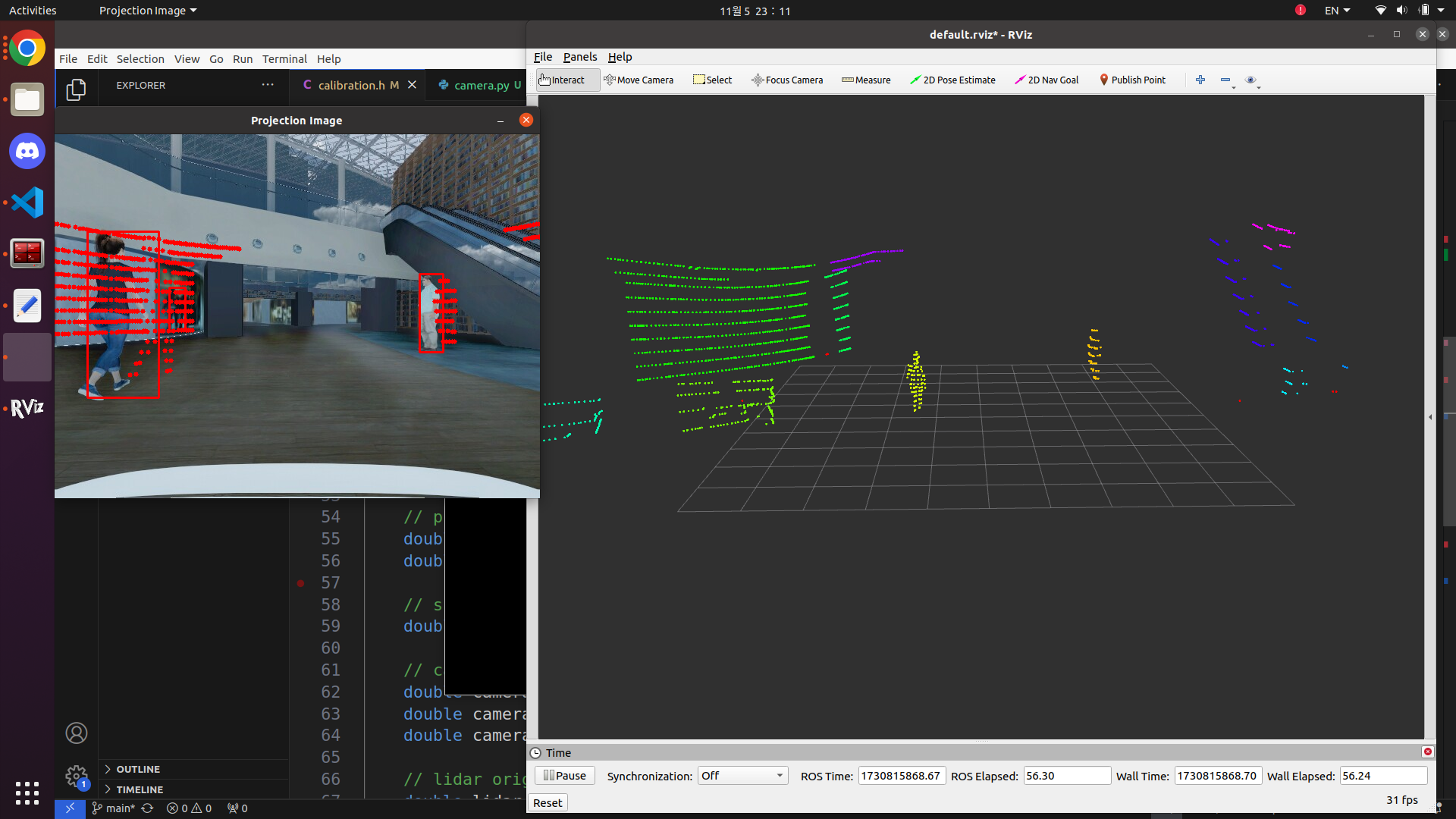
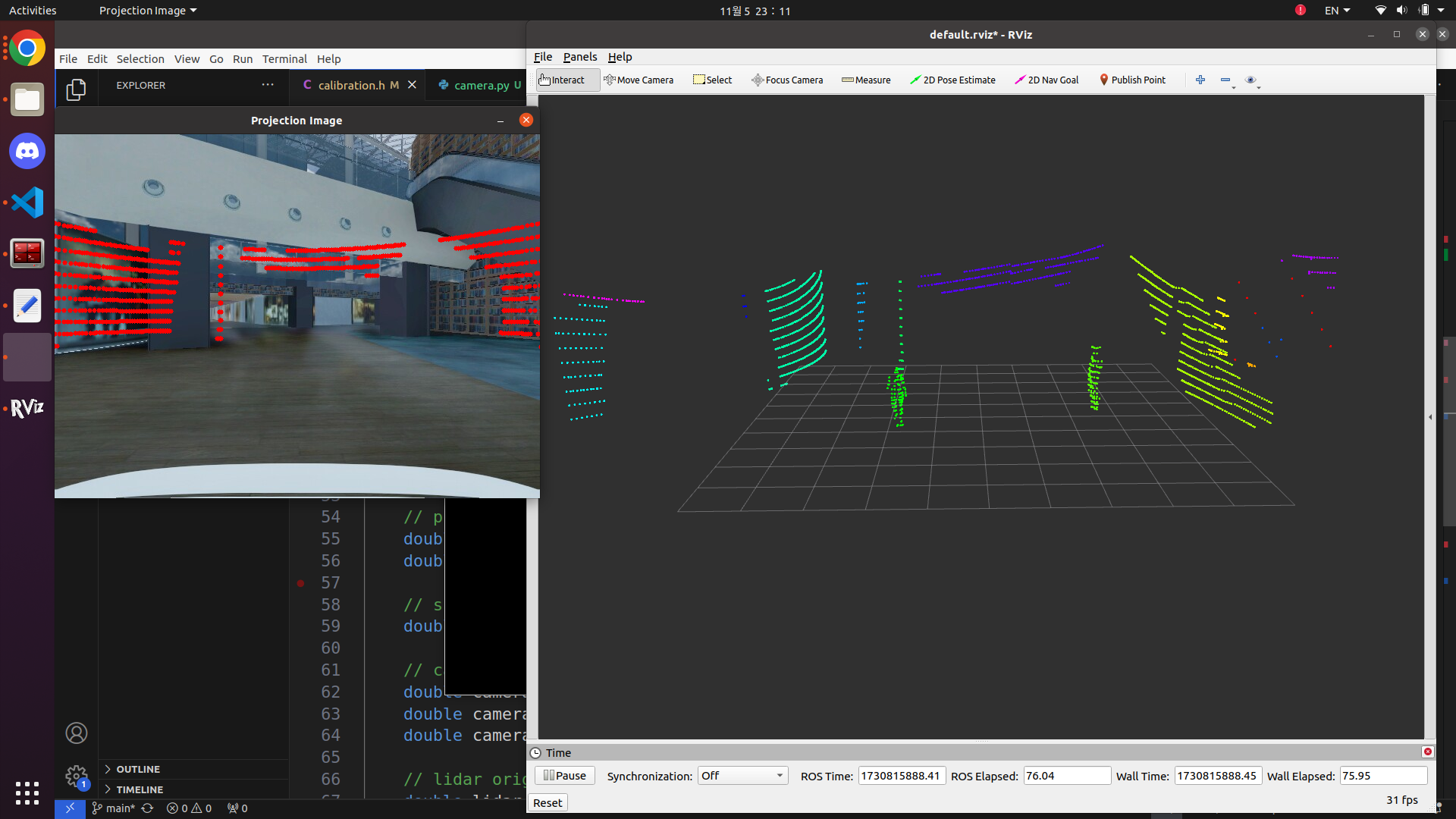
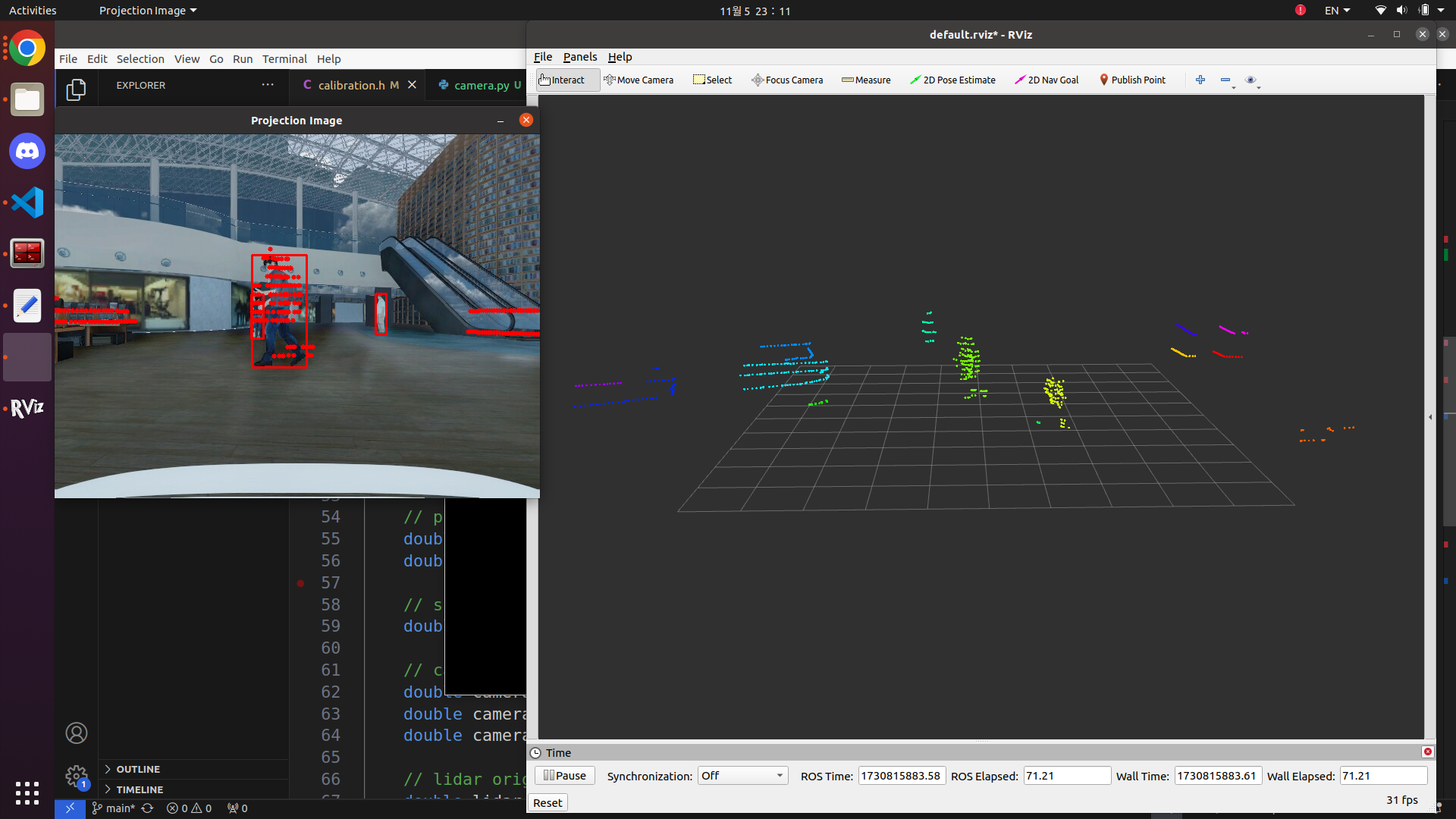
해당 결과는 fov 90으로 설정하여 만든 결과입니다. 보시는 것처럼 투영하는데 있어서 딜레이가 살짝 있지만 주행하는데 있어서 큰 문제는 없었습니다. 밀리는 원인은 저도 잘 모르겠네요ㅠㅠ

rqt_graph는 다음과 같습니다. 코드는 아래에 첨부하도록 하겠습니다.
(https://github.com/jinhoyoho/camera_3dlidar_calibration)

느낀점

대회 복장입니다만,... 조끼를 왜 주는지 잘 모르겠네요.
해당 대회가 C++을 이용한 첫 프로젝트입니다. 해당 대회를 통해서 C++ 실력이 정말 말도 안되게 상승한 것 같습니다. 역시 실력을 높이는데는 프로젝트가 최고입니다.

자율주행은 항상 어려운 것 같습니다. 인식만 잘 한다고 되는 것도 아니고, 제어만 잘 한다고 되는 것도 아니죠. 모두 다 합이 맞아야, 비로소 자율주행이 동작하는 것 같습니다. 그만큼 어렵기 때문에 아직까지도 연구가 활발히 진행되고 있죠.

AI는 최근에 각광을 받은 학문입니다. 이에 대한 명확한 관련 서적이나 학교 커리큘럼이 이제야 서서히 윤곽이 잡히는 듯 보입니다만(CS231, 밑바닥부터 시작하는 딥러닝, DeepLearningBook(Ian Goodfellow) 등등), 이것마저도 학교마다 다릅니다. AI와 관련된 대표적인 대학 전공 서적은 없습니다. CNN에서 transformer를 사용하듯이 사용하는 기술도 계속해서 달라지고 있습니다. 미래에는 더 좋은 기술이 틀림없이 나올 것 입니다.

자율주행에 대한 관심은 AI가 발전하면서 같이 커져갔습니다. AI에 대한 교육은 점점 윤곽이 잡히는데 반해, 자율주행에 대한 교육은 아직 없는 것 같습니다. 저 또한 자율주행에 관한 공부를 책이 아닌 인터넷이나 논문을 통해서 하였습니다. 아직 대표적인 자율주행 공부 서적이 없는 것이 안타까울 따름입니다. 물론 자율주행도 AI(computer vision)의 연장선 입니다만, 자율주행 분야의 책이나 전문적인 학교 강의가 필요하다고 생각합니다. 자율주행의 분야 또한 생긴지 얼마 안되기도 하였고, 아직 연구도 진행중이며 양산할 수 있는 뚜렷한 기술이 없으니, 교육 자료가 없는 것도 당연하다고 생각합니다. 이에 대한 지원과 관심이 미래에도 더욱 확대 될 것이라고 믿어 의심치 않습니다.

현재도 몇몇 학교에는 자율주행학과가 생기고 있습니다. 연구가 활발히 진행되고 정착되어, 더 먼 미래에는 컴퓨터공학과처럼 모든 학교에 자율주행학과가 있으면 좋겠습니다. 나중엔 저도 해당 학과의 교수가 되면 좋겠네요. 하하하

이런 저런 제 생각을 읽어주셔서 감사합니다.
다음 시간에는 신호등 처리에 대해서 말씀드리겠습니다.

질문이나 잘못된 정보는 언제든지 댓글에 작성해주세요!