출처:
Ray Tracing in One Weekend - Rays, a Simple Camera, and Background
Github - GaepoMorningEagles/mini_raytracing_in_c

---

Camera and Canvas

---

The Ray Structure

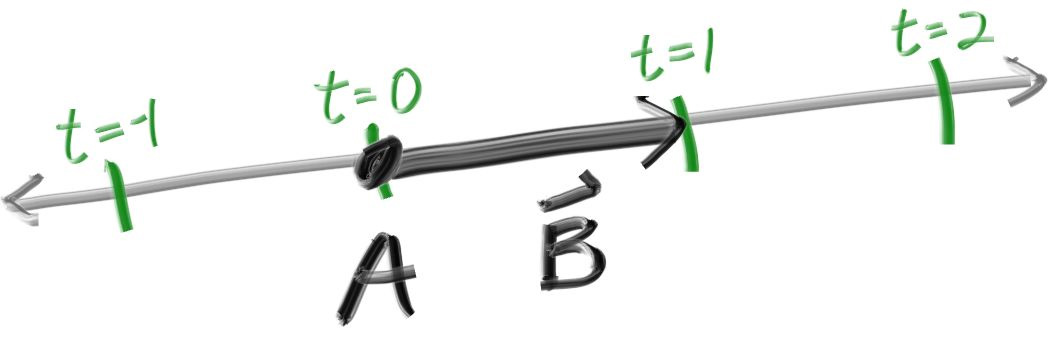
모든 광선추적기(ray tracers)에는 광선 구조체와 광선을 따라 보이는 색상에 대한 계산이 존재한다. 광선을 함수 $\bold{P}(t) = \bold{A} + t\bold{b}$ 로 생각해 보겠다. 여기서 $\bold P$는 3차원 광선 위에 존재하는 3차원 좌표(점)이다. $\bold A$는 광선의 원점이고 $\bold b$는 광선의 방향(방향 벡터)이다. 광선의 매개변수 $t$는 실수(코드에서 double형)이다. $t$의 값에 따라 $\bold{P}(t)$가 광선 위에서 움직인다. $t$가 양수라면 $\bold A$의 앞부분에서 움직이고, $t$가 음수라면 $\bold A$의 뒷부분에서 움직일 것이다. $t$가 양수일 때, half-line 또는 광선(ray)라고 한다. ray_at() 함수를 $\bold{P}(t)$ 함수라고 볼 수 있겠다.

---

Sending Rays into the Scene

광선추적기(ray tracer)는 픽셀을 통해 광선을 보내고 광선 방향에서 보이는 색상을 계산한다.
1. 눈에서 픽셀까지의 광선을 계산한다.
2. 광선이 교차하는 물체를 결정한다.
3. 해당 교차점의 색상을 계산한다.
광선추적기를 만들 때, 여기서는 코드를 시작하고 실행하기 위해 카메라를 사용한다. 그리고 간단한 그라데이션을 이용한 배경색을 반환하는 함수(ray_color())를 만든다.

x와 y를 헷갈려하지 않기 위해 정사각형이 아닌 이미지를 사용한다. 여기서는 16:9의 종횡비를 사용했다.

장면 광선을 통과할 가상의 뷰포트(viewport)를 설정해야 한다. 표준 정사각형 픽셀 간격의 경우, 뷰포트의 종횡비는 렌더링된 이미지의 종횡비와 동일해야 한다. 여기서는 뷰포트의 높이(height)를 2로 고정했다. 그리고 투사 평면과 투사 점 사이의 거리를 하나의 단위로 설정하여 이를 초점 거리(길이)(focal length)라고 한다. 나중에 나올 focus distance(초점 거리)와 혼동하지 말아야 한다.
(viewport를 설정하고 사용해야 하는 이유에 대해서 의문이 들었었다. 내가 내린 결론?답?은 다음과 같다.

위의 캠코더 사진을 가지고 설명해보겠다. 사람이 그냥 눈으로만 봐도 공간은 상하좌우에 쫙 깔려 있는데, 시야는 한정되어 있어서 본인의 뒤쪽은 보지 못한다. 이처럼 캠코더의 카메라 렌즈 부분이 뷰포트라고 하면, 우리는 뷰포트를 통해 들어오는 장면만 보게 된다. 그리고 그 장면은 캔버스라고 표시한 부분에 나타나게 된다. 나는 자꾸 캔버스를 공간상에 두고 이상한 생각을 했는데, 캔버스를 공간과 분리하니까 훨씬 생각하기가 편했다.)

카메라의 좌표를 (0, 0, 0)에 배치한다. 아래 그림에서처럼 y축은 위로, x축은 오른쪽으로 이동한다.(양의 방향) 오른손 좌표계의 법칙을 따르기 위해 z축은 카메라를 향하는 방향이 양의 방향이다.(카메라에서 광선이 뻗어나가는 방향이 음의 방향) 왼쪽 상단 모서리에서 화면을 가로지르고, 광선의 끝 점을 화면을 가로질러 움직이기 위해 화면의 측면을 따라 두 개의 오프셋 벡터를 사용한다.

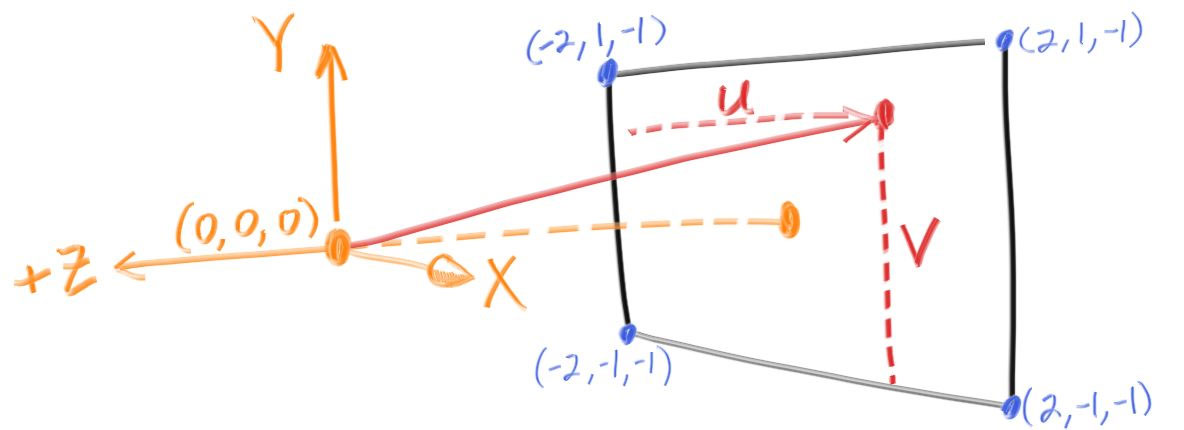
코드를 해석하면, 종횡비가 16:9인 캔버스가 설정되어 있고 이와 같은 종횡비를 가진 뷰포트의 높이를 2.0으로 고정해서 뷰포트의 크기를 설정했다. 초점거리는 1.0이고 따라서 뷰포트는 $z = -1$인 xy평면에 위치한다. 카메라는 (0, 0, 0)에 위치한다. 그리고 뷰포트의 왼쪽 아래의 코너점 좌표를 다음과 같이 설정했다.

나는 이렇게만 보면 잘 이해가 안 가서, 다음과 같이 생각했다.

또 왼쪽 아래 코너점의 좌표를 구하는 것인데 자꾸 벡터로 생각해서 헷갈렸다. 좌표점으로 생각하고 연산하면 편하다.

카메라에서 나오는 초기 광선은 카메라의 좌표(원점)에서 시작하며, 위에서 구한 왼쪽 아래 코너점의 좌표에서 가로와 세로에 각각 곱해 준 u, v만큼 이동한 좌표를 가리키는 단위벡터이다.

ray_color()에서는 y좌표를 기준으로 그라데이션을 준다.($-1.0 < y < 1.0$) 벡터를 정규화한 후에 y좌표의 높이를 보기 때문에, 수직 그라데이션 외에 수평으로도 그라데이션이 생긴다는 것을 알 수 있다. 색상의 범위는 $[0,1]$이기 때문에 이를 맞춰주기 위해, t의 값이 이 범위 안에 들어가게 해 주었다.
$-1.0 < y < 1.0$
$0.0 < y + 1 < 2.0$
$0.0 < (y + 1) / 2 = t < 1.0$
그리고 t의 값에 따라서, 흰색과 하늘색의 가중치를 다르게 줘서 아래의 결과 그림과 같은 하늘이 나타나게 했다.

---

Result Image