Is Learning Feasible?

이번 주제는 과연 학습한다는것이 실현 가능한지 이론적으로 알아보겠다.

$\to$ PAC-Learnable 한가?
(Probably, Approximately, Correct)

---

먼저 한가지 예제를 살펴보자.

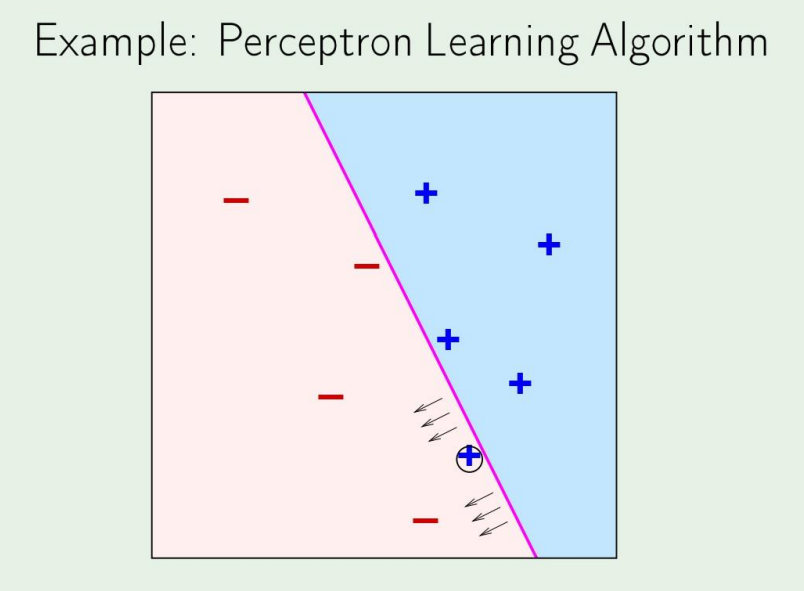
이러한 간단한 분류 알고리즘이 있다고 하자. 그렇다면 저 동그라미친 +가 존재하더라도 어느정도 우리는 분류를 진행할 수 있을것이다.

ML이란 data driven approach이기 때문에, data를 계속 넣으면서 학습을 진행한다.
그런데, target function이 존재하는건 알지만, target function을 모르기때문에 data를 계속 넣어가면서 우리가 그 function을 찾는것이다.

여기서 약간 의문점이 발생한다.
모르는 target function을 과연 data를 많이 넣는다고해서 알수있을까?
즉 수많은 data를 넣어도 정답을 모르니까 과연 이게 맞는가? 라는 생각을 할수있다.

그렇다면 이 모르는데 학습할수 있는 근거는 과연 무엇인가를 알아볼것이다.

---

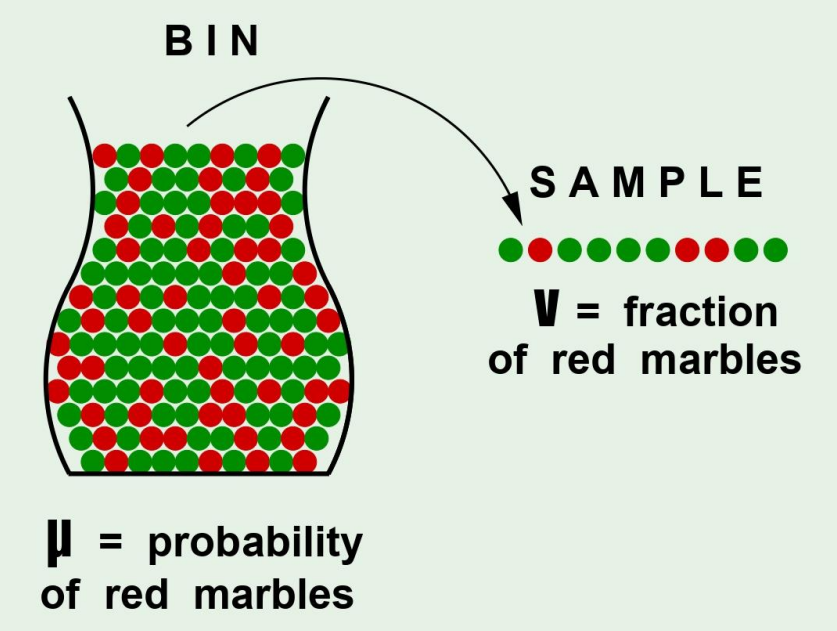
우리가 그룹화된 샘플이 이렇게 존재한다고 해보자.
빨간 공이 뽑힐 확률을 $\mu$라고 하면 초록 공이 뽑힐 확률은 $1-\mu$로 나타낼 수 있다.

그리고 샘플을 뽑고, 그 샘플에서 빨간공이 뽑힐 확률을 $\nu$라고 하자.

more general하게 생각을 하면, 빨간 공을 뽑는다는 것을 wrong guess, 즉 잘못 예측한 value값이라고 생각하자

Does $\nu$ say anything about $\mu$?

답은 Yes or no일것이다.
No라고 생각했다면 만약 병안에 딱 10개의 초록공이 있고 나머지는 모두 빨간공이라고 하였을때, sample이 모두 초록색일 확률이 존재한다.
따라서 sample로 전체를 예측한다는게 말도 안된다고 말할수도있고,
Yes라고 생각했다면, sample을 많이 뽑아서 평균을 내게 된다면, 전체와 비슷해진다고 생각할수도있다.

답은 둘다 맞다!

• No: 샘플로 전체를 알수없는것은 당연하다
• Yes: not absolutely certain but almost certain!

What does $\nu$ say about $\mu$?

그렇다면 sample은 무엇을 말해줄까?

In a big sample (large $N$), $\nu$ is probably close to $\mu$ (within $\epsilon$)

이는 위대한 발견중 하나인 Hoeffding's Inequality 이다.
식은 다음과 같다.

여기서 $|\nu - \mu|$는 bad event로, sample과 전체의 차이가 줄었으면 좋겠다고 생각할 수 있다.
부등식의 오른쪽을 보면, $N$은 number of sample로, 많이 뽑게 된다면 sample과 전체가 같아지게 된다.

그리고 우리는 이제 $"\mu = \nu"$ is P.A.C 할때 같다고 할 수 있다.

Hoeffding's Inequality의 좋은점은 bound가 더이상 우리가 알수없는 값인 $\mu$로 표현되지 않는다는 것이 매우 중요하다.
그러나 $N$과 $\epsilon$과의 trade off 문제가 존재한다.

Connection to learning

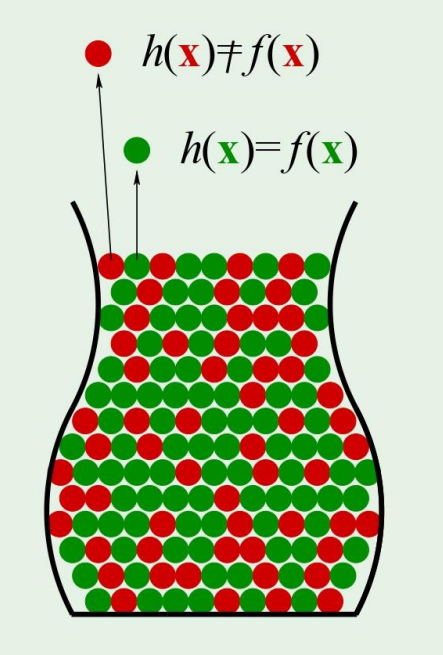
처음에는 모든 공이 회색인데, 다음처럼 공의 색을 정한다고 해보자.
Each marble ${\color{Gray} \bullet }$ is a point $x \in \mathcal{X}$

${\color{Green} \bullet }$ : Hypothesis got it ${\color{Green} \text{right}}$ $h({\color{Green}x })=f({\color{Green} x})$
${\color{Red} \bullet }$ : Hypothesis got it ${\color{Red} \text{right}}$ $h({\color{Red}x })\neq f({\color{Red} x})$

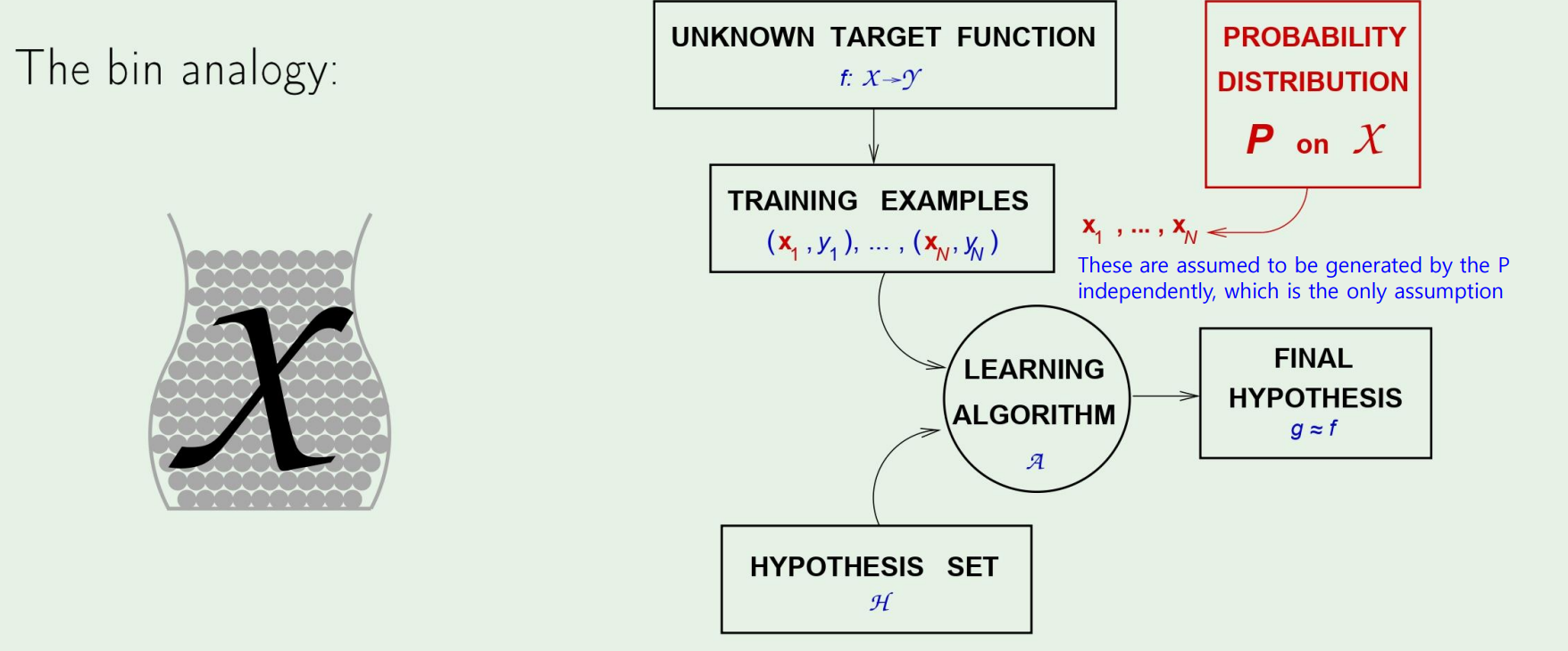
즉, 우리가 target function을 모르더라도, Hoeffding 형님에 의해서 우리의 hypothesis를 target function에 근사시킬수있다!

---

다시 우리의 원래 목표인 hypothesis h를 찾는걸로 돌아와보자.

Multiple bins

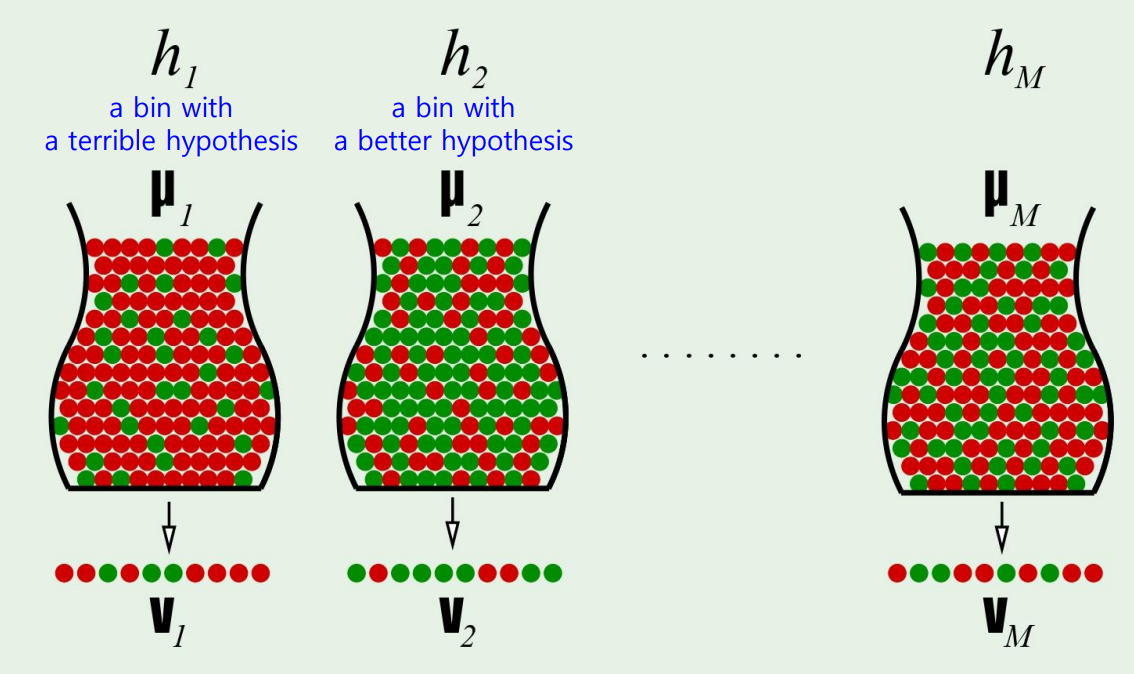
Hoeffding 형님에 의해서 우리가 충분히 괜찮은 hypothesis를 찾게 된다면, we can declare!

Notation for learning

이제 다시 용어를 정리하겠다.

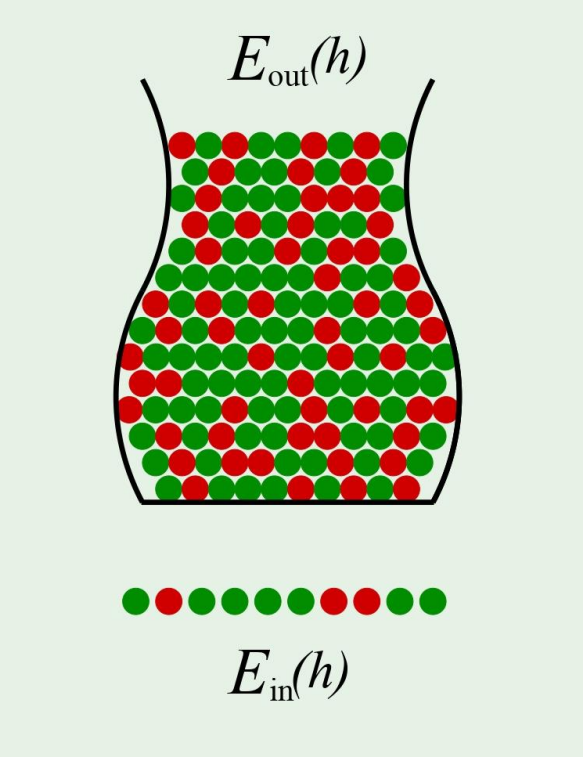
Both $\mu$ and $\nu$ depend on which hypothesis $h$,

• $\nu$ is ${\color{Purple} \text{in sample }}$ denoted by $E_{in}(h)$
• $\mu$ is ${\color{Purple} \text{out of sample }}$ denoted by $E_{out}(h)$

아까의 Hoeffding 식은 다음처럼 바뀐다.

그렇다면 이제 best hypothesis를 찾고 끝내면 될까?

그렇지 않다!

---

Hoeffding doesn't apply to multiple bins....

그렇다면 우리는 multiple bin에 대해 bound되는 값을 찾아야 한다.

이게 무슨 소리냐면, bin이 엄청 많다면 매우 확률이 극악인 hypothesis라도 bound가 엄청 loose해진다.

• 한명이 동전 10개를 던져 10개 모두 앞면이 나올 확률은 $2^{10}$ 이지만,
• 1000명이 동전 10개를 던져 모두 앞면이 나올 경우가 있는 확률은 무려 63%에 가깝다.

즉, M개의 bin이 존재한다면 그만큼 우리의 bound를 더 tight하게 잡아야 한다!

A simple solution

M개의 bin에 대해 모든 hypothesis $h_1 \sim h_m$까지가 모두 실패할 경우를 or 계산을 통해 얻어내면 된다.

The final verdict

그래서 hypothesis가 많아지게 된다면, 이제는 $M, N, \epsilon$ 이 3개의 문제로 바뀌게 된다!