The Linear Model

저번 포스팅을 리뷰하면, Learner을 디자인해서 문제를 해결하는것이 왜 Feasible한지 살펴보았다.
그렇다면 이번 포스팅에서는 이를 Linear model에 대해 살펴보겠다.

---

A real data set

우리가 잘 알고있는 MNIST data를 보자

이 데이터로 classification을 진행하게 되는데, 모호한 숫자들이 가끔식 등장한다

Input representation

MNIST data는 256개의 x input으로 이루어져있다.
그렇다면 linear model에는 256개의 $w$가 존재한다는 것이다.

근데 우리는 하나의 Feature을 다음처럼 나타내보자

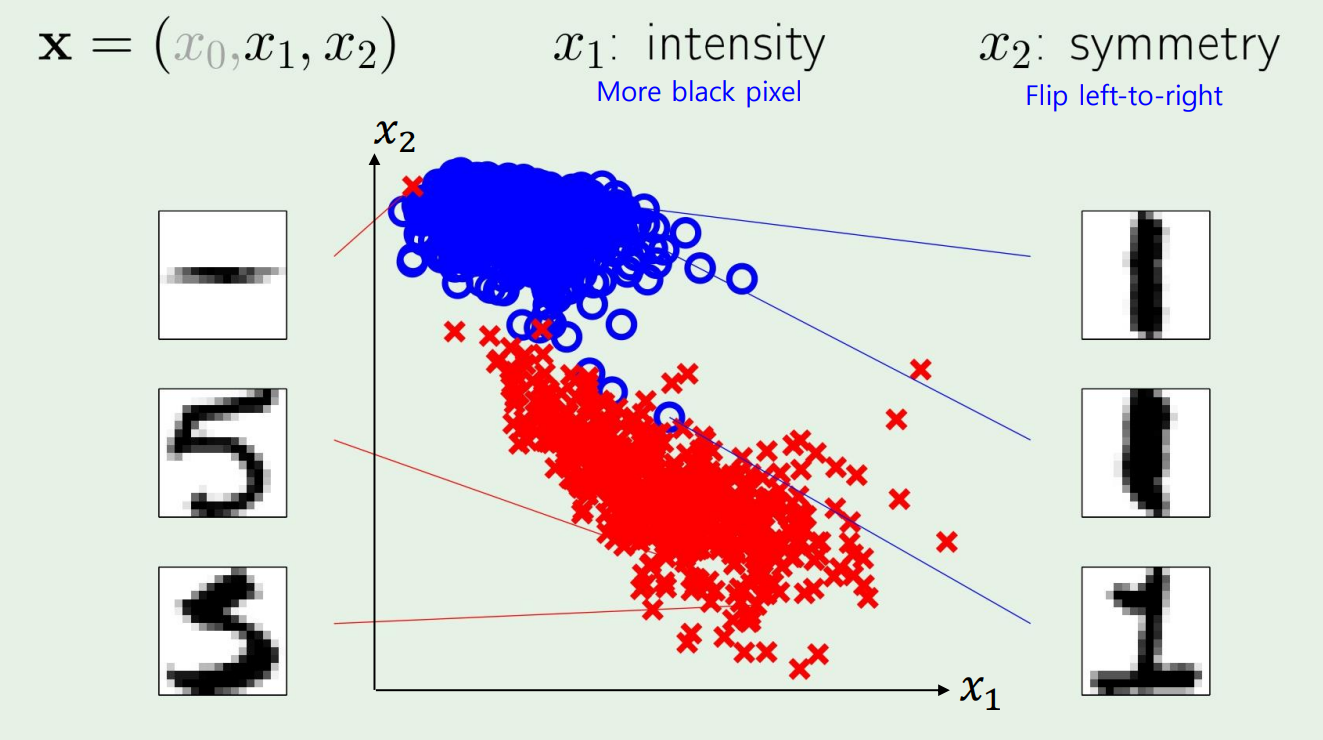
• intensity : how many black pixel? $\to x_1$
• symmeetry : 대칭성 $\to x_2$

그렇다면 $X = (x_0, x_1, x_2)$, linear model : $(w_0, w_1, w_2)$ 이다.

예시를 들자면, 1은 intensity가 낮고, 8은 intensity가 높다.
그리고 1은 perfectly symmetric하고, 5는 아니다.

PLA

Perceptron Learning Algorithm으로 문제를 풀어보자.

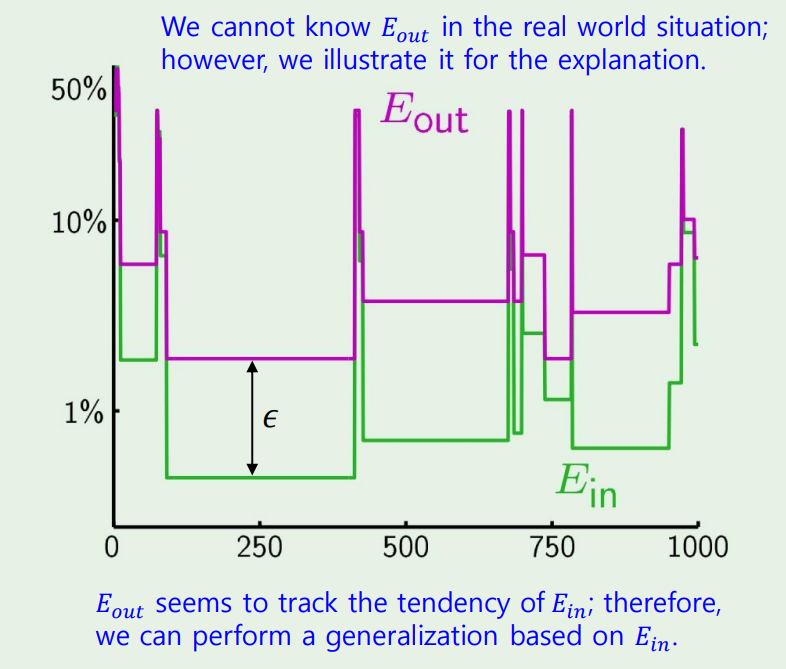
사실 우리는 $E_{out}$을 알수없지만, hoeffding에 의해 $\epsilon$만큼의 차이가 존재한다는것을 알고, 우리의 목표는 그 차이를 줄이는 것이다!

근데 이렇게만 하는것이 아닌, for loop가 돌아가는 동안, 새로운 hypothesis가 생길때마다 이전의 h와 비교하여 더 나은 h를 찾는 방법이 존재한다.

pocket

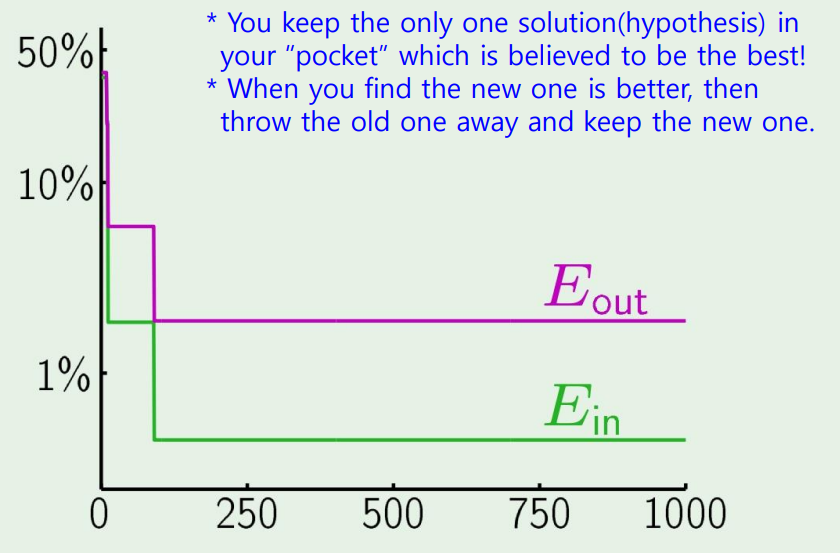
우리가 perceptron을 실행시킬때, 결국 weight를 업데이트 해가는데, 업데이트는 error를 보고, error에 대해 편미분을 한뒤 gradient를 가지고 업데이트 해간다.

근데 weight를 업데이트하기 전에, 새로운 gradient가 나온다면 그 gradient를 가지고 error를 한번 구해보고, weight를 업데이트하는게 error를 증가시키면 weight를 바꾸지 않고 기존을 유지하는 방식이다.

Classification boundary PLA VS Pocket

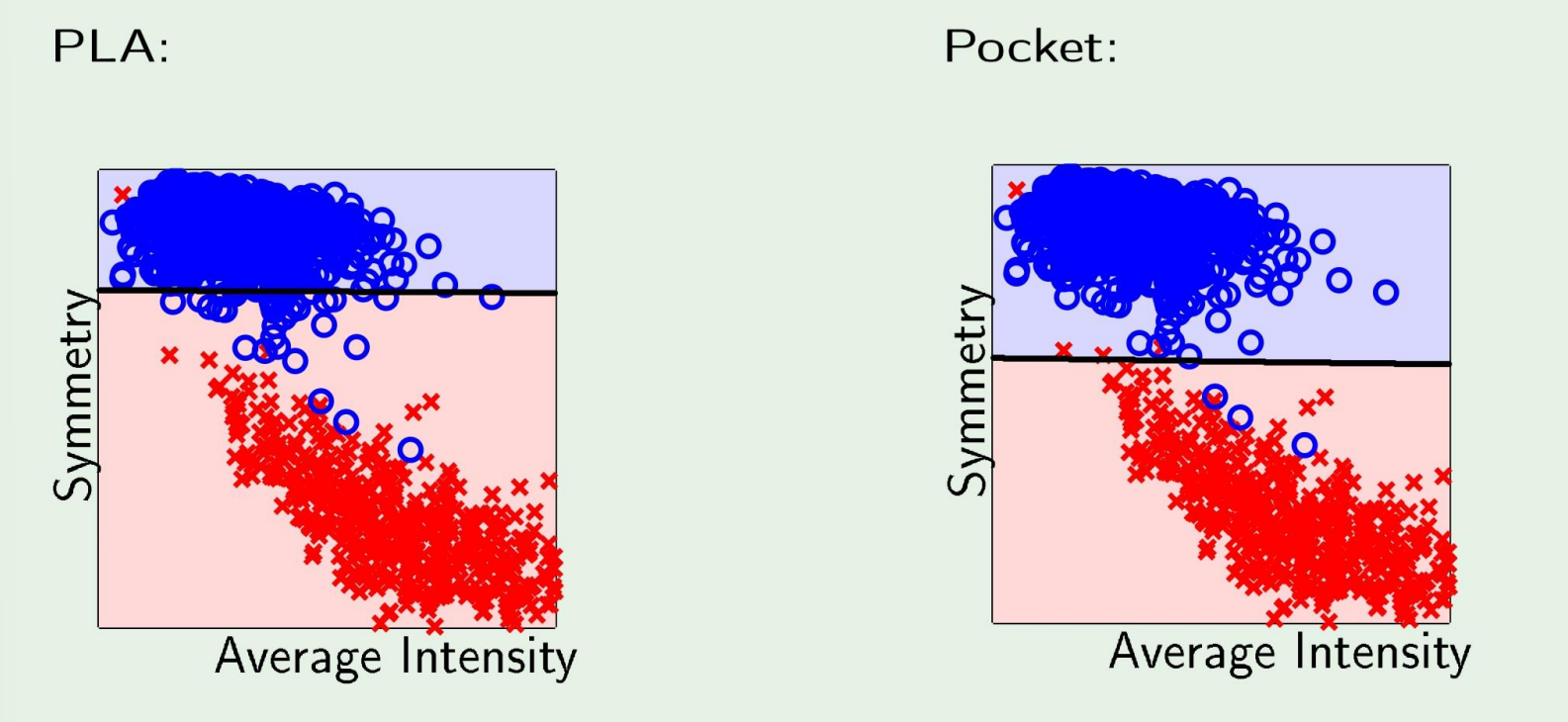
매번 새로운 weight마다 업데이트하는 PLA보다 pocket이 좀더 잘 분류하는것을 확인할 수 있다

---

그렇다면 Linear Regression, real-value는 어떻게 풀어야할까?

간단한 예시로 돈을 빌려주는 예시를 생각해보자.

그렇다면 classification은 돈을 빌려주는 관점에서 (yes/no)로 나뉘고,
regression은 credit line, 얼마나 빌려주어야 할지를 결정한다.

즉 real-value를 얻고싶은것이기 때문에,

이다.

그리고 여기서 우리는 이미 알고있듯이, in-sample error를 MSE로 놓으면 된다.

The expression for $E_{in}$

그리고 w는 다음처럼 쉽게 구할수있다.

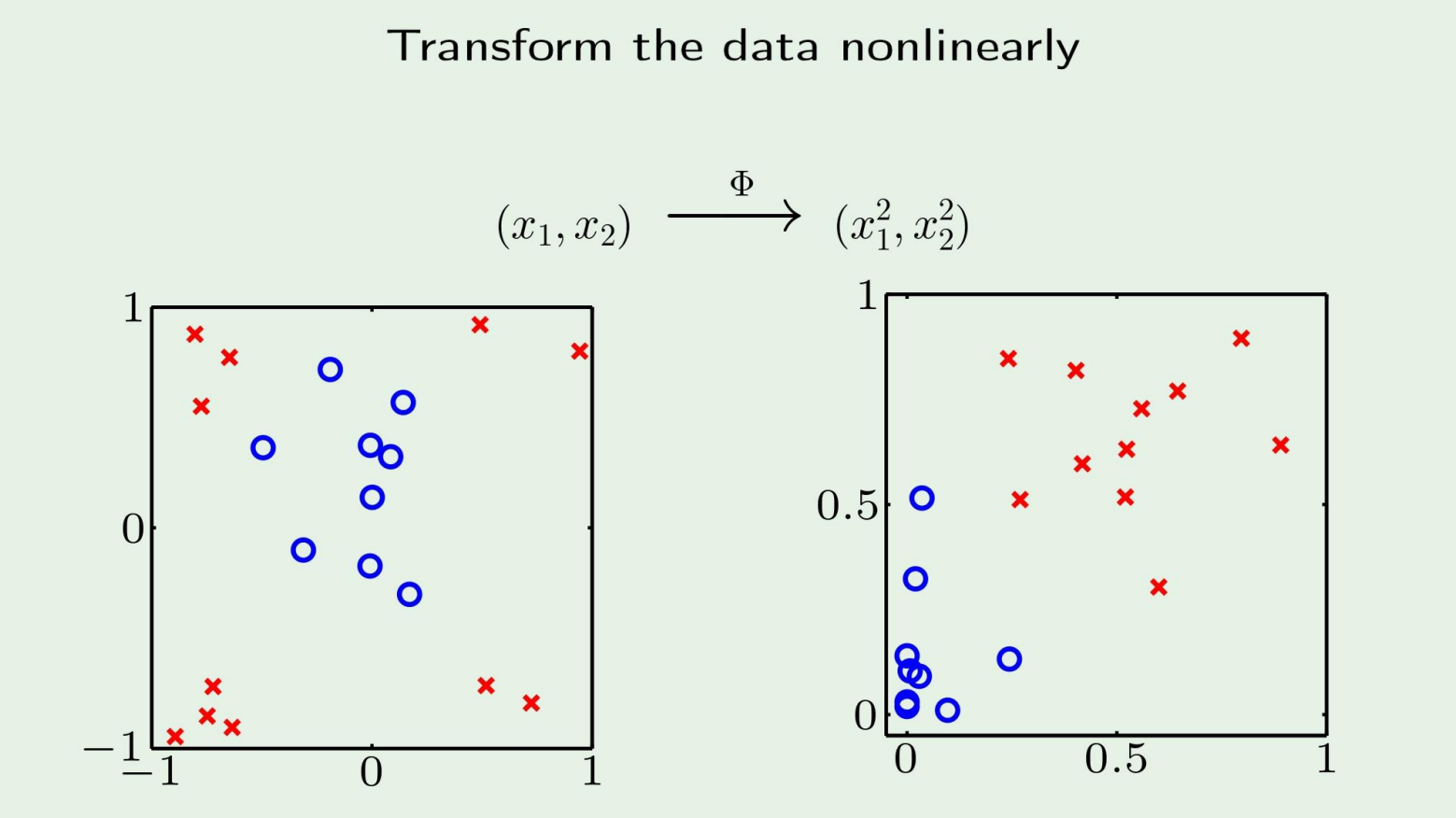
Nonlinear Transformation

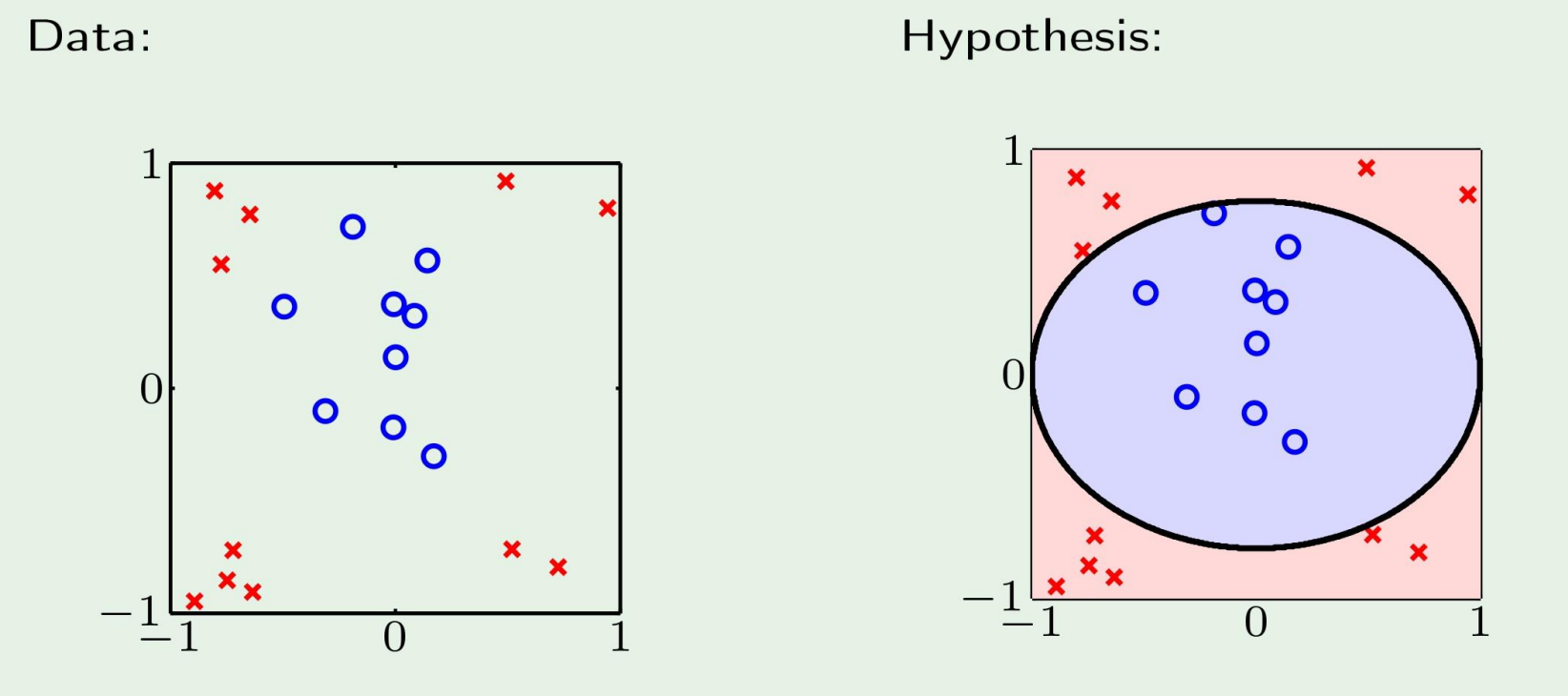
왼쪽과 같은 data가 주어졌을때 우리는 h를 오른쪽과 같이 만들면 된다는 것을 직관적으로 알수있다.
그러나 기계는 모른다.
그렇다면 어떻게 해야할까?

데이터들을 다른 공간으로 shift하면 된다! (나중에 나올 kernel method)

또다른 예시를 보자.

$[[x_i < 1]]$ return 1 if true, 0 otherwise
$[[x_i > 5]]$ return 1 if true, 0 otherwise

이런 logic 연산이 존재한다고 해보자. 이는 당연히 nonlinear하다.

근데 우리는 이걸 Linear model로 풀고싶은데 어떻게 해야할까?

Linear in what?

Linear regression implements

Linear classification implements

여기서 우리의 hypothesis를 결정하는것은 바로 ${\color{Red} \text{weight}}$이다.

왜 이게 linear하냐면, 나의 hypothesis는 $w_i$에 dependent함.
$w_i$의 관점에서 $x_i$는 단순히 constant이고, 결국 $w_i$를 내가 학습해야 하는것 이므로 $\to$ linear하다!